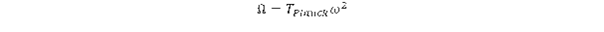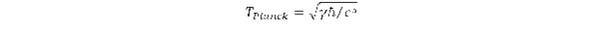A mérés hogyan változtatja meg a vizsgált rendszer állapotát?

Galilei számára, amikor távcsövével az éjszakai eget kémlelte, természetesnek tűnt, hogy evvel nem változtatja meg az égitestek mozgását. (Itt hagy hívjam fel a figyelmet Kolozsi Ákosnak az Index tudomány rovatában megjelent mértékadó cikkére: Akár az egyháznak is igaza lehetett 400 éve Galileivel szemben). .Ezért amikor kifejtette nézetét a fizikai törvények objektivitásáról nem kellett arra gondolnia, hogy befolyásolja-e a megfigyelés a megfigyelt rendszer állapotát. Felfogása szerint léteznek törvények, amelyek matematikai formába önthetők és ez feltárható és ellenőrizhető reprodukálható kísérletek által. A modern fizika, amikor a mikrovilág titkait kutatja alapvetően más helyzetben van, mert megváltoznak a nagyságrendek. A csillagászatban a parányi ember figyeli az óriások birodalmát, a mikrofizikában pedig a megfigyelő ember az óriás a megfigyelt mikroszkopikus objektumokhoz képest. Megváltozott a megfigyelés, a kísérletek jellege is, nem csupán felnagyítjuk a képet a szemünk számára közvetlenül már nem látható objektumokról mikroszkóppal, vagy hatalmas távcsövekkel, hanem egyre nagyobb elektromos és mágneses terekkel változtatjuk meg az elemi részecskék mozgását a gyorsítókban, nagyenergiájú sugárzással, vagy elemi részecskék bombázásával tárjuk fel az anyag szerkezetét. Tehát a megfigyelés már nem passzív tevékenység, hanem aktív beavatkozás a megfigyelt objektum állapotába. Közkeletű felfogás szerint az „ellenőrizhetetlen beavatkozás” vezet arra, hogy bizonyos tulajdonságok – például a pozíció és az impulzus – nem is mérhető meg egyidejűleg tetszőleges pontossággal, amelynek határát a kvantummechanika bizonytalansági elv szabja meg.

Hol a határ a megfigyelő és a megfigyelt objektum között?

Honnan származik a mikrovilágot uraló valószínűség, tényleg határozatlanok az elemi folyamatok, vagy csupán a róluk szerzett információnk bizonytalan? A kérdés kiindulópontja a határ megválasztása a megfigyelést végző ember és a megfigyelt világ között, vajon műszereink a megfigyelt világhoz tartoznak, vagy csupán kiterjesztett szemünk, érzékelési eszközünk, amivel megsokszorozzuk képességünket, hogy megismerjük a világot? És mi a szerepe a külvilágról szerzett információ hordozóinak, alapvetően a fénynek, a fény elemi részecskéinek, a fotonoknak? A világot a kölcsönhatásokon keresztül ismerjük meg, mégis a tudomány olyan törvényeket alkot, amiből kizárja a megfigyelőt, azaz „objektívnak” tekinti a törvényeket, amely független attól, hogy ki a megfigyelő. és attól sem függ, hogy milyen eszközökkel, műszerekkel jutottunk el az információhoz.

A kérdező és a megkérdezett viszonya

Nem csak a fizikában merül fel a kérdés, hogy maga a kölcsönhatás, a „kérdezés” megváltoztatja-e azt az állapotot, amit meg akar ismerni. Ha a közvélemény kutató megkérdez valakit bármiről a válaszoló önkéntelenül meg akar felelni bizonyos normáknak, mert nem akar „rossz színben feltűnni”. Jellemző erre a „győzteshez való igazodás”. Egy politikai választás után mindig többen mondják, hogy a győztesre szavaztak, mint ahányan ténylegesen az adott pártot támogatták. Hasonló helyzetben van a kutató is, ha valamilyen elméletet igazolni, vagy cáfolni akar. Ha a mérés ellenkezik a várakozásával, akkor gondosan ellenőrzi, hogy nem követett el valamilyen hibát a kísérlet során. Ha viszont a mérés megfelel a várakozásnak, akkor a kutató kevésbé lesz kritikus az eredménnyel. Ez időnként vezethet hibás megállapításokhoz, elméletekhez is, de nem akadályozza meg a helyes törvények megállapítását, mert más kutatók később korrigálhatják a tévedést.  A valóban lényeges kérdés ezért nem a kutató szubjektív viszonya az elért eredményekhez, hanem az, hogy a kölcsönhatás által megváltoztatott rendszer mennyiben tekinthető azonosnak a kölcsönhatás előtti állapotával.

Változás nélkül nincs megfigyelés

Ha egy mikro rendszerben, például egy atomban, vagy molekulában, az elektronok energiáját akarjuk megállapítani, akkor meg kell változtatni az elektron állapotát valamilyen frekvenciájú fénnyel besugározva, vagy észlelnünk kell azokat a fotonokat, amit az elektron kibocsát, miközben ugrást végez két állapot között. Ha nem következik be valamilyen változás az elektron állapotában, akkor nem is „látjuk” az elektronokat, azaz nincs róla semmilyen információnk. Emiatt nem a kísérletileg már meghatározott energiaállapotok alapján határozzuk meg, hogy milyen frekvenciájú fotonokat bocsát ki, vagy nyel el a rendszer, hanem fordítva: az ugrásokat látjuk, és ebből következtetünk arra, hogy mekkora lehetett az a két energiaszint, ami között létrejött az ugrás. Ezért alapvető a kölcsönhatást közvetítő foton szerepe, amelynek saját tulajdonságai határozzák meg, hogy milyen információt szerezhetünk az elektronok állapotáról. Viszont a foton „egydimenziós” részecske, ami alatt azt kell érteni, hogy egyetlen szabad paramétere van a ν  frekvencia, amely meghatározza az összes tulajdonságát: az energia E = hν, a hullámhossz λ = c/ν, az impulzus p = hν/c = h/λ. Minden foton rendelkezik egy közös tulajdonsággal, ugyanis az impulzusnyomatékuk I = ℏ = h/2π megegyezik. Annak is külön jelentősége van, hogy a hullámhossz és az impulzus szorzata a Planck-állandó: λ.p = h. Ezt azért emelem ki, mert bizonyos törvényeket nem a kvantummechanikából akarok származtatni, hanem megfordítom a logikai következtetések irányát, nevezetesen plauzibilis fizikai elvekből kiindulva értelmezem a mikrovilág törvényeit. Evvel az a célom, hogy összhangot találjak a kvantumfizika szokatlan jelenségei és a józanész között.

A foton mint postás

Példaképp vizsgáljuk meg valamilyen anyag szerkezetét nagyteljesítményű mikroszkóppal. Akármilyen összetett lencserendszert is használunk, van egy határ, amit nem tudunk átlépni, ha látható fényt használunk. Ez a határ a fény hullámhossza, ami nem sokkal 1 μm (10^-6m) alatt van. Ennek oka, hogy a fény hullámhossza adja meg azt a periódushosszat, amivel a fényhullámok sora ismétlődik. Ezt úgy foghatjuk fel, mint egy mérőrudat, aminek skálabeosztását λ adja meg. Ha egy molekula szerkezetét akarjuk látni, akkor finomabban skálázott méterrúdra van szükség. Használjunk ezért Röntgen-sugarakat, ahol a beosztás már 0,1 nm (10^-10 m) és sugározzunk be egy egykristályt, amelyben minden molekula szabályos rendben helyezkedik el. A sugárzás eredeti irányához képest ekkor különböző szögekben figyelhetünk meg diffrakciós foltokat és tanulmányozhatjuk ezek pozícióját miközben forgatjuk a kristályt. Ebből már megfelelő matematikai eljárások útján meghatározhatjuk a molekula szerkezetét. A távolságmérés pontossága rövidebb hullámhosszú sugárzás alkalmazásával fokozható. Viszont a foton λ hullámhosszához p = h/λ impulzus tartozik, amellyel a sugárzás meglöki a vizsgált fizikai objektumot, és ennek mértékében megváltozik az objektum eredeti impulzusa. Ha most egy újabb mérést végzünk az impulzus meghatározására, akkor függetlenül az új mérés pontosságától, az eredeti impulzust már nem tudhatjuk pontosabban, mint amivel az első mérés fotonja rendelkezett, hiszen ekkor már a megváltozott állapotú rendszeren végezzük el a mérést. A két mérésből tehát azt kapjuk, hogy a vizsgált objektum pozíciójának és impulzusának mérési hibáját szorozva a h Planck-állandó adódik ki. Végső soron az információ közvetítőjének, a fotonnak tulajdonságából következik, hogy a pozícióról és az impulzusról nyerhető ismeretünk korlátozott pontosságú lesz. Ennek felel meg a kvantummechanika szabályaiból levonható következtetés, amit a Heisenberg-féle bizonytalansági relációnak nevezünk. (A matematikai levezetést lásd: A kvantumvilág rejtélyei 3.) A kvantummechanika tehát egy olyan matematikai formalizmus, amely magában hordja a foton alapvető tulajdonságait és emiatt lesz a részecskéről szerezhető információ pontossága korlátozott, azaz nem következik a bizonytalansági relációkból, hogy a részecske pozíciója és impulzusa lenne határozatlan .

Hogyan tükrözi a kvantummechanika a foton tulajdonságait?

Minek köszönhető, hogy a kvantummechanikai formalizmus összhangban van a foton szerkezetéből fakadó információs határozatlansággal? Ennek oka a fizikai mennyiségek operátorainak definíciójában rejlik. A fizikai mennyiségek hatásuk alapján definiálhatóak, az energia az a mennyiség, ami nem változik időben a mozgás során, az impulzus pedig a térben nem változik, ha a mozgás sebessége állandó (ez a Noether-elv). Az időbeli változást matematikailag a δ/δt, a térbeli változást a δ/δx, δ/δy, δ/δz differenciálhányadosok írják le. Foton esetén az időt „kvantálja” a hullám 2π fázisismétlődési ideje, a T =1/(2πν) = 1/ω periódus idő, ezért a δ/δt differenciálhányadosnak 1/T = ω felel meg. Viszont az energia E = ℏω, ahol ℏ = h/2π a redukált Planck-állandó, ezért ez fog szerepelni az operátorokban is. Emiatt definiálja a ℏi δ/δt operátor az energiát és  ℏ/i δ/δx, ℏ/i δ/δy, ℏ/i δ/δz az impulzus komponenseit. (Az i imaginárius egység megjelenésének okát lásd: Út a kvantummechanika megértéséhez.)

A kvantumelektrodinamika szemléletmódja

A kvantummechanika eredeti formája, amit Schrödinger és Heisenberg alkotott meg, még magán viseli a klasszikus fizika szemléletmódját, mert a mikrorendszer részecskéit még önmagában vizsgálja és a fotonokat az észlelő rendszer részének tekinti. Ezt a határt változtatja meg a mezőelmélet, amikor az elektrodinamikának kvantumos leírást ad a kvantumelektrodinamika (QED) elméletében. Ez az elmélet már egyenrangú és elválaszthatatlan szerepet ad az elektronoknak és a fotonoknak, mindkét részecskét oszcillátorok írják le, amelyek képződnek és eltűnnek a mikro folyamatokban. Például, amikor az atom elektronja az egyik állapotból átugrik egy másik állapotba, akkor ez elektron eredeti állapotát leíró oszcilláció eltűnik (annihiláció), de létrejön egy új állapotú elektron oszcilláció, valamint egy fotont leíró oszcilláció is. Az annihilációt és részecske képződést operátorok írják le és az operátorok sajátértékének a fotonok és elektronok száma felel meg. Ezt az eljárást nevezik második kvantálásnak.

 A QED elmélete tehát eltolja a határt a mikro folyamatok és a megfigyelő között, amikor az információt hozó fotonokat is a megfigyelt objektum részéve teszi. A határozatlansági reláció azonban továbbra is érvényben marad, bár ekkor a fotonkibocsátás hatását az elektronok állapotára (például az impulzus változását) az elmélet számításba veszi. Ennek oka, hogy az elektronok és fotonok viselkedése nem választható szét, és az összefonódás mértékét a bizonytalansági reláció szabja meg. Az elmélet arra is vállalkozik, hogy leírja a töltött objektumok közötti elektromágneses kölcsönhatást. Például az elektron és a proton azért vonzza egymást, mert állandóan virtuális fotonok seregét bocsátják ki és nyelik el. Ezek a kölcsönhatást közvetítő fotonok nem figyelhetők meg (ezért virtuálisak), szerepük az elektromágneses mező felépítése és fenntartása. Ezek nem számunkra hozzák az információt, hanem az elektromosan töltött részecskékhez szólnak, ezek a részecskék ily módon hatnak egymásra és „észlelik” egymás távolságát, mozgását. Az állandóan képződő és eltűnő virtuális fotonok a sztatikus elektromos és mágneses mező helyett ingadozásokat hoznak létre (ezt hívják vákuumingadozásnak illetve polarizációnak). Átlagértékben meghatározzák például a Coulomb-potenciált, de az ingadozás kismértékű többlethatást is okoz, amely megjelenik az elektron anomális mágneses momentumában és a Lamb-shiftben is (lásd az ide vonatkozó bejegyzést).

A virtuális fotonok világa

Ebben a képben az elektron „több önmagánál”, mert elválaszthatatlanul hozzá tartozik a virtuális fotonok serege, a töltése által keltett elektromágneses mező. Hasonlóan a foton sem csupán „önmaga”. Az elektron-pozitron pár annihilál és fotont bocsát ki, fordítva pedig a foton hozhat létre elektron-pozitron párokat. Ezek is virtuálisan jelen vannak az elektromágneses mezőben, ezek is részét képezik a fotonoknak. Ennek a furcsa világnak a tulajdonságát írja le Feynman diagramjaival és beszámol különleges tulajdonságairól könyvében: „QED: The Strange Theory of Light and Matter”, Princeton University Press, 1985. A különös tulajdonságok közé tartozik, hogy a hatások lokálisan átléphetik a fénysebességet, sőt még az oksági elvnek sem engedelmeskednek, mert egy elektron-pozitron pár előbb fejtheti ki hatását, mint ahogy létrejön.

Segíthet a józanész a kvantummechanika megértésében?

Annak érdekében, hogy a QED elmélet furcsaságait közelebb hozzuk a józanészhez, lépjünk vissza az időben, amikor még a kvantumelmélet csak születőben volt. Az első atommodellt Bohr alkotta meg. A klasszikus elektrodinamikát vette alapul és úgy képzelte el az elektronok mozgását az atommag körül, mint ahogy a bolygók keringenek a Nap körül. A problémát az jelentette, hogy minden gyorsulást végző töltés (a keringő mozgás is gyorsulás az állandó irányváltoztatás miatt) fényt, azaz fotonokat bocsát ki. Ez viszont állandó energiaveszteséggel jár, ezért az elektron nem lehetne stabil pályán az atommag körül. Bohr azonban bátor gondolkozó volt és feltételezte, hogy mégiscsak léteznek olyan pályák, ahol nincs fénykibocsátás, amit ő stacionárius pályáknak nevezett el. Később a kvantummechanika részben korrigálta elméletét (lásd erről részletesen a „Miért diszkrétek az energianívók kötött állapotban” című ötrészes bejegyzést), de a stacionárius pálya elvét megtartotta, amit az energia sajátfüggvényei képviselnek. A QED mezőelmélet ezen is tovább lépett, amikor a Maxwell-egyenletekből adódó foton kibocsátási szabályt beépítette oly módon, hogy ezek virtuális fotonok, amelyek nem figyelhetők meg és nem változtatják meg az elektron állapotát, mert a stacionárius pályán mozgó elektron egyidejűleg bocsátja ki és nyeli el a fotonokat.

A mikrorendszerek irány fogalma

Össze lehet-e egyeztetni ezt a furcsa képet a józanésszel? Próbáljuk meg! Hétköznapi világunkban minden pillanatban óriási mennyiségű információ ér minket, a fotonok garmadája jut el a szemünkbe, amit feldolgoz az agyunk. Összehasonlítja a különböző helyekről érkező fotonokat és megalkotja az irány fogalmát. De mit tenne akkor agyunk, ha csak egyetlen irányból jutna el szemünkbe a fény? Lenne akkor értelme az iránynak? Nyilván nem. Az elektron is hasonló helyzetben van, amikor az atommag körüli pályán tartózkodik, ekkor csak a centrumtól való távolságot „érzékeli”, ezért számára az irány fogalma értelmetlen. Mi azonban a makrovilágból nyert fogalmaink alapján képzeljük el az elektron mozgását, ezért matematikai leírásunkban a szokásos háromdimenziós teret vesszük alapul. De a mikrovilágban, ha egy atomról van szó, az irány már fiktív! Mit várhatunk ekkor az irányváltás miatt kibocsátott fotonoktól? Ezek is fiktívek lesznek! Ha nincs valódi irány, akkor a pálya ellentétes pontjain kibocsátott fotonok egymást kompenzálják, azaz képződnek és azonnal elnyelődnek. Így juthatunk el a QED virtuális fotonjainak koncepciójához! Abban a világban, ahol nincsenek egymást követő események az idő fogalma is elvész. A stacionárius pályán lévő elektron számára is ez a helyzet, hiszen csak az számít „eseménynek”, amikor két állapot között ugrást végez, és emiatt a kölcsönhatási folyamataiban nincsenek olyan események, melyeket idősorrendbe lehetne állítani. Így az idő is fiktívvé válik, és ez mutatkozik meg a QED elméletben számításba vett kölcsönhatásokban is. A mikrovilágnak ezt a sajátságát szemléltetem „Az intelligens elektron” című írásban is.

A foton a mikrorendszerek szabályozója: hogyan landol az elektron az atomban?

A foton nem csak a mikrorendszerek postása, hanem szabályozója is. A kötött állapotok energiaugrásai a foton kvantumos természetéből következnek, amit két példán mutatok be: a hidrogén atomban és a vegyérték rezgések esetében. A kvantummechanikai leírás – összevetve a klasszikus fizika módszertanával – olvasható a „Miért diszkrétek az energiaállapotok kötött állapotban” című bejegyzésben. Itt most az elvi alapokat foglalom össze. Hogyan jön létre a hidrogén atom egy távoli protonból és elektronból? Ha a két részecske mozgása során elég közel kerül egymáshoz, akkor a közöttük lévő elektromos vonzás gyorsítani fogja a részecskéket. A gyorsulás fotonok kibocsátásával jár. Ezt nevezi a szakirodalom fékezési sugárzásnak, ami például a ciklotronban is fellép és jelentős energiaveszteséget okoz. A fékezési sugárzás szerepe hasonló a fékező rakétához, amelyik elősegíti a „landolást” és a kötött pálya kialakulását. A gyorsulás beindulása előtt az elektron mozgása nem hoz létre pálya-impulzusnyomatékot, viszont az elektron rendelkezik saját impulzusnyomatékkal, spinnel, aminek értéke ½ℏ. Minden fotonkibocsátás ℏ impulzusnyomatékot igényel, ennek forrása az S = ½ spin, mert a spinnek két lehetséges állapota van, melyek nyomatékkülönbsége éppen ℏ. Az elektron közeledve a protonhoz, ha pályája nem pontosan a protonhoz tart, akkor pálya-impulzusnyomatékra tesz szert, amely a kibocsátott és elnyelt fotonoktól származik. Emiatt viszont a pálya-impulzusnyomaték mindig ℏ egységekben változik és így az atomi pályán tartózkodó elektronok kizárólag ℏ egészszámú többszörösének megfelelő impulzusnyomatékkal rendelkezhetnek. A kvantumosan változó impulzusnyomaték viszont diszkrét energiaállapotokkal jár együtt. Ezt írja le a kvantummechanika is. A diszkrét energia nívók azonban csak a kötött állapotra jellemzők, de ha az elektron „szabad”, akkor folytonosan változhat energiája, mert nem érvényesül a fotonok „szabályozó” szerepe. Ezt írja le a kvantummechanika, amikor megengedi, hogy az energiának ne csak diszkrét, hanem folytonosan változó sajátértékei is lehessenek.

Fotonok energiaadagolása molekularezgésekben

A molekulák atomjai rezgéseket végeznek a kötéshossz periodikus változásával, ezt a jelenséget vizsgálja az infravörös spektroszkópia. Az egyensúlyi helyzet kötéshosszának változása a megnyúlás, vagy a rövidülés mértékével arányos erőt hoz létre, amit Hook-törvénynek nevezünk. Az erőállandó és a rezgő tömeg hányadosa határozza meg a rezgési frekvenciát. A klasszikus leírásban a rezgési energia a kitérési amplitúdó négyzetével arányos és folytonosan változik. Ezzel szemben a kvantummechanikai leírás diszkrét és ekvidisztans közökben változó energiaszinteket határoz meg, ahol az egyes ugrások értéke h.ν, ahol ν  felel meg a rezgési frekvenciának. Ez a kép is értelmezhető a fotonok „szabályozó” szerepével. A fotonok ugyanis csak akkor emelhetik meg, vagy csökkenthetik a rezgési energiát, ha frekvenciájuk pontosan megegyezik a rezgési frekvenciával. Viszont az ennek megfelelő foton energia éppen h.ν  és így a rezgő rendszer energiája is csak ennyivel változhat meg, ha fotont bocsát ki, vagy nyel el. Érdemes azon is gondolkozni, hogy az alapállapot miért nem nullaenergiájú, hanem ½hν? Ezt nevezik nullponti energiának, mert a molekularezgések még az abszolút zérus hőmérsékleten sem állnak le. A kvantummechanikai magyarázat a bizonytalansági reláción alapul: ha leállna a rezgés, akkor a kötött atom pozíciója teljes pontossággal lenne meghatározó, de ekkor az impulzus – és vele együtt az energia – ingadozása végtelenül nagy lenne, ami felszakítaná a kötést. De magyarázhatjuk a nullponti rezgést a fotonok szabályozó szerepével is, ami a fotonok és a kötött atomok rezgése közötti rezonanciával függ össze. A rezonancia ugyanis megköveteli, hogy a foton rezgési fázisa igazodjon az atom rezgési fázisához, márpedig mozdulatlan kötéshossz esetén nem jöhet létre rezonancia.

Egy szemléletes hasonlat

Szemléltessük a fotonok szabályozó szerepét egy hasonlattal. Töltsünk fel egy hordót vízzel. A víz szintje tetszőleges lehet a hordóban, ha folytonos vízsugárral töltjük fel. Ha viszont a vizet vödrökkel adagoljuk és mindig tele van a vödör, akkor a hordóban diszkrét szintek alakulnak ki. A foton is ilyen teli vödör, amelyik ℏ Planck-állandónyi impulzusnyomatékot, vagy hν energiát ad át az atomnak, illetve rezgést végző molekulának.

Ellenpélda a nem-kvantumos kölcsönhatásra

A foton közvetíti az elektromágneses kölcsönhatást, de mi közvetíti a gravitációt? Ez a kérdés a modern fizika neuralgikus pontja, amire mindmáig nincs érvényes magyarázat, persze akkor, ha nem a tér Einstein által feltételezett görbületére akarjuk visszavezetni, hanem valamilyen közvetítő részecskére, amit gravitonnak nevezett el a szakirodalom.

Lehetséges-e oszcilláció gravitációs mezőben?

 Létrehozhat-e a gravitáció olyan oszcillációt, mint a vegyértékrezgések? Elvben igen! Képzeljük el, hogy átfúrjuk a Földet és a lyukba leejtünk egy követ. A kő először a földfelszíni nehézségi gyorsulással indul meg, majd közeledve a bolygó centruma felé a ráható gyorsító erő csökkenni kezd, nulla lesz a centrumban, majd tovább repülve a mozgást már lassítani fogja a gravitáció. Ha nincs közegellenállás, vagy egyéb energiaveszteség, akkor a kő a Föld túloldaláig repül, ott megáll és elkezd visszafelé zuhanni. Ha nincs veszteség, akkor létrejön egy oszcilláció, akárcsak a vegyérték rezgések esetén. Csak annyi az eltérés a Hooke törvényhez képest, hogy a kőre ható gravitáció nem pontosan lineáris a centrumtól való távolsággal. Elvben a Hook törvény szerinti erőtörvény is kialakulhat, ha a gömb alakú Föld helyett egy kockára, vagy hengerre gondolunk, amit a szimmetriatengely mentén fúrunk ki. Ebben az esetben az erőtörvény pontosan megegyezik avval, ami a molekulában fellép a kötéshossz megváltozásakor. Ez az oszcillációs mozgás a bolygómozgás ellipszis pályájának felel meg, amelynek ellipticitása (lapultsága) végtelen.

Klasszikus vagy kvantumleírás kell az oszcilláció leírásánál?

Mivel makroszkopikus rendszert vizsgálunk, így használhatjuk a klasszikus Newton egyenletet, és az eredmény azonos lesz a rugó rezgését leíró egyenletekkel (Lásd „Miért diszkrétek az energiaállapotok kötött állapotban?”) De milyen leírást válasszunk, ha nem egy követ, hanem egy neutront, vagy egy Hidrogén atomot ejtünk le, akkor is a klasszikus mechanika törvényeit kell alkalmazni, vagy át kell térni a kvantummechanikára? Itt fontos, hogy a leejtett mikor-objektumnak ne legyen töltése, mert akkor a gyorsulás foton kibocsátással és energia veszteséggel jár, ahogy az elektron is sugárzást bocsát ki, amikor felgyorsítjuk a ciklotronban. Ha egy töltéssel nem rendelkező elemi objektum mozgását vizsgáljuk használhatjuk-e a Schrödiger egyenletet? Ha igen, akkor a vegyértékrezgéshez hasonló kvantált energiaállapotokat kapunk! Most készítsünk nagyszámú neutronból, vagy Hidrogénatomból egy makroszkopikus testet, ekkor, ha leejtjük ez is kvantált pályán fog mozogni? A válasz nem, mert ekkor a töltések hiányában két rezgésállapot között nem jön létre foton kibocsátás. Más szóval a mikrorészecske mozgása is klasszikus mechanika törvényeit fogja követni.

Az elektromágneses és a gravitációs potenciál viszonya

Az alapvető különbség a vegyértékrezgések és a gravitációs térben bekövetkező oszcilláció között, hogy a molekulában az egyes atomokat az elektronok elektromágneses kölcsönhatása köti össze, amelyben a virtuális fotonok hatása nyilvánul meg. Ha a gravitációnak valóban lenne kölcsönhatási bozonja, akkor elképzelhető lenne, hogy az oszcilláció tényleg kvantált legyen, de ekkor az egyes nívók energiáját már nem a h Planck állandó határozná meg, hanem egy gravitációs kvantumállandó.

A blog további írásairól ad tájékoztatót a „Paradigmaváltás a fizikában” című bejegyzés.

A Standard Modell részecskéi

A jelenlegi fizika a Standard Modellben összegzi az elemi részecskék tulajdonságait. Összesen már néhány száz részecskéről van szó, ha ebbe beleszámítjuk a tényleges elemi részecskék mellett a két illetve három kvarkból felépülő eleminek mondott, de valójában összetett részecskéket is, amit összefoglaló néven hadronoknak nevezünk. Ezen belül lehet megkülönböztetni a két kvarkból (pontosabban egy kvarkbók és antikvarkból) álló mezonokat és a három kvarkból, vagy antikvarkból álló barionokat.

Valódi elemi részecskék

Kezdjük először a valódi elemi részecskékkel. A leírásban a Standard Modell elnevezéseit és osztályozási elveit követem, de kiegészítem az egyes részecske típusok mozgásformáival, ami által jobban megérthetjük az alkalmazott osztályozási elveket is. Két alaptípust különböztetünk meg, az egyiket fizikai világunk „építőköveinek” tekinthetjük, ezek a fermionok, a másikat pedig mint az építőkövek közötti kölcsönhatások létrehozóit, illetve átalakítót képzeljük el, ez utóbbiak a kölcsönhatási bozonok. A közös tulajdonság, amiben megegyeznek, hogy minden valódi elemi részecskének van spinje, azaz saját impulzusnyomatéka, mégpedig a fermionoké S = ½, míg a bozonoké S = 1. A részecskék impulzusnyomatéka az S spin és a kvantum alapját képező ℏ redukált Planck állandó szorzata, azaz S.ℏ.

A részecskék saját impulzusnyomatékának eredete

 Ahogy azt a blog különböző bejegyzésében többször kifejtettem, úgy értelmezem a részecskék saját impulzusnyomatékát, mint a téridő fénysebességű forgását, még pedig bozonoknál egytengelyű, fermionoknál két tengely körüli forgásokat tételezek fel. (Lásd:  „A tér szerkezete és az elemi részecskék mint rezonanciák”. Az előbbi forgás egy körpályát, az utóbbi gömbpályát hoz létre, ahol az utóbbit úgy képzelhetjük el, hogy az első tengely körüli körpálya forgást végez az átmérője körül. Ekkor a forgások egymáshoz képesti viszonya kétféle lehet: jobb- és balsodrású, ami a háromdimenziós tér egyik alapszimmetriájának, a kiralitásnak felel meg. A kétféle kiralitás hozza létre a részecske-antirészecske kettőséget a részecskék világában. A kettős forgás egyúttal magyarázza, hogy miért fele akkora a fermionok spinje a bozonokhoz képest.

Kölcsönhatási bozonok: egytengelyű forgások

Az egytengelyű forgások közé tartoznak az elektromágneses kölcsönhatás közvetítői a fotonok és a gyenge kölcsönhatás W+, W- és Z bozonjai. A foton nem rendelkezik sem nyugalmi tömeggel, sem töltéssel, szemben a W bozonokkal, amelyik mindkettővel rendelkezik, ráadásul a tömege igen nagy, közel százszorosa a nukleonokénak (proton és neutron). A Z bozon tömege meghaladja a W bozonokét, de töltés semleges. A fotonokat és a gyenge kölcsönhatás bozonjait az elektro-gyenge kölcsönhatás mezőelmélete kapcsolja össze. A négy részecske közös eredete úgy értelmezhető, hogy mindegyiknél a körmozgáshoz kapcsolódik még egy fénysebességű haladó (transzlációs) mozgás is. Foton esetén a transzláció iránya párhuzamos a forgástengellyel, míg a W és Z bozonoknál arra merőleges. Ebből adódnak a részecskék eltérő tulajdonságai. Mivel a fénysebességű mozgás a speciális relativitáselmélet szerint végtelen nagyra növelné a nyugalmi tömeget, ezért a foton nem rendelkezhet nyugalmi tömeggel.

Ekvivalencia elvek a részecske fizikában

A kvantumelektrodinamika alapfeltevése, hogy az elektromágneses kölcsönhatást a fotonok (virtuális és valódi) közvetítik, ezt az elvet oly módon lehet párhuzamba vonni a gravitációval, hogy ekvivalencia elveket vezetünk be. Ezek az ekvivalencia elvek különböző tehetetlenségi erőkhöz kapcsolják az egyes kölcsönhatásokat. Az einsteini általános relativitáselmélet kiinduló pontja, hogy a gyorsuláskor fellépő tehetetlenségi erő és a tömegvonzás ekvivalens, ennek mintájára tételezzük fel, hogy az elektromágneses kölcsönhatásban a forgó rendszeren belül mozgó testre ható Coriolis erő a kölcsönhatás forrása. Mivel a forgás tengelyirányában a Coriolis erő nulla, így a fotonnak nincs elektromos töltése (a nulla töltés fejezi ki, hogy nincs elektromos kölcsönhatás), szemben a W bozonokkal, ahol ez az erő létezik. A forgástengelyre merőleges elmozdulás azonban lehet jobb- és balsodrású, ezért jön létre a pozitív töltésű W+ és a negatív töltésű W- bozon. A Z bozon egy kvantummechanikai szuperpozíciós állapot, ahol a kétféle transzláció azonos súllyal szerepel, és emiatt a töltés megszűnik, akárcsak a későbbiekben tárgyalandót neutrínók esetében.

A foton fizikai paraméterei

A foton tulajdonságait az ω körfrekvencia határozza meg, nevezetesen energiája ℏ.ω, ez viszont a relativitáselmélet tömeg-energia ekvivalencia elve – azaz E = m.c² szerint – azt jelenti, hogy a foton rendelkezik mozgási tömeggel: m = ℏ.ω/c². Ez úgy értelmezhető, hogy a téridő kétféle fénysebességű mozgása alkotja meg a foton tömegét a nulla nyugalmi tömegből. A foton ω frekvenciáját a fénysebességű forgás frekvenciájával azonosítva kapjuk meg a forgás sugarát r = c/ω, amit az m.c impulzussal szorozva kapjuk meg az impulzus nyomatékot:  I = m.c.r = ℏ, azaz a foton spin tényleg S = 1! Az m tömegű ω frekvenciával forgó testre hat az F_cf = m. ω²r = m.c²/r = ℏ.c/r² centrifugális erő. Ezt pontosan ellensúlyozza a fénysebességű forgásoknak megfelelő extrém téridő görbületéből származó erős gravitáció. Az extrém görbületet az okozza, hogy a Lorentz kontrakció miatt a kör kerülete nullára zsugorodik. (Lásd „Fénysebességű forgások és a relativitáselmélet” és „Térgörbület és gravitáció forgó rendszerekben”).

Gyenge kölcsönhatási bozonok

A gyönge kölcsönhatás W és Z bozonjai esetén a forgástengelyre merőleges transzláció a sugár fénysebességű növekedését okozza, viszont az ω = c/r szabály miatt csökkenti a frekvenciát és evvel együtt a részecske energiáját és tömegét. Természetesen ekkor is a tömeg valójában mozgási tömeg, de ez a tömeg nagyon rövid idő alatt eltűnik és emiatt a részecskék által közvetített kölcsönhatás hatótávolsága nagyon rövid lesz, ami összhangban van a gyenge kölcsönhatás ismert tulajdonságaival. Ugyanakkor a kölcsönhatási bozon frekvenciaváltoztatási képessége teszi lehetővé, hogy a különböző sajátfrekvenciájú fermionokat egymásba alakítsa. Amikor viszont változik a forgás frekvenciája fellép egy újabb tehetetlenségi erő, amit Euler erőnek nevezünk. Lásd: „Az elektro-gyenge kölcsönhatás és az elemi részecskék átalakulása”., "A gyenge kölcsönhatás kiválasztási szabályai és a CPT tükrözés"

Ekvivalencia elvek és fizikai erők

 Kiterjeszthetjük az ekvivalencia elvet az Euler erő és a gyenge kölcsönhatás ereje között is. Végeredményben tehát három féle tehetetlenségi erő ekvivalenciája vezet el három kölcsönhatáshoz:

• a centrifugális erő felel meg a részecske forgását biztosító erős gravitációnak,
• a Coriolis erő felel meg az elektromágneses erőnek,
• az Euler erő felel meg a gyenge kölcsönhatásnak.

Nem volt még szó az erős kölcsönhatást közvetítő gluonokról, ezt majd a kvarkokkal kapcsolatban tárgyalom.

Az elemi fermionok mozgásai

A valóban eleminek tekinthető részecskék másik típusát képviselik a fermionok, amit a kéttengelyű fénysebességű forgásokkal lehet jellemezni. A két forgás megduplázza a centrifugális erőt, amiért a téridő görbülete csak fele akkora impulzusnyomatékot hoz létre. Innen származik az S = ½ spin. A Standard Modell megkülönbözteti az elektront, pozitront, a neutrínót és a kvarkokat. A kvarkoknak két alaptípusa van, amelyek a töltésükben különböznek: „up” töltése ±2/3e és „down” töltése ±1/3e. Minden részecske típusnak három generációja van, az elektron esetén a müon és tauon. A magasabb generációknak a tömege jóval nagyobb, de a töltésük megegyezik az alaptípussal.

Az elektron és pozitron esetén a kettősforgás tiszta jobb- vagy balsodrású kiralitással rendelkezik, ezért töltésük negatív illetve pozitív elemi töltés. A müon és tauon abban különbözik az elektrontól, hogy nagyságrendekkel nagyobb forgási frekvenciájuk és ennek megfelelően nyugalmi tömegük. A neutrínó esetén a kétféle kiralitás egyenlő súllyal van jelen, ezért nincs elektromos töltése. „A Dirac egyenlettől az általános fermion egyenletig” című bejegyzésben kimutattam, hogy neutrínó esetén a töltés megszűnésével együtt a tömeg várható értéke is nulla lesz, ugyanakkor a részecskének jól definiált impulzusa van. A nulla nyugalmi tömeg teszi lehetővé (sőt kívánja meg), hogy a fotonhoz hasonlóan fénysebességgel mozogjanak. A neutrínó oszcilláció jelensége szerint három különböző neutrínó létezik, de ezeket nem nyugalmi tömegük különböztetik meg, hanem az impulzusuk. Lásd még: „A tömeg és töltés kettős arculata”

Miért nincs szabad kvark?

Kvarkok esetén a tört töltést az okozza, hogy a két királis forgás eltérő súllyal szerepel a szuperponált kettős forgásban. A kvantummechanikai felfogásban ez azt jelenti, hogy a részecskék nincsenek se töltés, se tömeg és se impulzus sajátállapotban (Lásd: „A Dirac egyenlettől az általános fermion egyenletig”). Ezért lehet csak „renormált” és nem valódi tömegekről beszélni kvarkok esetén. Egy részecske megfigyeléséhez azonban az szükséges, hogy vagy jól definiált tömege, vagy impulzusa legyen, ezért a kvarkok „szabadon” nem is lehet megfigyelni, csak kötött állapotban, azaz hadronok alkotóiként. Tulajdonságaikra majd az összetett részecskék tárgyalásánál térek ki.

Összetett részecskék: a hadronok világa

Az összetett „elemi” részecskéknek két alaptípusa van, a két kvarkból (pontosabban kvarkból és antikvarkból) felépülő S = 0, vagy S = 1 spinű mezonok és a három kvarkból, vagy antikvarkból felépülő S = ½ illetve S = 3/2 spinű barionok. Az összetettséget úgy értelmezem, hogy ezekben a részecskékben a fénysebességű forgásoknak két illetve három különböző centrumuk van. Az elektromos töltést tekintve a mezonoknak 0 és ±e, a barionoknak 0, ±e és ±2e lehet a töltésük. Tört töltésű hadront tehát nem lehet megfigyelni, azaz valamennyi hadron összességében tiszta királis állapotnak felel meg, azaz olyan kombinációi lehetnek a belső forgási centrumoknak, hogy a megfigyelhető részecskében legalább az egyik királis forgási forma kompenzálódik, de van úgy, hogy mind a kettő. Az utóbbira példa a neutron. Tehát a kísérletileg megfigyelhető részecskék töltés sajátállapotban vannak és emiatt valódi tömeggel is rendelkeznek.

Miből következik, hogy a hadronok összetett részecskék?

Az egycentrumú fénysebességű forgás modell nem enged meg S = 0 illetve S = 3/2 spínű, illetve ±2e töltésű részecskét, tehát az ilyen tulajdonságú részecskék biztosan összetettek, azaz két vagy három forgási centrummal rendelkeznek, de felvethető a kérdés, hogy milyen kísérleti bizonyítékok mutatják, hogy például a proton és a neutron is összetett részecske?

Két ilyen mérés is mutatja az összetett jelleget, az egyik, amikor rugalmas elektronszórási kísérleteket végeztek, ami lehetővé teszi a töltéseloszlás vizsgálatát, a másik a részecskék mágneses nyomatékának mérése. Hasonítsuk össze ezekben a mérésekben az elektron és a proton tulajdonságait. Az elektron-pozitron szóráskísérletekben (Bhabha szórás) azt találták, hogy a mérési pontosság keretein belül a töltés pontszerű. Ez jó összhangban van a kettősforgás modelljével, mert a fénysebességű forgások miatt a Lorentz kontrakció nullára csökkenti a felszínt, miközben a sugár nem változik, hiszen csak a mozgás irányában következik be relativisztikus kontrakció. Ez azt jelenti, hogy van az elektronnak mágneses nyomatéka (a nyomaték megköveteli a véges sugarat), annak ellenére, hogy a szórás kísérletek szerint nulla a felszín. Hasonló kísérleteket végezve a protonnal, amikor elektronokkal bombázzák véges sugarat kaptak a töltéseloszlásra: R_p = 0,87x10^-15 m. Hasonlítsuk össze ezt a sugarat a proton m_p tömegéből számolható sugárral fénysebességű forgást feltételezve: R_Compton = ℏ/m_p.c = 0,21x10^-15 m. Tehát a proton felülete nem nulla, sőt a számolható sugár négyszer nagyobb, mint amekkora sugara lenne a protonnak, ha a részecskét fénysebességű forgás hozná létre. Ebből már következik, hogy a proton összetett részecske. További bizonyítékot ad a mágneses momentum mérése. Kettős forgások miatt elektron esetében a mágneses momentum μ_el = -μ_B = -e.ℏ/2m_el.c. A kísérletek ennél egy ezreddel nagyobb értéket adnak, amit jól magyaráz a kvantumelektrodinamika által bevezetett vákuumpolarizáció. (Lásd: Az elektron anomális mágneses momentuma”. Ha a proton mágneses nyomatékát is a fénysebességű forgásmodell alapján számolnánk, akkor μ_p = μ_N = e.ℏ/2m_p.c lenne az eredmény. A kísérleti érték ettől jelentősen eltér, ugyanis μ_p = 2,793 μ_N. A jóval nagyobb nyomaték azt mutatja, hogy a tényleges sugár nagyobb a proton Compton sugaránál, ha nincs is négyszer akkora, mint amit a szórás kísérletben láttunk. Ez avval függ össze, hogy az „e” töltés a pozitív 4/3e (két „up” kvark) és a negatív -1/3e („down” kvark) töltéséből adódik ki. A töltés semleges neutronnak is van mágneses nyomatéka: μ_n = -1,931 μ_N , ennek oka, hogy a pozitív 2/3e és a negatív -2/3e töltések térbeli eloszlása nem azonos.

A kvarkok szín kvantumszáma

A fermionok alaptulajdonsága, hogy nem lehet két fermion azonos kvantummechanikai állapotban (Fermi féle kizárási elv). Ha a kvarkokat csak a spinjük, töltésük és generációs számuk különböztetné meg, akkor nem lehetne bizonyos barionokat a kvark modellel értelmezni. Erre példa a  Δ++ részecske, aminek spinje S = 3/2 és töltése 2e. Ilyen részecske három „up” kvarkból épülhet fel. Ez azt jelenti, hogy van egy új kvantumszám, amelyik három különböző értéket vehet fel. Ezt a kvantumszámot nevezték el „szín”-nek a látható fény három alapszínének analógiájára. Mivel a barionok egyike sem mutat ilyen tulajdonságot (például az atommagokban nem fordul elő olyan eset, amikor három azonos proton, vagy neutron lenne), a képződő hadronok nem rendelkeznek szín kvantumszámmal, azaz „fehérek”.

Kvarkok zéruspont oszcillációja hadronokban

Elképzelésem szerint minden fizikai jelenséghez valamilyen mozgás és minden fizikai erőhöz valamilyen tehetetlenségi erő tartozik. Kiindulópontom a zérusponti rezgés koncepciója, amelynek értelmében minden kötött rendszerben fellép valamilyen mozgás, például a molekulában az egyes kötések még a zérusponton is rezegnek. Ez alól a kvarkokból felépülő hadronok sem kivételek, ezért a mezonokban a két kvark egymáshoz képest rezeg, míg a barionokban a három kvark egyfajta „körtáncot lejt”. Ezt a körtáncot a tér három irányában történő rezgésekkel, oszcillációkkal lehet leírni. Így a tér három dimenziója már magyarázza, hogy miért éppen három „szín” létezik. A mozgások a hadronokon kívül nem okozzák a részecske gömbszimmetriájának sérülését, ami megköveteli, hogy mezonokban a két kvark ellenütemben rezegjen, ezt írja le a kvantumkromodinamika a „szín” és „komplementer szín” kombinációjaként, míg a barionokban a három térirányú rezgés eredője biztosítja a gömbszimmetriát.

Gluonok az erős kölcsönhatás közvetítői

A kvantumkromodinamika gluonokkal írja le a különböző színű kvarkok kölcsönhatását, amelyek S = 1 spinnel rendelkeznek és tenzoriális tulajdonságúak, mert mindig két „színt” kapcsolnak össze. Ennek felel meg a fénysebességű forgási képben, hogy van egy egytengelyű forgás az egyik irány körül, amelyik átmegy a másik irányba. Ezek a gluonok csoportokba rendezhetők a két index segítségével, amelyből kizárják a totálszimmetrikus kombinációt és így a 3x3 tenzor elemből összesen nyolc különbözőről beszélnek. Természetesen minden nem egyenletes mozgáshoz tartozik tehetetlenségi erő, így a rezgéshez is, ennek ekvivalenciája az erős kölcsönhatással tekinthető az erős kölcsönhatás forrásának.

Kiegészítő írások

A mezonok és barionok különböző típusait írja le a „Barangolás a kvarkok és elemi részecskék világában”, ahol valamennyi összetett részecske tömegét értelmezem a kvarkok renormálási tömegei révén. A „Paradigmaváltás a fizikában: téridő kontra kvantumelv” című írás foglalja össze a blog többi írását linkek megadásával.

Tévedések és tudományos előrehaladás

Tudományos előrehaladás nem lehet meg tévedések nélkül. Amíg eljutunk az igazsághoz gyakran kell végigjárnunk sok tévesnek bizonyuló mellékutat. Minden kutató, amikor valamilyen eredményre jut, állandóan felteszi magának a kérdést: vajon nem tévedek? Nincs olyan elmélet, nincs olyan állítás, amelynek igazsága ne lenne megkérdőjelezhető. Ezért minden kutató újra és újra végigszalad a bizonyítékok rendszerén vajon nem csúszott be valamilyen hiba az eljárásba, nem hagyott-e figyelmen kívül valamit, ami cáfolhatja elgondolásait? Ez az alkotó bizonytalanság, ami túllendítheti a kutatást a holtpontokon, ami elvezethet új eredményekhez, nagy felfedezésekhez is. Bátorság kell az új eredmények kimondásához, bátorság kell a tévedések beismeréséhez is. Akiből hiányzik ez a kettős bátorság nem érhet el igazán jelentős eredményeket. Minden új eredménynek, forradalmian új gondolatnak meg kell vívnia harcát, hogy befogadja a tudományos közgondolkozás. A közgondolkozás alapvetően konzervatív, emiatt gyakran hosszú időre van szükség, amíg egy-egy új koncepció beépül a tudományba. Ez helyes is, mert egyébként túl nagy teret kapnának a „meg nem gondolt gondolatok”, a tetszetősnek tűnő, de hibás, leegyszerűsítő elképzelések, a sajtó által gyakran felkapott áltudományos nézetek.

Mihez kell bátorság a kutatásban?

Nagy bátorságra van ahhoz is szükség, hogy valaki beismerje tévedését, ha kiderül egy hosszan dédelgetett elképzelésről, hogy téves, szemben áll újabb megfigyelésekkel, vagy elméletekkel. Ha valaki erre nem képes nem léphet tovább, akkor elveszíti képességét, hogy új eredményekhez jusson. Nem könnyű megmondani, hogy hol van a határ, hiszen a cáfolat sem abszolút, a cáfolat is cáfolható. Lehet, hogy az először elvetett gondolat végül mégis igaznak bizonyul. Nehéz megvonni a biztos határt. Minden kutatónak önmagával szemben kell kritikusnak lenni. Ennek igazi jutalma, ha hosszas küszködések és tévedések sorozata után valami hirtelen megvilágosodik, ekkor mintha kinyílna előttünk egy új és szebb világ és ebben a megszentelt pillanatban szárnyalni kezdenek az új gondolatok. Ez az a pillanat, amikor a kutató boldognak érezheti megát.

A speciális relativitáselmélethez vezető út

Einstein esetében két példában fogom illusztrálni a bevezetőben megfogalmazott gondolatokat. Az első példa a gravitációs hullámok lehetőségének felvetése volt. A kérdés előzményéhez tartozik a speciális relativitáselmélet megalkotása. Ez csírájában az elektrodinamika Maxwell egyenleteiben már megjelent, mert az elektromos és mágneses mezők differenciálegyenletei úgy kapcsolják össze az teret és az időt, ahogy azt a relativisztikus mechanika is megteszi a kovariancia elvén keresztül. Ezt ismerte fel Lorentz a maga transzformációs törvényével, ami alapján Minkowski bevezette a téridő fogalmát, Poincaré a matematikai formalizmus újította meg és Planck eljutott a tömeg és az energia ekvivalenciájának felismeréséhez az E = m.c² összefüggés által. Einstein volt, aki a különböző elképzelések egységét teremtette meg és kimondta az alapvető elvet, ami a relativitáshoz vezet, nevezetesen a fénysebesség állandóságának törvényét. Kimutatta, hogy valamennyi relativisztikus jelenség mögött, ez az elv fedezhető fel.

A relativitáselmélet speciális változata csak részben „relativisztikus”. Ez alatt azt értem, hogy a törvény független attól, hogy a földi körülmények között, vagy az univerzum bármely pontján alkalmazzuk, csak az a fontos, hogy legyen a vonatkoztatási rendszer sebessége állandó, másképpen szólva alkosson inercia rendszert. Ekkor megadhatjuk a tér és idő koordináták sebességtől függő összefonódását, amikor is a tér koordináták részben átmennek az idő koordinátába és fordítva az idő is részben tér jellegűvé válik. Ennek következtében a megfigyelőhöz képest valamilyen sebességgel mozgó test mérete a megfigyelő mérései szerint lecsökken és tömege megnövekszik.

Miért volt szükség a speciális relativitáselmélet általánosítására?

Einstein tisztában volt a speciális relativitáselmélet korlátaival is, mert a feltételezett inercia rendszer valójában nem is létezik. A Földhöz nem köthetjük, mert a Föld forog saját tengelye és kering a Nap körül, a Nap sem jó választás, mert keringő mozgást végez a Tejút rendszerben, a Tejút középpontja sem jó, mert a különböző galaktikák egymáshoz képest is végeznek különböző nem egyenletes sebességű mozgásokat. Ezért szükségét látta, hogy olyan elméletet dolgozzon ki, amely a gyorsuló vonatkoztatási rendszerben is alkalmazható. Ezt kapcsolta össze a gravitáció eredetének magyarázatával. Kimondott egy általános elvet, ami megalapozta az általános relativitáselméletet: a gravitáció ekvivalens a gyorsuló rendszer tehetetlenségi erejével. Ezt úgy szemléltethetjük, ha valaki egy űrhajóban utazik távol minden gravitációs mezőtől és az űrhajó pont a földi nehézségi gyorsulással halad, akkor ugyanakkora erő hat rá, mintha a Földön lenne. Az ekvivalencia elv azonban magával hozta a tér és idő összekapcsolásának új formáját, ezek a koordináták másképpen csatolódnak össze, amikor a szóban forgó rendszerben fellép a gravitáció, illetve a gyorsulás. Ez a másféle kapcsolódás a téridő koordináták lokális görbületével írható le. Az ekvivalencia elv szerint nem számít az anyag minősége, csupán a tömege. A tér nem jellemezhető az euklideszi egyenes koordinátákkal a téridőt torzító tömeg jelenléte miatt. A tömeg eloszlása határozza meg a görbült teret, de ez a görbület visszahat a tömegek mozgására is. Ez az oda-vissza való hatás jelenik meg az Einstein féle gravitációs egyenletben, ami rendkívül megnehezíti a probléma matematikai kezelését és különböző elvi problémák kiinduló pontja is.

Az általános relativitáselmélet következményei

Egyszerűbb esetben, amikor a nagytömegű Nap körül vizsgáljuk a viszonylag kis tömegű bolygómozgást a megoldás jó közelítésben megadható. Einstein megvizsgálta a Merkúr pálya perihéliumának (az ellipszis pálya napközeli pontja) vándorlását, amelyet pontosabban tudott megadni, mint ami a Newton egyenletből számolható. A másik kísérleti bizonyítéknak tekintették, hogy Einstein elmélete magyarázni képes a gravitációs fényelhajlást. Ez napfogyatkozás esetén vizsgálható, amikor a Nap által eltakart csillag fénye megfigyelhető, mert az onnan érkező fotonok pályája a gravitációs térben elhajlik és így megkerüli a Napot. Ennek konkrét megfigyelése után vált Einstein elmélete általánosan elfogadottá, ami azért érdekes fordulata a fizika történetének, mert kiderült, hogy a Newton egyenlet alapján is lehet értelmezni a fényelhajlást, amelynek mértéke fele az Einstein elméletéből következő értéknek, viszont a mérési pontosság korlátai sokáig nem tették lehetővé, hogy ez alapján különbséget lehessen tenni a két elmélet között. Csak 1960-ban igazolták Pound és Rebka mérései [1], hogy tényleg az általános relativitáselmélet előrejelzése a helyes.

Einstein gravitációs egyenletének sajátságai

Kövessük Einstein egyenletének további alakulását és vizsgáljuk meg, hogy milyen elvi problémák keletkeznek ebből! A tömegek pozíciója és sebessége adja az egyenlet forrásoldalát, amit matematikailag az energia-impulzus tenzor T_ab ír le, ahol az alsó index a görbült téridő koordinátáit jelöli. Ez alapján kell meghatározni a g_ab metrikus tenzort, ami a koordináta szorzatok együtthatója. A speciális relativitáselméletben (Minkowski téridő) g_ab egy négydimenziós diagonális mátrix: (1, -1,-1,-1) sajátértékekkel, ahol az első index az idődimenziónak felel meg. Ha ismerjük a görbült tér  g_ab metrikus tenzorát, akkor ebből parciális deriválások segítségével képezhetjük az R_ab görbületi tenzort, amit Ricci tenzornak nevez az irodalom. Az eredeti Einstein egyenlet:

 Az egyenletben G az általános gravitációs állandó és R a Ricci tenzor diagonális elemeinek összege.

A gravitációs egyenlet elvi problémái

Az elvi és a számítási nehézségek abból fakadnak, hogy a T_ab tenzort az ismeretlen térgeometria koordinátáival kell kifejezni! Mintha a fizikusnak egy ismeretlen szerkezetű ingoványon kellene átkelni, ahol nem tudja, hol talál szilárd talajt. Ha egy vigyázatlan lépéskor süllyedni kezd, mozgásával megváltoztatja a szilárd és a képlékeny részek eloszlását (tehát átrendezi a tér geometriáját) és ha ráadásul ijedtében kapálózni kezd, csak meggyorsítja a süllyedést. Matematikailag ez a „rossz lépés” a kezdő feltételek rossz megválasztásának felel meg. Kijöhetnek olyan matematikai megoldások is, amelyek visszavezetnek a múltba, ami az ismert paradoxonhoz vezet: a múltban tehetnék valami olyat, ami megakadályozná saját megszületésemet, de akkor hogy mehetnék vissza a múltba, ha meg sem születtem? A nehézség valójában a g_ab tenzor nagy szabadsági fokából származik, mert a szimmetrikus mátrixnak 10 független eleme van, viszont a fizikai tér – az elektrodinamikához hasonlóan – csak két szabadsági fokkal rendelkezik [2].

A kozmikus állandó

Einstein megkísérelte az univerzum egészére alkalmazni egyenletét, de azt kapta, hogy az univerzum összezuhan, vagy szétszalad, ami ellenkezett koncepciójával, mert az univerzumot sztatikusnak képzelte. Emiatt kiegészítette az eredeti egyenlet bal odalát egy új taggal:λ g_ab, amelyben λ a kozmikus állandó. Néhány évvel később Hubble a távoli galaxisok vörös eltolódása alapján kimutatta, hogy az univerzum tágul és nincs szükség a kozmikus állandó fogalmára. Einstein azonnal elismerte tévedését és a kozmikus állandó bevezetését élete legnagyobb tévedésének nevezte. Az utókor mégis igazat adott Einsteinnek a kozmológiai állandó létezését illetően, mert a távoli szupernóva robbanások vörös eltolódása arra mutat, hogy az univerzum gyorsulva tágul, ami csak úgy értelmezhető, ha mégis szerepet játszik a kozmikus állandó.

Gravitációs lencse és az Einstein gyűrűk

Einstein kereste az analógiát az elektromágnesesség és a gravitáció között és kimutatta, hogy az optikának megfelelő effektusokat a gravitáció is okozhat extrém anyagsűrűség esetén. Szintén a gravitációs egyenletből következik, hogy nagy tömegsűrűség akkora gravitációs mezőt hozhat létre, amely már a fényt is foglyul ejtheti, ezek a fekete lyukak. Az a fény, amely elhalad a fekete lyuk mellett, erősen elhajlik és fókuszálódik, és így gravitációs lencsehatás jön létre. A lencsehatás megnyilvánulása, hogy a fekete lyuk mögötti galaxisról gyűrű alakú formációk képződnek. Ilyen gyűrűket valóban sikerült is megfigyelni igazolva Einstein hipotézisét.

A gravitációs hullám

Talán a legtöbbet vitatott és keresett jelenség, amit szintén Einstein mutatott ki a gravitációs hullám. Ez a téridő görbületének hullámszerű terjedése. A gravitációs állandó gyengesége miatt ez rendkívül gyenge hatás, maga Einstein is szkeptikus volt, hogy egyáltalán megfigyelhető-e a jelenség, de fontosnak tartotta, mert a görbült téridő létezésének egyik bizonyítékát látta benne. Két alkalommal is publikálta felvetését, mert először matematikai hibát vétett a számításban. Tévedését két évvel később aztán korrigálta. Ez is jellemzi Einstein viszonyát eredményeihez: ha valamiben tévedett azt hajlandó volt elismerni és továbblépni!

Sokan, sokféleképp akarták kimutatni a gravitációs hullámokat, mások kételkedtek benne, hogy egyáltalán létezik. Ennek oka, hogy az elektromágneses hullámokkal való analógia nem teljes. Amint arra Mayer István felhívta figyelmemet, a gravitációs mező sajátenergiája – szemben az elektromágneses mezővel [3,4] – negatív és ez lehetetlenné teszi, hogy a Minkowski féle téridőben kialakuljanak gravitációs hullámok, más szóval a gravitációs hullámok a klasszikus fizika vagy a speciális relativitáselmélet keretében nem értelmezhetők, csakis az általános relativitáselmélet ad rájuk magyarázatot. Mégis többször vélték úgy, hogy sikerült a jelenséget kimutatni, de rendre kiderült, hogy téves volt az értelmezés. Az első meggyőző bizonyítékot a LIGO kísérlet adta meg [5]. Ez azért különösen jelentős, mert ezek a hullámok a téridő görbültségének közvetlen bizonyítékai, hiszen a Minkowski téridőben nem jöhetnek létre.

A LIGO kísérlet nehézségei

A LIGO kísérlet értelmezéséhez induljunk ki a rövidítést takaró egyes szavakból: Laser Interferometer Gravitational wave Observatory. A mérés rendkívüli pontosságot igényel, mert az atommag méretével egybevethető pontosságú távolságmérésre van szükség. A másik nehézség elvi jellegű: ha maga a tér nyúlik meg, vagy rövidül, akkor ez mérési eszközünket is megváltoztatja, így a hullámokat egyetlen „mérőrúddal” nem is észlelhetjük. Viszont a tér görbül, ami avval jár együtt, hogy különböző irányokban eltérő lesz a hatása. Emiatt egy „L” alakú elrendezést kell használni és összehasonlítani a két „rúd” hosszának változását. A rudakat jó hosszúra kell választani (a LIGO-ban ez 4-4 km), mert az effektus a rúd teljes hosszával arányos. A rúd teljes hosszának változását elvileg sem láthatjuk, de mód van a két rúd hosszának különbségét követni. Ehhez kell a laser forrás és az interferométer. Az „L” alakzat közepéről sugarat kell kibocsátani mindkét irányban, majd a rúd végeken lévő tükrökkel visszavetíteni a sugarakat a találkozási pontig és ott interferenciát létrehozni. Ehhez monokromatikus és koherens sugarakra van szükség, amit a laser sugárzás biztosít. Pontos hangolással el lehet érni, hogy a két sugár épp kioltsa egymást, ezt oldja meg az interferométer. Ez a hídelv rendkívül nagy pontossággal észleli, ha a két rúd hossza eltérő mértékben változik. A mérés nagy pontossága persze veszélyforrás, mert a legkisebb külső rezgés, vagy a 4 km hosszú rúdon egy kis hőmérsékletkülönbség is hamis jeleket fog létrehozni. Emiatt szükséges, hogy legalább két távoli helyen (ez 3000 km volt) működjön két ilyen berendezés, aminek jele egyidejűleg jelentkezik, ha a változást tényleg a gravitációs hullámok okozzák. Emiatt ezer kutató munkájára és különleges elővigyázatosságra volt szükség, hogy a hamis jelek garmadájából kiválasszák a valódi effektust.

Részecskék mint a téridő fénysebességű forgásai

A sikeres mérés ismét Einsteint igazolta, de ennél fontosabb, hogy a fizika biztosan támaszkodhat a téridő görbületének elvére. Magam is ebből indultam ki, amikor a részecskéket úgy értelmeztem, mint a tér fénysebességű forgásait, ami extrém mértékű térgörbületet hoz létre [6]. A koncepció kiinduló pontja a Minkowski téridő, ezért ment azoktól a problémáktól, amelyek a makroszkopikus Einstein egyenletből származnak, ahol a görbület forrását adó energia-impulzus tenzor az ismeretlen és változó görbületű téridőben van definiálva. Mivel a részecskéket létrehozó forgások az identikus geometriára támaszkodnak így biztosítva van, hogy bárhol képződik a részecske a tulajdonságok azonosak lesznek. Az Einstein féle gravitáció másodlagos hatás, ahol a lankás görbületek rárakódnak a részecskéket alkotó éles görbületekre. Ez a koncepció elkerüli az Einstein egyenlet által megengedett szingularitást is, mert a másodlagos (gravitációs) forgás hatása nem haladhatja meg az elsődleges, fénysebességű forgásét, hiszen az annál is nagyobb centrifugális erőt már a görbült téridő nem tudná kiegyenlíteni. Ez összhangban van a Planck hossz definíciójával, ami behatárolja a fekete lyuk modellben a maximális gravitációs erőt és tömegsűrűséget [7].

 A következő bejegyzésben lesz szó az EPR paradoxonról.  

Ajánlott irodalom

1. R. V. Pound, G. A. Rebka: „Apparent weight of photons”, Phys. Rev. Lett., 4, 337-341 (1960).
2. A téma iránt érdeklődőknek ajánlom Szabados B. László kitűnő összefoglalóját (Magyar Tudomány: „Száz éves az általános relativitáselmélet). Az írás néhány gondolatát a bejegyzésben felhasználtam.
3. I. Mayer: A Connection between Special Theory of Relativity and Quantum Theory”, arXiv-1207.3180v2.pdf
4. P. G. Peters: „Where is the energy stored in a gravitational field”, Am. J. Phys. 49, 564 (1981).
5. „Gravitational waves detected 100 years after Einstein’s prediction”, LIGO 11 February 2016.
6. A. Rockenbauer: „A screw model for quantum electrodynamics: From gravitation to quanta”, INDIAN JOURNAL OF PHYSICS, 89, 389-396 (2015)
7. A "Paradigmaváltás a fizikában: téridő kontra kvantumelv” című bejegyzés foglalja össze azokat az írásokat, ahol további információ található a témában.

A görbült tér víziója

A LIGO kísérlet margójára

Most, hogy a LIGO kísérletben sikerült kimutatni a gravitációs hullámok létezését újra ráirányult a figyelem Einstein koncepciójára, aki a gravitációt a tér torzulásával magyarázta. Einstein ezt az elvet nagyjából egy időben dolgozta ki a kvantummechanika megszületésével, amelyik elmélet sikeresen magyarázta a mikrovilág szokatlan jelenségeit. Mivel a görbült tér koncepciója a klasszikus fizika fogalmain alapult, ezért a fizikusok többsége úgy gondolta, hogy a gravitációt is ilyen keretek között kellene értelmezni, hasonlóan a további három kölcsönhatáshoz: ugyanis az elektromágneses, a gyenge- és erős kölcsönhatás egyaránt leírhatónak bizonyult a kvantumelv alapján. Az erőfeszítések azonban sikertelenek maradtak, aminek elvi okát abban látom, hogy a tér torzulása az elsődleges fizikai elv minden kölcsönhatás magyarázatára, míg a kvantumosság csak ennek speciális megnyilvánulása. Más szóval nem a gravitációt kell visszavezetni a kvantumelvre, hanem fordítva a kvantumot kell úgy tekinteni mint a tér extrém torzulásának következményét. Erről írtam már korábbi bejegyzésekben.

A LIGO kísérlet jelentősége

A LIGO kísérlet sikere nyomán azt szokták hangsúlyozni, hogy ez új utat nyit a fizika számára, mert ezáltal nem csak az elektromágneses hullámok fogják szolgáltatni ismereteinket az univerzum titkairól, hanem a gravitációs hullámok is. Magam nem ebben látom a gravitációs hullámok jelentőségét, már csak azért sem mert rendkívül speciális követelményeknek kell eleget tenni, hogy bizonyossággal mondhassuk, valóban gravitációs hullámokat figyeltünk meg, hiszen rengeteg zavaró körülményt kell kiküszöbölni, hanem abban látom, hogy ezáltal fizikai törvényeink univerzális érvényét sikerült alátámasztani, ami reményem szerint elvezet oda, hogy a fizika felismerje a görbült tér koncepciójának elsőbbségét a kvantumelv felett.

A gravitációs hullámok észlelése

A rendkívül nagy műgonddal elvégzett és igencsak költséges kísérlet ( 1 milliárd dollárt és ezer kutató munkáját igényelte) tehát eredményes volt. Talán csak azt lehet kifogásolni, hogy miért csak két pontján a Földnek állították fel a berendezést és nem például három, vagy négy helyen. Ugyanis a tér hullámzása által előidézett rendkívül kis effektust kellett kiszűrni sokkal nagyobb zavaró hatások közül, ahol a szűrésben döntő szerepe volt a jelenség egyidejű jelentkezésének, amit nagyobb biztonsággal lehetett volna elérni több megfigyelő állomás segítségével. Nyilván a költségek nagysága volt ennek akadálya.

Az einsteini idea és kapcsolata az elektromágneses hullámokkal

A gravitációs hullámok létezésének esélyét Einstein vetette fel mint gravitációelméletének egyik következményét. A gravitációs hullámok létezésének gondolatához azonban egyszerűbben is eljuthatunk. Itt az elektromágneses kölcsönhatás és a gravitáció törvényének hasonlóságára utalok. Két töltés között létrejövő erőhatás a töltések szorzatával arányos és csökken a töltések távolságának négyzetével:

F_Coulomb= q.Q/R²

 Hasonlítsuk ehhez Newton gravitációs törvényét: eszerint két tömeg között a vonzó erő a két tömeg szorzatával és szintén a távolság négyzetének reciprokával arányos:

F_Newton =γm.M/R²

 Tehát ha a töltések helyett tömegekre gondolunk, akkor az elektromosság Coulomb törvényéből a tömegvonzás törvényéhez jutunk. A fő különbség természetesen a két kölcsönhatás erősségének eltérése, amiért a mikrovilágban, például az atomok között a gravitáció elhanyagolható mértékű (negyven nagyságrenddel kisebb) hatást idéz elő. A másik eltérés, ami viszont a gravitáció javára szól, hogy mindig vonzást jelent, míg töltések esetén lehet vonzás és taszítás is a töltések előjelétől függően. Mivel univerzumunkban (legalább is földi körülmények között) a pozitív és negatív töltések egyensúlya alakult ki, így makroszkopikus méretekben már kompenzálódik az elektromos töltések hatása, viszont a gravitáció mindig összeadódik, és döntő szerepre tesz szert a csillagok és a bolygók közötti erőhatásokban.

A speciális relativitáselmélet szerepe az erőtörvényekben

A másik törvény, amelyik egyaránt érvényes a két kölcsönhatásra a speciális relativitáselmélet, aminek kiindulópontja, hogy a hatások terjedési sebessége c-vel, azaz a fénysebességgel egyenlő. Ennek alapvető szerepe van az elektromágnesesség törvényeiben és az elektromágneses hullámok kialakulásában. Ha egy töltés mozog a másik töltéshez képest, akkor annak hatása késleltetve jelentkezik. Ha például a töltések távolsága R, akkor a részecske Δt = R/c idővel korábbi pozíciója határozza meg a kölcsönhatás erejét és irányát. Ez a pozíció, ha a sebesség u, a pillanatnyi helyzethez képest a Δs = u. Δt = R.u/c mértékében tér el. Itt is, ahogy a relativisztikus egyenletekben általános az u/c sebességek aránya határozza meg az effektus mértékét. Ez a hatás korrigálja a Coulomb kölcsönhatást, mert a q töltés felé mutató erőhöz – amit az E elektromos mezővel írunk le: F_Coulomb = q.E –  hozzá kell venni egy akkora erőt, ami által a két erő együttese már az említett korábbi pozícióba mutat. Ezt a kiegészítő erőt jellemezzük a B mágneses mezővel, amit a Lorentz erőnek nevezünk: F_Lorentz = q.Bxu/c , ahol az aláhúzás vektorokat, az „x” művelet pedig vektorszorzatot jelöl. Az elektromos és mágneses mezők képződését a töltésekből és áramokból (ez a q töltés és az u sebesség szorzata), valamint a két mező időbeli változásának hatását a négy Maxwell egyenlet adja meg. A Maxwell egyenletek pedig magyarázzák az elektromágneses hullámok keletkezését.

A gravitációs mező szerkezete

A logikai út tehát a Coulomb törvényből, a relativisztikus effektuson át elvezet az elektromágneses mező fogalmához és végük az elektromágneses hullámokhoz is. Elvben hasonló utat bejárhatunk a tömegvonzás Newton törvényéből kiindulva és bevezethetnénk gravitációs és gravi-mágneses mezőket, átírhatnánk a Maxwell egyenleteket és levezethetnénk a gravitációs hullámokat is.

Szemléletes példák a relativisztikus hatásra a gravitációban

Szemléltessük a relativisztikus hatást a Nap és a Föld példájával. A Föld keringési sebessége 30 km/s, azaz 10 000 szer lassabb, mint a fénysebesség. A Nap átlagos távolsága 150 millió km, ezért onnan a fény 500 másodperc alatt ér el a Földre, a Nap tényleges helyzete pedig 15 000 km-rel van arrébb, mint ahol látjuk, ez kis érték a Nap 700 ezer km sugarához képest. A gravitáció és a fény terjedési sebessége megegyezik, ezért a vonzás iránya pontosan megegyezik avval az iránnyal, ahol a Nap centrumát látjuk. A Lorentz kontrakció miatt a Föld egy év alatt megtett pályájának hossza 5 km-rel lesz rövidebb, ha ezt a Naphoz kötött és nem keringő rendszerből nézzük.

Einsteini magyarázat a gravitációra

Einstein nem a Maxwell egyenletek mintájára írta le a gravitációt, mert ő mélyebbre ásott, és a formális átírás helyett a gravitáció forrását kereste, amit megtalált a görbült tér fogalmának segítségével. A tömegeloszlás és a görbült térkoordináták között felírt gravitációs egyenlet pedig elvezetett a gravitációs hullámokhoz, evvel demonstrálva, hogy az elektromágneses és a gravitációs erők fizikai alapja közös. Ettől válik a LIGO kísérlet fontossá, amely megerősíti meggyőződésemet is, hogy a fizikai világ természetének megértéséhez a tér görbületéből kell kiindulni, a görbület pedig csak akkor létezik, ha a tér és az idő folytonos.

A görbült téridő víziója kétdimenziós világban

Képzeljük most magunk elé a görbült téridő világát. A háromdimenziós teret az idő dimenziójával már a speciális relativitáselmélet is összekapcsolja, és ezért használjuk a téridő fogalmát. Az általános relativitáselmélet tovább mélyíti ezt a kapcsolatot, mert függővé teszi a gravitációtól, illetve a gyorsulástól is. (Az általános relativitáselmélet a gravitációt és a gyorsulás által keltett tehetetlenségi erőt ekvivalenciába hozza.) A háromdimenziós tér torzulását nem tudjuk elképzelni, ezért legyen a világ kétdimenziós és a harmadik dimenzió legyen a görbület. Ebben a világban minden részecskét egy-egy kör reprezentál, és minél nagyobb a részecske energiája, azaz tömege, annál kisebb a kör sugara, de nagyobb a bemélyedése.

A kvarkok tánca

Képzeljük el először a kvarkokat. A kvarkok hármas táncát látjuk a protonok és neutronok sokaságában. Három tűszerű hosszú cső körtáncot lejt egymás körül olyan szorosan, hogy a középpontjaik által alkotott kör sugara kisebb, mint a táncban résztvevő egyes köröké. Ez a tánc tartja stabilan együtt a hármast. Ez a kép illusztrálja, hogy a kvarkokhoz rendelt tömegek összege jóval kisebb, mint a belőlük képzett protonoké vagy neutronoké. Elvétve láthatunk kettesben, vagy más hármasban táncoló kvarkokat is, ahol az egyes kvarkok sugara még kisebb és a cső hossza még nagyobb, de ezek gyorsan szétesnek, vagy átalakulnak, miközben az eredeti kör eltűnik. Létrejönnek azonban gyorsan száguldó körök, a gamma sugarak, amelyek aztán bejárják az univerzumot.

Az atommagtól a csillagokig

De szemléljük tovább ezt a görbületi világot! A hármas táncot lejtő együttesek is összekapcsolódnak, lehetnek akár összetapadva kétszázan is. Az egyes kvark-körök átugrálhatnak a hármas csoportok között és ezzel egyben tartják a nagyobb társaságot. Ezek a különböző atommagok. Ezeket a csoportokat nagyobb sugarú, de kevésbé mély csövek veszik körül, az elektronok, megalkotva az atomokat. Ezek a vastagabb és rövidebb csövek olyan mozgékonyak, hogy képesek összekötni az atomokat, létrehozva kisebb, vagy nagyobb molekulákat is. A molekulák nagyobb csoportjai is egymáshoz társulnak, továbbra is mozogva a folyadékokban, vagy szilárdan összetartva a szilárdtestekben. Van ahol olyan heves az atommagok tánca és egymásba alakulása, hogy nem kötődhetnek hozzá az egyes elektronok, ez a plazma állapot, ami alkotója a csillagoknak.

Einstein víziója a gravitációs mezőről

Minden elemi csövet egy lankás görbület vesz körül, de ezek összeadódhatnak megalkotva bolygókat és csillagokat. Ezt a lankás tájat álmodta meg Einstein megmagyarázva a nagyobb csoportokat összetartó gravitációs erőt. De vannak olyan helyek is, ahol annyira sűrű a csoportok összetapadása, hogy mély görbület jön létre, amelyik még a száguldó foton-köröket is féken tudja tartani. Ezek a fekete lyukak, amelyek egymásba kapcsolódása úgy rázkódtatja meg a görbült világot, hogy annak hullámai eljuthatnak hozzánk is a Földre. A lankás táj összessége átfogó görbületet hoz létre, ami összekapcsolja a csillagokat megalkotva a galaktikákat. Ezek is további csoportokat alkotnak a nagy univerzumban, de ezek a csoportok egymástól távolodnak kitágítva evvel az univerzum terét.

A téridő ingadozása

De nézzük meg közelebbről is az atomokat körülvevő tájat. Azt látjuk, hogy a száguldó, képződő és elnyelődő foton görbületek állandó ingadozást hoznak létre a görbületi struktúrában. A görbületi ingadozásokat írják le a kvantumelektrodinamikában mint a vákuum polarizáció jelenségét. A kvarkok kettes és hármas csoportjain belül is átalakulások jönnek létre, miközben rendkívül rövid időre egy nagyon hosszú cső keletkezik, amelyik azonban tágulni kezd, miközben hosszúsága csökken, majd végül eltűnik létrehozva új kör alakú csöveket. Ez a gyenge kölcsönhatás világa.

Megjegyzés: A korábbi bejegyzések összefoglalását lásd: „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”

A Dirac egyenletről már szó volt a korábbi bejegyzésben: „A Dirac egyenlettől az általános fermion egyenletig”, de most visszatérek erre a témára, mert a mikrovilág fogalmi rendszere szempontjából alapvető, hogy jól értsük, ez az egyenlet valójában miről is „szól”.

Az energia két alapformája

Az energiát két tag összegeként értelmezzük, az egyik, amelyik a mozgások következménye, ez a kinetikus energia, a másik valamilyen erőmezőben való pozíciótól függ, ezt nevezzük potenciális energiának:

E = E_kin + E _pot

Az általam javasolt fénysebességű forgásokból felépülő részecskekoncepció szerint a fizikai objektum elemi összetevői maguk is végeznek valamilyen belső – fénysebességű – mozgást. Ez a belső mozgás azonban nem szerepel a hagyományos fizikai képben, ezért pontosítani kell az előző megfogalmazást: egyfelől a kinetikus energia a külső (tehát szokásos) és belső (vagy saját) mozgások együttesét tartalmazza, másfelől a potenciális energiában a pozíciófüggésen kívül burkoltan megjelenik a belső mozgások hatása is.

Az energia relativisztikus törvénye

A relativisztikus mechanika alaptörvénye az energia kovariáns alakjára épül:

E² = c².p² + m²₀.c⁴

ahol az első tagot tekintik a relativisztikus kinetikus energiának, a másodikat a részecske nyugalmi energiájának. A fénysebességű forgásmodellben ez új értelmet nyer, mert nyugalmi energia helyett a belső mozgástól származó kinetikus energiáról kell beszélni, azaz a kinetikus energia két tagból tevődik össze:

E²_kin = E²_külső + E²_belső

A két tag négyzetes összeadási szabálya azt fogalmazza meg, hogy a teljes impulzus két tagja p = p_külső + p_belső úgy összegződik négyzetre emeléskor, hogy a kereszt tag eltűnik. Ennek azaz oka, hogy a belső mozgás gömbszimmetrikus pályán történik, aminek átlagértéke nulla és csak a belső mozgás impulzusának négyzete rendelkezik nullától különböző értékkel.

Az elektromágneses mező energiája

A Dirac egyenlet az elektron elektromágneses mezőben való mozgását írja le, ami szükségessé teszi a klasszikus elektrodinamika Maxwell egyenleteinek alkalmazását. Ezek az egyenletek eleget tesznek a relativisztikus kovariancia elvnek, amiért az elektromos és mágneses mező által keltett energiát hozzávehetjük a mechanikai energiához. A mozgásból származó tagot, ami a kinetikus energiához ad járulékot az áramok (töltésmozgás) képviselik és ezt az A(r) vektorpotenciál képviseli, aminek a töltéssel való szorzata adja meg az energiát. Lényeges, hogy bár vektorpotenciálról beszélünk, ez a tag nem potenciális energia, mert a mágneses mező a mozgó töltésekre hat és a töltés mozgása által jön létre, így a kinetikus energiához ad járulékot. Az energia kifejezésben a vektorpotenciált a töltéssel szorozzuk, amelyet viszont a részecske sajátmozgásának tulajdonítunk a fénysebességű forgásmodellben. Emiatt az e. A(r) tag voltaképp a külső és belső mozgások csatolódása. Az elektromos mezőben való energiát a Φ(r) skaláris potenciál és a töltés szorzata adja meg, és ez a töltésen keresztül szintén függ a belső mozgástól, de nem függ a külsőtől, emiatt az e.Φ(r) tag a potenciális energiát határozza meg. Így kapjuk meg a klasszikus elektron kovariáns energiaformuláját:

(E – e.Φ(r))² = (c.p – e.A(r))² + m²₀.c⁴

A kovariáns egyenletben tehát azt kell látni, hogy a Φ(r) potenciál a vizsgált rendszerben lévő töltések, az A(r) vektorpotenciál pedig az áramok eloszlását írja le, a p impulzus a vizsgált részecske külső térbeli mozgásmennyisége, az e töltés és az m₀ nyugalmi tömeg a részecske sajátmozgását fejezi ki.

A relativisztikus energia kvantummechanikája

A fenti egyenlet kvantummechanika átírását Klein és Gordon adták meg, de egyenletük nem volt kezelhető a szokásos sajátérték módszerrel az energia négyzetes alakja miatt. Ezt oldotta meg Dirac, amikor a négyzetgyökvonást 4x4 dimenziós spinorokkal hajtotta végre. Szemléletesebb képet kapunk, ha a spinorokat felbontjuk Pauli mátrixokra a mátrixok direktszorzat művelete alapján. Ekkor a Dirac egyenlet:

H_D = c.σ_x*σ(p – e.A(r)) + σ_z*I.m₀.c² + I*I.e.Φ(r)

Itt * a direktszorzást, a vastag betű a vektorokat, az aláhúzás mátrixokat jelöl, külön feltüntettem az I kétdimenziós egységmátrixot is. A direktszorzatban lényeges a tényezők sorrendje is. A Pauli mátrixok alakja:

Alapvető jelentősége van a Dirac egyenletben, hogy az impulzus tagban σ_x, míg a nyugalmi energiában σ_z szerepel, ugyanis a két mátrix szorzatában a tényezők sorrendje nem cserélhető fel. Ebből származik a mozgási tömeg sebességfüggése ( lásd „A Dirac egyenlettől az általános fermion egyenletig” című bejegyzést.)

Kétértékűségek megjelenése az energiában és a lyukelmélet

 A négyzetgyökvonás sajátsága a kétértékűség, mert a negatív és pozitív számok négyzete azonos. A négyzetgyökvonás kétértékűségét azáltal őrzi meg a formalizmus, hogy a diagonális σ_z mátrixban a két elem előjele fordított, és így szükségképpen lesz pozitív és negatív energia. Abból az elvből kiindulva, hogy a nagyobb energiájú állapotból a rendszer spontán módon átmegy az alacsonyabb energiájú állapotba az következik, hogy az elektron előbb utóbb végtelenül nagy negatív energiájú állapotba ugrik, azaz megsemmisül. Ez viszont ellentétes a tapasztalattal, amely szerint az elektron stabilis részecske. Emiatt állt elő Dirac avval a hipotézissel, hogy a végtelen számú negatív energia állapot már eleve be van töltve a vákuumban és a Pauli elv kizárja, hogy az elektron a negatív energiájú pályára ugorjon. Ez persze azt jelenti, hogy a vákuum végtelenül nagy negatív tömeggel rendelkezik, ami mutatja a hipotézis abszurditását. A meghökkentő hipotézis mégis igaznak látszott, mert mintegy „megjósolta” egy új részecske létezését, amit nem sokkal később felfedeztek, nevezetesen a pozitront. Itt a lyukelméletről van szó, hiszen ha a negatív energiájú elektrontengerből hiányzik egy részecske, akkor az pontosan a pozitronnak felel meg (azonos a tömege, de ellentétes az előjele az elektronhoz képest) és még az is érthetővé válik, hogy az elektron és pozitron ütközése miért vezet a két részecske megsemmisüléséhez.  

A lyukelmélet látszólagos igazolása két fontos tanulsággal is jár. Egyfelől nagyon óvatosnak kell lenni, hogy mikor tekintünk egy elméletet bizonyítottnak, másfelől nem árt, ha a fizikusok is hallgatnak időnként a józanész szavára.

Negatív energia és az időtükrözés

Először is nézzük meg, hogyan lehet a negatív energia megjelenését magyarázni a formalizmusban? Az energia kovariáns egyenlete négyzetes tagokat tartalmaz, ezért van negatív energiájú megoldás a négyzetgyökvonás kétértékűsége miatt. A kvantummechanika mint hatást definiálja az energiát, amely arányos az idő szerint differenciálhányadossal: ℏid/dt. Ez azt jelenti, hogy a negatív energia az idő irányának megfordításának felel meg, más szóval a kovariáns reláció nem tudja megkülönböztetni, hogy a jelenből a jövő felé, vagy fordítva a múlt felé vesszük az irányt. Az már a legősibb tapasztalatok közé tartozik, hogy nem lehet visszatérni a múltba. Emiatt az alkalmazott matematikai formalizmust kell kiegészíteni egy kiválasztási szabállyal, ami megtiltja a negatív energiájú állapotba való átmenetet, és nem fordítva a természettől kell elvárni, hogy engedelmeskedjen egy matematikai egyenlet követelményeinek. Ennyit a józanészről. A másik kérdés hogyan magyarázzuk az elektron-pozitron annihilációt. Ez már a kettősforgás teóriájából következik. Minden kettősforgás két alapszimmetriával rendelkezik a két forgás egymáshoz képesti viszonya miatt, amit jobb és balkéz kiralitásnak nevezhetünk. A két részecske ütközésekor az ellentett forgások megsemmisítik egymást és így csak egyetlen forgás marad fent, amit a fénysebességű forgásmodellben mint fotont értelmezünk.

A spin és az időtükrözés

Elemezzük tovább a Dirac egyenletet! Az impulzus is négyzeten szerepel, ezért az impulzusnak is kétféle előjele lehet. Ezt fejezi két a második tényező σ, ami az elektron spin definíciójához vezet. A spin két forgásirányának tükrözését tekinti a kvantummechanika az időtükrözés műveletének. Ezt az időtükrözést meg kell különböztetni az energiára vonatkozó megállapítástól, mert az energia esetén a külső és belső mozgás együttes megfordításáról van szó, míg a spin esetében csak a külső mozgás ideje fordul meg.

Kettősforgások a királis térben: az általános fermion egyenlet

Az általános fermion egyenlet felírásánál 8x8-as spinorokat használtam, amelyben még fellép egy a Pauli mátrixokból felépített unitér mátrix is, amely definiálja a töltés és a tömeg operátorát. Ennek eredete a kovariáns egyenletben, hogy a nyugalmi tömegre vonatkozó tag is négyzetes, azaz itt is fent áll a kétértékűség, amiért egy harmadik kétdimenziós mátrix bevezetése is szükséges a teljes leíráshoz.  Ez az új mátrix nem az időhöz, hanem a térhez kapcsolódik és annak kétféle királis szimmetriája (jobb és balkezű) határozza meg a részecskék szerkezetét, azáltal hogy megmondja, milyen arányban részesül a két alapszimmetria a részecskét meghatározó kettősforgásban. Az elektron és pozitron tiszta királis állapot (jobb vagy balsodrású), a neutrínóban a két kiralitás kioltja egymást, míg a kvarkok képviselik a két kiralitást aszimmetrikusan tartalmazó forgásállapotot. Ennek megfelelően beszélünk tömeg, illetve impulzus sajátállapotú részecskékről. A tömeg sajátállapot egyúttal a töltés sajátállapotot is jelenti. A neutrínó nincs sem töltés, sem tömeg sajátállapotban, de jól definiált impulzussal rendelkezik, ez magyarázza, hogy létezhet három különböző neutrínó bár tömegük várható értéke nulla. Megfigyelhető részecskéknek vagy tömeg, vagy impulzus állapotban kell lenniük, mivel a kvarkok esetén egyik feltétel sem teljesül így szabad kvark nem is létezik.

Megjegyzés: A korábbi bejegyzések összefoglalását lásd: „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”

Háromnegyed éve indítottam el „A fizika kalandja” című blogot. Azóta már a félszázadik bejegyzésnél tartok, ezért ideje, hogy összefoglaljam mit tartok a legfontosabbnak írásaimban. Indulásként nézzük meg, hogy mi történt a modern fizika hajnalán.

A fizika XX: századi forradalma

A XX: század fordulóján forradalmi változások következtek be a fizikában, az egyik a speciális és általános relativitáselmélet megjelenése, a másik a kvantumelv, amely az akkor felfedezett parányi fizikai objektumok mozgását értelmezte szokatlan módon. Az előbbi átírta a mechanika törvényeit nagy sebességeknél és korrigálta a gravitáció szabályait, az utóbbi új elveket vezetett be a klasszikus mechanikához képest az atom szerkezetének, az elektronok mozgásának, állapotváltozásainak leírásában.

A relativitáselmélet alkotói

A speciális relativitáselmélet [1]  legfontosabb előzménye Maxwell négy egyenlete volt, amelyben megadta az elektromágnesesség törvényeinek végső alakját, de ne felejtkezzünk el a nagyszerű elődökről sem, akik előkészítették az utat, itt csak a legfontosabbakat felsorolva: Coulomb, Gauss, Faraday és Newton. Lorentz volt, aki felismerte, hogy a Maxwell törvények olyan struktúrával rendelkeznek, amelyek új kapcsolatot teremtenek a tér és idő dimenziói között, ami olyan transzformációs törvényhez vezetett, amelyben a tér és idő koordináták viszonya megváltozott a nagysebességű mozgásokban. Minkowski ezt felismerve vezette be a téridő fogalmát. Az új elmélet általános matematikai megfogalmazását Poincaré adta meg, és Planck volt, aki megfogalmazta a tömeg és energia ekvivalenciáját. Az elmélet végső elveit Einstein fogalmazta meg, akinek nevéhez szokás kötni a relativitáselméletet, de ne feledkezzünk meg az elődökről, akik kitaposták az elmélet megszületéséhez vezető utat.

A speciális relativitáselmélet a mechanika törvényeit egyenletes sebességgel mozgó inercia rendszerekben vizsgálja, de Einstein tovább lépett, amikor gyorsuló rendszerek hatását vizsgálta meg és eljutott a gravitáció eredetének értelmezéséhez a torzult téridő fogalmán keresztül. Gravitációs egyenlete kis korrekciót hozott létre a bolygómozgás törvényében a klasszikus Newton egyenlethez képest, de nem ez adja elméletének jelentőségét, hanem a tér és idő szerkezetének forradalmian új szemlélete. Einstein nem a matematika megfogalmazásokban alkotott nagyot, ő az elvek embere volt, amely lökést adott a fizikának új utak keresésében. Az már tudományos teljesítményének megítélésében is megmutatkozott, hogy a modern fizikában többre becsülik az egyenleteket, mint a fizikai elveket, ezért számára a Nobel díjat nem a relativitáselméletért ítélték oda, hanem a fényelektromos jelenség felfedezésért.

A kvantumfizika megalkotói

A fizika másik forradalmi átalakulása a kvantumelvhez köthető, amit Planck mondott ki, hogy értelmezni lehessen a feketetest sugárzásának törvényét. Ez a démokritoszi atomelv megjelenése volt a fény, az elektromágneses sugárzás értelmezésében. A fényt sem lehet bármeddig kisebb intenzitású sugárzásra bontani, mert eljutunk a fény „atomjához”, a fotonhoz, ami tovább már nem bontható. A kvantumugrás fogalma jelent meg az atomszínképek diszkrét vonalainak értelmezésében, amikor megállapították, hogy az atom elektronjai ugrásszerűen változtatják meg energiájukat. Az első atommodellt még Bohr alkotta meg, aki az elektronmozgást még bolygómozgásként képzelte el és bevezette a stacionárius állapot fogalmát, hogy értelmezze, miért nem sugároz az elektron fényt gyorsuló mozgása során.  A diszkrét változások matematikai értelmezése új módszer bevezetését tette szükségessé, amit aztán Schrödinger és Heisenberg adott meg. Kiinduló elvük az volt, hogy a fizikai mennyiségeket hatásuk alapján kell leírni, ami vagy megtartja, vagy megváltoztatja az elektron állapotát [1, 2,3].. Matematikailag ez azt jelenti, hogy operátorokat használunk, amit függvénnyel szorozva vagy megtartja azt változatlan alakban, vagy más függvénybe viszi át. Ezt két módon valósították meg, Schrödinger differenciál operátorokat vezetett be, míg Heisenberg mátrixokkal reprezentálta a fizikai mennyiségeket. Később kimutatták, hogy a két módszer egyenértékű, és ma a kvantummechanika aszerint választ a két eljárás közül, hogy a konkrét feladat megoldása melyik eljárással kényelmesebb. Ezek az egyenletek még nem tükrözték a speciális relativitáselmélet szabályait, amit aztán Dirac oldott meg, amikor a relativitáselmélet energiaformuláját úgy írta át operátorokkal, ami összhangban volt a szokásos matematikai eljárás követelményeivel [4,5]. Dirac később még továbblépett, amikor megalkotta a kvantumos elektrodinamikát, ahol a Maxwell egyenletek is operátoros formát öltenek, és amelyben egyenrangú szerepet kapnak az elektronok és fotonok, amiket képződő és eltűnő oszcillátorok írnak le. További tudósok is meghatározó szerepet játszottak az elmélet kidolgozásában, mint a kizárási elvet kimondó Pauli, vagy a részecskék statisztikáját leíró Fermi, a részecskék korpuszkuláris és hullámtermészetét összekapcsoló de Broglie és Compton. A felsoroltak Európa különböző nemzeteit képviselték, voltak köztük németek, franciák, angolok, oroszok és olaszok is.

Mesterek és zsenik a fizikában

Talán csak elfogultságomat tükrözi, talán csak ez eltelt közel száz év növeli naggyá múlt század elejének tudósait, de bennük a fizika lángelméit tisztelem, akik döntő hatással voltak a modern fizikára, míg napjainkban inkább csak kiváló mesteremberek művelik a fizika tudományát. A II. világháború előtt még Európa diktálta a fizika fejlődését, a korszakalkotó publikációk is német, angol, orosz, francia, olasz nyelven születtek, ma már azonban mindenütt az USA dominál és alig jelennek meg az angolon kívül más nyelven jelentős publikációk. Ma már a szent „impakt faktor” és a hivatkozások száma határozza meg a tudományos rangot, ezért a magyar nyelvű tudományos publikálás végnapjait éli. Nem kivétel ez alól a blog írója sem, de talán valamit segít, hogy a bejegyzések magyar nyelven felkerülnek fel az internetre. (A szerző publikációinak 700 fölötti impaktja és a ráérkező 3500 hivatkozás elég bizonyíték arra, hogy a tudományos publikáció és értékelés gyakorlatának kritikáját nem a tudományos sikertelenség váltja ki belőlem.)

A kvantumelv diadala a fizikában

A XX. század eleje két fontos tudományos paradigmát vezetett be, az egyik a görbült téridő fogalma, a másik a kvantumelv. A fizikai közgondolkozásban a görbült tér jelentősége a perifériára szorult, száműzték a kozmosz világába, jelentőségét ugyan az ősrobbanás elmélete felismeri [6], fontos a szerepe a csillagok keletkezésében, a szupernóva robbanásokban, a fekete lyukak kialakulásában, de a mikrovilág fizikájában nem kapott lapot. Ennek oka, hogy a gravitáció gyenge az erős és az elektromágneses kölcsönhatáshoz képest, hatása a mikro folyamatokban elhanyagolható. Annál inkább előtérbe kerül a kvantumelv, a modern fizika a mikrovilág jelenségeit kvantumosan írja le, ezt az elvet sikeresen terjesztette ki az elemi objektumokat összekötő és átalakító erős illetve gyenge kölcsönhatás leírására is. Megtorpant azonban, amikor a gravitációt is kvantumokkal akarta leírni, minden erőfeszítés kudarcba fulladt [7]. Ezek lettek napjaink „örökmozgót építő” próbálkozásai. Korábbi évszázadok tanúsága, hogy amikor oly sok erőfeszítés sem tudta megalkotni az örökmozgót, eljött a nagy felismerés pillanata: már pedig örökmozgó nem létezik. Ez lett az alapja a termodinamika tudományának. Talán ma már eljött az idő, hogy felismerjük: a gravitáció nem kvantumos jelenség! Ennek okát már több írásban kifejtettem [8,9], amelynek lényege, hogy a gravitáció nem vezethető vissza fénysebességű forgásokra. Ha a gravitáció nem kvantumos, akkor másképp kell tekinteni a folytonosság és a diszkrét változás hierarchiájára. Nem igaz, hogy a mikrovilágban a kvantumelv kizárólagos. Paradigmaváltásra van szükség! Az a legalsó szint, ami a részecskék belsejébe vezet már folytonos világ, ennek keretében jön létre a fénysebességű forgás, ami a kvantum megszületéséhez vezet. Ez a kvantum viszont eltörpül a makro-világ léptékeihez lépest, és így makroszkopikus törvények már folytonosak lesznek. Hármasléptékű tehát a fizikai világ: ahogy a méretek növekszenek – egy részecske belsejéből elindulva  –  a folytonos átmegy kvantumosba, majd ezután a kvantumos ismét folytonossá válik. Ha így tekintünk a kvantummechanika törvényeire, akkor megszabadulunk a valószínűség és a determinizmus között feszülő dilemmáktól is. A mikrovilágról a kvantumos foton hozza az információt, ezért csak kvantumokban látjuk ezt a világot, a részecskék „sorsát” megszabó sajátforgások fázisa rejtve marad előttünk és emiatt csak a mikrofolyamatok bekövetkezési valószínűsége állapítható meg [2,10,11,12, 13, 14,15,16, 33].

Minden fizikai erő alapja a téridő görbülete [17,18, 19, 20]

A természet legmélyebb világa a folytonosságra épül. A tér és idő nem szakad szét kvantumokra. A fénysebességű forgások extrém torzulást hoznak létre, amikor elvész két dimenzió és létrejönnek a nullafelületű részecskék. De a görbületek tovafutása a részecskék sugarán kívüli tartományba folytonos, és ez érvényes a felületre is, amelyik nulla a felszínen, majd folytonosan növekszik kifelé, amíg eléri az euklideszi geometria által megszabott értéket. Így jön létre legbelül a részecskét egyben tartó erős gravitáció, majd kvarkok esetén a részecske határán egy keskeny tartományban az erős kölcsönhatás, majd attól távolodva a szokásos gravitáció..Elektronok esetén a részecske határon való folytonos átmenetet a kvantumelektrodinamika által bevezetett vákuumingadozás hozza létre. A paradigmaváltás azt jelenti, hogy nem a kvantumokból kell magyarázni a gravitációt, hanem megfordul a kép: minden fizikai erőhatás szülője a tér geometriájának torzulása. Ez vonatkozik az elektromágneses és a gyenge kölcsönhatásra is, mert a kölcsönhatások közvetítő részecskéit is az erős gravitáció alkotja meg [21, 22, 23,24, 25, 26, 30]..

Bekövetkezik-e az új paradigmaváltás?

Vajon mekkora az esély arra, hogy a paradigmaváltás bekövetkezik a fizikai gondolkozásban? Jelenleg nem túl sok. Épp a fizikusok részéről nincs hajlam, hogy kilépjenek megszokott gondolkodási kereteikből. Azt mondják, mi szükség van új elvek megfogalmazására, hiszen csak az a fontos, hogy kísérleteinket jól írják le matematikai egyenleteink, ami ezen túl van az már nem a fizikusok dolga! Kopernikuszra és Galileire hivatkozva kérdezem, vajon mi a fontosabb, hogy a Föld, a Hold és a bolygók pályáját ki tudjuk számítani, vagy az hogy a Föld forog a Nap körül? Elég, ha mindent kiszámítunk és ne akarjuk megérteni, hogy milyen is fizikai világunk?

Milyen megoldatlan kérdésekre válaszol a fénysebességű forgások elve?

A blog több bejegyzésben ismertetett fénysebességű forgás modellel számos olyan kérdésre lehet válaszolni, amit vagy nem válaszol meg kielégítően a modern fizika, vagy a kérdést egyáltalán fel sem veti. Nem tartom kielégitőnek az olyan magyarázatokat, amely csak valamilyen egyenletre hivatkozik, anélkül, hogy az egyenlet fizikai tartalma tisztázva lenne. Csak néhányat sorolok fel a tisztázásra váró kérdések közül, ahol a fénysebességű mozgás hipotézise jó kiindulási pontot ad:

• A spin, azaz a részecskék impulzusnyomatéka hogyan jön létre, ha nem beszélünk forgásról? [1, 8, 10, 17, 27, 28, 32, 33]
• Miért azonos a foton impulzusnyomatéka bármekkora is legyen energiája és frekvenciája? [1,8, 10, 17, 33]
• Miért éppen fele a fermionok impulzusnyomatéka a fotonokénak, miért azonos valamennyi fermion esetén bármekkora is a tömeg? [1, 8, 10]
• A pontszerű elektronnak hogyan lehet impulzus- és mágneses nyomatéka, ha nincs sugara? [1, 8, 10, 20, 27, 32]
• Miért pontosan egyenlő az elemi töltések nagysága minden megfigyelhető elemi részecske esetén? [1,8, 10,  17]
• A nulla nyugalmi tömegű foton esetén hogyan érvényesül a tömeg-energia ekvivalencia törvény? [1,8, 10, 17, 20, 32, 33 ]
• Mi magyarázza, hogy a foton élettartama végtelen, viszont a gyengekölcsönhatás részecskéié rendkívül rövid? [17, 21, 28, 32]
• Miért rövidtávú az erős és a gyenge kölcsönhatás? [17, 21, 23, 32, 62]
• Miért jön létre paritássértés a gyenge kölcsönhatásban és miért nem a többi kölcsönhatásban? [22]
• Miért létezik anyag és antianyag? [1, 10, 29, 63]
• Miért sugárzik szét az anyag, ha antianyaggal találkozik? [10, 17, 18, 23, 29]
• Milyen mechanizmus teszi lehetővé, hogy az univerzumban az anyag domináljon az antianyag felett? [1, 18, 63]
• Miért nem lehet megfigyelni törttöltésű szabad kvarkokat? [21, 25, 29, 32, 35, 38]
• Hogyan magyarázzuk a neutrínó oszcillációt, ha a részecskék fénysebességgel haladnak, tehát nincs nyugalmi tömegük? [17, 25, 26, 29, 32, 37, 62]
• Miért nem ugorhat az elektron negatív energiájú állapotba? [25, 29]
• Hogyan egyeztethető össze a valószínűség a determinizmussal a mikrovilágban? [11, 12, 14, 15, 16, 31, 35, 64]

Megoldatlan kérdések és a természet kényes egyensúlyai

Természetesen sok olyan kérdés van, amire nem tudom a választ. Nem tudom, hogy miért éppen akkorák a különböző kölcsönhatások erőségi arányai, mint amekkorák; vagy mi határozza meg az egyes részecskék tömegének arányát. Ezért csak annyit mondhatok, hogy ezek a téridő szerkezeti paraméterei és rezonanciái [8]. Az viszont nyilvánvaló, hogy az arányok rendkívül fontosak. Legyen egy parányi eltérés a gravitáció törvényében és az univerzum vagy hamar szétrepül, vagy önmagába zuhan; elég egy parányi eltérés az erős, a gyenge és a gravitáció viszonyában és a csillagok vagy be sem gyulladnak, vagy hamar szétrobbannak szupernóvaként; elég egy kis eltérés az erős, a gyenge és az elektromágneses kölcsönhatás arányában és vagy nem jönnek létre a nehéz elemek, vagy hatalmas túlsúlyba kerülnek; legyen csak parányival kisebb, vagy nagyobb az elektron tömege, vagy parányival gyengébb vagy erősebb az elektromágneses erő, és a molekulák könnyebben szétesnek, vagy túlságosan stabilisak lesznek és nem alakulnak át, ami lehetetlenné tenné a biológia folyamatok  alapját képező kémiai reakciók sokaságát. Egész létezésünk, életünk a természeti állandók arányához kötött.[34]

Záró gondolat

A különböző bejegyzésekben bemutatom, hogy valamennyi kérdésre kézenfekvő választ ad a fénysebességű modell. Ez talán elég ok lehet arra, hogy az elgondolást komolyan lehessen venni. Persze tévedhetek, de ha így van, örömmel venném, ha konkrét cáfolatokat kapnék, ha bemutatnák, hogy van jobb magyarázat is a felvetett kérdésekre annál, amit én adok. Ilyen kritikát még nem kaptam, csak olyanokat, ha van nekem már egy „tisztességes” foglalkozásom (egy anyagvizsgáló módszer), akkor miért foglalkozok „ilyesmikkel”? Hát azért, mert szerintem a fizika lényege nem a számítás, nem a matematikai egyenlet, hanem a törekvés, hogy megértsük a fizikai világ  – a valóság – természetét. Ha nem is sikerül elfogadtatni fizikai kalandozásom eredményeit a hivatalos tudomány meghatározó köreivel, akkor is ismételhetem Galilei legendás szavait: „eppur si muove”, mert a spin akkor is forog!

A blog vonatkozó bejegyzései elérhetők a linkre való kattintással, vagy megtalálhatók az Archivumban  hónaponkénti bontásban:

1. Az egységes fizikai világkép (2015, december)
2. Út a kvantummechanika megértéséhez (2015, augusztus)
3. Miért diszkrétek az energianívók kötött állapotban ? (1-5) (2015, augusztus)
4. Fénysebességű forgások és a relativitáselmélet (2015, július)
5. A Dirac-egyenlettől az általános fermion egyenletig (2015, július)
6. Az ősrobbanás és a teremtésmítoszok (2) (2015, november)
7. A modern fizika dilemmái (2015, július)
8. A tér szerkezete és az elemi részecskék mint rezonanciák (2016, január)
9. A tömeg és töltés kettős arculata (2016, január)
10. A kvantumelv határai a fizikában (2016, január)
11. A kvantum logikája (2016, január)
12. A kvantumvilág rejtélyei (1-4) (2016, január)
13. Határozatlansági relációk a kvantummechanikában (2015, augusztus)
14. EPR paradoxon (2015, július)
15. Determinizmus és kvantummechanika: a szabadság szintjei a fizikában (2015, május)
16. Az intelligens elektron (2015, augusztus)
17. A részecskefizika nyitott kérdései (1-2)  (2015, július)
18. Térgörbület és gravitáció forgó rendszerekben  (2015, július)
19. Téridő-részecske  (2015, július)
20. Miért relativisztikusak a fizikai törvények (2015, november)
21. A kvark színe (2016, január)
22. A gyenge kölcsönhatás kiválasztási szabályai és a CPT tükrözés (2015, október)
23. Az elektrogyenge kölcsönhatás és az elemi részecskék átalakulása (1-2) (2015, július)
24. Barangolás a kvarkok és elemi részecskék világában  (2015, október)
25. Nyomozás a sötét anyag után (2015, szeptember)
26. A véges és végtelen az Univerzumban  (2015, október)
27. Az elektron anomális mágneses momentuma (2015, augusztus)
28. Mi a fény (2015, július)
29. Még egyszer a Dirac egyenletről (2016, február)
30. A görbült téridő víziója és a gravitációs hullámok (2016, február)
31. Einstein igazsága és tévedései: Gravitációs hullámok és az EPR paradoxon       (I:  2016, február, II: március)

32. Az elemi részecskék mozgásformái (2016, március)

33. Foton: a mikrovilág postása és szabályozója (2016, március)

34. Hit, tudomány és képünk a világról (2016, április)
35. Fizikai fogalmaink kialakulása és kiteljesedése (2016, április)
36. Szántó Imre: Az élet transzcendenciája (2016, április)
37. Hogyan oszcillálnak a nulla nyugalmi tömegű neutrínók? (2016, június)
38. Miért nem lehet szabad kvarkokat megfigyelni? (2016, június)
39. Csillagközi utazás az Alfa Centaurira (2016, június)
40. Hogyan látogathatjuk meg a legközelebbi csillagokat? (2016 június)
41. Miért kék az ég? Mindennapi fényjelenségek fizikai magyarázata (2016 július)
42. Írjunk magyarul tudományos közleményeket! (2016 július)
43. A fény és anyag kettős természete: hullámok és részecskék (2016 augusztus)
44. A második Föld meghódításának esélye és kockázata (2016, augusztus)
45. Mi a forrása a nyugalmi energiának? (2016, szeptember)
46. Az Univerzum korszakváltásai (2016, szeptember)
47. Hogyan hozhatunk létre teleportálást a kvantummechanika szerint? (2016, szeptember)
48. Dr. Balogh Sándor: Einstein tér/mező kérdésének megoldása c. könyve (2016, október)
49. A valódi és az elképzelt fizikai világ konfliktusa (2016, október)
50. A rejtett paraméterekés a kvantummechanika (2016, október)
51. A gravitáció és az elektromágneses kölcsömhatás párhuzamos története (2016, november)
52. A fizikai világ két arca: A látható és a láthatatlan (2016, november)
53. Rugalmas ütközés: egy lehetséges magyarázat az űrben száguldó nagyenergiájú elektronokra (2016, November)
54. A villám kialakulása (2016, november)
55. Szimmetria jelenségek a mindennapokban és a modern fizikában (2016 november)
56. Hogyan változik a súlyunk utazáskor (2016 december)
57. Rezgések, hullámok és rezonanciák (2016, december)
58. Az a titokzatos alagúteffektus (2016, december)
59. Az elektromágneses sugárzás ezer arca (2017, január)
60. Fontos epizódok a gondolkodás és a fogalmak fejlődéstörténetéből (2017. február)
61. Fekete lyukak a klasszikus gravitációelméletben (2017, március)
62. Látogatás az elemi részecskék szerelőműhelyében: gyengekölcsönhatás (2017, április)
63. Miért dominál az anyag az antianyag felett? (2017, május)

64. A józanész kudarca a modern fizikában (2017, május)

65. Meddig terjed a tudomány szabadsága? (2017, június)
66. Utazás a Föld középpontja felé (2017, június)

67. Volt-e valójában ősrobbanás, vagy a fény sebessége lassul?  (2017, július)

68. Mitől lesz érdekes egy tudományos blog? (2017, július)
69. A Nagy Reccs: összeroppanhat-e az univerzum? (2017, augusztus)
70. Miért vallott kudarcot a fizikusok álma, hogy megalkossák a négy alapvető erő egyesített elméletét (toE) ?
71. Fizika: a világ kulturális öröksége
72. Hogyan gondolkozik az elektron?
73. Hogyan gondolkozik a foton?
74. Mi a foton, részecske vagy hullám?
75. Hogyan igazodhatunk el a mikrovilág útvesztőiben I, II? 
76. Folytonos-e a fizikai világ, vagy kvantumok építik fel? 
77. Kockajátékos-e az Isten?
78. Miért a fémekből lehet jó tükröt készíteni?
79. A valószínűségtől a bizonyosságig
80. A szakértelemig - és tovább
81. Mi a foton: részecske vagy hullám? Egyik se!
82. A kvantumvilág egyik rejtélye: miért hullámtermészetű az anyag?
83. Nemes Ilona: Gondolatjáték a bizonyítás témájában
84. Hogyan kering és pörög az elektron az atomokban?
85. A fizika célja: az állandóság megtalálása a változásban
86. Megfordítható-e az idő iránya?
87. Újabb hírek a Higgs-bozonról
88. Az entrópia szerepe az élet kialakulásában

89. A modern fizika kalandja a virtuális világban

90. Polariton: amikor a fény és az anyag elválaszthatatlanul összefonódik
91. Hogyan hozott létre forradalmat a kémiában egy magyar tudós: Oláh György útja a Nobel-díjhoz
92. Barangolás a valóság és az elképzelt világ határvidékén

93. Szarka László székfoglalójának margójára

94. Elektronok tánca és a kémiai kötés

95. Milyen önarcképet rajzol a foton magáról, amikor a valóságot tükrözi?

96. Hogyan mozognak az elektronok olyan pályákon, ahol nem is mozoghatnának?

97. Az univerzum tágulási és összehúzódási ciklusai

98. A Higgs bozon kérdőjelei
99. Óriások a házban
100. Pillantás az elemi részecskék belsejébe: a kvarkok és gluonok különös világa
101. A pontszerű elektron legendájától a fénysebességű forgásokig
102. A rejtélyes gyenge kölcsönhatás
103. A fénysebességű forgás koncepciója, I. II. és III. rész
104. Ikerparadoxon: A látszat valósága
105. Fizikai alternatívák és matematikai fetisizmus
106. Útikalauz a fizikához: Newtontól Higgsig
107. TV riport kozmológiai kérdésekről
108. Új elmélet  az univerzum keletkezéséről: A Big Bounce
109. A relativitáselmélet leggyakoribb félreértései
110. Specializált szaktudományok és a fizika nagy összefüggései
111. A fizika tér-, idő- és anyagfelfogásának fordulópontjai
112. Mitől lesz a fizika élő tudomány?

113. Az erő- és energiatörvény a látszat és valóság fénytörésében

114. Látszat által elfedett valódi változások a relativitáselméletben

115. Az anyag hullám és részecsketulajdonságainak egyesítése

116. Lohonyai: TEREMTÉSFIZIKA
117. Miben különböznek az elemi részecskék egy kollektív rendszerben, és ez miért vezet szupravezetéshez?

118. A korábbi bejegyzéseket foglalja össze „A fizikai valóság keresése a matematikai formulák mögött”

119. (2015, szeptember) 

     Angol nyelvű bejegyzések:
120. The origin of covariance in the special relativity
121. The intelligent electron
122. The screw model for quantum electrodnamics

Az előző részben („A kvark színe”) a részecskék sajátmozgásait kapcsoltam össze a Standard Modellben összegzett tulajdonságokkal és erőhatásokkal, ebben a folytatásban a kvantummechanika matematikai formalizmusával alapozom meg az elmondottakat.

A mozgási és a nyugalmi tömeg 

A relativitáselmélet a tömeg két típusát különbözteti meg, az egyik a nyugalmi tömeg, ami azt mutatja meg, hogy a fizikai objektum saját rendszerében mekkora ez az érték. A másik a mozgási tömeg, ami a megfigyelt részecskéhez képest állandó sebességgel mozgó inercia rendszerben érvényes. A mozgási tömeg tetszőleges lehet, mert értéke attól függ, hogy éppen mekkora az a sebesség, amivel a részecske a megfigyelőhöz képest mozog, ezt a sebességet ugyanis tetszőlegesen inercia rendszerhez viszonyíthatjuk. A relativisztikus energia a sebességtől függő kinetikus energia és az attól független nyugalmi energia négyzetes összegéből számolható, amit c²-tel osztva kapjuk a teljes mozgási tömeget. 

Az elektron Dirac egyenlete 

Dirac relativisztikus hullámegyenletében a fentiek úgy jelennek meg, hogy egy 2x2 dimenziós mátrixalakban az m₀c² nyugalmi energia a diagonális, az impulzussal arányos relativisztikus  p.c mozgási energia a nem-diagonális pozícióban jelenik meg, másképp fogalmazva az előbbi a diagonális σ_z, az utóbbi a tisztán nem-diagonális σ_x  Pauli mátrixszal van megszorozva, ahol a két Pauli mátrix alakja: 

A diagonális mátrixszerkezetnek alapvető jelentősége van a kvantummechanikai operátorformalizmusban, mert a diagonális elemek felelnek meg az adott fizikai mennyiség mérhető sajátértékeinek. Dirac formalizmusában ezért az impulzustag nem diagonális szerkezete annak felel meg a relativitáselméletben, hogy az impulzus nagysága nem abszolút, hanem attól függ, hogy a tetszőlegesen választott inercia rendszerhez képest a fizikai objektum mekkora sebességgel mozog.

Az általános fermion egyenlet 

 „A Dirac egyenlettől az általános fermion egyenletig” című bejegyzésben vittem tovább Dirac eljárását annak érdekében, hogy tetszőleges elemi fermion (kvarkok és neutrínó) esetén is fel lehessen bontani az energiát nyugalmi és mozgási tagra. Ennek technikája, hogy a Dirac által bevezetett 4x4 dimenziós spinorok helyett 8x8 dimenziós spinorokat alkalmaztam, amelyek viszont felépíthetők három Pauli mátrix direkt szorzataként. Bevezettem a Pauli mátrixból felépíthető diagonális és nem diagonális elemeket egyaránt tartalmazó uniter mátrixot is: 

U_n = σ_z.cosρ + σ_x.sinρ és U^†_n = -σ_z.sinρ + σ_x.cos ρ 

Ez az uniter mátrix kerül a nyugalmi energia együtthatójába σ_z helyébe, míg ennek U^†_n  adjungáltja váltja fel σ_x-et p.c szorzójaként. A ρ szög értéke az n kvantumszámtól függ a cos ρ = n/3 szabály szerint, ahol n = ±3 felel meg az elektronnak és pozitronnak, n = ±2 az u, míg n = ±1 a d kvarknak és végül n = 0 a neutrínónak. Ily módon valamennyi elemi fermion elektromágneses kölcsönhatása egyetlen egyenlettel írható le. 

A tömeg és töltés kvantummechanikai operátora

 Az U_n uniter mátrix egyúttal az e töltés szorzójaként is megjelenik. Az eljárás a kvantummechanikai operátor technika továbbfejlesztését is jelenti, mert ezáltal a tömeg és a töltés is valós szám helyett operátor lesz, melyek definíciója:

m = U_nm   és q = U_ne

Az operátorként kezelt tömeg és töltés azt jelenti, hogy az energiaoperátor által kijelölt állapot határozza meg a két mennyiség várható értékét és annak a hibáját. Ha az m és q operátorok felcserélhetőek az energia operátorával, akkor a részecske tömege és a töltése pontosan megadható. Ez valósul meg az elektron és a pozitron esetében, ezért ezeknek a részecskéknek jól definiált tömege és töltése van, ami pontosan mérhető. A neutrínó képviseli a másik végletet, ekkor az impulzus tag lesz diagonális, míg a töltés és a tömeg tisztán nem-diagonális. Ez vezet oda, hogy a neutrínó töltésének és tömegének várható értéke nulla lesz, viszont impulzusa pontos értékkel rendelkezik. A részecskéket emiatt egy sajátos bizonytalansági reláció jellemzi, ami a relativitáselméletből következik: vagy a nyugalmi tömegük rendelkezik jól definiált értékkel és ekkor impulzusuk a választott inercia rendszertől függ, vagy impulzusuk független az inercia rendszertől, de ekkor a tömeg lesz a választott rendszer függvénye.  Ez feloldja a neutrínó oszcilláció értelmezése körüli zűrzavart. Nem azért létezik három különböző neutrínó, amelyek a kísérletek tanúbizonysága szerint egymásba periodikusan átmennek, mert van nyugalmi tömege a neutrínónak, hanem azért mert rendelkeznek három különböző sajátimpulzussal. Úgy is mondhatjuk, hogy a neutrínó „impulzus típusú”, az elektron és pozitron „tömeg típusú” részecske.

Kvarkok anomális töltése és a renormálási tömeg

A kvarkok külön esetet képviselnek, mert ekkor a tömeg és töltés operátor egyaránt tartalmaz diagonális és nem-diagonális elemeket és ez a helyzet az impulzussal is. Emiatt mind a tömeg és mind a töltés esetén nem az operátorok sajátértéke határozza meg ezeket a mennyiségeket, hanem az állapotfüggvénnyel értelmezett várható érték. Ez a várható érték adja ki a kvarkok anomális ±⅓e és ±⅔e töltéseit. A tömegek esetén is ez a helyzet, a Standard Modellből származtatott renormálási tömegek felelnek meg a várható értékeknek. Szabad kvark viszont azért nem figyelhető meg, mert a részecske nincs sem tömeg, sem impulzus állapotban, és így nem rendelkezik olyan tulajdonsággal, ami a detektáláshoz szükséges..

A tömeg és töltés operátorok fotonok és W bozonok esetén 

Érdemes még arra is rámutatni, hogy a tömeg és töltés operátordefiníciója alkalmazható fotonok esetében is. Ekkor a nulla nyugalmi tömeg és töltés annak felel meg, hogy a tömeg és töltésoperátor egyaránt tisztán nem-diagonális, így a két mennyiség várható értéke nulla lesz. Az impulzus azonban diagonális, ezért pontos értékkel rendelkezik és megadja a teljes energiát, illetve a mozgási tömeget. A gyenge kölcsönhatás W bozonja esetén megfordul a kép, mert ekkor a Pauli mátrix orientációját kijelölő haladási irány merőleges a fénysebességű forgás tengelyére. Ez a formalizmusban úgy jelentkezik, hogy a tömeg és töltés operátor diagonális lesz és így ezek a bozonok jól definiált tömeggel és töltéssel rendelkeznek, más szóval a W bozonok is tömeg típusú részecskék. Az egytengelyű forgások S = 1 állapotai azonban nem teljesen azonosak az S = ½ spinű kettősforgásokkal, ami abban mutatkozik meg, hogy létezik a semleges Z bozon, melyben a két kiralitás együtt szerepel és ekkor eltűnik a töltés, viszont szemben a neutrínóval a tömeg megmarad.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

Előzmények

Az előző részben („Az elemi részecskék mint rezonanciák a téridőben”) foglalkoztam két alapvető részecske típussal, az elektronnal és a fotonnal. Az utóbbi energiája folytonosan változik, az előbbi csak három értéket vehet fel (elektron, müon, tauon), amit a tér rezonanciájához rendeltem, amikor kettősforgás jön létre. Ezek a rezonancia frekvenciák egészítik ki a tér két alapvető állandóját, a fénysebességet és a Planck állandót. Foglalkoztam a két hosszú távú kölcsönhatással is, a gravitációval és az elektromágneses kölcsönhatással, amelyek hatását a tér két újabb állandója határozza meg, az α Sommerfeld finomstruktúra állandó és γ gravitációs állandó. 

Folytonosság – kvantumosság – folytonosság

A gravitáció hatását folytonos függvények írják le szemben az elektromágneses kölcsönhatás által generált kvantumos effektussal. E mögött az a szemléletmód rejlik, hogy a kvantum is csak egy képződménye a téridőnek, amit a fénysebességű elemi forgások hoznak létre. Felfogásom szerint a fizikai világ hármas osztatú: a makrovilágban a folytonos változások jellemzik a törvényeket, amikor eljutunk a mikrovilág határához, már jelentkezik a kvantumok hatása, ezért ekkor a kvantumos leírásra van szükség. De a kvantumvilág mélyén van egy harmadik világ is, ahol újra folytonosnak kell tekinteni a mozgásokat. Ez már az elemi forgások belső világa, amit a forgások fázisa jellemez. A kvantum csupán egy lépcsőfok, ami átvezet az egyik folytonos világból egy másik folytonos világba, és ezt a lépcsőt az erős gravitáció – a tér extrém torzulása – hozza létre, amikor elvész a térből két dimenzió a fénysebességű mozgások miatt. Mivel a mikrovilág hírhozói, a fotonok maguk is elemi forgások, így a mozgások belső fázisáról nincs információnk. Ezt veszi tudomásul a kvantummechanika, amikor eljut a bizonytalansági elvhez. Ez a szemlélet feloldja az ellentmondást, ami a valószínűség és a teljes meghatározottság, azaz a determinizmus között feszül.

A bejegyzés tárgya

Ebben a részben a mikrovilág rövidtávú kölcsönhatásairól, az erős és gyenge kölcsönhatásáról, a kölcsönhatásokat hordozó bozonokról (W, Z és gluonok). valamint a kölcsönhatások alanyairól, a kvarkokról és a neutrínóról lesz szó. Ebben a világban már a kvantum uralkodik, így a kvantumelektrodinamika mellett a két kölcsönhatás leírása is kvantummező elméletek által történik.

A kvarkok tulajdonságai 

A kvarkelmélet jelentős sikere, hogy sikeresen értelmezi a több mint száz mezon és barion, összefoglaló néven hadron létezését. A mezonokat, melyek spinje lehet S = 0, vagy 1, egy kvarkból és egy antikvarkból építi fel a modell, míg a barionok, melyek spinje vagy ½, vagy 3/2, három kvarkot, vagy három antikvarkot tartalmaznak. Az antirészecske töltése ellentétes előjelű a részecskéhez képest.

 Valamennyi kvark spinje ½, amit az elektronhoz hasonlóan kettősforgással lehet értelmezni. A kvarkok különleges tulajdonsága, hogy az elemi töltés törtrészével rendelkeznek, ami lehet ±⅓e és ±⅔e. A ⅔e töltésű kvarkot nevezzük „up” (u), míg a -⅓e töltésű kvarkot „down” (d) részecskének, melyekből a pozitív töltésű proton és a semleges neutron felépíthető, amikor az egyikből kettő, a másikból egy szerepel a nukleon összetételében. Az u és d kvark antirészecskéiből hasonlóan épül fel az antiproton és az antineutron. Az elektron típusú részecskékhez hasonlóan a kvarkoknak is három generációja van, ezek különböző kombinációiból épül fel a mezonok és barionok serege. Erről részletesen írtam már a „Barangolás a kvarkok és elemi részecskék világában” című bejegyzésben.

Miért nem figyelhető meg szabad kvark 

Törttöltésű részecskét, azaz kvarkot azonban semmilyen kísérletben nem lehetett megfigyelni, bármekkora energiával is bombázták a hadronokat (elsősorban a nukleonokat) és ilyet a kozmikus sugárzásban sem találtak. Ezt avval szokás magyarázni, hogy a kvarkokat összetartó erő olyan nagy, amit nem lehet megbontani. Az én értelmezésem szerint azonban másról van szó. Igazában nem arról kell beszélni, hogy két, vagy három kvark „építi fel” a hadronokat, hanem a helyzet fordított: a kettősforgások rezonanciája összetett forgáskombinációkban valósul meg, amelyeknek azonos „mintázata” van, és ezeket az elemi mintázatokat nevezzük kvarkoknak. Tehát a kvarkok a hadronok belsejében létező mozgásformák. Mindegyik önmagában kettősforgásnak felel meg, de a két lehetséges királis kettősforgás együtt van jelen, de súlyuk különbözik. Úgy is mondhatjuk, hogy a királis szimmetriák szuperpozíciója építi fel a kvarkokat. A kvarkok töltését „hatodok” kombinációja hozza létre, így ha ⅚ és ⅙ a két kiralitás súlya megkapjuk a ⅔e töltést, ha viszont 4/6 és 2/6, akkor ⅓e lesz a töltés. Egy korábbi írásban már bemutattam, hogy a Dirac egyenlet általánosításával is eljuthatunk ehhez a képhez. (Lásd: „A Dirac-egyenlettől az általános fermion egyenletig”) 

A kvarkok szín kvantumszáma

A kvarkok rendelkeznek egy olyan kvantumszámmal is, ami csak náluk lép fel, aminek a szakirodalom a „szín” elnevezést adta. Ez természetesen csak egy szimbolikus név, ami onnan származik, hogy ennek a kvantumszámnak három lehetséges értéke van, ahogy összesen három alapszín (kék, vörös és zöld) létezik és ezek keverése létrehozza a fehéret, azaz kvarkok esetén a „szín nélküli” állapotot. Az új kvantumszám bevezetését az tette szükségessé, hogy a Δ⁺⁺delta részecske felépítését három identikus kvark, azaz (uuu) konfigurációval lehetett értelmezni. Fermionok esetén viszont a Pauli kizárási elv szerint minden egyes részecskének különböző állapotban kell lennie, tehát valamilyen kvantumszám alapján különbséget kell tenni közöttük. Elvben a pályaimpulzus kvantumszám szóba jöhetne, de az eredő impulzusmomentum minden barion esetén úgy értelmezhető, hogy ez a kvantumszám nulla. A szín kvantumszám segítségével viszont sikerült valamennyi barion felépítését jól leírni, az összefoglaló kvantumelméletet ezért kvantumkromodinamikának nevezték el.

Vibráció mint a szín-kvantumszám eredete

Fizikai világképemben minden kvantumszám valamilyen sajátmozgáshoz kapcsolódik, így értelmeztem a spint is fénysebességű forgásokkal. Ezért felvetődik a kérdés, hogy milyen belső mozgást végezhet a kvark, ami a szín-kvantumszámhoz vezet. A kvarkot úgy értelmeztem, hogy a két ellentétes kiralitású kettősforgás szuperpozíciója hozza létre. Ez két ellentétes előjelű gömbhéj együttesét jelenti, ahol a héjak felülete nulla, de mindkettőhöz valamilyen véges sugár tartozik. A két héj töltése között vonzóerő lép fel, ami azonban nem csillapodik le, mint az elektromágneses kölcsönhatás esetén, mert a forgási gömbből kilépő fotonok helyett itt közvetlenül hat a Coriolis erő a héjak között. Viszont a kvantummechanika szerint ilyen esetben alapállapotban is vibráció lép fel a komponensek között. Ennek a nullaponti vibrációnak lehet tulajdonítani a szín-kvantumszám létrejöttét, mert a vibráció tengelyiránya a tér három iránya felé mutathat. A képződő hadron a gömbszimmetriát őrzi meg, és csak lokálisan jöhet létre alacsonyabb szimmetria az egyes kvarkokban. A kétkomponensű mezonokban ez azt jelenti, hogy két ellentétes fázisú vibráció kapcsolódik össze, ennek felel meg, hogy a Standard Modell szerint szín és anti-szín kombináció hozza létre a „fehér” struktúrát. A háromkomponensű barionokban viszont mind a három különböző irányú vibráció jelen van, amelyek együttesen gömbszimmetriát alkotnak, azaz a barion „fehér” lesz.

Gluonok az erős kölcsönhatás hordozói 

A kvantumkromodinamika gluonokkal jellemzi a kvarkok közötti vonzó jellegű erős kölcsönhatást, melyek spinje S = 1, szín és anti-szín kombinációk hozzák létre, emellett töltésük is van. Összesen 9 színkombináció épül fel a három-három színből, de ebből a totálszimmetrikust kizárják és így nyolc gluont különböztetnek meg. Ez a sajátmozgás modellben azt jelenti, hogy az x,y és z irányú rezgéskombinációk lépnek fel, amelyben a két különböző vibráció csatolódik össze ellentett fázissal. A kölcsönhatás azért erős, mert a képződő barion belsejében közvetlenül hat a Coriolis erő a csatolt vibrációk között, viszont a hatótávolság rövid, mert a hatás csak a hadron belsejében érvényesül.

A rejtélyes neutrínók 

A neutrínók bujkáló részecskék, mert képződésüket csak közvetve, a megmaradási törvények látszólagos megsértése által lehet kimutatni, ebből következtethetünk arra, hogy mekkora a spinje és mennyi energiát visz magával képződése során. Az erős kölcsönhatás hiánya miatt a neutrínó nem hoz létre összetett fizikai objektumokat, mozgási pályáját nem lehet elektromágneses térrel megváltoztatni, és a pályát sem lehet nyomon követni az ionizációs hatás hiánya miatt. Közvetlen tömegmérésről ezért nem is beszélhetünk, kizárólag képződési idejüket vethetjük össze avval az idővel, amikor a protont átalakítja neutronná. A neutrínó is fermion, spinje ½, elektromos töltése nincs, az is vita tárgya, hogy van-e egyáltalán nyugalmi tömege, mert sebessége a mérési pontosság határán belül a fénysebességgel egyenlő.

A neutrínót olyan kéttős forgásként értelmezhetjük, amelyben a kétféle kiralitás súlya megegyezik és emiatt a Coriolis erő kompenzálódik és nem jön létre töltés. Mivel az erős kölcsönhatáshoz is szükség van Coriolis erőre, így ez a kölcsönhatás is hiányzik. 

 A mikrovilág legáltalánosabb kölcsönhatása

Általános fizikai törvény, hogy minden fizikai objektum megváltozhat, ezért a legáltalánosabb fizikai erő a részecskéket egymásba átalakító gyenge kölcsönhatás. Evvel a kölcsönhatással ezért a neutrínó is rendelkezik és természetesen minden más fermion típusú részecske. A gyenge kölcsönhatás kvantumelmélete a W⁺, W^- és Z kölcsönhatási bozonokkal írja le az átalakulási folyamatokat. Ezek a bozonok S = 1 spinnel rendelkeznek, igen nagy a tömegük, a proton tömegének közel százszorosa és a W bozonoknak töltésük is van, míg a Z bozonnak nincs. Milyen sajátmozgást rendelhetünk ezekhez a bozonokhoz, hogyan értelmezzük a töltésüket, tömegüket és miért csak rövidtávon hatnak miért olyan rövid az élettartamuk? 

Gyenge kölcsönhatás: az elemi részecskék „szerelőműhelye” 

Kiindulópontunk, hogy a spin 1, ami egytengelyű forgások esetén jön létre, viszont minden részecske két fénysebességű mozgás terméke. Foton esetén ez a forgási tengely mentén történő haladó mozgás, ezért ekkor nem támad Coriolis erő. A W részecskék viszont rendelkeznek töltéssel, ami úgy lehet, ha a haladó mozgás iránya merőleges a forgástengelyre, ami létrehozza a ℏ.c/r² nagyságú Coriolis erőt és ezáltal a töltést. A tengelyre merőleges haladás viszont azt jelenti, hogy a forgás sugara fénysebességgel nő, ami fénysebességű forgásnál azt jelenti, hogy az ω = c/r forgási frekvencia ennek ütemében csökkenni fog. Ha a forgási frekvencia csökken, akkor a hozzátartozó ℏ.ω energia is csökkenni fog, ami a részecske gyors eltűnését fogja eredményezni. A frekvencia változása miatt viszont fellép egy új tehetetlenségi erő a Coriolis erőn kívül, amit Euler erőnek nevez a szakmai irodalom és ennek nagysága is ℏ.c/r² lesz, viszont iránya a sugárral lesz párhuzamos. Ez az erő hozza létre a csatolást a W bozon és az átalakítandó, illetve átalakuló részecske között. Az átalakuló részecskék tömege, azaz forgási frekvenciája eltérő, de a bozon épp azáltal, hogy változtatja a frekvenciáját képes szinkronba kerülni bármelyik fermionnal. A távolság, ami a kölcsönhatást jellemzi azonban nagyon rövid, hiszen a fénysebességű tágulás hamar eléri a részecskék sugara által meghatározott értéket. Látható ily módon, hogy a modell nagyon világosan tükrözi a gyenge kölcsönhatás valamennyi tulajdonságait.

Honnan származik a gyönge kölcsönhatási bozonok tömege? 

A gyenge kölcsönhatás további különössége, hogy például a neutron bomlásakor első lépésben a neutron tömegét közel százszorosan meghaladó tömegű bozont hoz létre, ami megsérteni látszik az energiamegmaradás törvényét, legalább is egy nagyon rövid időre. Az erős gravitáció elve azonban erre is választ ad. Amikor létrejön a kölcsönhatási bozon, akkor a tér hirtelen begörbül, ami negatív potenciális energiát hoz létre, ami pontosan fedezi a bozon nyugalmi (azaz kinetikus) energiáját. Voltaképp a szabályos Euklideszi tér nem rendelkezik energiával, de amikor a fénysebességű mozgások által „behorpad” időlegesen szétválik az energia két formája, viszont összegük továbbra is nulla marad. Ez a „horpadás” jelentősen kisimul létrehozva a kisebb energiájú új részecskét. Ezért mondhatjuk, hogy a gyenge kölcsönhatású bozonok „szerelik át” a részecskéket egymásba. Bizonyos részecske átalakulási folyamatok a semleges Z bozon által mennek végbe. Ezt a bozont úgy értelmezhetjük, hogy ekkor a kétféle kiralitású állapot szuperpozíciója jön létre, amikor a Coriolis erő és így a töltés kompenzálódik. 

Gyenge kölcsönhatási bozonok mint a tér rezonanciái 

Miért van az, hogy a foton esetén nem beszélünk nyugalmi tömegről, addig a W és Z bozonok rendelkeznek tömeggel? Ennek oka, hogy a foton nem lokalizálható a tér egy pozíciójában, viszont a W és Z bozonok helye nem változik meg, csak a forgás sugara kitágul. Emiatt a részecske a tér egy adott helyén megtalálható, szemben a száguldó fotonnal, amelynek pozíciója nem lokalizálható. Másik különbség, hogy a foton forgási frekvenciája tetszőleges lehet, míg a gyenge kölcsönhatás bozonjai jól definiált tömeggel, azaz frekvenciával rendelkeznek. Itt hozzá kell tenni, hogy ezek a tömegek és frekvenciák a képződés pillanatában érvényesek és gyorsan lecsökkennek. Ezt azt jelenti, hogy a kezdő frekvencia ismét a tér egy rezonancia sajátsága, amit a sugárirányú mozgás létrejötte követel meg.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

A fénysebesség és a Planck állandó a tér szerkezeti állandói

Amikor az elemi részecskék tulajdonságait és kölcsönhatásait kutatjuk valójában a téridő szerkezetét tárjuk fel. Véges univerzumunkban minden véges, ez vonatkozik a kölcsönhatások sebességére is, ennek határát a c fénysebesség jelöli ki, ami a téridő egyik legfontosabb szerkezeti állandója. Ez a határsebesség hozza létre forgások formájában a részecskék világát és határozza meg a speciális relativitáselmélet mozgástörvényeit. Ezek a törvények viszont arra vezetnek, hogy a fénysebességű forgások extrém mértékben görbítik a teret, mert olyan körpályákat hoznak létre, ahol az r sugárhoz tatozó kör kerülete nulla lesz. A görbült térhez potenciális energia és centripetális erő tartozik, amely fenntartja az elemi, azaz fénysebességű forgásokat a centrifugális erő ellensúlyozásával. Ez a görbületi erő, amit erős gravitációnak neveztem el, a téridő egy második szerkezeti állandójától függ, a ℏ= h/2π Planck-állandótól: F_cp = ℏ.c/r². Az univerzum egységes és ebben a téridő homogén, ami szerint c és ℏ mindenütt azonos, nem csak a Földön, a Naprendszerben, a Tejútrendszerben, hanem a távoli galaxisokban is, és emiatt lesz azonos valamennyi elemi részecske bárhol is legyen.

A foton fénysebességű mozgásai

A részecskék közül egyedül a foton rendelkezik avval a tulajdonsággal, hogy energiája tetszőleges lehet. A foton egytengelyű forgás, amely egyidejűleg a forgástengely irányában szintén fénysebességgel halad és a forgás frekvenciája tetszőleges lehet. Ez az ω = 2π.ν frekvencia határozza meg a foton energiáját E = h. ν  = ℏ.ω  , illetve impulzusát P = h. ν/c összefüggések szerint. Az erős gravitáció kifejezéséből az is következik, hogy a foton impulzusnyomatéka  I = ℏ független a foton frekvenciájától, ennek felel meg a foton S = 1 spinje, ami a Planck állandó együtthatója az impulzusnyomaték kifejezésében.

Az elektron sajátforgásai : a fénysebességű kettős forgás

A fotont S = 1 spinje miatt mint bozont kategorizálja a részecske fizika. Ezzel szemben azok a részecskék, mint az elektron, pozitron, neutrínó, proton fele akkora impulzusnyomatékkal rendelkeznek, azaz S = ½ a spin, a fermionok osztályába tartoznak. A spin feleződését avval magyarázzuk, hogy ezek a részecskék kettős forgást végeznek, egyfelől ugyanúgy fénysebességgel forognak, mint a foton, de ekkor a forgástengely is forog és a két forgás együtt egy gömbfelületen történik. A kettősforgás megduplázza a centrifugális erőt, amit csak úgy tud kompenzálni a tér görbületi ereje, hogy fele akkora impulzusnyomatékot hoz létre. Szemben a fotonnal, amelyik fénysebességgel halad és ezért nem lokalizálható egyetlen pontban és emiatt nem is beszélhetünk nyugalmi tömegről, a fermionok gömbje kijelöl egy matematikai pontot, ami már lokalizálja a tömeget is. További eltérés a fotonhoz képest, hogy a két forgás miatt fellép egy tehetetlenségi erő, amit Coriolis erőnek hívunk, ez egy csavaró hatást hoz létre, melynek nagysága szintén F_Coriolis = ℏ.c/r², viszont a csavaró hatásnak két iránya lehet, attól függően, hogy a két forgás hogyan csatlakozik egymáshoz képest. Ezt a két lehetőséget a jobb- és balkéz szimmetriájához rendelhetjük, amit egyébként kiralitásnak nevezünk. Foton esetén ez a tehetetlenségi erő nem lép fel, mert ott a forgás tengelye és a haladás iránya párhuzamos. Ez magyarázza, hogy a foton nem rendelkezik elektromos töltéssel szemben az elektronnal és a pozitronnal. Az elektront tekintjük anyagnak, a pozitront antianyagnak, ami annak felel meg, hogy az egyik részecske jobbkéz, a másik balkéz szimmetriával rendelkezik. A Coriolis erő két ellentétes csavarási iránya okozza, hogy ez elektromos töltés előjele ellentétes az elektron és a pozitron esetén.

A téridő négy dimenziójának kapcsolata a fizikai mennyiségeket meghatározó három dimenzióval

Fizikai dimenziókról két értelemben szokás beszélni, az egyik a téridő négy dimenziója (háromdimenziós tér plusz az idő), a másik a fizikai mennyiségek három dimenziója: a hossz, az idő és a tömeg. A kétféle dimenziós elv között természetes kapcsolatot teremt a fénysebességű mozgásokon alapuló részecskemodell, ami a téridő-részecske fogalomhoz vezet. Mivel kétféle fénysebességű mozgás szükséges a részecskék felépítéséhez ez két térdimenzió elvesztését jelenti, ami azonban létre hoz egy újat, a tömeget. Így alakul át a téridő négy dimenziója a részecskék saját tulajdonságait leíró három dimenzióvá.

A részecskék mint a tér rezonanciái

A dimenziók természetes alapegységéül a téridő állandói választhatók, így a c fénysebesség és a h Planck állandó, de hiányzik a harmadik természetes állandó. Erre legesélyesebb az elektron tömege, mert ez az egyetlen olyan stabilis részecske, amelyik nem összetett, mint a proton, hanem valóban eleminek tekinthető. Felmerül a kérdés, hogy szemben az egytengelyű forgásokkal, tehát a fotonokkal, ahol tetszőleges forgási frekvencia megengedett a kétdimenziós forgások miért csak diszkrét értékeket vehetnek fel, ami elektron és pozitron esetén 0,511 MeV, a vele hasonló tulajdonságú μ  (müon) és τ  (tauon) részecskék esetén 105,7 MeV, illetve 1777 MeV nyugalmi energiának felel meg. Az utóbbi két részecske azonban nem stabilis 2,2.10^-6 s illetve 3.10^-13 s felezési idővel bomlik el a gyenge kölcsönhatás mechanizmusában, miközben elektronok és a semleges neutrínók képződnek. Az említett részecske család, amit a szakirodalom a leptonok közé sorol, úgy képződik, hogy a kettős forgás során a kétféle forgás rezonanciába kerül. Az alaprezonancia hozza létre az elektront, a magasabb frekvenciájú rezonanciák a müonnak és tauonnak felelnek meg. Az utóbbiak tehát az elektron gerjesztett állapotai. Jelenlegi elméleti modellek, például a Standard Modell nem ad választ arra, hogy miért pont ekkorák a részecske tömegek, illetve rezonancia frekvenciák, ezért csak annyit mondhatunk, hogy ez a téridő még feltáratlan szerkezeti tulajdonsága. Még az is kérdéses, hogy csak ez a három rezonanciaállapot (generáció) létezik, vagy lehet-e egy nagyobb energiájú (3000 MeV fölötti) és még rövidebb (például 10^-20 s) felezési idejű gerjesztett állapot is. A jelenlegi elméleti modellek más részecskecsaládokban, így a neutrínóknál és kvarkoknál sem látják szükségesnek a negyedik generáció létezését, de ennek lehetősége ott is megvan.

A kölcsönhatások csatolási állandói

A tér szerkezetéről nyerünk információt a különböző kölcsönhatások alapján. Két hosszú távú kölcsönhatás létezik, az egyik a gravitáció, a másik az elektromágneses. Közös bennük, hogy az erőhatások a távolság négyzetével csökkennek és mindkettőre a c sebességű terjedés vonatkozik. Ebből arra következtethetünk, hogy mindkét esetben a részecske saját mozgása által perturbálja a környezetét valamilyen „külső” mozgás indukálásával, ami aztán gömbszerűen terjed a térben és azért gyengül, mert a forrástól távolodva nagyobb felületen oszlik el és így az erő a sugár négyzetével arányosan lecsökken.

Az elektromágneses kölcsönhatás kvantumelmélete

Az elektromágneses kölcsönhatásra kvantumelektrodinamika jó leírást ad, aminek lényege a részecske körül az elektromágneses mező létrehozása virtuális fotonok kibocsátása és elnyelése révén. (A virtualitás azt jelenti, hogy ezeket a fotonokat közvetlenül nem „látjuk”, viszont hatásuk hozza létre az elektromos mezőt.) A kibocsátások és elnyelések dinamikus egyensúlya biztosítja az erőmező statikus jellegét, azonban ennek értéke ingadozik az átlagérték körül. Ezt a jelenséget nevezik vákuumingadozásnak. Az elmélet legfontosabb sikere, hogy az ingadozás révén lehetett magyarázatot adni két fontos kísérleti megfigyelésre, az egyik az elektron anomális mágneses nyomatéka, a másik a Lamb shift. Az utóbbi jelenség bizonyos degenerált (azonos értékű) elektron nívók felhasadását magyarázza, ami még a relativisztikus Dirac egyenlet szerint is azonos energiájú. A mágneses nyomaték anomáliája azt jelenti, hogy a kísérletileg meghatározott érték eltér a Dirac egyenlet alapján várttól. Az elmélet összhangban van a fénysebességű forgásmodellel, mert az elektromos mező arányos a kettősforgás Coriolis erejével: E = αℏ.c/r²  (Itt a szimbólum vastagítása jelzi, hogy nem energiáról van szó!). Az elektromos mező kifejezésében az  α = 1/137 a Sommerfeld féle finom-kölcsönhatási állandó úgy értelmezhető, mint a kettősforgás és az egytengelyű forgás csatolási állandója, mely szerint a csavaró erőnek csak egy kis hányada hoz létre, vagy nyel el egytengelyű forgásokat, azaz virtuális fotonokat. Miért pont ekkora az állandó? Erre nincs elfogadott magyarázat, ezt is úgy tekinthetjük mint a tér szerkezeti állandóját, ami meghatározza két különböző mozgásforma csatolódását. Az elektromágneses kölcsönhatás kvantumos, mert a virtuális fotonok is rendelkeznek S = 1 spinnel, ami a kvantum alapja.

A gravitációs kölcsönhatás és a Kepler forgások

Az elektromágneses kölcsönhatásnál még azt kell kiemelni, hogy nem függ a részecske tömegétől, azaz a sajátforgás frekvenciájától. Ebben a tekintetben nagy a különbség a tömegvonzáshoz képest, amelynek ereje arányos az m tömeggel, tehát a részecske ω sajátfrekvenciájával. Ezt úgy értelmezzük, hogy a tömeg –  tehát a kettősforgás – a részecske környezetében lassú frekvenciájú kettős forgásokat gerjeszt, amelynek frekvenciája a Kepler törvény szerint változik, azaz γ.m = Ω²R³, ahol  γ az általános gravitációs állandó, Ω a keringés frekvenciája és R a sugara. Kiindulva ebből a feltevésből és számításba véve, hogy ez a keringés mennyivel csökkenti a pálya kerületét a speciális relativitás elmélete szerint, majd ez alapján definiáljuk a tér görbületét, ami aztán elvezet Newton tömegvonzási törvényéhez (Lásd a korábbi bejegyzésekben: „Fénysebességű forgások és a relativitáselmélet”). Ez az elgondolás alátámasztja, hogy a részecske sajátforgása valóban úgy perturbálja környezetét, hogy kialakulnak a tömeg körül a lassú Kepler forgások. Fejezzük ki a részecske tömegét a sajátfrekvenciával: m = ℏω/c² és rendezzük át az egyenletet:

A kifejezésben szereplő γℏ/c² a gravitációs kölcsönhatás csatolási állandója, ez a tér egy további szerkezeti állandója, aminek értékére nincs elméleti magyarázat. A Kepler forgás frekvenciájának négyzete arányos a részecske saját frekvenciájával. Mivel a görbület Ω² –tel arányos, így mindig pozitív lesz, ezért a gravitációs hatás összeadódik függetlenül a részecske kiralitásától. Ez is különbséget jelent az elektromágneses kölcsönhatáshoz képest, ahol vonzó és taszító kölcsönhatás egyaránt lehet. Nullához tartó sugár esetén a Kepler frekvencia végtelen lenne, de ez nem fordulhat elő, mert a Kepler forgások a részecskén kívüli tartományban jönnek létre. Nézzük meg, hogy mekkora lesz a Kepler frekvencia közvetlenül a részecske felületén, amikor R = r = c/ω? Az eredmény:

ahol a Planck idő definíciója:

A Planck idő rendkívül rövid (~10^-43 s), ezért a Kepler frekvencia és a hozzá tartozó kerületi sebesség annyival kisebb a fénysebességnél, hogy a részecskéből kilépő tartományban a relativisztikus rövidülés elhanyagolható. Mivel a tömeg létrejöttét a fénysebességű mozgás idézi elő a Kepler forgáshoz nem rendelhető tömeg és emiatt impulzusnyomaték sem. Spin hiányában viszont ezek a forgások nem kvantumosak. Ez magyarázza, hogy miért nem lehet a gravitációra kvantumelméletet alkotni.

Mi közvetíti a térben a gravitációs hatást?

Összevetve az elektromágneses és a gravitációs hatást kiváltó mechanizmust, az előbbire világos magyarázatot ad a kettősforgás Coriolis ereje, amely útjára indítja a virtuális fotonokat, de milyen erő okozhatja a szintén fénysebességgel terjedő gravitációs hatást? A szokásos fizikai közegekben, vízben vagy a levegőben, ha egy lokális forgás, azaz örvény jön létre, az környezetében hullámokat vet, de ebben az esetben a közeget alkotó objektumok ütközése hozza létre azt a kölcsönhatást, amely közvetíti a hullámok terjedését. Ilyenkor beszélhetünk a közeg viszkozitásáról, de jogos-e feltételezni hasonlót a vákuumban? A fénysebességű kettősforgás tartományának határfelületén – azaz az r = c/ω  sugárnál – a felület nulla, azon kívül, ha nem lenne Kepler forgás azonnal 4r²π   értékre ugrana fel a felszín, tehát egy végtelenül éles ugrás következne be a tér szerkezetében. Matematikailag ez egy szakadást jelentene a felszín sugártól való függésében. Ez már egy kvantumos ugrást jelent, ami realizálódik is az elektromágneses kölcsönhatásban, ami elvezet a kvantumelektrodinamika formalizmusához. A gravitáció viszont folytonosságot követel meg, nincsenek kvantumai. Ez abban nyilvánul meg, hogy a határon való átlépés függvénye kissé „lekerekedik”, a felszín sugártól való függése differenciálhatóvá válik. Másképp fogalmazva: a tér szerkezete nem engedi meg a végtelenül éles ugrásokat, az ugrás élességének is van egy felső határa. Ez a határ a tér szerkezeti tulajdonsága, aminek mértékét a γ gravitációs állandó határozza meg. A forgási frekvencia szempontjából ez úgy mutatkozik meg, hogy az ω sajátfrekvencia az r = c/ω  határt átlépve nem nullára esik le, hanem az Ω  Kepler frekvenciára, amelynek nagysága a Planck idővel megadott mértékben kapcsolódik a sajátforgás frekvenciájának négyzetéhez. Ez a forgás virtuális, hasonlóan az elektromágneses kölcsönhatást közvetítő fotonok virtualitásához, szerepe hogy a térben továbbterjedve felépítse a teljes gravitációs mezőt.

Az erős kölcsönhatás és a tér görbülete

A tér görbületének folytonossága a részecskék környezetében nem csak azt követeli meg, hogy a görbület ne nullára essen le, hanem azt is, hogy az átmenet folytonos legyen. A felszín szempontjából ez azt jelenti, hogy a részecske nulla felszíne fokozatosan veszi fel a 4r²π értéket egy nagyon keskeny átmeneti tartományban..Ennek megnyilvánulása kvarkok esetén, hogy ezek a részecskék nem rendelkeznek határozott tömeggel és ennek megfelelően a sugár nagysága sem meghatározott. A sugár határozatlansága pedig a térgörbület határozatlanságát hozza magával. Ez a görbületi eloszlás lesz a kvantumos  és rövidtávon ható erős kölcsönhatás forrása.  A folytonosság elve elektronok és pozitronok esetén a kvantumelektrodinamika által bevezetett vákuumingadozásban jelenik meg, amely térgörbületi eloszlást hoz létre a részecskék határán.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

A kvantumvilág értelmezési problémáival már több bejegyzésben is foglalkoztam. Itt most arra a kérdésre térek ki, hogy egyeztethető össze a kvantummechanika fogalomvilága a formális logika szabályaival.

A formális logika alapelvei

A logika három alapelvét, axiómáját lehet megkülönböztetni.

1. Az identitás szabálya: Az „ A” állítás egyenlő A-val.
2. Ellentmondás mentesség: Az „A” állítás nem lehet egyenlő „A” tagadásával
3. A „H” harmadik kizárásának elve: A „H” állítás nem lehet egyidejűleg azonos „A”-val és ’A” tagadásával.

Szemléltessük a három szabályt egy egyszerű példával: 1. A fehér azonos a fehérrel, 2. A fehér nem azonos a feketével, 3. A szín nem lehet egyszerre fehér is, meg fekete is.

Logikai elvek a klasszikus és kvantumfizikában

A klasszikus fizikában ezek a logikai elvek maradéktalanul érvényesülnek, de nem úgy a kvantummechanikában. Nézzük például a harmadik kizárásának elvét. A kvantummechanika szerint a részecske egyidejűleg rendelkezik hullám és korpuszkula természettel, vagy vegyünk egy másik példát: a hullámfüggvény szerint az elektron egyidejűleg a molekula több helyén is tartózkodik bizonyos valószínűséggel. A valószínűség koncepció ellentmondani látszik a szabállyal, hiszen e-szerint lehet az elektron itt is, meg ott is.

A kvantumlogika alapvetése

A kvantumlogika tehát újféle gondolkozás kíván? Van is ilyen próbálkozás, amire példa Peirce („Values in a Universe of Chance, Selected Writings of Charles S. Peirce”, New York, Dover Publications, 1966), felvetése a kvantumok logikájáról. Ebben a kizárási szabályt a „beleértés” szabálya helyettesíti, ami nem a „vagy-vagy”, hanem az „is-is” logikájára épül.

Az elektron egy molekulában

Az „is-is” logika szemléltetésére gondoljunk végig egy konkrét példát, legyen ez a benzol molekula. Ez a molekula 6 szén és 6 hidrogén atomból épül fel, ahol a hat szén egy szabályos hatszöget alkot és minden egyes szénhez a hatszög síkjában egy-egy hidrogén kapcsolódik. Ez a szerkezet nem csupán matematikai absztrakció, mert a nagyműszeres mérési technika által láthatóvá is tehető. A kvantummechanikai számítások az elektronokat „molekulapályákon” helyezik el. Ezek a pályák atomi pályákból épülnek fel, ahol a valószínűségi amplitúdók határozzák meg az egyes atomi pályák részvételi súlyát. Ez úgy értelmezhető, hogy az elektron különböző atomokon egyidejűleg van jelen. Nézzük például a síkra merőleges un. pi kötéseket. Ezek olyan pályát alkotnak, amelyben egyenlő súllyal szerepelnek a sík fölött és alatt rész, de magában a síkban az elektron nem fordulhat elő, azaz nem közlekedhetnek az elektronok a sík alatti és fölötti tartományban, mégis egyszerre jelen vannak mind a két helyen. Az elektron viszont oszthatatlan egész, tehát ténylegesen egyidejűleg van jelen különböző helyeken.

Hogyan teljesíti az elektron a harmadik logikai szabályt?

 Ez ellenkezik a harmadik logikai szabállyal, mert egyszerre van itt is, meg ott is. De ez csak akkor igaz, ha az „ott” az „itt” tagadása. Hogyan tudjuk az „itt” fogalmát megkülönböztetni az „ott”-tól? Ha a molekulákat kirakjuk egy golyókból és pálcikákból álló modellből és ezt az asztalra tesszük, akkor könnyű megkülönböztetni a sík alatti és feletti oldalt. Az egyik az asztalon nyugszik, a másik fölötte van. De hogyan különböztethető meg a benzol molekulában, hogy mi van az egyik és a másik oldalán? Ezt elvben megtehetjük, ha egy fémion kötünk az egyik oldalára, ekkor ez a fémion fogja játszani az „asztal” szerepét. Mit mond ilyenkor a kvantummechanika? Ekkor olyan molekulapályákat alakít ki, amelyik eltérő valószínűségeket rendel a molekula két oldalára. A hangsúly a megkülönböztethetőségen van, ez pedig a fizikában valamilyen eltérő típusú kölcsönhatást jelent. Ha két térrészben teljesen azonos kölcsönhatások vannak, akkor nincs értelme két különböző térrészről beszélni. Akkor a kettő egy és ugyanaz!  Mondhatjuk, hogy ekkor az „itt” és az „ott” azonos. Ezt fordítja le a kvantummechanika a valószínűség nyelvére. Más szóval a kvantummechanika az a nyelv, ami figyelembe veszi, hogy az információk korlátozottsága miatt a térről szerzett fogalmaink eltérnek a mikro- és a makro világban.

Az információ forrása a foton

A mikrovilágból érkező információ fénykvantumokon át érkezik el hozzánk. Ez az információ nem az elektronpálya egyes pontjaiból jut el hozzánk, hanem a pályák egészéről, pontosabban arról a két pályáról, ami között az elektron ugrást végez foton kibocsátása mellett. Tehát a foton nem egyes térbeli pontokról ad hírt, hanem az elektronpálya egészéről. Az elektronpálya pedig azt mutatja meg, hogy a kölcsönhatási terében mekkora a valószínűsége, hogy az elektron itt vagy ott tartózkodik.

Az elektron hullám és korpuszkuláris jellege

Hogyan értelmezzük az elektron hullám és korpuszkuláris természetét? Az elektron pályák leírásánál egy feltételhalmazból indulunk ki. Feltételezzük, hogy az elektron a benzol molekulában hat szén és hat hidrogén atomaggal, valamint a többi elektronnal van kölcsönhatásban. A feltételezett kölcsönhatási rendszerben keressük az energiaminimumot, ami elvezet megfelelő matematikai eljárások révén egy molekulaszerkezethez, ami kijelöli az atommagok helyét és az elektronpályákat. Ebben a fázisban tehát csak feltételezett kölcsönhatási rendszerről van szó és az elektron eloszlását egy hullámfüggvény írja le. Ez tehát a hullámtermészethez tartozó leírás. De most bombázzuk a molekulát jól pozícionált gammasugárzással, ami valahonnan kilök egy elektront. Ez a valódi kölcsönhatás már a korpuszkuláris jellegről ad számunkra felvilágosítást. Tehát a hullámtermészet tartozik a feltételezett és korlátozott információk birodalmához, amikor abból indulunk ki, hogy az elektron ott van valahol a molekulában, a korpuszkuláris sajátság meg akkor mutatkozik meg, amikor egy konkrét kölcsönhatáson keresztül konkrét információhoz jutunk. Ez a kétféle információs szint vezet ahhoz, hogy az elektron hullám is, és korpuszkula is. Tehát a korpuszkula kép nem tagadása a hullámtermészetnek, hiszen nem azonos információs rendszerben mutatkozik meg a kétféle viselkedés.

Összefoglaló értékelés

A kvantumlogika és a szokásos formál logika feloldását én nem abban keresem, hogy a logikai alapszabályait kell átírni, hanem az egymást kizáró ellentétpárokat kell szemügyre venni, vajon tényleg a „vagy-vagy”, tehát a teljes kizárás valósul meg, vagy van helye van a megengedő „is-is” megközelítésnek is. A mikrovilágból nyert információk mindig a teljes elektronpályákra vonatkoznak, emiatt az „itt” és „ott” ellentétpárja elmosódik, többé nem egymást kizáró fogalmak, és ezt írja le a kvantummechanika a valószínűségi amplitúdók, azaz a hullámfüggvény bevezetésével. Ebből fakad a bizonytalansági elv is, mert a makroszkopikus világban kialakított térfogalmaink nem abszolútak, csak részben érvényesek a mikrovilágban. Ez érvényes akkor is, amikor a hullám és korpuszkula természet alternatívájáról beszélünk, ha a tér nem abszolút, akkor a benne megvalósuló részecskepályák leírása sem vágható szét egymást kizáró ellentétpárokra. Ezt egészíti ki az információs szint eltérése is, amikor a részecske pályáját a kölcsönhatás előtti állapotban összevetjük a kölcsönhatásban megvalósuló állapottal. Ez magyarázza meg azt, amit az szakmai irodalom a hullámfüggvény redukciójaként ír le.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.