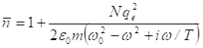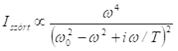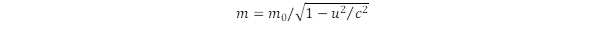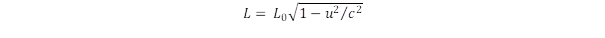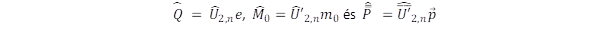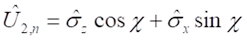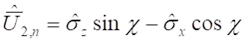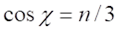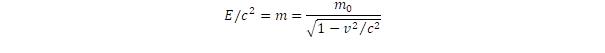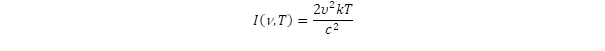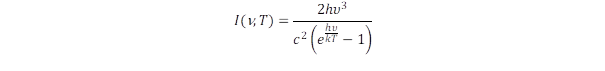A hétköznapi fogalmak kialakulása
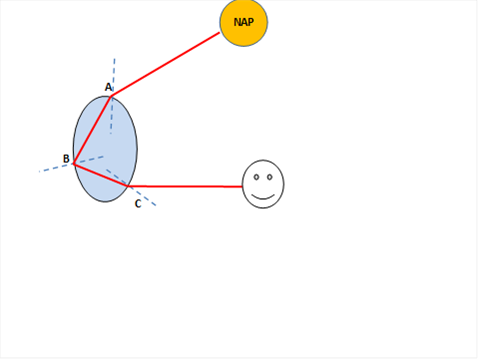
Nincs annál nehezebb, mint kilépni megszokott hétköznapi fogalmaink világából, pedig erre van szükség, ha érteni akarjuk a mikrovilág folyamatait. Tegyünk erre kísérletet! Kiindulási pontunk, hogyan alakultak ki a térről és időről fogalmaink? Környezetünkből számtalan információ ér minket minden pillanatban, ha elég „világos” van, akkor ezek közül a legfontosabbak a fotonok. A szemünkbe érkező fotonok az optikai lencse leképzési szabályai alapján vetítődnek a sárga foltra, ahol bonyolult kémiai folyamatok útján jutnak el különböző idegpályákra, ami elviszi többszörös átalakítás után az információt az agyba, ami aztán „képpé” dolgozza fel a befutott óriási mennyiségű információt. Ebben a rendkívül összetett folyamatban összehasonlításra kerül, hogy milyen irányból, milyen távolságból, mekkora intenzitással és milyen frekvenciában (színben) érkeztek a fotonok. Mindezt a nagy munkát az agy rendkívül gyorsan, tudatunk bekapcsolása nélkül reflexszerűen végzi el. Az agy megkülönbözteti és sorba rakja az egymást követő képeket és kialakítja bennünk a mozgás képzetét is.
Az emberi tudat azonban elvégzi az információ másodlagos – tudatos – feldolgozását is, amikor felépíti a maga fogalmi rendszerét. Ezek rendszerező elvek, mint az irány, a távolság, az intenzitás, vagy a szín, de beszélhetünk a „képek” egymásutániságáról is bevezetve az előbb és az utóbb fogalmát, és ezek alapján jutunk el olyan absztrakt fogalmakhoz is, mint a tér és az idő és a kettő összekapcsolásához, amit mozgásnak és változásnak nevezünk el. Ha a változás ellentétét akarjuk megnevezni, akkor beszélünk az állandóságról. A tér kiterjedésének jellemzésére eljutunk a dimenzió fogalmához, aminek három összetevője van, a hosszúság, a szélesség és a magasság, és amikor ezt a három kiterjedést egybe foglaljuk, előkerül a vektor fogalma is. E a fogalomrendszer segít, hogy beszéljünk és gondolkozzunk a minket környező világról, és tudatunkban újra felépítsük azt. Így jutunk el a képzelet világához is, ami eredetét tekintve a valódi világból származik, de már jelentős átalakuláson megy át. Ez a világ már nem csak az, ami minket körül vesz, ebben már benne vagyunk saját magunk is, tükrözi vágyainkat és reményeinket is. Ez már egy szubjektív világ.
A logika törvényei
A tudat világának következő szintje, amikor „érteni” akarja a külvilág eseményeinek kapcsolatát, amikor felveti a miért kérdését és keresi az egymást követő események közötti oksági kapcsolatot és eljut végül a törvény fogalmához. A törvényen már olyan szabályszerűséget ért, ami tőle függetlenül is létezik, és ami előrelátható következményekkel jár, ami alapjában determinisztikus és megfigyelésekkel megismerhető (elvben a stochasztikus folyamatok – ahol a komponensek rendkívül nagy száma miatt valószínűségi változókat használunk – is visszavezethetők determinisztikus lépésekre). Kialakul a ráció és a logika rendszere, a racionális gondolkozás eszközei. A megismerés folyamata szisztematikussá is tehető, ami elvezet a tudomány kialakulásához is.
A tudomány fogalomrendszere
A tudomány is kialakítja a maga fogalomrendszerét, ami a szétválasztáson és az összehasonlításon alapul. A szétválasztás azt jelenti, hogy csak nagyon elszigetelt jelenségeket tanulmányoz és elhanyagolhatónak tekinti az egyébként mindig létező kölcsönhatások sokaságát. A tudomány eszköze és nyelve a matematika, ami a fogalomalkotás további absztrakcióját jelenti, de ezt nem szakadhat el a mögöttes valóságtól. Alapvető ezért az egyenletek mögött húzódó valóságkép megrajzolása, ami különösen fontos a mikrovilágban, ahol a kvantummechanika törvényei adják a megfelelő leírást. Ezt a kérdést már korábbiakban is feszegettem, de fontosnak tartom ezt újra elővenni.
A klasszikus pályafogalom
A fizika is átveszi mindennapjaink fogalomrendszerét a térről, időről és a mozgásról. Akár egy labda pályáját követjük, akár megfigyeljük az égen a csillagok és a bolygók mozgását folytonosan nagyszámú foton érkezük szemünkbe, ezért a térről és időről alkotott képünk is a folytonosságon nyugszik. A folytonosság kapcsolatot teremt a mozgó test térbeli helye és az idő között, és ezt a kapcsolatot függvény fogalmával jellemezzük. A számok világában erre a folytonossági elvre épül a matematikai analízis, amikor bevezeti a differenciálhányadosok fogalmát, ami aztán alapul szolgál, hogy a mozgást leírjuk a sebességgel és annak változásával, a gyorsulással.
A newtoni mechanika fogalmai
Vegyük most szemügyre a newtoni mechanika fogalomrendszerét. Ebben olyan fogalmakkal találkozunk mint impulzus, erő és energia, amely fogalmak matematikai relációba hozhatók a tömeggel, sebességgel és a gyorsulással. Az utóbbi két fogalomról már volt szó, de milyen hétköznapi fogalmunk van a tömegről? Alapjába véve a tömeget súlya alapján értelmezzük, azt mondjuk az egyes tárgyakról, hogy milyen „nehéz”. A medicinlabda például nehezebb, mint a futball labda, ennél viszont könnyebb a teniszlabda és még könnyebb a pingpong labda. Ezt a megfigyelést tudjuk összehasonlíthatóvá tenni a „mérleg elv” segítségével, ha megállapodunk valamilyen egységet alkotó súly használatában.
A testek súlyát azáltal érzékeljük, hogy nagyobb erőt kell kifejteni a medicinlabda felemelése és kézben tartásához, mint amikor ugyanezt tesszük a futball labdával. De ezzel már önkéntelenül is bekapcsolunk egy újabb fogalmat, az erőt! De mi az erő? Erőt fejtünk ki nem csak akkor, amikor a labdát a kezünkben tartjuk, hanem akkor is, amikor eldobjuk, azaz mozgásba hozzuk. Ilyenkor a labda nyugvó helyzetét megváltoztatjuk, ami sebességváltozással, azaz gyorsulással jár együtt. Ezt fejezi ki Newton második törvénye, amikor azt mondja ki, hogy az erő a tömeg és a gyorsulás szorzata. A tömeg fogalma itt elválik a „súly” fogalmától, ez már a test tehetetlenségének mértékét fejezi ki: minél nagyobb a tömeg – azaz minél nehezebb – annál nagyobb erőt kell kifejteni, hogy a test gyorsulása ugyanakkora legyen.
A tömeg fogalmának továbbépítése is Newton nevéhez kapcsolódik, amikor felismerte, hogy ugyanaz az erő hozza létre a Földön a testek súlyát, mint ami a bolygókat a Nap körüli pályán mozgatja, ez a gravitáció törvénye. Ebben a törvényben a tömeg egyaránt tárgya és létrehozója az erőnek.
A mozgás állandói
Más irányú szerepét mutatja a tömegnek, amikor golyók, vagy más objektumok ütköznek, ez a jelenség a mozgás hatásától, más szóval az impulzustól függ, amit a sebesség és a tömeg szorzata ad meg. Ebből adódik, hogy a változatlan sebességű mozgást az impulzus állandósága tartja fent. De a változó sebességű mozgások összehasonlítására is megad a fizika egy fogalmat, az energiát. Szokásos azt mondani, hogy az energia megmarad, valójában a fizika úgy alakítja ki ezt a fogalmat, hogy keresi a változó mozgásban is az állandóságot. Ezt úgy adja meg, hogy bevezet egy sebességtől függő mennyiséget, a kinetikus, vagy mozgási energiát – ami a sebesség négyzetének és a tömeg szorzatának a fele – és ehhez adja hozzá a potenciális energiát, ami az erő képességét fejezi ki, hogy mekkora változást idézhet elő a fizikai objektum kinetikus energiájában. Ez utóbbit tekinti a fizika az erő munkavégző képességének, ami alatt az erő irányában történő elmozdulást ért. Az erő a potenciális energia térbeli változásától függ, mégpedig avval egyenlő, hogy mekkorát változik a potenciális energia két egységnyi távolságú térpont között (ezt nevezi a matematika gradiensnek).
Fogalmi változások a relativitáselméletben
A klasszikus mechanika felsorolt fogalomrendszere jelentős változáson ment át a modern fizikában egyrészt a relativitáselmélet, másrészt a mikrovilág mechanikája, a kvantummechanika létrejöttével. A klasszikus felfogás szerint a tér abszolút és az idő abszolút, azaz a tárgyhoz egyértelmű hosszúság, az inga lengéséhez egyértelmű időtartam tartozik. Ezt írja felül a speciális relativitáselmélet, amikor a mérés eredményét attól teszi függővé, hogy abban a rendszerben határozzuk-e meg a fizikai adatokat, ahol a vizsgált tárgy van, vagy egy hozzá képest mozgó rendszert veszünk-e alapul. A tér ezáltal részben idővé, az idő pedig térré válik, ezt fejezi ki a Minkowski által bevezetett új fogalom a téridő. Ebben a téridőben nem beszélünk a különálló háromdimenziós térről és az egydimenziós időről, itt már a fizikai fogalmakat négydimenziós vektorokkal írjuk le. Hasonló fogalomváltozás következik be a tömeg esetében is, ami többé nem a tárgy abszolút tulajdonsága, mert ha a tárgyhoz képest mozgó rendszerből vizsgáljuk, akkor nagyobb lesz a tömeg és így meg kell különböztetni a nyugalmi és a mozgási tömeget. Ez a nyugalmi tömeg is új jelentéstartalmat kap a tömeg és az energia E = m.c2 ekvivalenciájában. A tömeg ebben az értelemben koncentrált energia, ami a tömegvesztési folyamatokban mozgási energiává alakítható. A mozgási energia viszont az impulzusban manifesztálódik, ezért beszélünk a négydimenziós téridőben a szintén négydimenziós energia-impulzus vektorról. A fizika az állandóságot keresi a változásban, ezt adja meg a téridőben is a kovariánsok fogalmával. Ilyen kovariánst alkot a tér és idő koordináták, illetve az energia és az impulzuskomponensek négyzeteiből.
A tömeg és tér összekapcsolása az általános relativitáselméletben
A tömeg fogalma újabb jelentésváltozáson megy át Einstein általános relativitáselméletében. Ebben már a tér és a tömeg fogalmai kapcsolódnak össze. Nincs is többé egyenes koordinátákkal meghatározott euklideszi tér, belép a görbült tér fogalma. Ahol nincs tömeg, ott egyenesek a koordináták, de ott mi értelme van térről beszélni ahol, nincs is anyag? Ez üres absztrakció! Ahol viszont van, ott görbül a tér annak mértékében, hogy mekkora a benne lévő, illetve mozgó tömeg. A gravitáció nem más, mint a görbült koordinátákhoz való „igazodás” a mozgás során. A mozgó tömeg kialakítja azt a teret, amiben mozog, tehát a tömeg saját mozgására hat! Így kerül elválaszthatatlan kapcsolatba a téridő és a tömeg. Ezekről a fogalmakról ezért nem is lehet külön-külön beszélni.
A téridő-részecske fogalma
A fogalomalkotás újabb lépéseként vezettem be a téridő-részecske fogalmát. Az einsteini koncepció a nagy tömegek által görbített térről szól, ezt terjesztem ki az elemi részecskék világára. Elképzelésem szerint minden részecske a téridő fénysebességű önmozgásának megnyilvánulása, amely a tér extrém mértékű görbületét hozza létre (lásd:”Térgörbület és gravitáció forgó rendszerekben”, „A tér szerkezete és az elemi részecskék mint rezonanciák”, „Az egységes fizikai világkép”). Ez forrása a tömegnek, forrása a spinnek és az elektromos töltésnek is, amit a speciális és az általános relativitáselmélet alapelveinek összekapcsolásával lehet kimutatni.
Új fogalmak a kvantummechanikában
A mikrovilág leírására van egy kitűnő matematikai módszerünk, a kvantummechanika, de mintha a fogalomépítésben lemaradás lenne. Evvel magyarázom, hogy miért van annyi ellentmondó értelmezése az elméletnek. Mintha nem igazán sikerült volna beépíteni gondolkozásunkba, hogy a kvantummechanikai valószínűség valójában mit is jelent és miért lép fel a mikroszkopikus folyamatban.
Az alapkérdés a folytonosság és a diszkontinuitás viszonya, az utóbbit testesíti meg a kvantum fogalma. Azt már Démokritosz is felvetette, hogy amikor bármilyen anyagot kisebb részekre bontunk, eljutunk egy határhoz, ami már nem aprózható fel, illetve aminek további bontása már más minőséghez vezet. Erre példa a fizikában, amikor egy anyagot molekuláira bontunk. Ha tovább bontjuk a molekulát, akkor átlépünk egy határt, mert ekkor új minőséghez jutunk, az atomhoz. De az atom is összetett struktúra, felbontható az elektronokra és az atommagra. Az atommag is tovább bontható protonokra és neutronokra, vagy összefoglaló néven a nukleonokra. A modern fizika azt is kimutatta, hogy a nukleonok is összetettek, amit a kvarknak nevezett elemi részecskék építenek fel. Ez az utolsó lépés azonban már lényegesen különbözik az előbbiektől, mert ez a felbontás kísérletileg nem valósítható meg. Ez csupán elméleti konstrukció, ami lehetővé teszi néhányszáz elemi részecske szerkezetének rendszerezését kisszámú kvark segítségével (lásd: „Barangolás a kvarkok és elemi részecskék világában”). Az elemi részecskék elméletének egyik nagy dilemmája, hogy a nukleonok miért nem bonthatók fel az elemi kvarkokra, vagy más szóval a „szabad” kvark miért nem létezik? A magam részéről ezt avval magyarázom, hogy csak olyan részecske mutatható ki önmagában, amely rendelkezik valódi tömeggel és valódi töltéssel (lásd „A tömeg és a töltés kettős arculata”, illetve „A Dirac-egyenlettől az általános fermion egyenletig”. Itt csak előrevetítem a kvantummechanikai valószínűség és a hullámfüggvény redukciójának kérdését: a mérés elvégzése előtt a fizikai paraméterekre – beleértve a tömeget és a töltést is – csak valószínűségi kijelentést tehetünk, de maga a mérés már egy „megvalósult” határozott értéket jelöl ki. Ebben a tekintetben a kvark is egy kvantummechanikai valószínűségi állapot, míg a mérés egy „megvalósult” fizikai állapotot hoz létre, ami a „megfigyelhető” nukleonokban és más elemi részecskékben mutatkozik meg).
Termodinamikai fogalmak
Mielőtt a kvantum fogalmához eljutnánk, szükség van a termodinamika néhány fogalmának megértésére is. A termodinamika olyan rendszereket vizsgál, ahol olyan óriási az egyes elemek száma, ami lehetetlenné teszi az egyedi objektumok viselkedésének leírását, viszont bevezethetők olyan fogalmak, ami az egész rendszerre vonatkozik és leírják az egész rendszer állapotát és annak változását. Ilyen fogalmak a hő, a belső energia, a hőmérséklet és az entrópia. Ez utóbbiról ejtettem szót az „Energia, entrópia és evolúció” című bejegyzésben. A hő a teljes rendszer rendezetlen mozgásának összes energiáját, a hőmérséklet pedig annak átlagát jellemzi, az entrópia kifejezi, hogyan tart a rendszer a többféleképpen és a nagyobb valószínűséggel megvalósuló állapotok felé. Itt túl messzire vezetne végigvenni a fogalmak definícióját, csak arra térek ki, ami elengedhetetlen a kvantum fogalom kialakulásának előzményeihez.
A kvantum elv születése a hősugárzás elméletében
A kvantum fogalmának kialakulása a fekete test sugárzási törvényének magyarázatához kötődik. Fekete test alatt a termodinamika olyan testet ért, amely a legtöbb sugárzást képes elnyelni és kibocsátani egy adott hőmérsékleten. A kibocsátott energia frekvencia eloszlását Rayleigh és Jeans határozták meg a klasszikus fizika törvényei alapján:
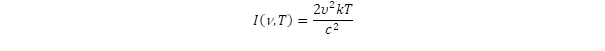
Itt ν a kibocsátott sugárzás frekvenciája, T az abszolút hőmérséklet, k az általános gázállandó és c a fénysebesség. Ebből a törvényből az követezik, hogy a kibocsátott sugárzás intenzitása a frekvencia négyzetével arányosan növekszik. Ez igaz is egy kritikus frekvencia alatt, de efelett már nem növekszik tovább, hanem fokozatosan csökken és nagy frekvenciákon már az intenzitás elhanyagolható mértékű lesz. A klasszikus fizika termodinamikája tehát nyilvánvalóan ütközik a fizikai valósággal, mert olyan következtetésre jut, hogy elvben végtelen intenzitású sugárzást képes kibocsátani a fekete test nagy frekvenciákon, ezt nevezi a szakirodalom ultraviola katasztrófának.
Mi okozza a klasszikus fizika csődjét? Ezt a kérdést vetette fel Planck is. Először is azt kell értenünk, hogy mit jelent a fenti formulában „kT”, azaz a gázállandó és a hőmérséklet szorzata. Evvel jellemzi a termodinamika a vizsgált rendszer egyes elemeinek (molekulák, atomok) mozgásformáinak (rezgések, transzlációk, forgások) átlagos kinetikai energiáját. Ez a kinetikai energia a kibocsátott sugárzás forrása. Az energia megmarad, ezért a kisugárzás energiaveszteséget okoz. De mekkora energiát bocsáthat ki egy-egy molekula, amelynek kinetikai energiája átlagban kT-vel arányos? Ez nem lehet nagyobb a molekula mozgási energiájánál. Hogy kapcsolódik ez a sugárzás frekvenciájához? Ha egy adott frekvenciájú sugárzás intenzitása bármennyire lecsökkenthető, akkor nincs akadálya, hogy tetszőlegesen nagy frekvenciájú sugárzást bocsásson ki a mozgást végző molekula, mert ezt a klasszikus fizika folytonossági elve lehetővé teszi! Itt van tehát a hiba, állapította meg Planck, és kimondta, hogy kell lenni egy határnak, amely megmondja mekkora a ν frekvenciájú sugárzás legkisebb és tovább már nem osztható egysége, amelynek energiája E = h.ν. Ezzel a fény, az elektromágneses sugárzás fogalmát mélyítette tovább, bevezetve annak kvantumát, a fotont. A termodinamika Boltzmann-eloszlási törvénye megmondja, hogy ha a részecskék mozgási energiájának átlaga kT, akkor mekkora a száma az ennél nagyobb, illetve kisebb energiájú részecskéknek. Ez az energia és kT arányával adható meg egy exponenciális függvény segítségével. Planck evvel bővítette ki a Rayleigh-Jeans formulát és írta le a teljes frekvencia tartományban a kísérleti adatokkal egyező eloszlási törvényt:
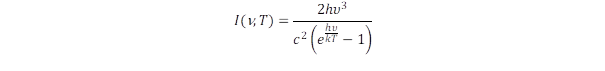
A fény kvantuma a foton
Plancknak ez a felfedezése megnyitotta az utat a mikrovilág titkainak feltárásához, mert evvel a fotonnak, az információ forrásának tulajdonságait határozta meg. Ennek hiánya nem okozott gondot a klasszikus fizikában, mert minden objektumról olyan nagyszámú foton érkezett, hogy fel sem merült, hogy a fény intenzitásának van egy alsó határértéke. Érdemes ezt még mindennapjaink tapasztalatával kiegészíteni. Ha felpillantunk a csillagos égre, akkor megfelelő távcsövek segítségével eljut hozzánk még a nagyon távoli galaxisok fénye is. Ha a fényintenzitás tetszőlegesen kicsiny lehetne, akkor túl kicsi lenne annak energiája, hogy szemünkben megindítsa azt a folyamatot, ami a látáshoz kell. Mivel az egyes fotonok energiája nem csökken le, csupán számuk lesz kisebb a távolsággal, így meg van rá az esély, hogy megpillantsuk a távoli csillagokat is.
Kvantummechanika operátorai a hatás-elv alapján
A fotonok kvantumos tulajdonságán alapul, hogy a mikrovilág is kvantumosnak mutatja magát (lásd: „Foton: a mikrovilág postása és szabályozója”). Ez a kvantummechanika egyik kiindulópontja, de van egy másik is, amelyik a fizikai fogalmak, mint az impulzus, az impulzusnyomaték és az energia fogalmának mélyítésén alapul. A klasszikus fizika ezeket a mennyiségeket egymáshoz, illetve a tömeghez, sebességhez és gyorsuláshoz való viszonyában határozta meg. A kvantummechanika operátor fogalma viszont abból indul ki, hogy az impulzus fenntartja az állandó sebességű mozgásokat, az impulzusnyomaték az állandó frekvenciájú forgást, az energia pedig a mozgási állapot időbeni fenntartásának felelőse. Ezt fejezi ki a Noether-elv, amikor a térbeni, illetve időbeli kezdőpont választásától teszi függetlenné ezeket a mennyiségeket. Ezért lépnek fel az impulzus és energia operátorban a tér- illetve idő szerint képzett differenciálhányadosok, melyek együtthatóját a h Planck állandót a foton impulzusa és energiája határozza meg (lásd: „Út a kvantummechanika megértéséhez”).
Állapotfüggvény: a kvantummechanika pályafogalma
A kvantummechanika kulcsfogalma az állapotfüggvény. Mivel a fizikai mennyiségeket hatásuk alapján operátorok írják le, így akkor jellemzi az egyes állapotot az impulzus, vagy az energia, ha az operátor egy speciális számérték esetén az állapotot leíró függvényt nem változtatja meg. Ezt nevezi a kvantummechanika sajátértéknek, melynek értéke kötött állapotban diszkrét értékeket vehet fel. A hatás operátorokat a klasszikus mechanika mozgásegyenleteibe helyettesítve jutunk el a kvantummechanika alapegyenletéhez, a nem-relativisztikus esetben a Schrödinger, a relativisztikusban a Dirac egyenlethez. Ezek sajátértékéhez tartozó függvények az állapotfüggvények. Kötött állapotban az időtől nem függő energiákhoz tartozó sajátfüggvények írják le a rendszer stacionárius állapotát. Ez az állapot új értelmet ad a pálya fogalmának, amely egyrészt nem függ az időtől, viszont valószínűségi eloszlást rendel a részecske pozíciójához és impulzusához. A valószínűség megjelenése okozza, hogy egyik mennyiség sincs pontosan meghatározva és a két mennyiség bizonytalanságának szorzata szintén a Planck állandó. Ezt nevezik Heisenberg nyomán a határozatlansági relációnak.
A mikrovilágban az idő dimenzióját felváltja a valószínűség fogalma
Nézzük meg, hogyan következnek a fenti fogalmak a foton tulajdonságaiból! Amikor egy labda pályáját követjük, akkor minden pillanatban és pozícióban fotonok serege érkezik szemünkbe, ezért a labda pályáját a tér és idő fogalmaival jól írhatjuk le, de mi a helyzet az elektronnal. Két esetet különböztessünk meg
- amikor az elektronpályát elektromágneses mezőben, például egy gyorsítóban követjük
- amikor egy atomban, vagy molekulában írjuk le a stacionárius pályán mozgó elektron pályáját.
A gyorsítóban mozgó elektron folytonosan elektromágneses sugárzást bocsát ki, emiatt pályája hasonlóan jellemezhető a tér és idő koordinátákkal, mint a labdáé. Emiatt a pálya leírása is megtehető a klasszikus mechanika szabályaival. Más a helyzet a molekulában, vagy az atomban, ekkor a stacionárius állapotban egyáltalán nem kerül sor foton kibocsátásra, azaz nem „láthatjuk” egyáltalán az elektront. Csak azt tudjuk megfigyelni, amikor az elektron ugrást végez két állapot között, mert ekkor fotont bocsát ki, vagy nyel el. Ezt a fotont megfigyelve jellemezhetjük az elektron állapotváltozását. Mi viszont a kvantummechanikai leírásban a stacionárius állapotról beszélünk, amiről nincs közvetlen információnk és ezért az idő fogalma alkalmatlan a pálya leírására. Amire következtethetünk az csak annak a valószínűsége, hogy az „ismert” kölcsönhatás alapján (az elektronok és atommagok közötti Coulomb erők) az elektron hol lehet. Ez már valószínűséget jelent. Úgy is fogalmazhatunk, hogy az időbeli mozgás helyett a valószínűségi mezőben írjuk le a mozgást. Mozgásról jogos beszélni, mert az állapothoz rendelhetünk energiát, impulzust és impulzusnyomatékot (spint) is. Az idő „elvesztésén” kívül a szokásos térkoordináták sem alkalmazhatók az elektronpálya jellemzésére. Milyen kölcsönhatás éri az elektront például a Hidrogén atomban? A kölcsönhatás ereje kizárólag attól függ, hogy mekkora a távolság az elektron és a proton között. Az irány tehát nem befolyásolja az elektron mozgását. A kvantummechanikai leírás azonban tartalmazza az irányt, de ténylegesen ennek a fogalomnak ekkor nincs értelme. Mit tesz ezért a kvantummechanika? Olyan állapotfüggvényt ad meg, ahol minden irányhoz azonos valószínűséget rendel. Ugyanígy értelmezhetjük az elektronok „p” pályáit is. Például a benzol molekulában, ahol a hat szénatom egy szabályos hatszöget alkot a síkban, a „p” pályáknak két része van: félig a sík „alatt” és félig a sík „fölött” van az elektron egyenlő valószínűséggel, de magában a síkban nulla valószínűséggel található meg. De ha egy elektronról van szó, ami nem vágható ketté, akkor hogyan „közlekedik” az elektron a két részpálya között? Sehogy! Valójában arról van szó, hogy nincs olyan kölcsönhatás, amelyik megkülönböztetné a sík két oldalát. Az „alatt” és „fölött” csupán a makrovilágban értelmezhető. Mivel ekkor ezek a fogalmak nem érvényesek, a kvantummechanika is csak egyet tehet: egyenlő valószínűséget rendel a valójában megkülönböztethetetlen tartományokhoz. Ezt a gondolatmenetet szemléltem az elektron és a fizikus közötti dialógus segítségével „Az intelligens elektron” című bejegyzésben.
A foton tulajdonságai jelennek meg a határozatlansági relációban
A határozatlansági reláció közvetlenül származtatható a foton tulajdonságaiból, mert a foton hullámhosszának és impulzusának szorzata épp a Planck állandó. A hullámhossz behatárolja a pozíciómérés pontosságát, ha a pontosságot fokozni akarjuk, akkor rövid hullámhosszú sugárzást kell választani, de ekkor az impulzus lesz nagyobb. A mérés az ókori görög filozófus (Hérakleitosz) ismert mondásával jellemezhető: „nem lehet kétszer egymás után ugyanabba a folyóba lépni”. A pozícióméréshez használt foton impulzusa megváltoztatja a mérendő objektum impulzusát, ezért ha egy következő mérést végzünk az impulzus meghatározására, az már a részecske megváltozott állapotára fog vonatkozni. Ezért a két mérés pontosságának szorzata nem szorítható a Planck állandó alá.
Logikai csapda: lehet-e a kiválasztani egy elektront
A kvantummechanika nem tudja megmondani, hogy a molekulában egy „kiszemelt” elektron épp mikor fog átugrani két állapot között, viszont meghatározza az esemény valószínűségét. Itt a logikai csapda ott van, hogy nem lehet egy elektront „kiszemelni”, mert az már mérést, azaz fotonnal való kölcsönhatást jelent. Amíg nincs kölcsönhatás, addig időt sem rendelhetünk a pályához, így nincs olyan viszonyítási alap, amivel az ugrás időpontját összevethetnénk. Egy lehetőség marad, hogy megmondjuk mekkora az elektronugrás valószínűsége, ezt pedig megmondja a kvantummechanika.
Kvantummechanikai paradoxonok
Kicsit más meggondolást kíván az olyan eset, amikor úgy bocsátunk ki fotonokat egy berendezésből, hogy külön-külön lépjenek kölcsönhatásba valamilyen detektorral. Mi határozza meg ekkor, hogy sok detektor közül melyik fog megszólalni? A választ a hullámfüggvény fázisa adja meg. Ahogy az interferencia során ott jön létre kölcsönhatás, ahol a hullámfázisok egyeznek, ez történik a detektor elektronjának és a foton fázisával is. De ezt a fázist nem ismerjük, erről nincs információnk. Az információ hiányában ismét csak valószínűséget adhat meg a kvantummechanika. Ilyen és hasonló esetek sorát (kétréses kísérlet, két-fotonos kísérlet, összefonódott kvantumállapotok, Schrödinger macskája) tárgyalja „Einstein igazsága és tévedései. Gravitációs hullámok és az EPR paradoxon_II” című bejegyzés.
A hullámfüggvény redukciója
A kvantummechanika sokat vitatott kérdése, hogyan értelmezzük a hullámfüggvény redukcióját? Itt arról van szó, hogy a mérés előtt a hullámfüggvény valószínűség eloszlást ad meg a fizikai paraméterekre. Viszont a mérés bekövetkezésekor a lehetőségek közül csak egy valósul meg. Mérjük meg például egy foton polarizációs síkját. A kibocsátáskor a hullámfüggvény minden irányt megenged, de a mérés csak egyetlen irányt határoz meg. Hogyan történt az átalakulás? Valójában nem a foton polarizációs síkja rögzül egy lehetséges irányban, hanem a kibocsátáskor még értelmetlen irányfogalom nyer értelmet a mérés során. Amikor elvégezzük a mérést, az irányt például egy mágneses pofa síkjához viszonyítjuk. Ezt a síkot ismerjük, mert onnan számtalan foton jut a szemünkbe, ezért van értelme az iránynak. A foton kibocsátáskor még nincs kapcsolat a mágnes síkja és a foton között, ez csak a méréskor realizálódik. Ekkor viszont nem csak azt az információt használjuk fel, ami a vizsgált fotonra vonatkozik, hanem a többit is, amit a mágneses pofáról kapunk. A hullámfüggvény redukciója tehát nem annak átalakulásáról szól, csak az információ kibővüléséről.
Miért nem figyelhető meg szabad kvark?
Már az előzőekben felvetettük a kérdést, hogy miért nem láthatunk szabad kvarkokat, csak a belőlük felépített nukleonokat. A kvarkokat úgy foghatjuk fel, mint egy kvantumállapotot, amelyben a tömeg és a töltés nem rendelkezik jól definiált értékkel, csupán bizonyos valószínűséget rendelhetünk a tömeg és a töltés lehetséges értékeihez. A modern fizika Standard Modellje is csak renormált, azaz nem valódi tömegről beszél a kvarkok esetében, míg a tört töltés úgy fogható fel, mint a töltésoperátor várható értéke. Bármely részecske megfigyeléskor viszont a tömegnek és töltésnek jól meghatározott értéke van, ez azt jelenti, hogy a lehetséges tömeg és töltés értékek közül valamelyik megvalósul. A kvark tehát úgy fogható fel, mint egy detektálás előtt még határozatlan részecskeállapot, aminek tömegéről és töltéséről csak valószínűségi kijelentéseket tehetünk. A detektálás már konkrét tömeg és töltést jelent, amivel csak a kvarkokból felépülő nukleonok és egyéb részecskék rendelkeznek.
Tovább bontható-e a kvantum?
Az anyag egyre apróbb részekre bontásának, mint láttuk, több lépcsőfoka van. Jelenlegi részecskefizikát összegző Standard Modell csak olyan elemi részecskékről beszél, amelyeknek van spinje, azaz saját impulzusnyomatéka. Ennek egysége a Planck állandó, ezért a spin a kvantumtulajdonságok letéteményese, evvel rendelkezik a foton is. A részecskék spinje vagy 1, vagy ½, amit avval magyarázok, hogy a spint fénysebességű egyszeres, vagy kétszeres forgások hozzák létre, és ekkor a relativitáselmélet szerint az impulzusnyomaték nem függ a forgási frekvenciától. Ezért lesz a Planck állandó ugyanolyan univerzális tulajdonsága a téridőnek, mint a fénysebesség. Amikor „forgást” rendelünk a spinhez, akkor felmerül, hogy lehet-e olyan részleges forgás a téridőben, amely nem jut el egy teljes fordulathoz? Ha igen, akkor ez egy kvantum előtti állapot lenne. Ebben az állapotban már nem alakulnának ki az elemi részecskék fizikai paraméterei. Ilyen állapotról lehet beszélni az ősrobbanás után a Planck idő előtt (lásd: „A kvantumelv határai a mikrofizikában”). Ez lenne az ősállapot, a káosz birodalma, ahol már újra kellene értelmezni a fizika fogalmait.
„A fizika kalandja.blog.hu” további írásainak összefoglalóját lásd „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”
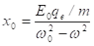
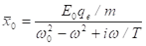
Nqe/2ε0 kifejezéssel kell helyettesíteni, ahol N adja meg a térfogategységre jutó qe töltések számát, ε0 pedig a töltésegység megválasztásától függő arányossági tényező (a vákuum dielektromos állandója):