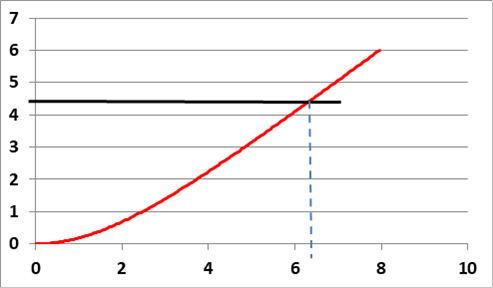
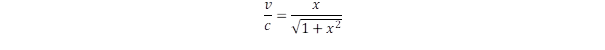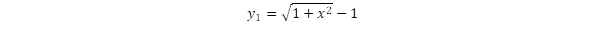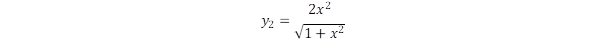A két kommentben is felvetett kérdés kapcsolódik ahhoz a logikai csapdához, amiről „A valódi és az elképzelt fizikai világ konfliktusa” című bejegyzésben is írtam. Mivel ez a probléma végighúzódik a kvantummechanika értelmezésének egész történetén, bővített formában ismét kifejtem álláspontomat.

A rejtett paraméter

Einstein annak idején két szerzőtársával (Podolsky és Rosen) a kérdést úgy vetette fel, hogy a kvantummechanikát kiegészítve valamilyen rejtett paraméterrel eljuthatunk egy olyan fizikai képhez, amelyben a mikro-folyamatok is determinisztikusak lesznek. Erre adta Bell azt a választ, hogy ez nem lehetséges. Azóta a fizikusok többsége Bell álláspontját fogadta el. De tényleg igaza volt-e Bellnek, vagy csupán egy logikai csapdával van dolgunk?

A Stern-Gerlach kísérlet

Ennek megértéséhez induljunk ki a kvantummechanikát megalapozó egyik legfontosabb kísérletből, amit Stern és Gerlach hajtottak végre 1922-ben. Kísérletükben ezüst atomok mozgását vizsgálták inhomogén mágneses mezőben, de hasonló kísérlet végezhető bármilyen töltött részecskével, így fókuszált elektronnyalábbal is. Az inhomogén mező azt jelenti, hogy felülről lefelé haladva a mező erőssége fokozatosan változik és a változás mértéke határozza meg, hogy mekkora erőt gyakorol bármilyen mágneses (azaz mágneses nyomatékkal rendelkező) részecskére. A mágneses nyomaték vektor jellegű mennyiség, azaz nagyságán kívül annak iránya is fontos, amit nyilakkal jelölhetünk. Az elektronnyalábot úgy képzelhetjük el, hogy ebben a nyilak tetszőleges irányban lehetnek és az erőhatás mértéke attól függ, hogyan viszonyul a nyíl iránya az inhomogén mágneses mező irányához. Ha avval párhuzamos, akkor a kiválasztott elektron pályája felfelé, ha ellentétes, akkor lefelé tér el, de ha a mágneses mezőre merőleges, akkor nem tér ki az eredeti irányhoz képest. A klasszikus fizika alapján ezért azt várnánk, hogy a részecskék egy vonal mentén ütköznének a detektor felületére.

A mérés kvantált eredménye

A megfigyelés azonban más eredményt hozott! Ha elektronról, vagy más mágneses nyomatékkal rendelkező elemi részecskéről van szó, akkor a detektornak csak két pontjába érkeztek meg a részecskék. Ezt úgy foghatjuk fel, hogy a részecskék egy olyan mágneses „kapun” haladnak át, amelyik függőleges irányba forgatja el a „nyilakat”, amelyek aztán vagy lefelé, vagy felfelé mutathatnak. Ezt nevezzük polarizációnak. Klasszikusan gondolkozva ezt úgy foghatjuk fel, ha a nyíl inkább felfelé mutat, akkor ebben az irányban megy át a kapun, ha fordított a helyzet, akkor lefelé.

Kvantummechanikai értelmezés

De mit mond erre a kvantummechanika? Az elmélet szerint csak két lehetséges állapot van, amelyik meghatározza az elektron nyomatékának (impulzus és mágneses) irányát, amit a spin két lehetséges értékéhez rendel (+½ és – ½), az egyik a „fel”, a másik a „le” és csak arról beszélhetünk, hogy a két állapot mekkora valószínűséggel valósul meg. Ha nincs előzetes polarizáció, akkor mindkét állapot valószínűsége azonos lesz. Ez a statisztikai interpretáció nem is okoz gondot mindaddig, amíg nagyszámú elektronról van szó, de mi történik, ha egyesével indítjuk az elektronokat, mi határozza meg, hogy felfelé, vagy lefelé mozdulnak el az eredeti irányhoz képest?

Einstein determinisztikus elképzelése

Erre a kérdésre kereste a választ Einstein is, amikor felvetette azt a lehetőséget, hogy létezik egy rejtett paraméter, amiről nem ad számot a kvantummechanika és ez határozza meg, hogy milyen irányban mozdulnak el a mágneses részecskék. Más szóval a mi esetünkben ezt úgy értelmezhetjük, hogy tényleg létezik egy polarizációs irány nem csak párhuzamosan, vagy ellentétesen a mágneses mezővel és ez a mérés során „beforogna” a mágneses mező által kijelölt irányba.

Bell cáfolata

Itt jön be a képbe Bell elgondolása, aki egy szellemes elvi kísérletet javasolt, amikor két különböző Stern-Gerlach mérést képzelt el, ahol a két mérésben a mágneses mező merőleges egymásra. Abból indult ki, hogy a két mérésben nem csak a mérés pillanatában rögzíti a rejtett paraméter a polarizációs irányt, hanem a részecske keletkezési pillanatában is. Ez egy plauzibilis feltevésnek tűnik, de mint látni fogjuk, épp ez a levezetés gyenge pontja.

 A kvantummechanika valószínűségi elvére alapozva kimutatta Bell, hogy a két mérés együttes valószínűsége korlátozott (ez a nevezetes Bell-egyenlőtlenség) és nem érheti el azt a bizonyosságot, amit a rejtett paraméter létezése megkíván. Logikus következtetés: a kvantummechanika nem egészíthető ki rejtett paraméterrel.

Aspect mérése cáfolja a kvantummechanikát?

Először Aspect végzett el olyan kísérletet, amelyik cáfolni látszik Bell következtetését, azaz a kvantummechanikát. Ő két fotont indított el egyetlen aktusban és figyelte meg a fotonokat azonos távolságban a forrástól, de ellenkező irányban. A foton is rendelkezik spinnel, amiért polarizálható. Ekkor a mérési technika nem a Stern-Gerlach kísérlet, de elvi szempontból ennek nincs jelentősége, a lényeg, hogy ekkor is a polarizációs irány kerül meghatározásra. A mérés eredménye szerint a két foton polarizációja egyértelmű korrelációt mutatott, ha az egyik polarizáció „fel” volt, akkor az esetek többségében a másiké „le” irányba mutatott. Tehát van valami, ami összeköti a két foton polarizációját még pedig egy és ugyanazon pillanatban!

Nem-lokális rendszer koncepciója

A kvantummechanika, amelyik olyan jó leírást ad a mikrovilág jelenségére, ebben az esetben csődöt mondana? Ezt próbálja feloldani a nem-lokális állapot koncepciója, amelyik a két fotont szétválásuk után is egyetlen rendszernek tekinti, és így az egyik foton polarizálása automatikusan magával rántja a másikat is. Erről a jelenségről szól részletesen korábbi bejegyzésem („Hogyan hozhatunk létre teleportálást a kvantummechanika szerint”), de most nem arra akarok hivatkozni, hogy hányszor írtam már le érveimet, hanem inkább megismétlem, mert a dolog lényeges és egyáltalán nem magától értetődő!

Ütközés a relativitáselmélettel

A nem-lokális kölcsönhatás ugyan segít megmenteni a kvantummechanikát, de létrehoz egy másik ellentmondást, mert olyan kölcsönhatáshoz vezet, ami a tér két különböző pontja között létrehoz egy fénynél gyorsabb (sőt végtelen sebességű) kölcsönhatást. Ez persze még nem cáfolat, csak rámutat a konfliktusra a különböző elméletek között. A cáfolatot én nem itt keresem!

Mikor használhatjuk az irány fogalmát?

A hiba a fogalmi rendszerünkben van. Az irány fogalmát csak akkor használhatjuk, ha ténylegesen összehasonlítjuk legalább két foton pályáját, ami a szemünkbe, vagy a műszerünkbe jut. Erre sor kerül a polarizációs mérés során, mert a polarizációt a mágneses mező által definiált irányhoz viszonyítjuk. Itt a „függőleges” irányt a mágnes jelöli ki, Bell szintén erre vonatkoztatja a kibocsátásnál az induló polarizációs irányt, amit elgondolása szerint a rejtett paraméternek kellene kontrollálni. Hétköznapi gondolkozásunkban teljesen természetes, ha ismerjük a függőleges irányt szobánk egyik sarkában, akkor ezt használhatjuk a másik sarokban is. Ennek oka, hogy látjuk a falakat, látjuk a padlót és a mennyezetet, hiszen mindenhonnan rengeteg foton árad felénk. Emiatt egységes tér és irányfogalommal rendelkezünk. De jogos-e a mágnes által kijelölt irányt használni a kísérletben használt foton forrásnál is? Jogos lehet, ha a mágneses mező ott is jelen van, de ez elvileg sem valósítható meg. Ugyanis, ha ott is van mágneses mező, az beleszól a kísérletbe, akkor már eleve polarizált részecskéket bocsátunk ki, és emiatt Bell kiinduló feltétele már nem lesz érvényes! Meghatározhatunk valamilyen irányt a foton kibocsátáskor más technikával? A probléma, hogy bármilyen módszert választunk, az megváltoztatja a részecskék állapotát.

Az irány határozatlansága miatt lép fel a valószínűség!

Tehát kölcsönhatásmentes viszonyok között kell a részecskéket elindítani, de emiatt a rejtett paraméter nem vonatkoztatható a külső irányokhoz, más szóval az irány fogalma értelmét veszti. Mit tehetünk ilyenkor? Azt mondhatjuk, hogy minden polarizációs irány egyformán valószínű. Pont ezt teszi a kvantummechanika is, amikor csak valószínűségeket ad meg. A kvantummechanika azért kitűnő eszköze a mikrovilág leírásának, mert választ ad minden megválaszolható (mérhető) kérdésre, de nem válaszolja meg a megválaszolhatatlan kérdéseket!

Tehát hiába létezik egy olyan paraméter, amely meghatározza a részecske „sorsát”, ezt a paramétert nem tudjuk a külső koordinátákhoz viszonyítani, más szóval határozatlan marad.

Az Aspect-kísérlet értelmezése

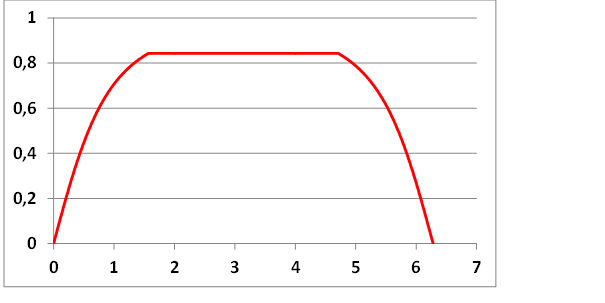
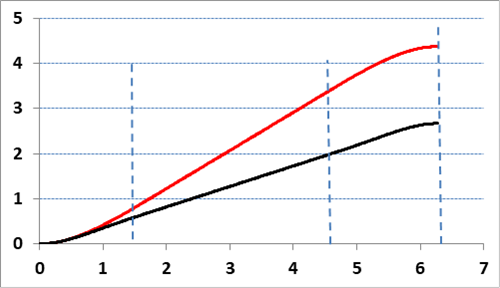
De mit mondhatunk az Aspect-kísérletekről, miért van korrelációban a két foton polarizációja? Ennek oka a fotonok belső meghatározó tulajdonságában rejlik. Amikor két foton jön létre egyetlen folyamatban, akkor a megmaradási elv miatt a kezdő polarizációs fázisok épp ellentétetek. A két foton frekvenciája megegyezik, ez az a frekvencia, ami a két foton polarizációját egyenlő ütemben forgatja el. Ha azonos idő után mérjük a két fotont, akkor az ellentétes polarizációs irány is megmarad. Tehát ugyan nem tudhatjuk, hogy a képződéskor milyen volt az eredeti polarizációs irány, de a kettő viszonya mégis meghatározott. Visszatérve Bell gondolatmenetére, ezért a rejtett paraméter nem jelenti azt, hogy meghatározott lenne az induló polarizáció és emiatt Bell-egyenlőtlensége érvényét veszíti.

Rejtett paraméter a forgási fázis?

A forgási fázis igazából nem is rejtett paraméter, hiszen ott van a kvantummechanikában, ez a stacionárius hullámfüggvény fázisa. Ez a fázis látszólag fölösleges, mert a sajátérték képzés során (abszolút érték négyzet) eltűnik. De mégis fontos szerepe van, mert ez határozza meg a fotonok, elektronok és atomok interferenciáját, de nem csak azt, hanem azt is megmondja, mikor kanyarodik az elektron a Stern-Gerlach kísérletben az egyik, vagy a másik irányba.

A fogalmi csapda

Miért marad meg mégis a fizikában az a kvantummechanikai kép, ami látszólag tagadja a mikro-folyamatok determinizmusát? Ennek oka, hogy rendkívül nehéz megszabadulni a hétköznapi világból nyert fogalmainktól és tudomásul venni, hogy másképp kell gondolkozni, amikor átlépünk a megfigyelhetőből egy a jelenséget magyarázó, de még is csak elképzelt világba. Az elképzelt világ törvényei nem azonosak a valódival, ahol észleljük és mérjük a jelenségeket. Ennek figyelmen kívül hagyása az a csapda, amitől a fizika nehezen szabadul meg. Ez határozza meg napjainkban is a kvantummechanika koppenhágai iskolájának felfogását.

A blog egyéb írásait összegzi és megadja a linkeket a „Paradigmaváltás a fizikában” című bejegyzés

Ha valamit nem ismerünk eléggé, akkor segít a képzelet, hogy kitöltsük a hézagokat. De a képzeletbeli fizikai állapotokat olykor összetévesztjük a valóságossal, és ilyenkor felléphetnek ellentmondások is. Erre mutatok be néhány példát a következőkben.

Mikor valódi a pálya?

Akár a kozmikus sugárzás, akár a gyorsítók által nagy energiára szert tett részecskék útját nyomon követhetjük, Erre azért van lehetőségünk, mert a részecskék nyomot hagynak a vizsgálathoz használt eszközeinkben, például az emulzióban, a köd- vagy a buborék kamrában. Az ionizáló sugárzás kémiai reakciókon keresztül válik láthatóvá és rajzolódik ki a pálya. Itt a lényeg a kölcsönhatás, ami a mozgás során helyről-helyre, pillanatról-pillanatra fellép és emiatt a megfigyelt pályát VALÓDI pályának tekinthetjük. Ezek a kölcsönhatások természetesen befolyásolják a pályát, de ettől eltekinthetünk, ha az egyedi kölcsönhatásokhoz tartozó energia sokkal kisebb, mint a részecske kezdeti energiája. Vizsgálhatjuk a pálya görbületét mágneses mezőben, figyelembe vehetjük az elektromos mező hatását is, és ez kulcsot ad számunkra, hogy meghatározzuk a részecske különböző tulajdonságait, így a töltését, tömegét és impulzusnyomatékát (spin) is.

Szintén valódi pályáról beszélhetünk makroszkopikus testek mozgásánál. Kövessük például a teniszlabda mozgását, ahogy ezt a „sasszem” is teszi, amikor vizsgálja, hogy a labda érintette-e a vonalat. A Napból érkező sugarak visszaverődnek a labdáról és eljutnak a videokamerába, amelyik a felvételt készíti. A fénysugarak gyakorlatilag folytonosan érkeznek, és hatásuk nem befolyásolja érdemben a labda pályáját, így jogosan tekintjük a video képet helyesnek a labda mozgásáról.

Mikor képzeletbeli a pálya?

De most ugorjunk egyet és tegyük fel a kérdést, mit tudunk mondani az egyes fotonok pályájáról, amíg a labdától a kamera felvevőjéhez, vagy a szemünkbe jut? Ezt úgy tudhatnánk meg, ha valahol menetközben végeznénk méréseket a foton kibocsátási helye és a detektor között. Ez természetesen kölcsönhatást igényel, amit már a kvantumelv szabályai igazgatnak, ami azt jelenti, hogy a fény impulzusnyomatéka, energiája, impulzusa is nagymértékben megváltozik. A detektálás után már nem ugyanaz a foton folytatja pályáját, azaz a pálya alapvetően más lesz, és így nem beszélhetünk a pályáról abban az értelemben, ahogy azt a részecske emulzióban rögzített nyoma, vagy a labda videokamerával felvett pályaíve esetén megtehetjük. Igazából csak két dolgot állapíthatunk meg a fotonról, az egyik a képződés helye és ideje, a másik az érkezésé. A kettő közötti utat csak képzeletünk tölti ki. Ez a KÉPZELETBELI pálya lehet egy egyenes, ami a kezdő és végpontot összeköti, de rajzolhatunk gömbhullámokat, amelyek szuperpozíciója értelmezi a foton útját Huygens elve szerint, de lehet a kvantumelektrodinamika módszere, amelyben oszcillátorok írják le az egyes fotonokat, de szemléltethetővé tehetjük a fotont a Feynman által bevezetett forgó nyilakkal is. Akármelyik ábrázolást is választjuk, mindegyik csak elképzelésünk egy-egy változata lesz. A fotont tulajdonképpen a tér két különböző helyén lévő elektron állapotának megváltozása definiálja, amikor a d távolságban lévő elektronokat összeköti valamilyen kölcsönhatás. Amit tudhatunk a kölcsönhatásról, hogy t = d/c idő telik el a két elektron állapotváltozása között (c a fénysebesség) és az egyik elektron energiája épp annyival csökkent le, mint amennyivel a másiké nőtt és ugyanezt elmondhatjuk egyéb fizikai jellemzők, így a mágneses kvantumszám változásáról is. Eddig ugyan elektronokról beszéltünk, de bármely más elektromosan töltött részecske állapotváltozása is vezethet fotonok kibocsátásához és elnyeléséhez.

A mezőelmélet foton képe

A kvantumelektrodinamika azonban túllép azon a képen, amely a fotonokat az elektronállapotok változásán keresztül definiálja, amikor mind a fotonokhoz, mind az elektronokhoz oszcillátorokat rendel. A részecskék megkülönböztető jegye a spin, az előbbinél a spin S = 1 (bozon), az utóbbinál S = ½ (fermion). A kétfajta részecske az elméletben egymást kölcsönösen definiálja. A kvantumelektrodinamika ezenkívül nem csak a változás dinamikáját, hanem a kölcsönhatás statikáját is leírja. Ezt úgy végzi el, hogy ez elektromos mezőt VIRTUÁLIS fotonok hatásához rendeli. Ennek legszebb alkalmazása, amikor az elektron anomális mágneses nyomatéka rendkívüli pontossággal kerül meghatározásra. Nincs a fizikában még egy olyan mennyiség, amit ekkora pontossággal ismernénk, és aminek elméleti reprodukálása ennyire pontos lenne. Virtuális fotonokon az elmélet azt érti, hogy ezek a fotonok egyidejűleg képződnek és eltűnnek, és létrehozzák az elektromágneses mező ingadozását a klasszikus fizika által meghatározott érték körül, viszont ezek a fotonok kísérletileg nem detektálhatók. Tehát az elmélet „bevallottan” képzeletbeli fotonok koncepciójára épül.

A valódi és a képzeletbeli pályák fogalmi ütközése

Az elektron anomális mágneses momentumának számolásánál a virtuális fotonok különböző folyamatait veszik alapul, melyeket a Feynman diagramokkal lehet sorba venni. Ilyen például elektron-pozitron párkeltési reakció. Még olyan folyamat is van, amikor egy elektron-pozitron pár előbb fejti ki a hatását, mint amikor létrejön. Szintén vannak olyan folyamatok, ahol a fotonok lokális terjedési sebessége meghaladja a fénysebességet. Zavarba ejtő kép, amely ellentmondani látszik a hétköznapi világból nyert fogalmainknak a térről, időről, az oksági elvről és ráadásul még a relativitáselméletnek is ellentmond. Valójában itt egy gondolati csapdával állunk szembe, aminek oka, hogy nem teszünk különbséget a valóságos folyamatok, a valóságos pályák és az elképzeléseink által alkotott folyamatok és pályák között. Pedig ez a különbségtétel az ellentmondások magyarázatának kulcsa, hiszen a virtuális világban könnyen képzelünk el olyan történéseket, amely ellentmondhat akár az oksági elvnek megengedve a múltba való visszatérést is. Ne gondoljuk azonban, hogy ez a képzeletbeli világ önkényes, vagy szubjektív lenne! Ebben a világban is szigorú törvények uralkodnak: a matematika egzakt szabályai.

Mit értsünk a hullámfüggvény redukciója alatt?

 A valóságos és a képzeletbeli dolgok megkülönböztetésének hiánya vezet el minket a kvantummechanika értelmezési dilemmáihoz is, amire nézzünk meg néhány példát! Az elképzelt jelleg jelenik meg az állapotfüggvény szerkezetében, amelynek abszolút érték négyzete írja le a molekulákban az elektron térbeli valószínűség eloszlását. Ugyancsak az állapotfüggvény határozza meg az egyes fizikai mennyiségek várhatóértékét. Az állapotfüggvény is képzeletünk matematikai terméke, amelynek jogosultságát az adja meg, hogy megadja a mérések lehetséges eredményét és ehhez valószínűséget rendel. Ha azonban elvégzünk egy mérést, az már egy határozott értéket ad meg a lehetséges értékek közül. Ez a megvalósult érték kijelöl egy állapotfüggvényt, amely már nem rendelkezik valószínűségi jelleggel, legalább is az éppen megmért fizikai mennyiség vonatkozásában. Az állapotfüggvénynek ezt a változását nevezi a koppenhágai iskola – amit ma a fizikusok többsége elfogad – a hullámfüggvény redukciójának. Ezt a redukciót azonban nem szabad valódi fizikai folyamatnak felfogni, bár sokan annak tartják, mert csupán arról van szó, hogy a lehetséges és képzeletbeli értékek közül egy kiválasztásra került a mérés során. A koppenhágai iskolának ezt a felfogását ezért a gondolati csapda egyik esetének tartom.

Mi határozza meg az egyedi fotonok sorsát?

Nézzünk meg most egy konkrét esetet. Amikor az üveglapra fényt bocsátunk, a fény 96 százaléka az üveglapon árhalad és 4 százaléka visszaverődik. De hogyan értelmezzük a jelenséget, ha a fényt egyedi fotonok sokaságából építjük fel? Képzeljünk el most egy fotont, amelyik megérkezik az üveglap felületére! Mi lesz a sorsa? Visszaverődik, vagy tovább halad? Kell lenni valamilyen egyedi szabálynak, hogy sok foton esetén a statisztika teljesüljön. Az egyik magyarázat szerint, amit statisztikai koncepciónak neveznek, valójában maga a kérdés rossz, hiszen mindig nagyszámú foton hoz létre detektálható eredményt. A magyarázat gyönge pontja, hogy van lehetőség az egyedi foton sorsának követésére. Legyen két detektorunk, két fotoelektron sokszorozó, ami elég érzékeny ahhoz, hogy képes legyen az egyedi fotonokat észlelni. Az egyik detektor a visszavert, a másik az áthaladó fotont detektálja. A fényforrásunk pedig olyan legyen, hogy csak ritkán bocsát ki egy-egy fotont, amelyek külön-külön adnak jelet. Eben az esetben már nem „gondolatkísérletről” van szó, hanem valódiról és jogunk van arra, hogy rákérdezzünk az egyes fotonok sorsára is!

Einstein gondolatkísérleteinek értelmezése

Vizsgáljuk meg Einstein két gondolatkísérletét! Egy fényforrást detektorokkal veszünk körül és a forrás egyenként bocsát ki fotonokat. Mindig csak az egyik detektor fog megszólalni, de honnan tudja a többi, hogy nekik hallgatni kell? Hasonló a dilemma a kétréses kísérletben, amikor egy zárt gömb van a fényforrás körül két szűk réssel, amin a fény áthaladhat. Ha kívül van egy fényérzékeny lemez, azon interferencia maximumok és minimumok jönnek létre. Sok foton esetén ez a fény hullámtermészetével magyarázható. Ha viszont egyesével indulnak el a fotonok, akkor nagyobb valószínűséggel érkezik meg a foton oda, ahol az interferenciának maximuma van. Az első példát úgy értelmezhetjük, ha a fotont részecskének képzeljük el, amelyik elindul valamilyen irányban és ez az irány jelöli ki, hogy melyik detektor fog megszólalni. A második példában már nem használható a részecske kép, mert az interferencia arra mutat, hogy a foton egyidejűleg áthaladt mind a két résen, ezt pedig csak egy hullám teheti meg, amelyet Huygens elve szerint minden pontban – így a két résen is – létrejövő újabb gömbhullámok szuperpozíciója hoz létre.. Most akkor hullám, vagy részecske a foton, tesszük fel a kérdést, vagy elképzelhető, hogy egyidejűleg mind a kettő? Ez ismét egy gondolkozási csapda, ugyanis arról van szó, hogy a foton pályája csupán képzeletbeli és nem valódi, az elképzelt pálya pedig többféleképp építhető fel. Dilemmánk abból fakad, hogy valóságosnak képzeljük a fantázia szülte képet, amikor a foton pályáját felépítjük. Az tekinthető valódi eseménynek, amikor az első elektron állapota megváltozik, ezt értelmezzük foton kibocsátásnak, utána változik meg egy másik elektron állapota valamelyik detektorban, erre mondjuk, hogy a foton megérkezett és elnyelődött. A két valódi esemény között keressük az oksági kapcsolatot, amit úgy oldunk meg, hogy kitöltjük a két esemény közötti időbeli és térbeli hézagot. Ez a „kitöltés” pedig a foton képzeletbeli pályája.

A fázis szerepe a fotonok reakcióiban

Hátra van még a KIVÁLASZTÁS kérdése: a kibocsátó elektron hogyan határozza meg, hogy melyik detektorban lévő elektron állapotát fogja megváltoztatni? A kvantummechanika erre csak valószínűségi választ ad. Einstein, aki determinisztikus képben gondolkozott a mikrovilág folyamataiban is, felvetette, hogy a kvantummechanika nem teljes, ki kell egészíteni valamilyen rejtett paraméterrel, ami eldönti az egyes események sorsát. Sok vitát kiváltó elképzelését két szerző társával (Podolsky és Rosen) együtt jelentette meg, ami a szakirodalomban az EPR paradoxon elnevezést viseli három szerző nevének kezdőbetűje alapján. Erről részletesen írtam a korábbi bejegyzésekben („Hogyan hozhatunk létre teleportálást a kvantummechanika szerint?”, „Einstein igazsága és tévedései: Gravitációs hullámok és az EPR paradoxon” bejegyzés második része). Itt most azt emelem ki, hogy épp a kiválasztás kérdése miatt nem csupán gondolati konstrukció a foton, hanem rendelkezik önmeghatározó tulajdonsággal is,ez pedig a foton fázisa, amely az energiájával arányos frekvenciával körbejár és meghatározza a pillanatnyi polarizációs irányt. A fázist a foton születésének pillanatában a kibocsátó elektron fázisa szabja meg. Az elektronnak is van fázisa, aminek bizonyítéka, hogy az elektronok között is megfigyelhető interferencia, és ez a fázis a hullámfüggvényben is szerepel, viszont ennek értékét nem tudhatjuk, mert erről nincs előzetes mérési információ. Determinisztikus elképzelésünknek az felel meg, hogyha pontosan ismerjük a kezdő feltételeket, akkor a folyamatok kimenetele is meghatározott lesz. Itt azonban ismét csak egy feltételezés, hogy pontosan ismerjük és képesek vagyunk reprodukálni a kezdő feltételeket, mert a fázist nem ismerjük és az ismeretlen fázis miatt csak valószínűségi kijelentéseket tehetünk a kísérlet kimenetelére. Einstein rejtett paraméterre vonatkozó koncepcióját az alapján cáfolják meg a szakirodalomban, hogyha ez a rejtett paraméter rögzítené a kezdeti polarizációs irányt, akkor olyan összefüggésekhez jutunk, ami ütközik a kvantummechanikai bizonytalansági elvével. De ez a cáfolat is gondolkozási csapda, mert arra a feltételezésre épül, hogy a polarizációs iránynak mérés nélkül is van valóságos értelme. Ez pedig nincs így, mert ha nincsenek fotonok, amelyek kijelölik az irányokat, akkor nincs jogunk irányról sem beszélni a kölcsönhatásban nem levő foton állapotának leírásában. Ugyanakkor Einsteinnek sincs teljesen igaza, mert a folyamatok sorsát eldöntő paraméter nem a kvantummechanikán kívül van, hanem annak szerves tartozéka. Amikor a foton találkozik a detektor egyik elektronjával, akkor nemcsak a rezonancia feltétel határozza meg, hogy okoz-e a foton elektron átmenetet, hanem az is, hogy az elektron állapotának fázisa egyezik-e a foton fázisával.

Kvantált elektronállapotok atomokban

Amikor elektronpályákat rajzolunk fel az atommagok körül szintén képzeletünkre hagyatkozunk. A bolygók pályájáról a Nap körül folytonos információval rendelkezünk, hiszen folytonosan érkeznek hozzánk az onnan visszaverődő fotonok. Az elektronpályákról akkor szerzünk tudomást, amikor az elektron az egyik pályáról egy másikra kerül. Mindig csak ugrásokat látunk, de az állandó, úgynevezett stacionárius pályák rejtve maradnak előlünk. Rajzolhatunk szép ábrákat, amelyben bemutatjuk az egyes pályák eloszlását az állapotfüggvényt meghatározó kvantumszámok alapján. A pálya-impulzusnyomatékot jellemző kvantumszám, ha nulla (s-pálya) akkor gömbszimmetrikus pályát rajzolunk fel, ha L = 1 (p-pálya), akkor a magban összefutó két lebeny tünteti fel az eloszlás alakját, hasonlóan ábrázolhatjuk a magasabb kvantumszámú eloszlásokat is. De az már hibás elképzelés, ha rákérdezünk, hogyan mozog az elektron a pályán belül. Például az L =1 p-pályák az atommagban nulla valószínűséggel fordulnak elő és nem kérdezhetjük meg, hogyan közlekedik az elektron a két lebeny között. Amikor az elektron pályán belüli mozgásáról beszélünk ismét egy gondolkozási csapda rabjai lettünk, mert az elektron pályafogalma is csak képzeletbeli és nem valóságos. A kvantummechanikai valószínűség nem fejez ki többet, mint nem-tudásunkat a valódi pályáról. Az elektron „mozgása” nem a klasszikus tér és idő dimenziókban történik, hanem a térben értelmezett valószínűségi mezőben. Ezt az elképzelést mutattam be egy elképzelt párbeszéddel az elektron és a fizikus között: lásd „Az intelligens elektron” című bejegyzést.

A gondolkozási csapdák elkerülése

A kvantummechanika valószínűség fogalma gyakran teszi próbára logikánkat, amikor a makrovilág fogalmaival akarunk valamit megérteni. Ilyenkor a legjobb, ha elgondolkozunk rajta, hogy a vizsgált jelenségből mi az, ami valódi, azaz tényleges megfigyeléseken alapul,és mi az amit képzeletünk, vagy matematikánk tesz hozzá, hogy összekösse a megfigyeléseken alapuló fogalmaink között tátongó hézagokat..Ha elválasztjuk egymástól a valódi és a képzeletbeli fizikai világot, akkor esélyünk van rá, hogy ellentmondásmentes világképet alkossunk.

A blog egyéb írásait összegzi és megadja a linkeket a „Paradigmaváltás a fizikában” című bejegyzés

Dr. Balogh Sándor: Einstein tér/mező kérdésének megoldása c. könyve

A tudomány hajótörése

Dr. Balogh Sándor Újvilágba szakadt honfitársunk idén jelentette meg művét, Einstein tér/mező kérdésének megoldása (Egy új világkép alapjai) címmel, a Magyarságtudományi füzetek sorozatában, mint 27. sz. kisenciklopédiát. A könyv kiadását a Magyarok Világszövetsége vállalta. Az Előszót maga Petrubány Miklós István Ádám, a Világszövetség elnöke írta. A munka a Magyarok IX. Világkongresszusára időzítve jelent meg.

Balogh Sándor szinte minden tudomány-területet érint könyvében: a fizikát, a mérnök-tudományt, a kozmológiát, a geometriát, a biológiát, az ismeretelméletet, a filozófiát, sőt a teológiát is.

Így foglalja össze a ma divatos paradigmát (világképet, világmagyarázatot). E paradigma 1. materia­lista, vagyis azt vallja, hogy csak anyag létezik, 2. pozitivista, vagyis csak empirikus mód­­szert ismer el: csak az tanulmányozható, ami látható vagy tapintható, 3. a dimenziókat csak a térre vonat­koztatja, és csak három dimenziót ismer, 4. redukcionista, vagyis a tényeket mindig ala­cso­nyabb dimenzióra vezeti vissza (pl. a szellemit az agy-tevékenységre), és amely jelen­sé­geket nem képes redukálni, azokat egyszerűen kizárja a tudományokból, 5. a lentről felfelé való fejlődésben hisz, intelligens okozást nem fogad el, 6. a magasabb szintek csak a véletlen alapján állnak elő, 7. determinista, 8. ateista, 9. (ugyanakkor) a legkisebb anyagi léte­zőt tekin­ti afféle „isten-részecskének”, ezt keresi, ebben látja a világ végső magyarázatát, a világ sze­rin­te „isten-részecskék” halmaza. 10. Épp ezért e világlátás szerint a tudomány összeférhetetlen a val­lással.

Hogy mennyire vallás-ellenes ez a paradigma, nos, már itt érdemes utalni rá: az „intelligens tervezés” elméletét (az evolucionizmussal szemben) azért utasítottta el teljes erővel a tudományos közvélemény, mert olyan elemet feltételezett az okok sorában, amely túlfeszíti a mechanikus okság körét: az isteni okságot. Tudjuk, az USA-ban nem is szabad tanítani a teremtés.-elméletet, mert az, úgymond, ellenkezik az amerikai alkotmánnyal, abban pedig mintegy dogmaként szerepel a fejlődés-elmélet.

Ez a világmagyarázat azonban Balogh szerint válságba került, útja hajótörést szenvedett. A válságért Balogh szerint az okság beszűkített szemlélete a felelős. Arisztotelész még négyfajta okot ismert: az anyagi, a formai, a ható- és a cél-okot. Ezek közül a materialista szemlélet csak a ható-okságot ismeri el. Ismeretelméletileg pedig csak az érzéki ismereteket. És igaz ugyan, hogy Szent Bonaventura is azt írta: „Semmi sincs az értelemben, ami előbb nem volt az érzékekben”, de hozzá tette: „sok olyasmit is megismer az ember, amit sohasem látott, s miután látott valamit, sokat gondolkodik rajta és következtet belőle”. A valóság nem fér bele a tapasztalhatóba, a kézzel-foghatóba. Az élet megnyilvánulása, és főleg a tudati vagy épp a parapszichikai jelenségek szétfeszítik az anyagi okság körét. Balogh külön is hangsúlyozza: a láthatóság és a tapinthatóság nem létkérdése a valóságnak, hanem csak jellegzetessége bizonyos anyagi mezőknek, tehát láthatatlan és tapinthatatlan létezőkre is számítani kell. Ami pedig az „isten-részecskék” megtalálását illeti, ez az elképzelés hiú ábrándnak bizonyult. Ma már sokan úgy vélik, „anyagi részecske” egyáltalán nem is létezik, mert az anyaginak ismert világ lényegében hullámokból áll.

A válság a „legtudományosabb” szakág, a fizika területén is jelentkezett. A kvantumfizika szerint kétfajta elemi részecske létezik: a fermion és a bozon, és négyfajta erő: a tömeg­vonzás, az elektromágnesesség (az EM), az erős és a gyenge hatás az atomok világában. A gond az, hogy ezek a jelenségek nem hozhatók „egy fedél” alá. Az elektromágneses jelenség nem áll részekből, a tömegvonzás és a gravitáció viszont a tömeg egyik tulajdonsága, „kvantált”, részekre bontható. Amellett az EM hatás polarizált, a gravitáció viszont egy­pólusú, tehát nem lehet közös az eredetük. Ugyanez érvényes az atomon belüli hatásokra és kölcsönhatásokra is.

Épp ezért sokan már új, átfogó elmélet létrehozását követelik. Ez lenne a „Theory of Everything”, a ToE, vagyis a Mindent Magába Foglaló Elmélet. Vezéralakja Stephen Hawking fizikus. aki az alábbi problémák megoldását várja a ToE-től: 1. adjon olyan modellt, amely egyesíti az erőket és részecskéket, 2. adjon választ arra kérdésre, milyen volt a világ­egyetem állapota az idő kezdete előtt, 3. magyarázza meg, a világ miért olyan, amilyen, 4. és főleg: egyesítse sikeresen az általános relativitás elvét a kvantumfizikával.

Azonnal láthatjuk – mondja Balogh – hogy ilyen elméletet felállítani lehetetlen. Például: hogyan magyarázzuk meg, milyen lehetett a világ a Nagy Bumm előtt, ha kizárjuk a teremtést? Ami pedig a szélső értékek egyesítését illeti, a probléma éppen az, hogy a kvantummecha­niká­nak a relativitás­elmélettel való összeházasítása nemcsak hogy nem oldotta meg a problé­mákat, hanem súlyos­bította azokat, a japán származású amerikai fizikus, Michio Kaku szerint. Balogh Sándor az Einsteinnel szemben táplált nem kis szimpátiája ellenére elismeri, hogy ezért a válságért jórészt éppen Einstein volt a felelős. Ugyanakkor utal arra is, hogy Einstein már 1952-ben kimondta a korábbi paradigma válságát, és új világmagyarázat kialakítását sürgette.

Einstein éles vitába keveredett Max Bornnal, aki az anyagi részecskék rendjét az ún. statisz­tikai értelmezéssel magyarázta. Erre vonatkozott híres mondása: „Isten nem kockajátékos”. De ugyanígy nem fogadta el Gavid Bohr koppenhágai iskoláját sem, amely látszat-világig, a realitás tagadásáig jutott el. David Lindley szerint ez a vita a 20. század egyik legdrámaibb, intellektuális csatája volt. Nick Herbert még tovább haladt ezen az úton. Szerinte a világot a megfigyelő alkotja, sőt az (emberi) tudat teremti meg a világot. Ez nyílt szubjektív idea­lizmus. Ezen a ponton jelentkezett az az elmélet is, hogy egy vagy több párhuzamos világ­egyetem létezik. Mindez Balogh szerint átfogó eszmei zűrzavarhoz vezetett.

A hagyományos világkép válsága és csődje miatt új paradigma kialakításának szüksége vetődött fel. Az első, erre vonatkozó kísérlet a holisztikus paradigma volt. A holisztikus világképet elsőként Fritjof Capra dolgozta ki. Szerinte a hagyományos paradigma hibája az volt, hogy lentről felfelé haladva építette fel a világot. Tehát abból indult ki, hogy a bonyolult rendszereket szét kell bontani, alkotó elemeire, és azokból kell az egészet összerakni. Ez a törekvés Démokritosszal kezdődött (vö. a-tomosz, tovább már nem bontható részecske) és napjainkig tart, az egész, eddig tárgyalt klasszikus paradigmának ez az alapja. Capra szerint nem a részből, hanem az egészből kell kiindulni. Ahogy egy gépezetben, vagy akár egy élő szervezetben is a részeknek csak az egészben van értelme, a rész önmagába csak selejt és ócskavas, úgy a kozmosz és a természet is holisztikus, részei az Egész felől válnak érthetővé.

A holizmus kialakításához Capra és mások a távol-keleti, panteista vallásokból merítettek ihletet. A kínai filozófia egyik ága, a taoizmus adott itt új impulzusokat. Ebben a világképben eltűnnek a kvantumfizika anomáliái, az egymástól távollevő anyagi részecskék egymásra hatása, a távolba hatás érthetővé válnak. A materialista modell szerint az okság elve csak ott képes működni, ahol térben és időben folytonosság van jelen, a tárgyak csak egymásra hatva képesek működni. Ha valahol szakadék vagy hézag támad, az okság nem tud érvényesülni. A holisztikus modellben minden mindennel összefügg. A részecskék a látható rendben szétvá­lasztva léteznek, de összefüggenek a rejtett rendben.

Paul Davies szerint napjainkra belátható, hogy kétféle világrend létezik. A valóság egyik fele redukcionista módon, másik fele pedig holisztikusan magyarázható. Balogh Sándor szerint azonban ez a tudathasadásos állapot nem tartható fenn. Rámutat: Capri a keleti misztiku­sokhoz hasonlóan – elveti a tér és az idő fogalmát, ez azonban az okság fogalmának elvetését is feltételezi, és ez teljes káoszhoz vezet. Mind a korábbi, mind ez a paradigma önálló, teljes világ­képet feltételez, a kettő nem létezhet együtt.

A holisztikus paradigma mégis fontos tanulságot tartogat számunkra – mondja szerzőnk. Mégpedig, hogy a redukcionista, materialista világkép tarthatatlan. Ha viszont sem egyik, sem másik nem ad teljes magyarázatot, szükség van egy harmadik paradigmára, amely mindkét oldalt magába foglalja, és ez Balogh szerint a hierarchikus, pluralista paradigma.

A ponttól a négydimenziós térig

Az új paradigma alapjait Einstein 1952-ben rakta le. Írása annyira szembement a hagyo­mányos világképpel, hogy szaklapok nem is közölték le, esszé-gyűjteményének csak 15., 1954-ben megjelent kiadásában jelenhetett meg, mint 5. Függelék. Ebben így foglalja össze, mit is javasol kiútként, megoldásként: 1. Nincs üres tér, hanem a tárgyaknak van térbeli kiterjedése, 2. amit görbült térnek ismerünk, az egyfajta mező, 3. a gravitációs mező szabályai kiterjeszthetők egy általános mezőelméletre, 4. a fizikai valóságot, mint mezőt kell felfogni, négydimenziós térben, 5. a mezőnek struktúrája, szerkezete van. Mindehhez hozzáteszi: meg kell szüntetni a tabukat a tudományokban.

Nagy példaképe arcképét nem véletlenül helyezte könyve címlapjára. Einsteinnek nem adatott meg, hogy az új paradigmát részleteiben is kidolgozza, alapeszméit Balogh professzor gondolta tovább. Így elméletét joggal nevezi, és nevezhetjük mi is Einstein-Balogh paradig­mának.

Szerzőnk az új paradigma megértését a valóság geometriájának leírásával kezdi; a geometria egyik kedvenc tudománya. Hogyan is tudjuk Euclides óta? Létezik pont, egyenes, sík és tér, Ám az egyenes fraktálos, vagyis szaggatott, és a szakaszokból sohasem kapunk kerek egészet (1-es értéket), csak a pont mozgatásából. És viszont csak a sík metszetéből (egy felsőbb dimenzióból) nyerhetünk egyenes vonalat. Ugyanígy síklapot csak a három dimenziós térből hasíthatunk ki. Az elv tehát az, hogy részekből sohasem kapunk egészet, az egész mindig több a részek egységénél. Végső soron ahhoz a metafizikai elvhez jutunk el, hogy az ok csak magasabb rendű okozó lehet.

Az egész és a részek viszonyát jól példázzák a kristályok. Polányi Mihály leírja: az alkotó részecskékből 230 féle kristályszerkezet jöhet létre, de egyik sem magyarázható meg az egyes molekulák természetével. Így van ez a gépek, és még inkább az élőlények esetében. Mindenki ismeri a vízmolekulát (H₂O), de jól tudjuk, hogy a két összetevő tulajdonságaiból nem lehet megmagyarázni a víz valóságát. Balogh hozzáteszi: ha megtalálnók az „isten-részecskéket”, és összeraknánk őket, akkor sem kapnánk meg az anyag természetét.

De vajon mi a helyzet a háromdimenziós térrel? A fenti logikát követve a három kiterjedésű teret is csak egy magasabb dimenzióból fejthetjük meg. A közvélemény azt tartotta, hogy ez a negyedik dimenzió az idő. De míg az alsóbb dimenziók mind úgy jönnek létre, hogy egy adott vonalra merőlegeset húzunk, aztán arra is egyet, és még utóbbira is egyet, az idő nemcsak az egyik vagy másik egyenesre merőleges, hanem mindegyik dimenzióra. Más szóval nem térbeli dimenzió.

Nos, Einstein 1952-ben feladta az „üres tér” fogalmát. Ha a térbe egy testet helyezünk el, az már szétfeszíti az (üres) három dimenziós teret. Szerzőnk levonja a következtetést: nem a tér lesz négy dimenziós, hanem a tárgy! Szerinte ez a negyedik dimenzió két részre osztható: a belső és a külső valóságra (ana és kata-oldalra). A belső valóság kétfajta mezőt tartalmaz: az anyagi és a morfogenetikus mezőt (a morphé=forma és geneszisz=létrejövés szóból). Az arisztotelészi-szenttamási metafizika kifejezéseivel ez a kettősség az anyagi és a formai elvnek (causa materialis et formalis-nak) felel meg. Az arisztotelészi hilemorfizmus ma így hangzik: minden anyagi tárgy ős-anyagból és formát adó mezőből áll, más szóval: a világ energiakvantumokból és különböző fajtájú és szintű morfogenetikus mezőkből épül fel. A morfogenetikus mezőben a forma-elv mellett a cél-ok tulajdonságait is hordozza: időben később válik valóra, de már ott hat egy folyamat elején. A DNS információ-köteget és célprogramot hordoz!

Balogh látásmódja szerint a tárgyak külső valósága sugárzó erők hálózata és láthatatlan információs mezők tömege, mint majd látni fogjuk. Mindebből most a morfogenetikus mező a legfontosabb. Nemcsak az atomokat, kristályokat határoz meg a forma-elvük, hanem a sejtek működését, vagy pl. a megtermékenyített petesejt fejlődés-sorát. A morfogenetikus mező egy csoport sejt, amely képes reagálni konkrét, helyi biokémiai jelekre, ami további morfológikus struktúrák vagy szervek kialakulásához vezet. Különösen az agy működésében tölthet be ez az elv felmérhetetlen szerepet. Balogh szerint a lélek, mint forma-elv, munkálkodik a fogamzás pillanatától a halálig (vagy épp azon túl), és ezt az emberre vonatkoztatva a legfelső morfogenetikus mezőnek tekinti.

Rupert Sheldrake, a mezőjelenségek egyik úttörője, a morfogenetikus mező fogalmát kiterjesztette a kata-valóságra, vagyis az egyedek, sőt fajok egymás közti viselkedésére is. Szerinte, ha egy faj elsajátít egy új viselkedésmintát, ez megváltoztathatja az adott faj oksági mezejét, és ha e viselkedés elég sokáig ismétlődik, akkor morfogenetikus rezonancia alakul ki, amely kihat az egész fajra.

Sőt Shaldrake azt is felfedezte, hogy egyes állatok természeti jelenségekre is előre reagálnak, rezonálnak, pl. megérzik a földrengés vagy a cunami közeledtét, mikor minderre még semmilyen jel nem mutat. Az egyes fajokról ez az érzékenység átragadhat a másikra is, mintegy közös morfikus mező részei. Úgy tűnik, még a növényeknek is van efféle resgézmezője, gondoljunk pl. a bab, a borsó, a szőlő kapaszkodó kacsaira.

Összefoglalva elmondhatjuk: még a „leganyagibb” struktúrákban, mint a kristály vagy a mágneses erőtér, jelen vannak láthatatlan (nem-anyagi?) stuktúrák, amelyek az anyagi részecskéket szervezik, irányítják, rendszerbe foglalják. A morfogenetikus mezők hierarchikus rendbe ágyazódnak, ahol mindig a felsőbb mezőből válik érthetővé az alatta lévő mező, és így tovább. Ebben a rendszerben az anyagi, materiális világ a valóságnak csak mintegy „oldallapja”, elenyésző hányada.

De immár elkerülhetetlen annak a kérdésnek a megválaszolása, mi is az a mező (field). Balogh idéz néhány meghatározás-kísérletet. Prigozsin orosz kutató szerint a mező rezgésekből álló valami, vagyis hullám. De vajon mi az a hullám? – kérdezi szerzőnk. Leon Ledermann, Nobel-díjas fizikus szerint a mező a térnek az a tulajdonsága, hogy valamely forrásból eredő hatás ne tudja megzavarni. Ez túl negatív megközelítés, mondhatnók. Balogh definíciója: a mező érzékszerveinkkel nem tapasztalható, de különféle, a háromdimenziós világban való hatásaiból felfedezhető és megismerhető közeg, amely képes a különálló tárgyak (részek) között kapcsolatot teremteni a térben, akár távolba hatás révén is.

Balogh fontosnak tartja, hogy a mezők hierarchikus rendbe szerveződnek. Ahogy egy-egy mező szelencéjét mindig csak „felülről” lehet kinyitni, értelmezni, úgy a mezők rendszerét is. A magasabb létrendből mindig bele lehet látni az alacsonyabba, az okság elve csak fentről működik, akár úgy is, hogy a felső szint felfüggeszti agy alsóbb működését. Az okok sorának legelején – vagy épp csúcsán – Isten áll, mint Első Mozgató – vallja Balogh Sándor.

Mint olvasója, szinte minden elgondolásával, következtetésével egyetértek. Talán csak egyetlen ponton kelnék vele vitára. Több helyütt a lelket, sőt Istent is a mező kategóriájába sorolja. Helyesebb volna talán, hogy lételméletben, ontológiában gondolkodnánk. A mezők nem egyszerűen „közegek”. A közeg még mindig odatapad a valóság anyagi oldalához. Sőt maga a „mező” szó is. Talán érdemes lenne létformákról beszélni, a lét különböző síkjairól, dimenzióiról, amelyek a létteljesség, az Abszolút Értelem és Akarat, mint Programozó elgondolásait és akaratát hordozzák.

Dr. Cselényi István Gábor

A blog további írásainak összefoglalása a linkekkel együtt megtalálható a „Paradigmaváltás a fizikában” című bejegyzésben

Hogyan hozhatunk létre teleportálást a kvantummechanika szerint?

Sokunknak megfogja a fantáziáját, hogyan kerülhetnénk át valahová a világ más szegletébe, anélkül hogy oda kellene utazni, vagy ha mi nem is tehetjük ezt meg, hogyan küldhetnénk át egy tárgyat valahová közvetlenül. Ezt hívjuk teleportálásnak. Van a kvantummechanikának egy értelmezése, amit összefonódott kvantumállapotnak hívnak, ami felveti ennek lehetőségét. Talán nem csak a sci-fi világában valósítható meg a teleportálás? Ezt a kérdést járom körül ebben a bejegyzésben rámutatva az összefonódott kvantumállapot körüli vitákra és a lehetséges megvalósítás esélyeire.

Az EPR paradoxon

Az összefonódott kvantumállapot lehetősége az EPR paradoxon körül kialakult vitából indult ki, amit Einstein, Podolsky és Rosen nevezetes publikációja váltott ki. A kérdésről már írtam az „Einstein igazsága és tévedései” című bejegyzés második részében, amiből néhány gondolatot itt is átveszek.

A kvantummechanikai valószínűség és a rejtett paraméterek

A huszadik század elejének fizikai felfedezései forradalmat indítottak el nem csak a fizikában, hanem egész gondolkozásunkban. A kvantummechanika ugyanis rést ütött determinisztikus világképünkön, amikor azt állította, hogy bizonyos folyamatok bekövetkezésére, vagy egyes mérések eredményére csak valószínűségi kijelentéseket tehetünk bármennyire is törekszünk a körülmények legpontosabb meghatározására és reprodukálására. Példaként gondoljunk a fényre, amikor az üveglapon áthalad. A fény 4 százaléka visszaverődik és 96 százaléka megy át az üvegen. A problémát a foton fogalma hozza magával, ami a modern fizika szerint a fény legkisebb egysége. Ha most elképzelünk egyetlen fotont, az hogyan dönti el, hogy visszaverődik, vagy áthalad? Kell lenni valamilyen egyedi szabálynak, ami sok-sok foton esetén létrehozza a tapasztalt statisztikai arányokat. Einsteint is foglalkoztatta ez a probléma és feltette magának a kérdést: mi határozza meg az egyes fotonok sorsát különböző kísérletekben? Erre vonatkozik nevezetes kiszólása is: „Az Isten nem kockajátékos”. Kétségeit fogalmazta meg két szerzőtársával együtt felvetve a „rejtett paraméterek” lehetőségét. Ez alatt azt értette, hogy van valamilyen rejtett, azaz a kvantummechanikában nem szereplő paraméter, amely szabályozza az egyes fotonok sorsát és eldönti, hogy mi következik be, amikor a foton valamivel kölcsönhatásba kerül.

Bell álláspontja az EPR paradoxonról

A vita máig sem került nyugvópontra, sok érv hangzott el a rejtett paraméterek lehetősége mellett és ellen, bár mára inkább az utóbbit tartják helyesnek. Ebben nagy szerepe van Bell megállapításának, aki a részecskék, illetve a fotonok polarizációs tulajdonságai alapján vonta le következtetését.

Mit értünk a foton polarizációja és a hullámfüggvény redukciója alatt?

Ejtsünk néhány szót a polarizációról, hogy értsük miről is van szó! Képzeljünk el egy nyilat, amelynek orientációját akarjuk meghatározni a mágneses mező által kijelölt irányhoz képest. A kvantummechanika azonban csak két irányt enged meg: lehet párhuzamos, vagy ellentétes irányú a mezőhöz képest, amikor elvégezzük a mérést. Legyen ez a két irány a „fel” és a „le”. De mielőtt a mérést elvégeznénk ez a nyíl különböző irányú lehet, amire csak valószínűségi kijelentéseket tehetünk. A kvantummechanikában ezt a valószínűséget a részecske, vagy foton állapotfüggvénye határozza meg. Mi az a folyamat, ami az előzetes sokféleségből kiválasztja akár a „fel”, akár a „le” állapotot? Ez egy másik interpretációs kérdés, ami végighúzódik a kvantummechanika történetén. A fizikusok többsége által elfogadott magyarázatot nevezik koppenhágai felfogásnak, amely szerint a mérés „redukálja” a hullámfüggvényt, azaz tényleges állapotváltozás következik be. Ezt jegyezzük meg, mert ennek fontos szerepe lesz a teleportálás kérdésében!

A rejtett paraméterek szerepe

Miből indul ki Bell érvrendszere? Megnézte, hogy a kvantummechanika fogalmi világával összeegyeztethető-e egy olyan rejtett paraméter létezése, amely minden időpillanatban és minden helyen pontosan determinálja a részecske sorsát, azaz jelen esetben meghatározza a nyíl pontos irányát. Végezzünk el különböző méréseket, amikor kétféle, egymásra merőleges irányban orientáljuk a mágneses mezőt. Ha a nyíl pillanatnyi iránya közel van a „fel” orientációhoz, akkor nagyobb valószínűséggel detektáljuk a műszerrel a „fel” állapotot, ellenkező esetben viszont a „le” állapot bekövetkezése lesz a valószínűbb. Ebből a rejtett paraméter által diktált képből bizonyos valószínűségekhez jutunk. Bell ezt összevetette a kvantummechanikából származtatott valószínűségekkel és ellentmondásra jutott. Ezt fejezi ki egy egyenlőtlenség formájában, amelynek végső konklúziója: a kvantummechanika összeegyeztethetetlen a rejtett paraméter létezésével. Aki ennek matematikájára is kíváncsi, annak ajánlom figyelmébe Geszti Tamás kitűnő könyvét: „Kvantummechanika”, (Typotex, 2014).

Az Aspect kísérletek és az összefonódott részecskeállapot

Voltak akik nem álltak meg az elméleti okfejtésnél, hanem konkrét kísérleteket végeztek el, közülük volt az első a francia fizikus Allen Aspect  (A vonatkozó irodalmi hivatkozások megtalálhatók az „Einstein igazsága és tévedései” bejegyzés második részében). Olyan kísérleti elrendezést hoztak létre, amelyben mindig egyidejűleg két foton jött létre es ezek polarizációját vizsgálták két ellentétes irányban egyenlő távolságban a forrás helyétől. Az egyidejűleg keltett fotonok polarizációja ellentétes a megmaradási törvények miatt, és evvel egyezésben valóban ellentétes polarizációt figyeltek meg a két különböző műszeren. A nyert eredmény ellentmondott Bell kvantummechanikai következtetéseivel. Mi lehet ennek az oka? Csak nem a kvantummechanika rossz, ami pedig olyan kiváló leírást ad a mikrovilág folyamataira? Erre a választ egy új kvantummechanika fogalom bevezetése hozta meg: az összefonódott állapotoké. Amikor két fotont létrehozunk, valójában a fotonok nem válnak igazán szét, vagyis bizonyos értelemben szétválnak, de mégis együtt maradnak! Érdekes, hogy a kvantummechanikáéban milyen gyakran köszönt vissza Mátyás Király és az okos lány története, aki adott is ajándékot, meg nem is.

A térben kiterjedt kvantumállapot

A magyarázatok szerint a két-fotonos állapotot egyetlen állapotként kell kezelni, és amikor az egyik foton polarizációját meghatározzuk, az magával hozza a másik foton polarizációjának megváltozását. Ez a változás tehát teljes bizonyossággal megtörténik és nem csupán bizonyos valószínűsége van, mint azokban a számításokban, amikor külön-külön vesszük figyelembe a fotonokat. Itt kapcsolódik be, amit korábban írtam a koppenhágai felfogásról: amikor mérjük az egyik irányban a polarizációt, avval tényleges állapotváltozást hozunk létre az egyik irányban és ez szintén tényleges változást idéz elő a másik helyen. Ez tehát a részecske polarizációs állapotának teleportálása, ami ráadásul nincs korlátozva a fénysebesség által, mert azonnal bekövetkezik. Ennek oka, hogy nem pontszerűen lokalizált kvantummechanikai rendszerről van szó, hanem térben kiterjedt objektumokról. Aspect kísérletében még csak néhány méter választotta el egymástól a két mérőhelyet, de az újabb fényvezetőket alkalmazó eljárásban ezek már több kilométerre vannak egymástól.

Hogyan működik a kvantum teleportálás?

Ha elfogadjuk a fenti magyarázatok helyességét, akkor feltehetjük a kérdést, hogy milyen teleportálást lehet elvégezni? A probléma az, hogy az összefonódott állapotok csak rendkívül kis számban léteznek, és ha egy ilyet detektálunk, akkor sem tudjuk, hogy ennek hatása hol fog megjelenni. Emiatt nem kerülhető el, hogy legyen egy központi „adó” és legyen két mérőhely, amelyek között a teleportálás végbemegy. A legkönnyebb összefonódott foton-párt létrehozni és a jelet továbbítani üvegszálakon, ahogy a jelenlegi kísérleteket is megvalósítják. A kétféle polarizációs állapot mint a digitális technika bitje fogható fel, ezért kellő számú kísérlettel az „A” helyen létrehozott kép átvihető a „B” helyre, ahol annak tükörképe jelenik meg. Földi körülmények között ez a technika nem jár előnyökkel, de ha például a Mars és a Föld között akarunk késleltetés nélkül kapcsolatot létrehozni, ez hasznos lehet a marsjáró földi vezérlése esetén. Ez a teleportálás elvben megvalósítható, bár nagy kérdés, hogyan lehet a két bolygót üvegszállal összekötni és ilyen hosszú távon biztosítani, hogy az információ az üvegben való veszteség miatt ne vesszen el.

Bármilyen anyag teleportálása ennél lényegesen nehezebb feladat, mert ekkor az elektronok és nukleonok összefonódott állapotát kellene létrehozni. Elvben létrehozhatunk ilyen elektron-pozitron, vagy nukleon-antinukleon párokat, de ekkor a teleportált objektum mint antianyag jelenik meg a túloldalon. A technika elvben kisebb molekuláknál működhet, de nagyobb objektumoknál olyan sok elektront és nukleont kellene átvinni, ami lehetetlennek tűnik. További probléma, hogy biztosítani kellene, hogy az összefonódott részecskék ne ütközzenek a levegővel. Ezért a teleportálás csak a világűrben, vagy légüres térben oldható meg.

Szubjektív vélemény az összefonódott állapotok létezéséről

A teleportálás bemutatásánál feltételesen írtam, hogy akkor lehetséges, ha helyes az összefonódott állapotok kvantummechanikai koncepciója. Szerintem ez is megkérdőjelezhető, bár ez a véleményem nem találkozik a fizikusok többségének felfogásával. Éppen ezért az olvasót figyelmeztetem, hogy a következő okfejtésemet kellő gyanakvással fogadja.

Az irány fogalmának különböző arcai

Bell gondolatmenetének kritikus pontja, amikor úgy értelmezi a rejtett paramétert, hogy az minden időben és helyen egyértelműen definiálja a polarizációs fázist. Szerintem erre nincs szükség, az említett Aspect kísérletekben elegendő a két foton fáziskülönbségének meghatározottsága, márpedig a megmaradási elv szerint a két fázis épp ellentétes egymással. Az elektrodinamika szerint a fázist mutató nyíl a foton frekvenciájával körbejár, ezért ha a forrástól egyenlő távolságban végzünk méréseket, akkor a két foton fázisát mindig ellentétesnek kell találni. De miért nem határozza meg ez a kép a polarizációs irányt a térben? Ennek oka, hogy ha nincs kölcsönhatásban a foton, vagy beszélhetünk elektronról, vagy más részecskéről is, akkor nincs értelme az irány fogalmának. Mi természetesen irányokban és távolságokban gondolkozunk, mert így tudjuk rendszerezni a minden pillanatban szemünkbe érkező hatalmas mennyiségű információt. De a kölcsönhatás nélkül haladó foton fázisát nem lehet semmilyen térbeli iránnyal összevetni, ezért amikor leírjuk a foton viselkedését, akkor helytelenül járunk el, ha a szokásos térben képzeljük el. Van viszont egy nagyszerű matematikai módszerünk, a kvantummechanika, amely áthidalja a fogalmi különbségeket. Ha nincs értelme az iránynak, akkor bevezeti a valószínűség fogalmát, például azt mondja, hogy minden iránynak azonos a valószínűsége és ezt tükrözi a mikrorészecske hullámfüggvénye. De mi történik a méréskor, mikor meghatározzuk a polarizációs irányt a mágneses mező által kijelölt irányhoz képest? Ekkor már elnyeri valódi értelmét az irányfogalom, hiszen látjuk a mágneses pofa síkját, onnan hatalmas számú foton jut el a szemünkbe. Tehát amikor a polarizációs irány meghatározásáról beszélünk, akkor nem csupán a műszerünk által szolgáltatott információra szorítkozunk, hanem arra is, amit mi magunk a műszerről, például a mágneses pofa irányáról tudunk. Amikor azt mondjuk, hogy a mérés „redukálja” a hullámfüggvényt, akkor ez nem a fizikai állapotváltozással függ össze (persze az is bekövetkezik, mert nem mérhetünk úgy, hogy a kölcsönhatás ne változtatná meg a rendszer állapotát), hanem az igénybe vett információnk bővül ki a műszerről nyert képünkkel.

Létrejöhet-e a fénynél gyorsabb kölcsönhatás?

Az Aspect típusú kísérletek értelmezéséhez emiatt nincs szükség az összefonódott kvantumállapot fogalmára, nem kell arra gondolnunk, hogy az egyik foton polarizációjának megváltoztatása magával hozza a másik fotonét is. Az „A” és „B” pontokon mért polarizáció azért kapcsolódik össze, mert a két foton fázisa mindig egymásnak fordítottja, ha a mérés a forrástól azonos távolságban kerül sorra. Tehát a fázisok egyértelmű relatív viszonya megvalósul összefonódás nélkül is. Éppen ezért a két fázis meghatározása nem két különböző kvantummechanikai esemény, így nem sérülnek a kvantummechanika törvényei.

Mit tudunk ezek után mondani a teleportálásról?  Valójában nem arról van szó, hogy az „A” pontból információt küldünk át a „B” pontba, hanem arról hogy az „A” pontban nyert ismeret alapján azt is tudjuk, hogy mi történt a „B” pontban ugyanakkor. Ez azt is jelenti, hogy a marsjárót nem tudjuk késleltetés nélkül irányítani a Földről, de legalább megtudhatjuk, hogy a központi „adóból” odaküldött foton éppen milyen fázisban érkezett oda. Ennek a magyarázatnak előnye, hogy nem kerül szembe a relativitáselmélet főszabályával sem, amely megtiltja, hogy a tér két pontja között rövidebb idő alatt jöjjön létre kölcsönhatás, vagy információcsere, mint amennyi idő alatt a fény bejárja ezt az utat.

A blog egyéb írásait összegzi és megadja a linkeket a „Paradigmaváltás a fizikában” című bejegyzés

Ha feldobunk egy követ, akkor a kezdeti lendület felfelé viszi, majd a haladás lassulni kezd, majd megáll és gyorsulva esik lefelé, ha fellövünk egy rakétát kellő sebességgel, akkor nem zuhan vissza, hanem elszakad a Földtől, de azt is megtehetjük, hogy vízszintes pályára álljon és keringjen Földünk körül. Mindegyik esetben a mozgási energia és a gravitáció potenciális energiájának egymásba alakulása írja le a folyamatot. Sokkal nagyobb méretekben is hasonló jelenség játszódik le az Univerzumban az ősrobbanás után.

A szökési sebesség

Nézzük először a földi példát, hogy könnyebben értsük az Univerzum korszakváltásait. Ha az m tömegű rakétát  v sebességgel lőjük fel, akkor a kinetikus energia ½ m.v² lesz. Az R = 6378 km sugarú Föld felszínén a potenciális energia V = G.m.M/R, ahol G = 6,67x10^-11.m³/s²kg az általános gravitációs állandó és M = 5,97x10²⁴ kg a Föld tömege. A rakéta elszökik a Földről, ha kinetikus energiája meghaladja a potenciális energiát, azaz

½ m.v² > G.m.M/R

ahonnan a szökési sebesség v = 11,1 km/s a v² = 2G.M/R összefüggés alapján. A pályára állítás sebessége ennél kisebb (7,86 km/s), amit a centrifugális erő és a gravitációs vonzóerő egyensúlyából számolhatunk ki:

m.v²/R = G.m.M/R² , azaz v² = G.M/R

Az Univerzum lehetséges modelljei

Az Univerzum kialakulása az ősrobbanás után természetesen ennél bonyolultabb jelenség. A hasonlóság annyi, hogy ekkor is három alapszcenárió lehetséges: a táguló, az összehúzódó és az egyensúlyi modell. A lehetséges modellek szempontjából az  M tömeget az Univerzum teljes tömege, illetve homogén rendszert feltételezve annak sűrűsége képviseli, míg további fontos szerepet játszik az Univerzum teljes kiterjedésének „A” sugara.

Einstein gravitációs egyenlete

Mielőtt az Univerzum fejlődését tárgyalnánk, először lépjünk vissza az időben, amikor Einstein kidolgozta gravitációs elméletét. Ő a gravitáció eredetét a tér görbületével hozta kapcsolatba: szerinte a tömeg maga körül begörbíti a teret és emiatt nem az egyenes út lesz a mozgás legrövidebb útja, hanem az a trajektória, amely a görbületeket mentén halad. Einstein, amikor a csillagos égre nézett, úgy képzelte, hogy amit látunk az ősidők óta hasonló, bár a csillagok és galaktikák egymáshoz képest vándorolhatnak, de sűrűségeloszlásuk alapjába véve változatlan. Ebben az értelemben egyensúlyi világképben gondolkozott. De miért nem zuhan önmagába az Univerzum a gravitáció miatt, vagy miért nem szalad szét a benne rejlő kinetikus energia miatt? Azaz elgondolás, hogy az egyensúlyt a keringő mozgások miatti centrifugális erő tartja fent nem volt számára elfogadható, mert akkor a távoli galaxisok sebessége messze meghaladta volna a fény sebességét, ami pedig a speciális relativitáselmélet kiinduló pontja. Ezért gondolt egy merészet és feltételezte, hogy a térnek van egy immanens antigravitációs hatása, ami egyensúlyt alkot a gravitációval és létrehozza az „örök” Univerzumot. Ezt az elképzelést úgy valósította meg, hogy a gravitációs alapegyenletébe berakott egy új tagot, amit Λ-val jelölt, és amit kozmológiai állandónak nevezünk.

A fenti egyenlet magyarázatát korábbi írásomban („Einstein igazsága és tévedései”) már megadtam, de a könnyebb olvashatóság kedvéért újra összefoglalom a fontosabb megállapításokat.

A gravitációs egyenlet paraméterei

A tömegek pozíciója és sebessége adja a „forrást” az egyenlet jobb oldalán, amit matematikailag az energia-impulzus tenzor T_ab ír le, ahol az alsó index a görbült téridő koordinátáit jelöli. Ez alapján kell meghatározni a g_ab metrikus tenzort, ami a koordináta szorzatok együtthatója. A speciális relativitáselméletben (Minkowski téridő) g_ab egy négydimenziós diagonális mátrix: (1, -1,-1,-1) sajátértékekkel, ahol az első index az idődimenziónak felel meg. Ha ismerjük a görbült tér  g_ab metrikus tenzorát, akkor ebből parciális deriválások segítségével képezhetjük az R_ab görbületi tenzort, amit Ricci tenzornak nevez az irodalom. A Λg_ab tag nem függ a görbületi tenzortól csak a metrikától és előjele pozitív, ami a taszítást (antigravitációt) jeleníti meg.

A Hubble-féle tágulási törvény

Néhány évvel Einstein publikációjának megjelenése után Hubble a távoli galaxisok vörös eltolódása alapján kimutatta, hogy az Univerzum nem sztatikus, hanem tágul. Einstein azonnal elismerte tévedését és a kozmikus állandó bevezetését élete legnagyobb tévedésének nevezte. Az utókor mégis igazat adott Einsteinnek a kozmológiai állandó létezését illetően, mert a távoli szupernóva robbanások vörös eltolódása arra mutat, hogy az Univerzum gyorsulva tágul, szemben a tisztán gravitációt feltételező modellel, amely lassuló tágulást hozna létre.

Hubble 1929-ben publikált megfigyelésének lényege, hogy minél távolabb van tőlünk egy galaktika, annak távolodási sebessége arányos a d távolsággal: v = H.d, ahol a H állandó értéke a legújabb mérések szerint  H = 73,00±1,75 km/Mpc.s.

Az ősrobbanás elméletének születése

Érdekes módon a Hubble törvény magyarázata két évvel megelőzte a törvény megszületését, amikor Georges Lemaître 1927-ben Einstein általános relativitáselmélete alapján adott magyarázatot a spirális galaxisok távolodására. Felvetette az „ősatom” koncepcióját feltételezve, hogy a galaxisok távolodása az Univerzum alapjelensége, amit visszavetítve a messze múltba, kellett lenni egy olyan kezdő pillanatnak, amikor az összes galaxis egyetlen matematikai pont volt, amelyben az egész Univerzum összes energiája benne foglaltatott. Meghökkentő állítás, ha arra gondolunk, hogy milyen óriási energia van a Napban és a Nap csak egy szerény csillag a Tejútrendszer milliárd csillagja közül, és a galaxisok száma is eléri a milliárdot! Szabad-e ilyen messzire extrapolálni, mi a garancia arra, hogy a fizika törvényei változatlanok ilyen extrém körülmények között, amikor a nyomás, az anyagsűrűség és a hőmérséklet elképesztő mértékben megemelkedik?

Lemaître koncepciója szerint, amikor az „ősatom” szétszakad – később ezt nevezték el ősrobbanásnak – az egyes elemek minden irányban, de különböző sebességgel távolodnak az eredeti pozícióhoz képest. Ha például az egyik sebessége v₁, a másiké v₂, akkor T idő alatt v₁T illetve v₂T az eltávolodás a kezdőponttól és így a közöttük lévő távolság d = (v₂ – v₁)T  arányos lesz a sebességkülönbséggel és a T idő – amit a mai számítások 13,788 milliárd évre becsülnek – a H állandó reciprokának felel meg, legalább is akkor, ha idő közben a sebességek nem változnak meg. Bár az egyes galaxisok távolságát saját magunktól mérjük, ebből nem következik, hogy magunkat tekinthetnénk az Univerzum centrumának, mert a távolodási törvény az Univerzum bármely pontjáról nézve azonos lesz.

Friedmann koncepciója az Univerzum tágulásáról

Alexander Friedmann orosz matematikus és fizikus foglalkozott avval a kérdéssel, hogy a Hubble állandó hogyan változik Einstein gravitációs egyenlete alapján. Az Univerzumot homogén és izotróp folyadéknak képzelte el, amelyben a galaxisok minden irányban és minden távolságban egyforma számban és sűrűségben találhatók meg. Számba vette a gravitáció és a kozmikus taszítási tagon kívül a fénynyomást és a tér görbületét leíró „k” faktor hatását is, ahol az utóbbi a sík euklideszi geometriában nulla, míg a két lehetséges előjelű görbületet +1 és -1 közötti érték írja le. A jelenkori H₀-hoz viszonyítva adta meg a változó H értéket:

A tágulási paraméterek szemléletes értelmezése

A Friedmann egyenletet szemléletesen értelmezhetjük a bevezetőben bemutatott szökési sebességek alapján. A szökési sebesség négyzete függ az M tömeg és a Föld R sugarának arányától. A négyzetes összefüggés itt a H állandóban jelenik meg, az omega együtthatók hozhatók kapcsolatba a sűrűség jellegű mennyiségekkel, és fellép a formulában A, tehát  az Univerzum teljes mérete, hasonlóan ahhoz ahogy a szökési sebességnél a Föld R sugara játszik szerepet.

Értelmezzük először  A hatványait! Az első tag, ami a fénynyomás hatását írja le A^-4-el arányos. Ennek oka, hogy egyrészt a nyomás az Univerzum felületével, vagyis A²-tel arányosan csökken, másrészt a fény intenzitása is csökken a galaxisok távolságának négyzetével. A második tag Ω_m jellemzi az anyagsűrűség gravitációs hatását, itt A^-3 azért lép fel, mert a sűrűség fordítva arányos a térfogattal. A harmadik tag, amelynek Ω_k az együtthatója a tér görbületéből fakadó nyomást írja le és A^-2 fejezi ki, hogy a nyomás fordítottan arányos a felülettel. Végül az Ω_Λ tag nem függ az Univerzum méretétől, mert Einstein egyenlete szerint csak a metrika befolyásolja és nem számít, hogy lokálisan mekkora a tér görbülete. Úgy is felfoghatjuk Ω_Λ-át mint az Univerzum születési energiáját, ami később sem változik meg.

Az Univerzum első korszaka: a fénynyomás uralma

Az Univerzum korszakváltásait kiolvashatjuk a Friedmann formulából!  A kezdetekben, amikor az Univerzum parányi volt, az A^-4 függés miatt a fénynyomás dominált és a tágulási sebesség rendkívül nagy értéket vett fel, ami sok-sok nagyságrenddel haladta meg a fény sebességét. Ezt a szakaszt, ami a számítások szerint a másodperc tört részéig tartott nevezzük az Univerzum inflációjának. De hogyan értelmezhetjük ezt a fénysebesség állandóságának törvényével? Korábbi írásokban már utaltam rá, hogy a maximális kölcsönhatási sebesség a biztosítéka, hogy az Univerzum nem robban fel, hiszen ha nincs felső határ, akkor minden hatásra késletetés nélkül jön a válasz, amelynek végtelenhez tartó összege szétrobbantaná az Univerzumot! De hát a kezdeti szakasz, amely a másodperc töredékéig tartott nem más mint maga a robbanás! A fénynyomás uralkodásának korszakában az Univerzumban nem volt, ami korlátozta volna a fényt.

Volt- az Univerzumnak Planck korszaka?

Az Ősrobbanás elmélete megáll a Planck időnél: 

mert ezelőtt már a kvantummechanikai bizonytalanság miatt elmosódnak a határok, de ha a fénynyomás korszakban a végtelenhez fut a sebesség, akkor ez az idő nulla felé tart. Lehet, hogy emiatt nem is beszélhetünk az Univerzum Planck korszakáról, mert tetszőlegesen rövid ideig haladhatunk az elmélettel az ősrobbanás kezdete felé.

Az Univerzum gravitációs korszaka

 Az Univerzum túlélte ezt a korszakot, ami alatt mérete óriásira nőtt, és lecsökkent a kezdeti hatalmas sűrűség és hőmérséklet, és ennek következtében beindulhatott először az elemi részecskék, majd később az atomok felépülése, kialakulhattak a csillagok és galaxisok is. Erről írtok részletesebben „ Az ősrobbanás és a teremtésmítoszok” című bejegyzésben. Ekkor jött el a második korszak, amikor az anyag gravitációs hatása dominálta már az Univerzumot. Ebben a korszakban már nem a fény volt az úr és sebességét a gravitáció visszafogta és már nem kellett tartani újabb robbanástól. Ez már egy konszolidált Univerzumot hozott létre, ekkor az Univerzum tágulási üteme is lassulni kezdett.

Az Univerzum antigravitációs korszaka

 A jelenlegi kozmológiai elmélet szerint ez a szakasz hét és fél milliárd évig tartott és utána a tágulási sebesség gyorsulni kezdett és ez folytatódik napjainkig is. Ebben a korszakban az antigravitáció már hatásában túlnő a gravitáción, aminek oka, hogy Ω_Λ nem függ az Univerzum méretétől. A sokasodó és egyre pontosabb csillagászati megfigyelések fokozatosan pontosítják az Univerzum tágulásáról szóló ismereteinket. Felmérték, hogy az átlagos sűrűség annak felel meg, hogy 0,2 proton jut minden köbméterre, viszont a megfigyelt tágulási sebességhez ennél sokkal többre lenne szükség, mintegy 5 protonnak megfelelő tömegre. Kell tehát lenni egy olyan anyagnak, ami kibújik a megfigyelések alól, ezt nevezték el sötét anyagnak, ami a teljes tömeg 95 százalékát képviseli. Más számítások az antigravitáció hatását vetették össze a gravitációval és azt kapták, hogy a tér szerkezetéhez kapcsolható antigravitáció – amelynek energiáját „sötétnek” nevezi a szakirodalom – szintén túlsúlyban van és az Univerzum teljes energiájának 69 százalékát teszi ki.

Nem ejtettünk szót a görbületi nyomásról, amely szintén a gravitáció hatása fölé nőhetne az A^-2 függés miatt. Viszont a kis átlagos anyagsűrűség következtében az Univerzum görbülete csak lokálisan lehet nagy a fekete lyukakban, de összességében a tér geometriája közel van a síkhoz és emiatt hatása nem lehet jelentős.

Záró gondolatok

Fizikai világunkat négy különböző erő szabályozza: a gravitáció, az elektromágneses kölcsönhatás és az elemi objektumok erős és gyenge kölcsönhatása. Ezek közül a gravitációnak hármas arca van. Az egyik az elemi részecskék sajátmozgásának stabilitását biztosítja, ez az erős gravitáció. A másik hétköznapi világunkban fejti ki hatását, ez az erő, amely minket a földhöz tapaszt, de ez forrasztja össze az anyagot bolygókká, csillagokká és galaxisokká, és ez szabályozza kölcsönös mozgásukat. De van egy harmadik arca is, amelyik a galaxisok világában fejti ki hatását, távol tartja egymástól őket és nem engedi, hogy egymásba zuhanjanak. Ez gondoskodik az egész Univerzum stabilitásáról és ez jelenik meg Einstein gravitációs egyenletében a kozmikus állandó, azaz a lambda tag képében.

A blog egyéb írásait összegzi és megadja a linkeket a „Paradigmaváltás a fizikában” című bejegyzés

Az állandóság keresése a változásban

Világunk állandó változásban van, de ha meg akarjuk érteni, akkor keresni kell, hogy mi az állandó a változások mögött. Ezt keresi a fizika is, amikor kialakítja a maga saját fogalomrendszerét. Az út fontos állomása a nyugalmi energia. De hát lehet a nyugalom az energia forrása?  Ennek megértéséhez először fussunk végig a mechanika fogalmain a klasszikus felfogástól kezdve a relativitás elvéig.

Az erő mint a változás oka

A világot annak teljes összefüggő rendszerében nem tudjuk leírni, ezért megkülönböztetünk benne elkülönült komponenseket. Mindenekelőtt magunkat elválasztjuk a külvilágtól és a valóságot a kívülről érkező hatások alapján írjuk le. A külső világot felosztjuk fizikai objektumok sokaságára és keressük közöttük a kölcsönhatásokat, amelyeket törvényekbe foglalunk. Feltesszük a kérdést, hogy mi hozza létre a kölcsönhatásokat az objektumok között, amit erőnek nevezünk. Erő, ami a földhöz tapaszt minket, erő, amit a gyorsuló járműben, vagy a körhintában érzünk, de erők kapcsolják össze és alakítják át a legkisebb elemi részecskéktől kezdve egészen a leghatalmasabb objektumokat, a galaxisokat is. Az erő mozgásokat hoz létre, az erő hiánya, vagy különböző erők egymást kiegyenlítő hatása esetén nem változik meg a mozgás jellege. Ebből indult ki Newton is, amikor megfogalmazta a maga  mozgástörvényeit.

Sebesség, gyorsulás, tömeg

Az erő által okozott mozgásváltozást a mechanika vizsgálja. Első lépésben leválasztja a mozgást gátló erőket, a súrlódást és a közegellenállást és az egyenletes sebességű mozgást tekinti a változatlan mozgási állapotnak és az erő hatását azáltal jellemzi, hogy mekkora változás következik be a sebességben, azaz mekkora a gyorsulás. Ugyanaz az erő az egyik tárgyat jobban, a másikat kevésbé gyorsítja fel, ami elvezet a tehetetlenség, a tömeg fogalmához. Így jutunk el Newton második törvényéhez, amelyben a tömeg az erő és a gyorsulás arányát fejezi ki: m = F/a. A tömegre egy fontos szabály érvényes: ha több testet együtt gyorsítunk fel, akkor a tömegek összeadódnak.

Az impulzus a mozgásmennyiség mértéke

A mechanika következő fogalmát a golyók rugalmatlan ütközéséből vezethetjük le. Vízszintes terepen gurítsunk el egy m₁ tömegű golyót v₁ sebességgel. Ha a súrlódástól eltekinthetünk és nem hat rá külső erő, akkor Newton első törvénye szerint a golyó sebessége állandó marad. Ütközzön a golyó egy m₂ tömegű álló golyóba – még pedig rugalmatlanul – ami azt jelenti, hogy az ütközést követően a két golyó összetapad és együtt halad tovább. Mérjük meg az ütközés után a most már m₁+m₂ tömegű golyó sebességét, azt találjuk, hogy a sebesség

lesz, vagyis átírva:  m₁.v₁ = (m₁+m₂)v_új . A kísérletet megismételhetjük úgy is, hogy mindkét golyó mozogjon. Valamennyi ütközésnél azt tapasztaljuk, hogy a golyók összetapadása után akkora lesz a sebesség, ami megfelel az

m₁.v₁ + m₂.v₂ = (m₁+m₂)v_új

szabálynak. Ebből azt a tanulságot vonhatjuk le, hogy ha a tömeg és sebesség szorzatait összeadjuk a két golyó ütközése előtt és utána, akkor az összeg nem változik. Evvel a mozgásmennyiség fontos jellemzőjéhez jutottunk, az impulzushoz, amit a mozgó golyók tömegének és sebességének szorzata fejez ki: p = m.v.

Az impulzus fogalmára általánosabb definíciót is adhatunk, amelynek érvényessége tetszőleges ütközésre, így a rugalmas ütközésre is érvényes: az impulzus olyan fizikai mennyiség, amely megmarad amikor nem hat a vizsgált objektumra külső erő.

A rugalmas ütközés megmaradási szabályai

Most térjünk át a rugalmas ütközések esetére, amikor az v₁ és v₂ sebességgel ütköző golyók nem sérülnek és az ütközést követően valamilyen v’₁ és v’₂ sebességgel haladnak tovább. Használjuk fel az impulzusmegmaradás törvényét, mely szerint

m₁.v₁ + m₂.v₂ = m₁.v’₁ + m₂.v’₂                                                     (1)

A rugalmatlan ütközés esetétől eltérően, ahol az impulzusmegmaradás törvénye elég volt, hogy meghatározzuk az összetapadt golyók sebességet, most ez nem lehetséges, mert két független sebességet kell meghatározni. A klasszikus fizika alapelve, ha egy kísérletet azonos körülmények között megismétlünk, akkor az eredménynek azonosnak kell lenni. Ez azt jelenti, hogy létezik valamilyen további törvényszerűség, amely pontosan meghatározza, hogy mekkora lesz az ütközés után a két golyó sebessége külön-külön. Különböző tömegű és sebességű golyók esetén elvégezve az ütközéses kísérletet, azt fogjuk tapasztalni, hogy létezik egy második megmaradási törvény is, amely kimondja, hogy ha a tömeget a sebesség négyzetével szorozzuk, akkor ezek összege az ütközés során nem változik:

Ez a második megmaradási törvény vezet el a mozgási energia fogalmához, amely az impulzusmegmaradási törvénnyel együtt egyértelmű leírást ad a rugalmas ütközés kimenetelére. A kissebességű folyamatokban, ahol nem relativisztikus közelítést alkalmazunk, a mozgási energia kifejezésében fellép az ½ faktor is.

Energiamegmaradás és a hőenergia

Ha nem hat a golyókra külső erő és az ütközés tökéletesen rugalmas, akkor a mozgási energia megmarad. A rugalmatlan ütközésben azonban a mozgási energia jelentős részben elvész. Az energiamegmaradás törvénye ilyenkor azt jelenti, hogy a mechanikai energia részben rendezetlen mozgássá, azaz, hőenergiává alakul át, ami azonban nem jár impulzusveszteséggel. Az impulzus azért nem változik meg, mert a rendezetlen mozgásban a golyót alkotó részecskék (molekulák) minden irányban egyforma valószínűséggel mozognak és hatásuk átlagban nulla lesz. Evvel szemben az egyes részecskék mozgási energiája a sebesség négyzetével arányos, amely nem függ az iránytól és csak pozitív lehet. Az egyes részecskék mozgási energiájának összegét nevezzük hőenergiának.

Az erő és az impulzusváltozás

Ha valamilyen erő hat a testre, akkor annak mozgási sebessége megváltozik, amit az impulzusváltozással, vagy pontosabban szólva az idő szerinti differenciálhányadossal jellemezhetünk: F = dp/dt. Nem relativisztikus esetben ez a már említett F = m.a erőtörvénynek felel meg – de szemben az erő és gyorsulás kapcsolatát megadó törvénnyel – az erő és impulzusváltozás arányossága a relativisztikus mechanikában is fennáll.

A fizikai munka és a potenciális energia

Az erőhatását leíró potenciális energia fogalmához a fizikai munkavégzés segítségével jutunk el. Ha felemelünk egy testet, akkor a gravitációs erővel szemben végzünk munkát és ezáltal a test potenciális energiáját növeljük meg. Ha elengedjük a testet, akkor gyorsuló mozgással leesik, azaz mozgási energiára tesz szert a potenciális energiacsökkenés révén. A gravitációs erőt az F = - m.g adja meg (g a földi gravitációs gyorsulás), ahol a negatív előjel fejezi ki, hogy az erő iránya lefelé mutat. Ha z magasságba emeljük fel a tárgyat, akkor m.g.z munkát végzünk, tehát ez lesz a potenciális energia. A potenciális energiát a z változóval deriválva d(m.g.z)/dz = m.g értéket kapunk, ami az erő kifejezése fordított előjellel. Ezt fejezi ki az a megfogalmazás, hogy az erő a potenciális energia negatív deriváltja. (Általános esetben vektorokat kell alkalmazni az erő irányának jellemzésére, amelyet a potenciális energia negatív gradiense határoz meg). A test mozgása során, ha a potenciális energia és a mozgási energia összegét képezzük (itt a (2) egyenletben az ½ faktor fog szerepelni), akkor az erőtörvény alapján kimutatható, hogy a mozgás során ez az összeg állandó marad. Az energiát tehát két tagból építjük fel: az egyik felel meg az erő sebességváltoztatási képességének, ez a potenciális energia, a másik pedig a már létrehozott mozgást jellemzi, ez a mozgási, vagy kinetikus energia.

Változik-e a tárgyak hossza, ha mozognak?

A hétköznapi tapasztalataink alapján megalkotjuk a tér fogalmát, amelyben elrendezzük a tárgyak egymáshoz képesti helyzetét, míg az idő segítségével rakjuk sorba az eseményeket és különböztetjük meg az okot és az okozatot. Köznapi gondolkozásunkban nem merül fel a gyanú, hogy más képet kellene alkotunk a környező világról, amikor benne vagyunk, vagy amikor mozgás közben szemléljük. Ennek szemléltetésére képzeljük el, hogy egy v sebességű vonaton utazunk és az ablakból kinézve akarjuk meghatározni két pózna távolságát. Tegyük fel, hogy pontosan ismerjük a sebességet és mérjük a Δt idő különbségét, amikor elhaladunk két pózna mellett, ekkor a távolság Δs’ = v. Δt. Fel se merül bennünk a kétség, hogy ez a távolság más lenne, ha egy mérőrúddal kint határoznánk meg a póznák Δs távolságát. Pedig a relativitáselmélet pont ezt mondja ki, amikor bevezeti a Lorentz kontrakció fogalmát, mely szerint:

A formula reciproka  adja meg a Lorentz kontrakció mértékét, ami akkor válik jelentőssé, ha a v sebesség értéke közel van a c fénysebességhez. Emiatt van, hogy a megszokott körülmények között elhanyagolhatjuk a redukciót, hiszen, még az űrhajók sebességén is rendkívül csekély a rövidülés:

1/ β = 0,999 999 995

A Galilei és a Lorentz transzformáció

Ha a póznák távolsága 1 méter, akkor méterrudunk hossza látszólag megrövidül. Mérjük meg a pozíciónkat és a megtett utat evvel a rövidebb méterrúddal, ekkor számszerűleg nagyobb értékeket kapunk. Nem-relativisztikus közelítésben, ha s méri a kezdeti pozíciónkat és t idő telik el, akkor a kezdeti, már hátrahagyott helyzetnek megfelelő pozíciót a vonatból az s’ = s — v.t összefüggés határozza meg. Ezt szokás Galilei transzformációnak is nevezni. Relativisztikus esetben a rövidebb méterrúd miatt ez β szorosára növekszik:

s’ = β(s — v.t)                                                               (4)

Ami még szokatlanabb, hogy óránk is más ütemben ketyeg a nagysebességű vonaton, sőt a mért idő még attól is függ, hogy hol volt a kezdeti pozíciónk:

t’ = β(t — v.s/c²)                                                              (5)

A (4) és (5) összefüggéseket nevezzük Lorentz transzformációnak. A Galilei transzformációban természetesen t’ = t. A (4) és (5) transzformációkban a tér és idő tehát kölcsönösen függ egymástól, míg a Galilei transzformációban a kapcsolat aszimmetrikus. Minkowski azért vezette be a téridő fogalmát, hogy a tér és idő dimenziók elválaszthatatlan kapcsolatát hangsúlyozza a mozgások leírásában. Érdemes rámutatni, hogy az elektrodinamika alapegyenletei, a Maxwell egyenletek már eleve a Lorentz transzformáció szabályának engedelmeskednek. Ennek oka, hogy ezek az egyenletek már a fény terjedési szabályait is leírják, már pedig a fény terjedése igazán relativisztikus, hiszen épp innen származik a  c sebesség.

Az idő dilatáció szemléletesebb összefüggéséhez juthatunk (5)-ből, ha az s = v.t összefüggés alapján átalakítjuk a transzformációs formulát:

t’ = βt(1 – v²/c²) = t/β                                                                   (6)

Innen láthatjuk, hogy az idő dilatáció mértéke voltaképp megegyezik a hosszúság (3) szerinti Lorentz kontrakciójával.

Mit értünk kovariáns alatt a relativitáselméletben?

             Alkalmazzuk a (4) és (5) Lorentz transzformációt, hogy felépítsünk egy speciális mennyiséget, amely független lesz attól, hogy mekkora a választott inercia rendszer v sebessége, amelyben a méréseket végezzük.(inercia rendszerről beszélünk, ha a sebesség nem változik): Ez a mennyiség:

c²t² – s² = c²t’² – s’²                                                                   (7)

Ezt a kifejezést nevezik a relativitáselméletben kovariánsnak. Einstein mutatta ki, hogy ez a kovariancia a fénysebesség állandóságából következik, azaz bármekkora és bármilyen irányú inercia rendszerből is származik a fénysugár, annak sebessége vákuumban mindig pontosan ugyanakkora. Ebből következik, hogy a fénysebesség nem fokozható azáltal, ha mozgó objektumból bocsátjuk ki. Ez is meglepő állítás, pedig valójában természetesen következik az univerzum létezéséből. Ha a kölcsönhatások sebességének nem volna felső határa, akkor a hatásokra érkező viszontválaszok végtelen sokasága egy időben jelentkezne, ami vagy felrobbantaná, vagy megszüntetné az univerzumot.

Az energia és impulzus kapcsolata a relativitáselméletben

A relativitáselmélet másik alapvető kovariánsa az energiából és az impulzusból épül fel:

E² – p²c² = állandó = E₀²                                                                  (8)

Az inercia rendszer választása egyaránt megváltoztatja az energiát és az impulzust, hisz mindkét mennyiség az objektum sebességétől függ, de a négyzetek különbsége mégis állandó marad. Ha a kvantummechanikai operátorok definíciójából indulunk ki, amely szerint az energia a t időszerinti, az impulzus az s hosszúság szerinti differenciállal arányos, akkor a (8)-ban megadott kovariáns tulajdonképpen a (7) kovariáns differenciális alakja. A (8) egyenletben szereplő állandó képezi az objektum nyugalmi energiáját.

A tömeg sebességfüggése

A relativitáselmélet legfőbb megállapítása, hogy az energia és a tömeg fogalma összekapcsolódik a nevezetes E = m,c² összefüggés szerint. Ez kapcsolja össze a nyugalmi energiát és az m₀  nyugalmi tömeget: E₀ = m₀c², és helyettesítsük be (8) egyenletbe az impulzus p = m.v alakját, ami által eljutunk a tömeg sebességfüggési törvényéhez:

m²c² – m²v² = m₀²c⁴, azaz  m² = m₀²c²/(1 – v²/c²) =   β²m₀²                               (9)

A tömeg sebességtől való függése miatt a golyók rugalmas ütközésénél bevezetett és a mozgási energiához vezető (2) egyenlőség csak közelítőleg érvényes. Az energia-impulzus kovariáns alapján az energia kifejezése:

Kis sebességeknél eltekinthetünk a tömeg sebességfüggésétől és felírhatjuk a négyzetgyök Taylor sorát

:

A nem-relativisztikus energiában innen származik az ½-es faktor, a következő tag pedig a relativisztikus korrekció.

További következménye a tömeg sebességfüggésének, hogy a newtoni F = m.a egyenletnél általánosabb az erő és az impulzus differenciálhányadosa közötti összefüggés, hiszen ekkor a tömeg idő szerinti differenciálását is figyelembe kell venni.

Honnan származik a nyugalmi energia?

Most már rátérhetünk a címben felvetett kérdésre, hogy mi is a nyugalmi tömeg és nyugalmi energia forrása? A fizikában az energiaformák egymásba alakulásáról beszélünk, a potenciális energia átalakul a mozgási energiává, a mozgási energia hőenergiává alakulhat át és még sorolhatnánk. Minden esetben a mozgás a kulcsszó, de mit kezdjünk a nyugalmi energiával, amikor az energia nem más mint a mozgás legfőbb megjelenési formája? Már ez a logika is arra ösztönöz minket, hogy a „nyugalmi” energia mögött is valamilyen mozgást keressünk! Mégpedig nem akármilyen mozgást, hiszen óriási energiáról van szó!.

 Amikor kémiai reakciókban energia szabadul fel, akkor megfigyelhető, hogy a képződő vegyületek össztömege egy milliárdod résszel kisebb, mint  amiből létrejött, amikor egy nehéz radioaktív atom szétbomlik, akkor a töredék atommagok tömegösszege ezrednyivel kisebb, mint a széteső atom, ami hatalmas energia kibocsátást eredményez, még több energia szabadul fel, amikor a legkönnyebb atomok hélium atommagot hoznak létre a fúzió során, mert ilyenkor már 1 százalék körül van a tömegdeficit, de a legnagyobb tömegvesztés az anyag-antianyag annihilációban jön létre, amikor a teljes tömeg eltűnik. A tömegdeficit minden esetben a képződő mozgási és hőenergia forrása. Ebben az értelemben a tömeget, mint potenciális energiát tekinthetnénk, de zavaró, hogy az energia formulákban mindig a potenciális energia lineárisan összegződik a többi taggal, míg a (8) összefüggés szerint négyzetes összegzési szabály érvényesül. Már ez is arra utal, hogy ne potenciális energiaként tekintsünk a nyugalmi energiára, hanem mozgási energiaként.

A fénysebesség szerepe a nyugalmi energia kialakulásában

Ha az elemi részecskék tömegét mozgásként akarjuk értelmezni, csak a fénysebesség jöhet szóba. Miért? Azért mert ez az egyetlen abszolút sebesség, minden más sebesség attól függ, hogy milyen inercia rendszerből nézzük. A fénysebesség viszont a téridő alapsebessége. Evvel rendelkezik a foton is. A fénysebességű mozgás a relativitáselmélet szerint szingularitást jelent, mert ekkor a β tényező végtelen lesz. Emiatt bármely nyugalmi tömeg végtelen lenne a (9) összefüggés szerint. A fotonnak ezért nincs is nyugalmi tömege, de van energiája a h.ν szabály szerint (h a Planck állandó és ν a frekvencia), de hát akkor mégis van tömege, ha az E = m.c² törvény minden fizikai objektumra, így a fotonra is érvényes. Az egyetlen lehetőség az ellentmondás feloldására, ha azt tételezzük fel, hogy a végtelenbe futó β a fénysebességű mozgásokban egy határértékben nulla értékkel szorzódik, ami által a szorzat véges értékű lesz, mint ahogy β*1/β = 1, akkor is, ha β határértékben végtelen! De mi lehet ez a határértékben nulla tömegű objektum, ami tömegre tesz szert a fénysebességű mozgás által? Van valami rejtélyes eredetileg nulla tömegű anyag a térben, amely fénysebességű mozgásba lendül?

A tér és idő fogalmaink kialakulása

De hogyan is alakult ki fogalmi rendszerünk a térről és az időről? Szemünkbe minden pillanatban óriási mennyiségű foton érkezik, amit szemlencsénk a retina különböző pontjaira vetít. Ez az információ az idegpályákon az agyba jut, ott feldolgozásra kerül, majd kialakul a kép, amely összegzi az optika szabályain alapulva, hogy honnan is érkeztek az egyes fotonok. Az így létrejött térképzet kiegészül egyéb érzékszerveink által nyert információval is. De ez a tér sztatikus, olyan, mint egy tartály, amelyben elrendezzük a tárgyak helyét és mozgását, és erre a térképzetre épül a részecskefizika is, amikor az anyag legkisebb objektumainak tulajdonságait vizsgálja. Térképzetünk jelentősen tovább fejlődött a nagysebességű mozgások értelmezésére létrejött relativitáselmélet által, ezáltal jutottunk el a téridő fogalmához, amelyben a tér, az idő és a mozgás már elválaszthatatlan egységet alkot, de még ez a kép is úgy kezeli a részecskéket, mint amelyek „benne vannak” a térben.

A dinamikus tér fogalma

Az előbbiekben felvetettem a kérdést, hogy mi azaz „anyag”, amiből a fénysebességű mozgás létrehozza a részecskéket. A választ a tér fogalmának kiterjesztésében keresem, amely nem puszta „tartály”, hanem maga is dinamikus fogalom, amely lokálisan fénysebességű saját mozgásokat végez. Ennek a térnek immanens tulajdonsága, hogy a fénysebességű mozgások által tömegre, energiára, impulzusra, impulzusnyomatékra (spinre) és töltésekre tesz szert. Több korábbi írásban („Az elemi részecskék mozgásformái”, „ A tér szerkezete és az elemi részecskék mint rezonanciák”, „ Téridő-részecske”, Fénysebességű forgások és a relativitáselmélet„”) már ismertettem ezt a modellt, amit fénysebességű forgásmodellnek hívok. Különböző módon kapcsolódhat össze két mozgásforma: a forgás és a haladás, és ez határozza meg, hogy fotonokról, illetve egyéb kölcsönhatást közvetítő bozonokról beszélünk, vagy fermionokról, mint az elektron, pozitron, neutrínó, vagy akár a kvarkok. Tehát nem arról van szó, hogy vannak térben mozgó részecskék, hanem arról, hogy a tér maga sajátforgásai által hozza létre a részecskéket. Ez a sajátforgás lesz a nyugalmi tömeg forrása is. Tehát a nyugalmi tömeg éppen hogy nem a nyugalomban lévő részecske tartozéka, hanem a fizikailag létező lehető leggyorsabb forgás! Amikor tömegdeficit jön létre, vagy a tömeg teljesen eltűnik, akkor ez az óriási sebességű forgás lesz a forrása az átalakulások során képződő sugárzási és mozgási energiának.

:

A korábbi bejegyzések összefoglalását és a megfelelő linkeket lásd: „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”.

A Proxima b Centauri Földhöz hasonló tulajdonságai

Nagy port kavart fel a tudományos felfedezés, hogy a hozzánk legközelebbi csillagrendszer egyik csillaga, a Proxima Centauri körül kering egy föld-típusú kőzetbolygó, ami a Proxima b elnevezést kapta. Az izgalomra az adott okot, hogy ez a bolygó olyan távolságban kering a napjától, hogy az onnan érkező sugárzás valószínűleg olyan hőmérsékletet hozhat létre a bolygó felszínén, ami közel lehet a földi viszonyokhoz. Ez a távolság ugyan húszszor kisebb, mint a Föld-Nap távolság, de ez a nap a vörös törpék családjába tartozik, amiért az onnan érkező sugárzás intenzitása sokkal gyengébb, mint a mi napunké. Természetesen még nagyon keveset tudunk erről a bolygóról, nem tudjuk, hogy van-e légköre, vannak-e tengerei, ami alapvető az életfeltételekhez. Ami a felszíni gravitációt illeti, az közel lehet a Földön megszokotthoz, mert a bolygó tömege 1,3-szorosa a Földhöz képest és ha kőzetbolygóról van szó, akkor a sugara is közel lehet a mi bolygónkhoz. Annyit tudunk még, hogy ott egy év nagyon rövid, mert 11,2 nap alatt keringi körül saját csillagát, forgásáról, azaz napjai hosszáról még nem tudunk semmit. Központi csillagának tömegét tudjuk a Newton-Kepler törvény alapján, mely szerint ez a tömeg R³/T²-el arányos, ahol az előbbi a keringési sugár, a másik a keringési idő. Számításba véve, hogy az előbbi 20-szor, az utóbbi 32,6-szor rövidebb, mint a Földé, azt kapjuk, hogy a Proxima Centauri tömege a Nap 13,3 százaléka.

Milyen sugárzás éri a Proxima b Centauri felszínét?

Az élet lehetősége szempontjából fontos a bolygóra érkező sugárzás összetétele. Vörös törpéről van szó, azaz a csillag felszíni hőmérséklete jóval alacsonyabb, mint a Napé, és a fekete test sugárzás törvényéből tudjuk, hogy ekkor a látható, az UV és a még nagyobb frekvenciájú sugárzás részaránya jóval kisebb a vöröshöz képest. Ez annyiból jó, hogy a csillaghoz való kis távolság ellenére az ártalmas sugárzásmennyisége is kisebb lehet, de problémát jelenthet a látható tartományba kevesebb fény jut. A Föld történetéből tudjuk, hogy oxigénben gazdag légkörünket a növények, algák, egysejtűek fotoszintézisének köszönhetjük. Kérdés, hogy ha ez a sugárzási tartomány nem elég intenzív, akkor megvalósulhatott-e a fotoszintézis és így számíthatunk-e oxigénben dús légkörre.

Mennyi üzemanyag kell, hogy elérjük a Proxima b Centaurit űrhajóval?

De legyünk optimisták és induljunk ki abból, hogy megvannak az élet feltételei ezen a ’második Földön’. Ekkor érdemes újragondolni, hogy van-e lehetőségünk arra, hogy eljussunk oda. A sci-fik világában ez nem okoz problémát, az űrhajók vígan röpködnek a csillagok között, csak hát ekkor nem veszik számításba, hogy mennyi és milyen üzemanyag szükséges ezekhez az űrutazásokhoz. Korábbi bejegyzésben („Hogyan látogathatjuk meg a legközelebbi csillagokat”) már végeztem egy becslést, hogy mennyi üzemanyag kellene, hogy megtegyünk az Alfa Centaurira egy körutat. Az volt a konklúzió, hogy a szükséges üzemanyag mennyisége, még antianyag reaktor esetén is rendkívül nagy nem beszélve a kockázatokról. Kicsit jobb a helyzet, ha megelégszünk az oda úttal és nem kell magunkkal vinni üzemanyagot a visszatéréshez is. Ez messze nem felezését jelenti a szükséges üzemanyagnak, mert a megteendő út függvényében exponenciális a növekedés.

Az űrutazás élettani feltételei

A számítás kiindulópontja, hogy az élettani feltételek miatt a hosszan tartó és a földi gravitációt nagymértékben meghaladó gyorsulás nem viselhető el. Másrészt a célba érkezéskor az űrhajót le kell lassítani, mert egyébként vagy óriási sebességgel becsapódna a bolygó felszínébe, vagy elrohanna mellette. Ezért a rakétatechnika, vagy lézersugaras indítás nem alkalmazható. Élettani szempontból az ’1 g’ gyorsulás az optimális, mert ekkor a földihez hasonló gravitációt érezhetünk. Lehetséges a gyorsuló szakaszok váltogatása egyenletes sebességű szakaszokkal. Az utóbbi szakaszban az űrhajó legénysége súlytalansági állapotban utazik. Ennek időtartamát azonban korlátozni kell, mert hosszabb idő után a csontok és az izmok leépülése már komoly problémát idéz elő.

Váltakozó gyorsulási szakaszok az űrutazásban

Nézzünk meg egy olyan esetet, amikor az idő felét teszi ki az egyenletes sebességű, tehát súlytalansági szakasz. Itt fontos tisztázni, hogy mit értünk az utazási idő alatt, mert ez jelentősen eltér, ha a földi, indulási rendszert, vagy az űrhajóban eltöltött időt vesszük alapul, amikor a sebesség erősen megközelíti a fénysebességet és jelentős az idő dilatációja. Példánkban a földi időből induljunk ki, a teljes t időt három szakaszra bontjuk, az első a gyorsuló t₁ szakasz, a második a súlytalansági t₂, a harmadik a lassulási szakasz: t₃. A t₁ és t₃ szakasz hossza megegyezik, mert nem jelentős a Proxima Centauri sebessége a Naphoz mérten, míg legyen t₂ = 2t₁.

A relativisztikus sebesség változása állandó gyorsulás mellett

A nem-relativisztikus mechanikában állandó g gyorsulás esetén a sebesség arányosan növekszik az idővel: v = g.t. Ez azt jelentené, hogy egy év után már átlépnénk a c fénysebességet, ezért csak a relativisztikus effektusok figyelembevételével kaphatunk reális eredményt. Induljunk ki a relativisztikus sebesség formulájából, amely szerint

A sebességet viszonyítsuk a c fénysebességhez, ami egyszerűsíti a számítást, ha az időt c/g egységben adjuk meg. Mivel c = 3.10⁸m/s és g = 9,81 m/s², így c/g = 3,058.10⁷ s = 0,968 év. Meglepő véletlen, hogy ez az időegység milyen közel van a Föld keringési idejéhez, az évhez, az eltérés csupán 3,3%. Az idő egységének ez a választása annak felel meg, hogy az idő helyett áttérünk az x = g.t/c változóra, amikor is a sebességi formula:

Hosszú idő esetén, azaz ha x >> 1, akkor a v sebesség a c határértékhez tart, amit nem léphet át, megfelelően a relativitáselmélet alapvetésének.

A megtett út relativisztikus számítása

A nem-relativisztikus mechanikában az állandó gyorsulás mellett megtett út s = 1/2g.t², vagy ezt átrendezve t² = 2s/g. Ha a relativisztikus sebességi formulát alkalmazzuk, akkor fellép egy új tag a kifejezésben, azaz t² = 2s/g + s²/c². Az új tag az s = c.t fény által megtett útnak felel meg. Fejezzük ki az s utat az idő függvényében, ami a másodfokú egyenlet megoldásával adható meg és térjünk át az idő esetén a c/g, míg az út esetén a c²/g egységre, azaz az út helyett az y = s.g/c² változót vezetjük be. Az így definiált egységnyi út közel azonos a fényévvel, annál csak 3,3%-kal kisebb. Ebben az egységrendszerben az állandó gyorsulás által megtett út:

A teljes utat, amit a földi koordinátarendszerben határozunk meg, három részre bontjuk, y₁ a gyorsuló, y₂ az egyenletes és y₃ a lassuló szakasz hossza. A lassuló szakasz y₃ hossza megegyezik y₁-el, míg y₂ értékét a relativisztikus sebességformulából adjuk meg (Itt ne feledjük, hogy y₂ is a földi rendszerben érvényes távolság!):

Itt a kettes faktor azért lép fel, mert t₂ =2t₁.

Az utazási idő kiszámítása

Mennyi lesz azaz idő, ami alatt az űrhajó megérkezik céljához, ha a fenti az időmegosztást választjuk? A Proxima Centauri távolsága 4,24 fényév, ami a c²/g egységekben 4,38-nak felel meg. A következő ábra mutatja az út/idő diagramot:

1. ábra. Az űrhajó által megtett út c²/g egységekben, ahol az idő c/g egységben van megadva, a metszéspont mutatja az érkezés idejét.

Az utazás teljes ideje földi években számolva 6,08 lesz, tehát kissé több mint hat év. Az űrhajósok azonban ennél kevesebb időt mérnek óráikon. Az idő dilatációt külön-külön figyelembe véve a három szakaszon, azt kapjuk, hogy a gyorsuló és a lassuló szakaszok ideje 1,52 évről 1,19-ra csökken, míg az egyenletes szakaszon az idő rövidülése 3,04-ről 1,64 lesz és a teljes út 6,08-ról 4,02 évre csökken, tehát rövidebb lesz, mint azaz idő, ami alatt a fény a csillagról a Földre érkezik. Ennek oka, hogy itt különböző rendszerekben mért időket hasonlítunk össze.

Az űrhajó sebességének változása az utazás során

Nézzük meg, hogyan változik az űrhajó sebessége az utazás során:

2. ábra. Az űrhajó sebességének változása a fénysebességhez viszonyítva. Az idő c/g egységben szerepel.

Megváltozott csillagképek az űrhajóban

Az ábrából látható, hogy az űrhajó sebessége jelentősen megközelíti a fénysebességet, ami jelentős mértékű relativisztikus effektushoz vezet. Nézzünk ki az űrhajó ablakából, amikor az egyenletes szakaszban vagyunk és egy megváltozott csillagképet fogunk látni. A változás nem onnan származik, hogy megteszünk egy-két fényévnyi utat, hiszen ez a távolság nagyon kicsi a Tejút 100 000 fényévnyi méretéhez képest, az eltérő csillagkép a nagy sebesség miatt van.. Csillagászaink meghatározhatják, hogy mennyire távolodtunk el Napunktól és milyen messze van még a Proxima Centauri. Ebből megállapítják, hogy a Nap-Kentauri távolság nem 4,24 fényév, hanem csupán 2,28. Jelentősen megváltozik a Nap színe is, az otthon megszokott sárga szín helyett a vörös felé tolódik el, ugyanakkor a Proxima Centauri már nem vörös, hanem a szín elcsúszik a kék felé. Ezek a változások a fény relativisztikus Doppler effektusának felelnek meg. Ha viszont nem előre, vagy hátra nézünk, hanem oldalt, akkor ugyanolyan csillagkép tárul fel előttünk, amit a Földön már megszoktunk.

A megtett út a Földről és az űrhajóból nézve

Hasonlítsuk össze az út három szakaszában a megtett utat, egyrészt a földi rendszerben, másrészt az űrhajóból nézve:

3. ábra. Az űrhajó által megtett út a földi rendszerhez képest (piros) és az űrhajóból nézve (fekete), az idő c/g, az út c²/g egységekben van megadva, a függőleges szaggatott vonalak mutatják a szakaszhatárokat

Az űrhajóban mért út a Lorentz kontrakció miatt rövidül meg, az első és harmadik szakaszban ez a 0,833 fényévet 0,604-re, a másodikban 2,564-et 1,377-re, a teljes 4,24 utat 2,68 fényévre csökkenti le.

Mennyi üzemanyag kell a csillagközi úthoz?

Annak az üzemanyagnak a mennyiségét becsüljük meg, ami a gyorsítási munkához kell. Jelöljük M₀-al a kilövéskor az üzemanyag mennyiségét és m legyen az űrhajó hasznos tömege. A gyorsítási és lassítási szakaszban az M +m tömeget kell g-vel gyorsítani, ahol a kezdeti M₀-ról csökken le az üzemanyag tömege nullára. Példánkban a megtett utat a gyorsítási és lassítási szakaszok teljes hosszában kell biztosítani. Ennek hossza a Lorentz kontrakcióval csökken, mert az űrhajó rendszerében kell figyelembe venni a távolságot, tehát az út 1,2 04 fényév lesz, ami a c²/g egységben 1,244.  A gyorsítási munka azonban fokozatosan csökken, ahogy fogy az üzemanyag. Végezzünk egy közelítő számítást arra az esetre, amikor az üzemanyag mennyisége jóval több, mint az űrhajó hasznos tömege. Ekkor az üzemanyag hosszegységre jutó fogyása arányos lesz magával az üzemanyag mennyiségével: dM/ds = -k.M. Ekkor az üzemanyag mennyisége az út során exponenciálisan csökken: M = M₀.e^-k.s. A tényleges fogyás ennél gyorsabb, mert valójában az M + m teljes tömeget kell gyorsítani, ezért becslésünknél még nagyobb mennyiségű üzemanyagra lesz szükség. A lassítási szakasz végén az űrhajó nem tartalmaz üzemanyagot és így a teljes tömeg lecsökken m-re. Tehát megérkezéskor m = M₀.e^-k.s . azaz

M₀/m = e^k.s

Az összefüggés mutatja, hogy a megtett út hosszától exponenciálisan függ a szükséges hajtóanyag mennyisége.

 Az M tömegű üzemanyagból nyerhető maximális energia a nyugalmi energiával egyezik meg, ami M.c², ennél csak kisebb lehet a ténylegesen kinyert energia, aminek hatásfokát jellemezzük η-val: ηMc².  Az egységnyi úthossz alatt nyert kηMc²energia hozza létre az M.g gyorsítási munkát, ezért

k = g/ηc². Ily módon alsó becslést kapunk az üzemanyag arányára a hasznos tömeghez képest:

Az üzemanyag hatékonyság szerepe az űrutazásban

Ha bármilyen kémiai üzemanyagot használunk a hatásfok kisebb mint egymilliárd, nukleáris bomláskor felszabaduló energiát használva sem érhetünk el egy tízezrednél nagyobb hatásfokot, még fúziós reakciókat felhasználva sem remélhetünk többet 1 százaléknál. Esetünkben y = 1,244 ezért még fúziós reaktor esetén is beláthatatlanul nagy mennyiségű üzemanyagra lenne szükség.

A leghatékonyabb energiatermelés antirészecske reaktorral

Tehát az expedíció alapkövetelménye, hogy az egységhez közel legyen az energiafelhasználás hatásfoka. Lehetséges-ez? Elvben igen, ha az anyag-antianyag annihiláció lenne az energiaforrás, mindenekelőtt az antiproton és a protonok annihilációja lehetne az alap. A probléma természetesen az antiprotonok összegyűjtése és tárolása lenne, mert olyan tartályra lenne szükség, ahol az antirészecske nem érintkezhetne a tartály anyagával. Az antiproton töltött részecske, ezért mágneses térben körpályára kényszeríthető, emellett ha negatív töltésű lenne a tartály, akkor ez eltaszíthatná magától az antiprotonokat. Tehát elvben létrehozható ilyen elektromágneses csapda, de persze ehhez is energia kell, ami a működést biztosítja.

Az antirészecske reaktor kockázatai

Az antiprotonokat a kozmikus sugárzásból lehetne nyerni, mert annak energiája elég, hogy létrejöjjenek ezek a részecskék, de ha ezek a részecskék nagy tömegben vannak összegyűjtve, akkor a kockázat óriásira nő. Akkora mennyiség kellene, ami sokszorosan meghaladja a földön jelenleg tárolt hidrogénbombák nukleáris töltetének teljes tömegét és egy esetleges robbanás hatásfoka ennek több mint százszorosa lenne. Elég egy apró technikai hiba, és ha létrejön a robbanás az nem csak a földi életet pusztítaná el, hanem szétrobbantaná a föld kérgét is. Még nagyobb veszély fenyegetné az űrhajósokat, mert a fénysebesség közelében már nem lehetne előrelátni, ha valamilyen nagyobb űrobjektum kerülne a pálya közelébe, és a manőverezés is nehéz ekkora sebességnél. Így aligha lehetne olyan biztonsági rendszert kifejleszteni, amely elegendő mértékben csökkentené az ütközés és emiatt a robbanás kockázatát.

Drónok küldése a Proxima b Centaurihoz

Az elmondottak miatt bármilyen magas szintre emelkedjen a technika, a csillagközi expedíciónak rendkívül nagy lenne a kockázata. Járható út lehet azonban az automatikus űreszközök, drónok küldése, amelyeket földről irányított energiaforrások (lézerek) segítségével fel lehet annyira gyorsítani, hogy reális idő alatt elérjék a szomszédos csillagokat és onnan küldjenek számunkra híradást a Proxima b Centauri világáról. A második Földnek elnevezett bolygóra történő utazásra ezért nem látok reális esélyt, ez megmarad mindörökre a fikciók világában.

A korábbi bejegyzések összefoglalását és a megfelelő linkeket lásd: „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”.

Mi az anyag alapvető természete: hullámok vagy részecskék alkotják, vagy egyszerre rendelkezik két látszólag ellentétes tulajdonsággal? Ez a fizika talán legfontosabb és sokáig vitatott kérdése. Simonyi Károly (1916-2001) kitűnő monográfiájában „A fizika kultúrtörténetére” című könyvében foglalja össze a fény hullám, illetve részecske elméletének történetét és ismerteti a végső konklúziót, amit egyrészt a relativitáselmélet, másrészt a kvantummechanika ad meg. Ennek ellenére még ma is találkozhatunk ezt vitató nézetekkel, ezért érdemes ezt a kérdést újra áttekinteni és kiegészíteni a foton mellett a többi részecske kettős természetére vonatkozó ismeretekkel.

Newton és kora

A fény kettős természetének vizsgálata Newtonig (Isaac Newton, 1642-1726) nyúlik vissza, aki nem csak saját korának, hanem az egész fizikának egyik legjelentősebb alkotója volt. A mechanika mozgásegyenletei és a gravitációs törvény megalkotása mellett az optika törvényeit is jelentősen tovább lendítette. Nála még a fizikai különböző jelenségeinek vizsgálata együtt járt a matematikai és filozófiai kérdések tárgyalásával, ami megmutatkozik 1687-ben megjelent főművének címében is : „Principia mathematica philosophiae naturalist”. A tudományt annak egységében látta, erre példa, hogy az optikai törvényeinek – például a fény diffrakciójának – felismerése olyan optikai teleszkóp megalkotásához vezette, amely aztán a csillagászat legfontosabb vizsgálati eszközévé vált.

Newton optikai képének megértéséhez tudni kell, hogy még jóval az elektrodinamika törvényeinek, a Maxwell egyenletek megalkotása (James Clerk Maxwell, 1831-1879) előtt vagyunk, nem is beszélve Planck (Max Planck, 1858-1947) 200 évvel későbbi felismeréséről, amikor a fekete test sugárzás magyarázatához bevezette a foton fogalmát. Logikájának megértéséhez azt is tudni kell, hogy abban az időben még nem vált szét élesen a tudományos, a filozófiai és az okkult gondolkozás.

Newton optikája

Newton 1704-ben megjelent „Optika” című művében a színeket a fény részecskéinek nevezte, amely mögött korpuszkuláris kép volt, azaz apró száguldó gömbök voltak szerinte a fény hordozói. Ebben tükröződött általános természetfilozófiája is, ami könyvében megjelenik: „Kezdetben teremté Isten az űrt és az atomokat”. A részecske koncepció azért jelenhetett meg nála, mert előzőleg a golyók ütközési kísérletei segítették a mechanika törvényeinek megalkotásában. Elképzelése szerint valamennyi fizikai törvény mechanikai eredetű, amely erőcentrumokból és azok hatására létrejövő mozgásokból áll. Optikai elképzeléseit prizmával végzett kísérletei alapozták meg, amelyben a fehér fényt alkotó színeire bontotta. Alaposan ellenőrizte, hogy az egyes színek tovább bonthatók-e prizmákkal, lencsékkel és különböző anyagok átvilágításával és kimutatta, hogy ezek a színek nem bonthatók tovább. Ennél is tovább ment, lencsék és prizmák kombinálásával összegyűjtötte az előzőleg szétbontott színeket és kimutatta, hogy az eredmény ismét a fehér szín lett. Ebből egyértelmű lett, hogy a prizma nem alakítja át a fényt, hanem szétbontja összetevőire, amiket ő a fény részecskéinek tekintett.

Newton magyarázata a fénytörésre

Magyarázatot keresett a fénytörés jelenségére is, megadta annak az okát, hogy ha ferdén éri a sugárzás az üveglapot, vagy a prizma felületét, akkor miért törik meg a fény útja más-más szögben a különböző színek esetén. A jelenséget avval magyarázta, hogy sűrűbb közegben eltérő sebességgel mozognak a különböző fényrészecskék. Magyarázata részben megegyezik mai ismereteinkkel, de abban eltér, hogy ő a sűrűbb közegben a fény felgyorsulásáról beszél. Arra nem volt lehetősége, hogy mérje például üvegben, hogy milyen gyorsan halad a fény, ezért a hang eltérő sebességéből indult ki levegőben és vízben. Mint ismert vízben a hang közel négyszer gyorsabban terjed, mint levegőben. Ennek oka, hogy a hang rezgéseket idéz elő és ennek tovaterjedése sebessége attól függ, hogy milyen gyorsan adható tovább ez a rezgési állapot a közegen belül, ami sűrűbb közegben természetesen gyorsabb.

A fény hullámtermészete: az interferencia

Newton azonban olyan kísérleteket is végzett, amely csak a hullámtermészettel volt magyarázható. Vékony üveglapon (planparalell lemezen) vizsgálta a merőlegesen érkező fény visszaverődését, amit az elülső és a hátsó lapról érkező fény együtt határoz meg. A kísérletben fontos, hogy a fény monokromatikus (egyszínű) legyen és pontosan párhuzamos legyen a lap első és hátsó lapja. A lemez vastagsága és a fény színe (ma úgy mondjuk, hogy hullámhossza) határozza meg, hogy mekkora lesz a visszavert fény eredő intenzitása. Ma már ezt fénymérővel pontosan meghatározhatjuk, ami a vastagság függvényében nulla és 16 százalék körül változik, de Newton természetesen ezt még nem határozhatta meg ilyen pontosan. Viszont így is eljutott a fény térbeli periodikus változásának felismeréséhez. Ma ezt a jelenséget nevezzük a fény interferenciájának. Newton nem jutott el a fény hullámtermészetének kimondásához, hanem a térbeli periodikusságot avval magyarázta, hogy a fény részecskéi előrehaladás közben periodikusan változtatják sebességüket.

Fehér fény esetén is fellép az interferencia, ha például nem egyenletes az üveglap vastagsága, akkor annak két oldaláról visszavert fény helyről-helyre másképp találkozik, ami változatos térképet rajzol ki eltérő színekkel. Mindenütt az a szín jelenik meg, amelynek a hullámhossza kedvező a maximális intenzitás létrejöttéhez. Ugyanezért van, hogy az utca kövezetére kifröcskölt olaj, vagy egy felfújt szappanbuborék is változatos színeloszlást hoz létre.

Az éter fogalom megjelenése

Newton felvetette azt a kérdést is, hogy mi az a közeg, amelyben a rezgés tovább terjed. Hang esetén erre könnyű válaszolni, de hogy lehet, hogy a fény nem csak a levegőn, hanem a vákuumon is áthalad szemben a hanggal? Ezt magyarázta avval, hogy van egy a levegőnél is sokkal ritkább közeg, amit éternek nevezett el és ennek rezgései közvetítik a fényt. Az éterben fellépő erőhatásokra adott magyarázata ma már nem tekinthető tudományosnak, ebben megjelennek az okkult gondolkodás elemei is. Erre már kortársai, így a fénytan megalkotásában szintén jelentős szerepet játszó Huygens is (Christiaan Huygens, 1629-1695)  rámutattak.

Az abszolút tér és idő

Newtonnak az éterre vonatkozó koncepciója szorosan kapcsolódik az abszolút térre és időre vonatkozó elképzeléséhez. Úgy fogta fel a mozgást, hogy ez valamilyen abszolút térhez viszonyítható, amiben az idő is egyenletesen, minden hatástól függetlenül folyamatosan halad előre. Kortársai közül ezt fizikai oldalról Descartes bírálta (René Descartes, 1596-1650), aki csak a testek egymáshoz viszonyított mozgásának látta értelmét, hasonlóan gondolkodott Leibniz is (Gottfried Wilhelm Leibniz, 1646-1716), aki rámutatott, hogy az abszolút térhez való viszonyítás mérésekkel nem igazolható. A relativitáselmélet óta tudjuk, hogy a modern fizika ebben a kérdésben Newton bírálóinak adott igazat.

Huygens hullámfelfogása

De ne menjünk el szótlanul Huygens nagyszerű fénytani felismerései mellett sem, akinek a Newton utáni korszak nem ismerte fel eléggé zseniális meglátását a fény hullámtermészetével kapcsolatban. Ő is a mechanikára vezette vissza a fény terjedését, szerinte az éter finom részecskéi egymást meglökve viszik tovább a mozgásállapotot, amely az előrehaladás során minden pontban egy-egy új gömbhullámot gerjeszt, és a gömbhullámok találkozása hozza létre azt a frontvonalat, ami végül a fény egyenes vonalú terjedését idézi elő. A mai fizikában a kvantumelektrodinamikai leírás valójában ezen az elképzelésen alapul, amit nagyon plasztikusan fejt ki Feynman is (Richard Feynman, 1918-1988)  könyvében: „QED: The strange theory of light and matter”.

Huygens a fénytörést a levegő és az üveg határfelületén mai tudásunknak megfelelően magyarázta a hullámok eltérő sebességével operálva, ahol is eltérő a két közegben a fény hullámhossza (azaz a sebesség és a frekvencia hányadosa). A fény a sűrűbb közegbe érve mindig a merőleges irány felé törik meg, amit helyesen azzal magyarázott, hogy sűrűbb közegben a fény lassabban terjed. Figyelemre méltó Huygens magyarázata a kettős törésről: az izlandi mészpátba beeső fény úgy törik meg, hogy kettőzött kép alakul ki. Helyesen mutatott rá, hogy ez a kristály aszimmetrikus szerkezetéből fakad, ami miatt van két irány, ahol eltérő a fény sebessége. Bár Huygens Newtonhoz hasonlóan az éter részecskéinek mozgásából indult ki, de nem ezeknek a részecskéknek a haladásával magyarázta a fényterjedést, hanem a mozgásállapot továbbterjedésével. Mechanikai alapú modelljéből viszont az következne, hogy a fényterjedés longitudinális rezgés, vagyis a haladás irányában valósul meg. A maxwelli elektrodinamikából viszont tudjuk, hogy a fény tranzverzális elektromágneses hullám, azaz merőlegesen rezeg az elektromos és mágneses mező a terjedés irányához képest.

Descartes fényelmélete

A fény mibenlétére Descartes egy harmadik magyarázatot adott. Ő is az éter és a mechanikai modell alapján értelmezte a fényt, szerinte a mindenséget kitöltő finom anyagrészecskék örvénylése gyakorol nyomást a testekre, ami létrehozza azt a hatást, amit fénynek érzékelünk. Ez az elképzelés is gyorsabb haladást tételez fel sűrűbb közegben, amely ellentmond a fénytörés törvényének. Newton ugyanakkor más okból bírálta ezt az elképzelést, rámutatva, hogy ekkor a bolygók és csillagok mozgását is gátolna ez a nyomás, amely súrlódást hozna létre és ezért megváltoznának a bolygómozgás törvényei.

A Fremat-elv

Newton kortársa volt Fermat is (Pierre de Fermat, 1601-1665), akinek  —  optikai eredményei mellett   — az egyik legfontosabb fizikai elv kimondását is köszönhetjük, amit azóta Fermat-elvnek nevezünk. A különböző optikai közegek közötti törésmutató értelmezésére ő adta a legeredetibb magyarázatot. Huygensszel értett egyet abban a kérdésben, hogy a sűrűbb közeg gátolja a fény terjedését és nem elősegíti, ezért ott lassabban terjed. Ő a fény mozgását mint szélsőértéket képzelte el: a fény mindig olyan utat választ, ami biztosítja, hogy a legrövidebb idő alatt érkezzen meg a célba. Azért törik meg a fény iránya, amikor sűrűbb közegbe érkezik, mert bár emiatt a ritkább közegben hosszabb utat tesz meg, de ezt túlkompenzálja, hogy a lassabb közegben rövidebb lesz az út. Evvel lehetett levezetni a korábbi bejegyzésben („Miért kék az ég? Mindennapi fényjelenségek fizikai magyarázata”) már ismertetett fénytörési törvényt.

Gömbhullámok és a fény egyenes vonalú terjedése

Persze felmerül a kérdés: honnan tudja a fény előre, hogy majd átlép egy másik közegbe, ahol lassabban fog haladni? A kérdésre választ Huygensnek a fény terjedését gömbhullámokkal értelmező modellje adja meg. Egyáltalán miért mozog a fény egyenes vonalban, ha gömbhullámokról beszélünk? Azért mert a tér egyes pontjaiban képződő gömbhullámok között interferencia jön létre és az egyenestől eltérő utak esetén a hullámok fázisa szóródni fog, ami interferencia minimumot hoz létre, szemben az egyenes mentén haladó fényutakkal, ahol a fázisok egyezése interferencia maximumot idéz elő. A fény tehát ’letapogatja’ az összes lehetséges utat, de hatása ott jelenik meg, ahova leggyorsabban eljut az interferencia szabálya miatt. Ugyanez érvényesül, amikor a fény sűrűbb közegbe érkezik, ekkor az egyenes úton az eltérő sebesség miatt szóródni fog a gömbhullámok fázisa, kivéve a leggyorsabb haladást biztosító megtört fényutat. Érdemes itt ismét Feynman kvantumelektrodinamikai magyarázatára utalni, aki nyilak összegzési szabályaival szemlélteti a fázisok szóródását a különböző esetekben.

Maxwell egyenletek magyarázata a fényről

Huygens hullámelmélete ellenére a 18. században uralkodóvá vált a newtoni részecske felfogás, ennek oka, hogy Newton követői leegyszerűsítették és abszolutizálták a nagy géniusz elképzeléseit és figyelmen kívül hagyták, hogy maga Newton is megállapította a fény térbeli periodikus viselkedését. A fény mibenlétének értelmezésében a Maxwell által végső formát nyert elektrodinamikai egyenletek hoztak áttörést a hullámfelfogás javára. Erről szól részletesen a „Mi a fény” című korábbi bejegyzés. Ebben az elektromos és mágneses mező fogalmai játsszák a döntő szerepet, amelyek nemcsak az elektromos töltéssel rendelkező objektumok közötti kölcsönhatást írják le, hanem leírják a fény periodikus változását, azaz a hullámokat is, térben és időben.

A foton fogalmának megszületése

Újabb fordulatot hoztak a fény kettős természetének kérdésében a 20. század fizikai felfedezései. A fizika forradalmát idézte elő Planck hipotézise, amikor a feketetest sugárzás kisenergiájú tartományban a végtelenhez tartó intenzitást úgy tudta elkerülni, hogy bevezette a fény energiájának legkisebb egységét, a fotont. Ez visszatérést jelentett a newtoni részecskekoncepcióhoz anélkül, hogy feladta volna a fény hullámtermészetét. A foton olyan részecske, amely rendelkezik h.ν  energiával (h a Planck állandó), h.ν/c = h/λ impulzussal (ν  a frekvencia, λ a hullámhossz) és ℏ=h/2π impulzusnyomatékkal, és ez a részecske c sebességgel halad. Ez utóbbi tulajdonság eltér Huygens koncepciójától, aki a mozgási állapot tovaterjedését képzelte el az éter finom részecskéi között. Az  impulzusnyomaték létezése viszont térbeli forgásokra utal kapcsolódva a Maxwell egyenletekben szereplő forgó elektromos és mágneses mezőkhöz. A fotont úgy fogjuk fel, amely az elektromágneses kölcsönhatás hordozója.

Az éter létezésének cáfolata a relativitáselméletben

A másik fontos felfedezés Michelson (Albert A. Michelson, 1852-1931) és Morley (Edward W. Morley, 1838-1923) nevéhez fűződik, akik kísérletileg cáfolták az éter létezését, mint az abszolút sebesség viszonyítási alapját. Mérésükben az interferencia jelenségét használták fel, hogy kimutassák a fénysebesség állandóságát a Föld keringési irányához képest. Ebből következik Einstein (Albert Einstein, 1879-1955) relativitáselméletének kiinduló pontja, amely szerint newtoni abszolút tér nem létezik, létezik viszont az abszolút sebesség: a fénysebesség, amely bármely inercia (tehát nem gyorsuló) rendszerből nézve ugyanakkora.

A téridő fogalma

A tér és idő elválaszthatatlan egységet alkot, amit felismerve Minkowski (Hermann Minkowski, 1864-1909) bevezette a négydimenziós téridő fogalmát. A tárgyak hossza már nem a descartesi x²+y²+z², lesz hanem a négydimenziós c²t²-x²-y²-z² mennyiség. Az energia és impulzus is egy négydimenziós kovariánsban kapcsolódik össze. A fenti törvényekből az is következik, hogy a megfigyelőhöz képest nagy sebességgel mozgó tárgyak hosszúsága lerövidül (Lorentz kontrakció, Hendrik Lorentz, 1853-1928)) és megnövekszik a tömegük. Különösen fontos az a határeset, amikor a fizikai objektum sebessége eléri a c fénysebességet: ekkor, ha eredetileg lett volna tömege, ez végtelenül nagyra nőne, ha volt valamilyen fizikai kiterjedése, akkor a mozgás irányában ez nullára csökken.

Beszélhetünk-e a foton tömegéről?

A fénysebességű mozgásból következik, hogy a foton nyugalmi tömege nulla! De a relativitáselmélet legfontosabb eredménye szerint az energia és tömeg egyenértékű, amit az E = m.c² összefüggés fejez ki. Ebből az következik, hogy a foton is rendelkezik tömeggel: m = h.ν/c², de ez nem nyugalmi tömeg, hanem a fénysebességű mozgás által létrehozott mozgási tömeg. Tehát a fénysebességű mozgás a tömeg létrehozója. De mi az a fizikai objektum, ami eredetileg nullatömegű volt, de a fénysebességű mozgás által tömegre tesz szert? Itt én nem keresnék étert, vagy valamilyen misztikus ősanyagot, szerintem a tér egyébként nullatömegű pontjai végzik a c sebességű mozgást. Foton esetén két mozgás kapcsolódik össze, az egyik a transzláció, a másik egy rotáció, amelynek frekvenciája a foton szokásos ν  frekvenciája, amelyik megjelenik az energia kifejezésében. A forgás kerületi sebessége is c, amihez az r = c/2πν sugár tartozik. Ez a sugár véges érték és megegyezik a fény hullámhosszával, mert a Lorentz kontrakció csak a mozgás irányában következik be. A véges sugár, a mozgási tömeg és a c kerületi sebesség pedig magyarázatot ad arra, hogy honnan származik a foton impulzusnyomatéka, azaz a spin (Az okfejtés megtalálható egyéb bejegyzésekben is, például „Az elemi részecskék mozgásformái”, vagy „A tér szerkezete és az elemi részecskék mint rezonanciák”).

Honnan származik a fénysebességű forgást fenntartó erő?

De mi azaz erő, amely fenntartja a körforgást, hiszen kompenzálni kell a kifelé húzó centrifugális erőt! Itt lép be az általános relativitáselmélet koncepciója: a tér görbülete a gravitációs erő forrása. A kör kerülete 2r.π az euklideszi geometriában, de a fénysebességű forgásban a kerület nullára csökken. Tehát egy végtelen mértékben torzult geometriáról van szó! Kimutatható, hogy ez pontosan akkora erőt (ezt nevezem erős gravitációnak, lásd a korábban említett bejegyzéseket) hoz létre, amely kiegyenlíti a centrifugális erőt. A magyarázat megfelel a Fermat-elvnek is. A fotont létrehozó sajátmozgás a legrövidebb utat választja, ez pedig a nullakerületű kör, ahol a térpont forog.

A fény kvantumelektrodinamikai koncepciója

A fény legteljesebb modern elmélete a kvantumelektrodinamika. Ez több is, mint a foton elmélete, mert az elektromágneses kölcsönhatást mint a fotonok és töltéshordozók (például az elektronok) együttesét írja le. Ebben minden fotont és minden elektronállapotot egy oszcillátor ír le, amelyek létrejöttét és eltűnését leíró operátorok képezik a kvantálás második szintjét. Az elmélet legnagyobb sikere az elektron anomális mágneses momentumnak kvantitatív értelmezése. Ez a fizikai állandó a fizika történetének legnagyobb pontossággal mért és elméletileg magyarázott állandója. Az elmélet a Feynman által javasolt diagramokra épül, amelyek számba veszik, hogy milyen átmenetek és átalakulások jöhetnek létre az elektronok és fotonok között beleértve a különböző párképződéseket és annihilációs folyamatokat (elektron-pozitron pár létrejötte fotonokból, és ezek annihilációja). Ezek a diagramok a Huygensi elv továbbfejlesztései, ahol virtuális fotonok és elektronok képződnek és tűnnek el a tér egyes pontjaiban (a virtualitás azt jelenti, hogy kísérletileg nem detektált, de a kölcsönhatás mértékét meghatározó folyamatokról van szó). Feynman már idézett könyvében veszi sorra ezeket a lehetséges folyamatokat és mutat rá, hogy ebben sem a fénysebesség, sem az oksági elv nem jelent korlátot. Van például olyan folyamat, ahol egy foton előbb hoz létre egy elektron-pozitron párt, mint ahogy maga létrejön.

A részecskék fénysebességű forgásmodellje

 Feynman arra az álláspontra helyezkedik, hogy nem lehet semmilyen fizikai képet megadni a bonyolult folyamatokra, elégedjünk meg vele, hogy vannak jól működő egyenleteink. A magam részéről nem adnám fel a lehetőséget, hogy konzekvens fizikai képet rendeljek a jelenségekhez, amit már az említett korábbi bejegyzésekben ismertettem. Itt most összefoglalom a modell főbb pontjait.  A fotont, ahogy leírtam, egy csavarmozgás ábrázolja a térben egy henger felületén. Ennek mintájára az elektron is csavarmozgás egy gömbfelületen, ahol két forgás kapcsolódik össze. A két forgás egymáshoz képesti viszonya a jobb és balsodrású királis szimmetriával értelmezhető, ami megfelel a negatív töltésű elektronnak és a pozitív töltésű pozitronnak. Az elektron és pozitron találkozása annihilációhoz vezet, mert ekkor az ellentétes kiralitású két ’másodlagos’ forgás kioltja egymást és az így megmaradó egyszeres forgás épp a fotonnak felel meg. A fénysebességű forgások nullafelületű gömböt hoznak létre összhangban az elektron és pozitron szórás kísérletekkel (Bhabha-szórás, Homi K. Bhabha, 1909-1966), amely szerint a részecske töltése pontszerű eloszlással rendelkezik. Az elektron spinje fele a fotonénak, mert az erős gravitációnak két különböző forgásból származó centrifugális erőt kell kiegyenlíteni. Már számos kísérlettel igazolták, hogy a fotonhoz hasonlóan az elektron, a proton, sőt kisebb molekulák is kettős természettel rendelkeznek, egyaránt viselkednek korpuszkulaként és hullámként. Az interferencia jelenség hullámhossza a Compton hullámhossz (Arthur H. Compton, 1892-1962), amely a nyugalmi tömegből számítható ki a l = h/m.c összefüggés alapján. Az elektron fénysebességű forgásmodellje ezt a hullámhosszat a forgás sugaraként értelmezi, amely meghatározza az elektron-hullám interferenciaképét.

Virtuális részecskék a virtuális térben

Hogyan kapcsolhatjuk fizikai világképünkhöz a kvantumelektrodinamika virtuális folyamatait? Kétségtelen, hogy szükséges számba venni ezeket a folyamatokat, ha az elektron és a mágneses mező kölcsönhatását helyesen akarjuk leírni, viszont mivel nem detektálható folyamatokról van szó, így az a tér és idő, amelyben leírjuk a folyamatokat szintén virtuális. Ezt a virtuális teret és időt már nem korlátozzák azok a törvények, amelyet a valódi kölcsönhatásokon keresztül ismertünk meg, ezért nem vonatkozik rájuk az oksági elv és a fénysebesség átléphetetlenségi szabálya sem. 

Összefoglaló megjegyzés

Az elemi részecskék és a fény kettős természetére szemléletes magyarázatot ad a fénysebességű forgások modellje. A hullámtermészet onnan származik, hogy minden részecske, így a foton is fénysebességű forgásokat végez, melynek fázisegyezése alakítja ki az interferencia maximumokat. A fénysebességű forgáshoz azonban véges sugár és tértartomány tartozik, ez reprezentálja a korpuszkuláris tulajdonságokat, a tömeget, az impulzus és az impulzusnyomatékot.

A blog egyéb írásainak összefoglalója a megfelelő linkekkel együtt a „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv” című bejegyzésben található meg.

A tudomány nemzetközisége

Azt aligha kell indokolni, hogy miért fontos angol nyelven publikálni az új tudományos eredményeket. A tudomány nemzetközi, aki be akar kapcsolódni a tudomány vérkeringésébe, az nem tehet mást, minthogy eredményeit angol nyelven teszi közzé. Az egyéb nemzeti nyelven írt munkák csak sokkal szűkebb körben jutnak el a kutatókhoz, azokra nem érkezik sok hivatkozás, azok a tudomány perifériájára kerülnek.

A tudomány centruma Európából az USA-ba került

 Ez nem volt így még a XX. század első felében, jelentős eredményekről számoltak be a patinás német folyóiratok, gondoljunk csak Einstein legfontosabb publikációira, de nem sokkal maradtak el ettől a francia, olasz és orosz nyelvű közlemények sem. Több jelentős eredmény látott először napvilágot magyar folyóiratokban is.  Ekkor még Európa volt a tudomány központja. A második világháború azonban jelentős változást hozott. Sok kitűnő európai tudós ment ki az Egyesült Államokba, köztük jelentős magyar tudósok is, néhányan még Nobel díjban is részesültek. Ezek a tudósok már az amerikai egyetemeken adták tovább tudásukat hozzájárulva az ottani egyetemek felvirágzásához, miközben Európában lecsökkent a nemzeti egyetemek vonzereje, visszaesett a kutatás színvonala a helyi kutatócentrumokban is. Ennek hatása pedig továbbgyűrűzik a technikai fejlődésben és az innovációban is.

Tudományos szakcikkek és tudománynépszerűsítés

Az angol nyelv dominanciája ma már olyan erős, hogy nem érdemes és nem lehet dacolni vele, de nem szabad, hogy ez a magyar nyelvű szakirodalom elsorvadásához vezessen. A szakirodalom alatt nem csak tudományos publikációkat értek, mert legalább ilyen fontosak azok az írások, amelyek szélesebb publikum számára továbbítják a korszerű tudományos ismereteket. A szakemberek számára írt tudományos cikkekben az a fontos, ami megmutatja az újdonságot a szerzők munkájában az egyes tudományterületen. Az ilyen cikkek megfogalmazása azonban nem követhető a tudomány iránt érdeklődő, de az adott speciális területen nem járatos olvasók előtt. Szükség van ezért más csatornákra is, ahol nem okvetlenül az újdonság, sokkal inkább a közvetítés a legfontosabb. A legnehezebb természetesen megtalálni a helyes arányt a szakszerűség és a népszerűsítő szándék között. A leegyszerűsített magyarázatok talán könnyebben érthetők, de ha ez a szakszerűség rovására megy, akkor az ilyen írások több kárt okoznak, mint hasznot. Főleg azért, mert a szakszerűség háttérbe szorulása teret adhat a burjánzó áltudományos nézeteknek.

Írjunk közösen blogot a természettudományról

Már jó egy éve, 2015 május végén indítottam el egy blogot „A fizika kalandja„  címmel. Célom kettős volt, bemutatni egy olyan fizikai elképzelést, amelyben az általános relativitáselmélet adja az alapot a részecskefizika számára is. Emellett közelebb akartam hozni a köznapi gondolkozáshoz a kvantummechanika és a relativitáselmélet sokszor nehezen felfogható világát. Mennyire sikerült megtalálni a helyes arányt a szakmai hitelesség és a közérthetőség szándéka között? Egyes írásokban a szakmai precizitásra való törekvés dominált, másutt a közérthetőség igénye. Amit sikernek tartok, hogy a letöltések száma mára átlépte a 10 000-es küszöböt. Ez számomra is mérföldkő, ami felveti a kérdést, hogyan tovább? Ebben az adna további lökést, ha nem csak a saját írásaim, gondolataim jelennének meg a blogban. Szívesen venném, ha a blog szelleméhez illő bejegyzéseket másoktól is kapnék, amit felvihetnék a portálra. Biztos vagyok benne, hogy sokan tudnának kifejteni olyan gondolatokat, amelyek közzététele sokak érdeklődésével találkozna. Ha pedig beindulna ez a folyamat, az lendületet adhatna az oktatásnak, fokozódna az érdeklődés a tudományos és technikai eredmények iránt. Ez hozzájárulna a magyar technikai kultúra magasabb szintre emelkedéséhez és kikerülnénk abból a mélypontból, ami ma a hazai innovációt jellemzi.

rockenbauer.antal@ttk.mta.hu

A blog korábbi írásait összegzi a linkek megadásával a „Paradigmaváltás a fizikában: téridő kontra kvantumelv” című bejegyzés.

Elemi részecskék a Standard Modellben

Az elemi részecskékről szerzett ismereteinket összegző Standard Modell szerint az alcímben feltett kérdésre a válasz: HÁROM. Ez azt jelenti, hogy három-három elektron illetve neutrínó típusú lepton létezik, nevezetesen az elektron és antirészecske párja a pozitron, továbbá a müon és a tauon, szintén antirészecske párjukkal együtt. Evvel összhangban három generációja van a kvarkoknak is (u és d az első, c és s a második, míg t és b a harmadik szinten, lásd erről részletesebben a „Barangolás a kvarkok és elemi részecskék világában”). A kvarkoknak ez a három generációja építi fel az összes eddig megfigyelt hadront (azaz a három kvarkból, vagy antikvarkból felépülő barionokat, illetve a kvark-antikvark kombinációkat tartalmazó mezonokat). Ez a három generáció teljesen lefedi a kísérletileg megfigyelt elemi részecskék családját. A kérdést azonban fel lehet tenni: vajon már ismerjük az összes lehetséges elemi részecskét?

Lehetnek-e negyedik generációs részecskék?

A Standard Modellnek azonban nincs olyan elméleti alapja, amely kizárná, hogy lehetséges lenne egy negyedik generáció is. Ennek azért van jelentősége, mert a megfigyelt részecskék száma a jelenlegi technikai feltételektől függ, ennek továbbfejlődése lehetővé teheti a még rövidebb (10^-24s alatti) és a még kisebb gyakorisággal képződő új részecskék detektálását, és kérdés, hogy ezek az új részecskék a már létező elméleti keretekbe illeszkednek, azt megerősítik, vagy cáfolják-e. A lehetőségek közé tartozik például a negyedik generációs elektron-típusú részecskék megfigyelése, vagy olyan hadronoké, amely már igényli további kvarkok feltételezését. A jelenlegi LHC kísérletek elsősorban a Higgs-féle szimmetriatörési koncepció (Higgs bozon), illetve a szuperszimmetria (SUZY) elméletek alátámasztására törekszenek, de egyáltalán nem biztos, hogy az új kísérleti eredmények az előzetes elméleteket fogják alátámasztani és nem új koncepció kidolgozását teszik szükségessé. Én személy szerint az utóbbinak adnék nagyobb esélyt.

Az elektron család tagjai

A negyedik generáció lehetőségének megvizsgálása érdekében nézzük meg az elektron család három tagjának tulajdonságait. Ezek a részecskék valóban elemiek, azaz tovább nem oszthatók jelenlegi tudásunk szerint. Ezt alátámasztják a szóráskísérletek (Bhabha szórás, amikor elektronokat bombáznak pozitronokkal), mert eszerint a töltés pontszerű eloszlással rendelkezik, szemben például a protonokkal, ahol a töltéseloszlás sugara véges értékű (10^-13cm). Egy pontszerű részecske pedig aligha osztható tovább.

Az elektron, a müon és a tauon egyaránt egységnyi negatív töltéssel és S = ½ spinnel rendelkezik, a különbség köztük a tömegben és a részecske stabilitásában van. Az elektron tömege 0,511 MeV (ez pontosabban az m.c² sajátenergia) és a részecske stabilis. A stabilitás abból fakad, hogy az elektronnak nincs „hova” tovább bomlani, mert nincs az elektronnál kisebb tömegű töltéssel bíró részecske. A müon tömege 105,7 MeV és bomlásának felezési ideje 2,2x10^-6 s, a tauon esetén a két adat 1777 MeV és 3x10^-13s. A Standard Modell azonban nem ad eligazítást, hogy miért pont ekkorák ezek az értékek, azaz nincs arra becslés, hogy mekkora lenne a negyedik generációs részecske  (nevezzük a továbbiakban transz tauonnak)  tömege és milyen hosszú lenne az élettartama. A müon 207-szer nehezebb az elektronnál, a tauon pedig 17-szer nehezebb a müonnál, amiért az transz tauon tömegét valahol a 10 GeV tartományban képzelhetjük el, azaz összemérhető tömegű lehet a legnehezebb hadronokkal. Az élettartama, ha annyival rövidebb a tauonnál, mint amennyivel az rövidebb a müonnál, akkor 10^-20s körül lehetne, ami jócskán hosszabb, mint a kísérletileg még detektálható 10^-24s határ. Ez azonban teljesen önkényes feltevés, hiszen lehet ennél jóval rövidebb is, ami már alatta van a mérhető értéknek. Az adatok elemzése ezért nem ad lehetőséget arra, hogy eldöntsük létezhet-e ez a negyedik generációs részecske.

Bizonytalansági reláció és a részecskék kimutathatósága

Vizsgáljuk meg a kérdést a kvantummechanikai bizonytalansági elv oldaláról is. A mikrorendszer energiájának mérési pontosságát behatárolja, hogy a rendszer állapota mennyi ideig tekinthető változatlannak:

ΔtxΔE ≥ h/2

ahol h = 6,626x10^-34 J.s, a Planck állandó. Az energia és tömeg E = m.c² ekvivalenciája miatt ez egyúttal meghatározza a részecske tömegmérési pontosságát is. A részecskét akkor tudjuk detektálni, ha a tömegmérés hibája kisebb, mint maga a nyugalmi tömeg, ezért az m tömegű részecskét akkor tudjuk kimutatni, ha az élettartamára fennáll a következő szabály:

Δt ≥ h/2m.c²

A 10 GeV = 1,6x10^-9J sajátenergiájú részecskénél ez azt jelenti, hogy a detektálás akkor valósítható meg, ha az élettartam hossza legalább 2x10^-25s. Ez jelenleg a mérési határ alatt van.

Az elemi részecskék fénysebességű forgásmodellje

Hasonló következtetéshez juthatunk a már több bejegyzésben ismertetett fénysebességű forgásmodellben is ( Lásd pl. „A tér szerkezete és az elemi részecskék mint rezonanciák”). Ez a modell a fotonokat mint egytengelyű fénysebességű forgásokat, az elektronokat mint kéttengelyű gömbi forgásokat értelmezi, ahol a tömeget a forgás frekvenciája határozza meg. Elektronoknál a forgás megkettőződése miatt

h.ν = ℏ.ω = 2m.c²

Itt ν a frekvenciát, ω a körfrekvenciát jelöli. A modell a kvantumot mint a fénysebességű forgás impulzusnyomatékát értelmezi, amely körforgásnál (ilyen a foton) ℏ, míg gömbforgásnál (pl. az elektron) ℏ/2. A kvantum, illetve a részecske csak akkor jöhet létre, ha legalább egy fordulat végbemegy, azaz a részecske élettartama legalább olyan hosszú, mint ami szükséges egy fordulat megtételéhez. Ez azt jelenti, hogy a T = 1/ν élettartam hossza:

T ≥ h/2m.c²

összhangban a bizonytalansági elvvel.

A részecske sajátforgásának stabilizáló ereje: az erős gravitáció

A fénysebességű forgásmodell az általános relativitáselmélet alapelvét kiterjeszti az elemi részecskékre is, amikor a téridő extrém görbületére vezeti vissza a sajátforgások centrifugális erejét ellensúlyozó centripetális erőt (Lásd: „Térgörbület és gravitáció forgó rendszerekben”). Ez az erő, az erős gravitáció, amely r sugarú forgás esetén ℏ.c/r², amely pontosan kiegyenlíti az m.ω²r = m.c²/r  centrifugális erőt. A két erő egyenlőségéből fakad, hogy ℏ=m.r.c  (ez épp az impulzusnyomaték definíciója), azaz a fénysebességű körforgás impulzusnyomatéka a ℏ redukált Planck állandó. Kettősforgásnál kétszer akkora centrifugális erőt ellensúlyoz az erős gravitáció, amiért elektron esetén feleződik az impulzusnyomaték, azaz a spin ½ értéket vesz fel.

A gyenge kölcsönhatás szerepe a részecskék átalakulásában

Körforgások, azaz a fotonok esetén a frekvencia tetszőleges lehet, míg a kettősforgás csak három frekvencián fordul elő: az elektron, a müon és a tauon esetén. Ezt úgy értelmezhetjük, hogy a téridőben a kétféle forgás rezonanciája hozza létre a részecskéket. Ezt a forgásmodellt párhuzamba állíthatjuk az atommagok körül pályamozgást végző elektronok esetével, ahol kötött állapotban diszkrét energiájú állapotok jönnek létre. Ennek okát a „Foton: a mikrovilág postása és szabályozója” című bejegyzésben avval adtuk meg, hogy a fotonok csak ℏ egységnyi impulzusnyomatékot adhatnak át az elektronoknak, amiért az elektronok pálya impulzusnyomatéka ℏ egészszámú többszörösét veszi fel, amihez viszont diszkrét energiaértékek tartoznak. Alkalmazzuk ezt a képet az elektroncsalád tagjaira is! Tekintsük úgy a müont és a tauont, mint az elektron gerjesztett állapotát, ahol azonban a gerjesztést nem a fotonok végzik, hanem a gyenge kölcsönhatás közvetítői, a W  és Z  bozonok. Ez összhangban van a müon bomlási mechanizmusával, mely szerint első lépésben a müonból egy W^- bozon és egy müon neutrínó lép ki, majd második lépésben a W^- bozon alakul át elektronná egy neutrínó kilépésével együtt. A tauon bomlása ennél egy lépcsővel összetettebb, mert ekkor először a tauon bomlik el müonra a W^- bozon és egy tauon típusú neutrínó kilépésével. (A Standard Modell antineutrínókról beszél, de a forgásmodell szerint ez nem különbözik a neutrínótól).

Az elektromágneses és gyenge kölcsönhatás elméletének egyesítése

Az elméleti fizika egyik legnagyobb sikere (Glashow-Salam-Weinberg,1968), hogy sikerült egységbe kovácsolni két független elméletet, az egyik az elektromágneses kölcsönhatás kvantumelmélete, a kvantumelektrodinamika, a másik a gyenge kölcsönhatás kvantumelmélete. A közös elmélet az elektro-gyenge kölcsönhatás mezőelmélete. Ebben a foton, a két W  bozon és a Z  bozon egyetlen „részecskecsalád” négy eleme, amely együttesen írja le az említett két kölcsönhatást. Ennek az egyesített elméletnek felel meg a fénysebességű forgásmodellben az elképzelés, hogy amíg a foton mozgásában a körmozgás úgy kapcsolódik a haladó mozgáshoz, hogy ennek iránya párhuzamos a forgástengellyel, addig a W  bozonoknál a haladási irány és a forgástengely merőleges egymásra (Lásd: „A gyenge kölcsönhatás kiválasztási szabályai és a CPT tükrözés”).  A Z  bozon a W^- és W⁺  bozonok szuperpozíciós állapota, ami ezért nem rendelkezik elektromos töltéssel. Ennek megfelelően a foton mozgása egy csavarpályát ír le, amíg a W  bozonoké egy táguló spirálpálya. A spirálpályán a sugár növekedése a fénysebesség miatt csökkenő frekvenciát és ennek megfelelően csökkenő tömeget hoz létre. Amíg a fotonnál a haladási irány párhuzamossága a tengellyel nem hoz létre Coriolis erőt és így elektromos töltést sem, addig a W  bozonoknál a két irány merőleges, amiért töltött részecskékről van szó, ahol a töltés előjele a mozgás jobb- illetve balkezes térbeli szimmetriájának felel meg.

Az elektro-gyenge kölcsönhatás és a részecskék negyedik generációja

A spirálpályán mozgó W  bozonok frekvenciaváltozása miatt fellép az Euler típusú tehetetlenségi erő (lásd: „Az elektro-gyenge kölcsönhatás és az elemi részecskék átalalkulása”), ami egyrészt létrehozza a gyenge kölcsönhatási erőt, másrészt a frekvenciaváltó képesség rezonanciát hoz létre a különböző tömegű és forgási frekvenciájú elemi részecskék között.  A W  bozon nagy tömege (80,39 GeV) lehetővé teszi, hogy a tágulási folyamat során létrejöjjön a rezonancia az egymásba alakuló részecskék között. Ha létezik transz tauon is, melynek a várható nagyságrendje 10 GeV tartományban lehet, akkor a W  bozon ennek bomlását is előidézheti, azaz a gyenge kölcsönhatás elmélete sem zárja ki az elemi részecskék negyedik generációjának létezését.  Csábító lehetőségnek látszik az elektro-gyenge kölcsönhatás mezőelméletének továbbfejlesztése, amelyben építve a W  bozonok rezonanciaközvetítő szerepére, olyan mechanizmust lehetne felállítani, amely meghatározná a müon és tauon tömegét mint az elektronok sajátforgásának gerjesztett állapotait. Ez az elmélet adhatna végső választ arra a kérdésre is, hogy léteznek-e negyedik generációs elemi részecskék.

A bejegyzésben a részecskék negyedik generációjának lehetőségét vizsgáltuk meg, de természetesen a nagyenergiájú vizsgálatok egészen más irányban is adhatnak lökést a részecskemodellek továbbfejlesztésére.

A blog korábbi írásait összegzi a linkek megadásával a „Paradigmaváltás a fizikában: téridő kontra kvantumelv” című bejegyzés.