Elektron-pozitron annihiláció és a Pauli-féle kizárási elv

A fermionok fénysebességű forgásmodelljében a kettős forgások jobb és balsodrású kiralitásával értelmeztük a részecske-antirészecske kettősséget [1]. Az elektron negatív és a pozitron pozitív töltése is az eltérő kiralitással magyarázható. mert ekkor a két forgás egymásra ható Coriolis ereje fordított irányú.

Az elektronok egymás közötti kölcsönhatását (Pauli-féle kizárási elv) illetve az elektronok és pozitronok közötti annihilációt egyaránt a Coulomb-kölcsönhatással magyarázhatjuk. Két elektron nem lehet azonos kvantummechanikai állapotban a Pauli-féle kizárási törvény szerint. Ez azt jelenti, hogy két együttforgó és azonos kiralitású fermion nem lehet egyidejűleg a tér azonos pontján, mert ebben az esetben a szinkronmozgás végtelenül nagy Coulomb-taszítást hozna létre. A neutrínó esetén kérdéses a Pauli-elv érvényessége, mert az elektromágneses és erős kölcsönhatások hiánya miatt nem tudunk kötött neutrínó állapotot létrehozni. Töltés semleges összetett objektumokban (például neutronokban) az összetevő kvarkok elektromos taszítása akadályozhatja meg, hogy a részecskék kvantummechanikai állapota megegyezzék. Másfelől ha két különböző kiralitású és azonos tömegű részecske lenne egy pozícióban (például egy proton és egy antiproton), akkor a Coulomb-kölcsönhatás végtelenül nagy vonzóerőt hozna létre. Ez sem lehetséges, a két részecske ekkor annihilál és fotonokat bocsát ki. A csavarmozgási modell szerint ez azt jelenti, hogy a kétdimenziós forgásokból az egyik komponens kioltódik és így kettős forgás helyett egytengelyű forgások – azaz fotonok – keletkeznek. Két ellentétes töltésű, de eltérő tömegű elemi részecske azonban lehet egy helyen, erre példa, hogy a Hidrogén atom magjában az „s” elektron véges valószínűséggel tartózkodik, amit úgy interpretálunk, hogy ekkor a forgások nem kerülhetnek szinkronba az eltérő frekvencia miatt.

Az annihiláció fordított folyamata is létezik, például nagy energiájú fotonok töltött objektumokkal való kölcsönhatása kiválthatja elektron-pozitron párok képződését. Ez a folyamat a kiralitás megmaradás törvényének engedelmeskedik, amikor a képződő részecske párban a „második” forgások ellentett sodrásirányban kapcsolódnak az elsőhöz. 

 A gyenge és az elektro-gyenge kölcsönhatás 

Az elektromágneses kölcsönhatástól nagymértékben eltér a részecske típusok átalakítását előidéző gyenge kölcsönhatás. Ennek egyik formája a neutronok béta bomlása, amelyik a fizika egyik legkülönösebb jelensége, mert a többi fizikai kölcsönhatásban megfigyelhetetlen tulajdonságokkal rendelkezik. Egyik ezek közül a paritássértés, amit a forgás modellben a sajátforgások szimmetriatulajdonságára, a kiralitásra vezettünk vissza [2]. Van a jelenségnek egy még furcsább tulajdonsága, ami a bomlás kétlépcsős jellegéhez kapcsolódik. Az első lépésben a neutronból úgy lesz proton, illetve a Standard Modell szerint a -1/3e töltésű down kvarkból a +2/3e töltésű up kvark, hogy eközben kilép egy negatív töltésű ħ impulzusmomentumú (tehát S = 1 spinű) részecske is, amit W^- bozonnak neveztek el. Ez a bozon különös tulajdonságokkal rendelkezik, mert a tömege (80,385 GeV) közel százszor haladja meg a kibocsátó neutron tömegét és élettartama rendkívül rövid, nem haladja meg a 10^-24 másodpercet. Higgs a spontán szimmetriatörés koncepciójával magyarázza a nagy tömegű W^- bozon létrejöttél: az eredetileg szimmetrikus tér metastabil állapotot jelent, mint amikor egy golyót helyezünk el a körkörösen szimmetrikus mexikói kalap tetején, ahonnan a golyó bármelyik irányban legurulhat. A legurulás már kiválaszt egy irányt, ettől törik meg a szimmetria és a képződő részecske energiája a szimmetrikus és aszimmetrikus állapotok energiakülönbségének felel meg.

Az általam javasolt modell párhuzamba hozható Higgs elképzelésével. Az egyenes koordinátákból álló és transzlációs szimmetriával rendelkező euklideszi térben létrejöhetnek éles „begyűrődések”, ahol –m.c² mélységű a tér görbületéhez tartozó potenciális energia. Ez stabilizálja a bozont, amelynek spinje megegyezik a fotonéval, azaz ez a részecske is egydimenziós forgásból épül fel. Ennek a bozonnak rendkívül rövid az élettartama, ezért még a fény c sebességével haladva sem tehet meg hosszabb utat, mint 10^-16 m, ez a távolság pedig egy nagyságrenddel kisebb, mint a nukleonok sugara. A W bozonok sajátmozgását a fotonhoz hasonlóan úgy fogjuk fel mint egy forgás és egy transzláció kombinációját, de amíg a foton a forgástengely mentén halad, a W bozonoknál a haladás sugár irányú, azaz merőleges a forgástengelyre. A merőlegesség következtében fel lép a Coriolis-erő, ami magyarázza, hogy miért rendelkezik a W bozon ugyanakkora töltéssel, mint az elektron. A W bozonnak a fotonhoz hasonlóan két polarizációs iránya van, az egyikhez pozitív, a másikhoz negatív töltés tartozik a Coriolis-erő irányának megfordulása miatt.  A sugár fénysebességű növekedése spirális pályát hoz létre, mely szerint:

R_c(t) = R₀ + c.t

ahol R₀ a képződő bozon kezdeti sugara. Az R_c(t).ω = c  szabály miatt időben csökken az ω körfrekvencia és a tömeg:

 és

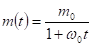
A fenti összefüggésekben ω₀ és m₀ a bozon kezdeti körfrekvenciája és tömege. A W bozon tömege sokszorosa az elektronénak (157 310-szer nagyobb), ezért azaz idő, ami alatt lecsökken az eredeti tömeg az elektron tömegének értékére gyakorlatilag csak az elektron de Broglie frekvenciájától függ, annak reciprokával egyezik meg:

t_el = ℏ/m_el.c² = 2,57x10^-21 s.

Az elfordulás fázisa a kezdő pozícióhoz képest logaritmikusan változik:

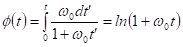
Az elektron kialakulásáig megtett fázisváltozás φ_el = ln(1 + m_W/m_el) = 11,97 radián, ami nem egészen két fordulatnak felel meg.

 Amikor a tömeg értéke eléri az elektronét, vagy legalábbis megközelíti azt, létrejön az elektronból és neutrínóból álló fermion pár. A W bozon spirális pályáját az ábra sorozaton mutatjuk be.

Folytatás a második részben: Az elektro-gyenge kölcsönhatás és a részecskék átalakulása_II

1. Lásd „A részecske fizika nyitott kérdései I és II” , illetve „A screw model for quantum electrodynamics” c. bejegyzéseket
2. A blog további begyzéseinek összefoglalóját lásd "Paradigmaváltás a fizikában"