Absztrakt

Gondolatkísérlet az idő kozmológiai fogalmának átértelmezésére. Az ősrobbanás elmélete szerint az első másodpercben nagyobb átalakulásban ment át az univerzum, mint az azt követő sok milliárd év alatt. Az események exponenciális sűrűsége helyettesíthető egy olyan időfogalommal, amelynek kezdeti exponenciális jellege egyenlíti ki az események sűrűségét.  Ez olyan kérdéseket vet fel, hogyan térhetünk át a szokásos lineáris időfogalomról az exponenciális lefutásra, ez hogyan tükröződik a tér szerkezetében, mi történik a fizikai kölcsönhatások állandóival, melyek maradnak ugyanazok és melyek változnak meg? Megvizsgálásra kerül az időtranszformáció és a kvantummechanika kapcsolata is.

Bevezetés

Itt élünk a Földön, 13,78 milliárd évvel az univerzum létrejötte után, a Naprendszer harmadik bolygóján, és amit átélhetünk az néhány évtized. Éltető Napunk a Tejút százmilliárd csillagjának szerény képviselője, de Tejútunk is csak egyike a több száz milliárd galaxisnak. Az időnek és térnek ebből a parányi tartományából vajon milyen messzire láthatunk el? Az ősrobbanás első másodpercének hihetetlen sebessége, amikor több minden történt az első másodpercben, mint utána 13,78 milliárd év alatt, leírható-e a szokásos időfogalmunkkal, vagy indokolt-e az időmúlás változó sebességéről beszélni? Ezekről a kérdésekről fejtek ki néhány gondolatot.

Lineáristól a nemlineáris extrapolációig

Az univerzum számunkra belátható tartományában arányosan növekvő távolsággal és arányosan múló idővel találkozhatunk, ez meghatározza gondolkodásunkat is, ami lineáris extrapolációhoz vezet. Az extrapoláció során jelenünk változásait messzire előre vetítjük, de ugyanezt tesszük, ha a távoli múlt leírására vállalkozunk. A lineáris extrapolációt egy matematikai tételre alapozzuk: kiindulva valamilyen függvényből, legyen az exponenciális, logaritmikus, vagy bármilyen, ha csak egy parányi szakaszt nézünk, az jól közelíthető egyenessel is. A lineáris gondolkodást tükrözi Euklidesz geometriája is, amelyen rést ütött Bolyai lángelméje, amikor felvetette, hogy hosszabb távon szétpattanhatnak a párhuzamos egyenesek. Kepler és Newton mechanikája is a lineáris gondolkodás példája, melyben a sebességek lineárisan adódnak össze térben és időben. Ez jól megfelel hétköznapi tapasztalatainknak, ahol a mozgási sebesség nagyon távol van a fény sebességétől, de a modern fizika eszköztára a részecskék világában, már felgyorsíthatja a mikrovilág parányait olyan sebességre, ami közel kerül a fényéhez. Ebben a tartományban már nem érvényesek a mozgás megszokott szabályai, amit a speciális relativitáselmélet nemlineáris sebesség összeadási szabálya fejez ki. Ezt az elvet vitte tovább Einstein, amikor a gravitáció mozgásegyenletét a tér és idő koordináták nemlineáris dimenziójában fogalmazta meg. Így vált a modern fizika szemléletének alapjává a nemlineáris gondolkodás, melyben olyan fizikai világképhez jutunk, ahol a tér és idő nem csak keretet ad a változásnak, hanem maga is változik. Ennek jegyében teszünk kísérletet, hogy a nemlineáris szemléletet kozmológiai távlatokra terjesszük ki!

Lineáris és exponenciális idő

Kezdjük hát az idővel! Mértékegységét a Föld forgásához és keringéséhez kötjük, mert a mozgások ismétlődése eszközt ad, hogy ezzel skálázzuk a történteket, beszélhetünk arról, hogy mi volt előbb és mi volt utóbb. Ez az idő azon a közmegegyezésen alapul, hogy az ismétlődő mozgások hosszúsága azonos. Ez logikus alapja lineáris időfogalmunknak, de mégiscsak egy posztulátum! Azt is elképzelhetjük, hogy az ismétlődő periódusoknak más és más az időtartama, például valamilyen szabály szerint növekedhet, csak ez rövidtávon nem figyelhető meg. Az einsteini gravitációs elmélet szerint ez nem is olyan abszurd, mert a téridő görbülete az időt is érinti, igaz hogy csak lokálisan.

Ha nem lépünk messzire vissza az időben, lineáris időfogalmunkkal nincs is semmi baj, de megváltozik a helyzet, ha a kozmológia ősrobbanás koncepciójára gondolunk. Az egyik alapvető megállapítás szerint az univerzum első másodpercében nagyobb változáson esett át, mint az azt követő 13,78 milliárd év alatt. De itt álljunk meg egy pillanatra! Honnan származik az egy másodperces időtartam? Ez a Föld tengelyforgásához igazodik, ami a nap 86 400-ad részét jelenti. Ezt ugyan az atomórák korszakában pontosítani kellett a nap hosszának ingadozása miatt, amiért jelenleg a másodpercet egy atom sugárzásának frekvenciájához kötjük (a ¹³³Ce cézium atom alapállapotában kibocsátott fény 9 192 631 770 számú periódusa), de így is egy periodikus jelenségen alapul az időtartam egysége. Az ősrobbanás korai szakaszában nem létezett se a forgó Föld, se a Nap, vagy a Tejút, de még az atomok sem alakultak ki, miért támaszkodunk mégis olyan időegységre, amely semmilyen szinten nem köthető az akkori univerzumhoz? Elvben olyan időfogalmat illene használni, amely az adott korszak mozgásformáit hasonlítja össze, vagyis a korszak mozgásaihoz kapcsolódó „másodperc” definíciójára lenne szükség. A problémát az jelenti, hogy nincs módunk az univerzum ősi korszakának közvetlen megfigyelésére, ezért a jelenünk időegységét extrapoláljuk a múltba. Az idő mértékének lineáris felfogása helyett alakítsuk úgy át időfogalmunkat, hogy lépést tartson az univerzum átalakulási sebességének változásával. Ez azt jelenti, hogy nem az egy másodperc alatt bekövetkező változások száma lesz nagy az ősrobbanást követően, hanem állandó marad az eseményszám, és az egységnyi időtartam hossza lesz rendkívül rövid. A mozgások sebességét az idő reciprokával, a frekvenciával jellemezhetjük. Az univerzum egyes korszakaihoz valamilyen karakterisztikus frekvenciát rendelhetünk, amely rendkívül nagy volt a kezdetekben, és fokozatosan csökkent a konszolidált univerzumban.  Az ősrobbanás utáni univerzum gyors exponenciális változását az exponenciális jelleg kompenzációjával valósíthatjuk meg, vagyis a lineáris időfogalomról áttérünk az exponenciálisan változó időfogalomra. Ennek keretében az univerzum korával csökken a karakterisztikus frekvencia, vagyis hosszabbodik az idő egysége a másodperc is.  A periodikusan ismétlődő mozgások esetén ez azt jelenti, hogy az egymást követő ciklusok időtartalma hosszabbodni fog. A frekvencia és az időegység olyan transzformációját végezzük el, amely az univerzum jelenlegi korát veszi alapul, a jövő felé pedig kisebb mozgási frekvenciát határoz meg, azaz lassulni fog az idő múlása; viszont a múlt felé haladva megfordul a dolog, akkor rövidebb periódusokban méri az események hosszát, az első másodpercben különösen drámai mértékben húzza szét időben a robbanásszerű események skáláját. Az ennek megfelelő exponenciális transzformáció a következő lehet:

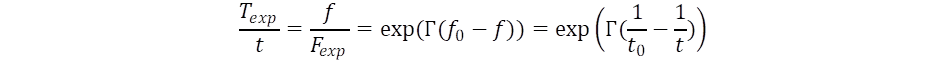
Itt a Γ faktor adja meg az idő karakterisztika „ütemtervét”, f és f₀ az univerzum korábbi és mai korszakának karakterisztikus frekvenciája, míg t jelöli az univerzum szokásos (lineáris idejű) korát, végül t₀ felel meg a jelenkornak ugyanebben a dimenzióban, vagyis 13,78 milliárd év az ősrobbanás óta, ami másodpercekben megadva 4,35·10¹⁷.

A fenti formulában az f₀ frekvencia tulajdonképpen a Hubble állandó 1/s egységben kifejezve, f =1/t pedig az univerzum korának reciproka, amely csak „most” azonos a Hubble állandóval. Ennek oka, hogy a frekvenciadimenziójú f csökken az univerzum korával, míg a kozmológia szerint az univerzum gyorsulva tágul. T_exp és F_exp a transzformált idő és frekvencia, amit nevezhetünk az univerzum exponenciális idejének, illetve karakterisztikus frekvenciájának.

Az idő transzformációja

A fenti időtranszformációt nevezhetjük az univerzum exponenciális lassulási törvényének is, ez viszont felveti a kérdést, hogy a transzformációs szabály hogyan igazodik a fizika törvényeihez? Először is nézzük meg a megváltozott időskála legfőbb sajátságait!

Amikor t = t₀ a kitevő nulla lesz és T_exp = t₀, illetve F_exp = f_o. Amikor t > t₀, vagyis a jövőbe nézünk, akkor pozitív a kitevő, vagyis T_exp > t és F_exp < f_o, ez felel meg az idő meghosszabbodásának, illetve a lassuló karakterisztikus frekvenciának; míg ha t < t₀, az már a múlt, ahol negatív a kitevő, és így T _exp kisebb lesz t-nél és F_exp nagyobb lesz f₀-nál. Ezek az általános szabályok, de a konkrét értékek már attól függenek, hogy mekkora az idő dimenziójú Γ konstans. Legyen például egyenlő az univerzum korával, vagyis Γ = t₀. Ekkor:

Hasonlítsuk össze a Γ paraméter választásából adódó időskálát a Föld forgási sebességére alapozott idő hosszúságával! Csillagászati megfontolások szerint korábban a Föld gyorsabban forgott tengelye körül, úgy 600 millió évvel ezelőtt egy fordulat ideje 21 óra lehetett, vagyis azóta a lassulás már 14,3 százalékos. Ha elképzelünk a Földön egy 600 millió évvel ezelőtti civilizációt, akik szintén a Föld forgására alapozták az egy másodpercet, az akkor 14,3 százalékkal rövidebb lehetett, mint a mai.  Mekkora viszont a különbség ennyi idő alatt, ha a Γ = t₀ egyenlőségből adódó időlassulást fogadjuk el?  Eszerint az akkori másodperc 4,45 %-kal lenne rövidebb a mainál, vagyis a csökkenés mértéke mintegy háromszor kisebb, mint ami a Föld forgássebességének változásából számítható. Nagyobb Γ választással hozzá lehetne igazítani a számított értéket a Föld forgás idejének rövidüléséhez, de ez nem indokolt, mert nem az exponenciális elv határozza meg a Föld forgási sebességének lassulását, hanem az ár-apály jelenség „lopja” el a forgási energia egy részét, azáltal hogy a mozgási energiát fokozatosan hőenergiává konvertálja.

Nézzük meg, hogy találhatunk-e valamilyen módszert Γ meghatározására! Először is meg kell vizsgálni, hogyan befolyásolja a fizika törvényeit, ha rövidebb a másodperc hossza és nagyobb a frekvenciája a fizikai folyamatoknak? Induljunk ki abból, hogy ettől a fizika alaptörvényei nem változnak meg! Képzeljünk el ismét egy civilizációt valamikor a messzi múltban, mondjuk 600 millió évvel korábban, de akár messzebb is mehetünk. Ami megváltozott, az a mi időskálánkhoz viszonyított frekvencia. Ha az akkori civilizáció ugyanolyan elveket követett mi, és például a Cézium atom sugárzásának szintén 9 192 631 770 számú periódusához kötötte az egy másodperc hosszát, akkor az egyes fizikai konstansokra ugyanakkora számértéket kapott. Valójában ezt nevezi a modern fizika mérték (gauge) invarianciának. Ehhez két dolognak kel teljesülni: azonos legyen az energia és a fénysebesség! A fénysebesség akkor lehet változatlan, ha ugyanolyan mértékben csökken a távolság is, mint az időegység, vagyis:

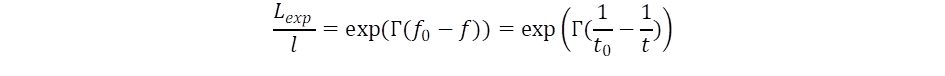
Itt L_exp a méterrúd csökkenése a nálunk meghatározott    Ɩ  hosszúsághoz képest. Az energia korszak függetlensége (invarianciája) azt jelenti, hogy a fény h·f energia kvantuma is azonos marad. Ez viszont az ottani nagyobb frekvencia miatt akkor teljesül, ha a h Planck állandó ugyanannyiszor volt kisebb a múltban, mint a távolság és az idő. Viszont az energia és c változatlansága miatt az mc², vagyis a tömeg, is ugyanakkora volt, mint a mai univerzumban. A gravitációs energia GMm/R értéke akkor marad változatlan, ha a számlálóban G és a nevezőben az R távolság azonos mértékben változik, vagyis a G általános gravitációs állandó is kisebb volt a korábbi univerzumban, ha mai korunk idő és hossz egységében számolunk. Az elektromosság Coulomb energiája Q₁·Q₂/R, akkor marad állandó, ha a töltés négyzete együtt változik a távolsággal. Amikor azt mondjuk, hogy h, G és az elektromos töltés kisebb volt, az abból fakad, hogy az általunk megszokott egységrendszerben fejezzük ki ezek értékét. Viszont az a korai civilizáció, amelyik hasonló elvek alapján definiálja az időt, a távolságot és a tömeget, mint mi (vagyis például 1 méter egyenlő a ⁸⁶Kr atom által kibocsátott sugárzás 1 650 763,73 periódus hosszával), az a fent említett fizikai állandókra a miénkkel egyező értékeket fog találni.

Megfigyelhető-e az időskála változása?

Ezek után fel kell vetni a kérdést, hogy az időegység csökkenése és a távolság rövidülése megfigyelhető-e csillagászatilag? A távolságcsökkenés elvben igen, ha meg tudjuk határozni a távoli galaxisok kiterjedését és bennük a csillagok távolságát. Korábbi példánk szerint 600 millió fényév távolságban a méretcsökkenés 4,45 százalékos, amennyiben az idő Γ skála paramétere t₀. Alkalmas lehet-e a skálaparaméter meghatározására a galaxisok méretének statisztikai elemzése? A problémát az jelenti, hogy ekkora távolságból csak a szupernova robbanás fénye látható és nem az egész galaxis. Közelebbi galaxisok esetén már meghatározható a méretük, de nem tudok róla, hogy sort került-e egyáltalán olyan csillagászati analízisre, amikor a távolság függvényében vizsgálták a kérdést. Talán a fény hullámhosszának analízise segíthetne? A vöröseltolódás a 600 millió fényévnyire levő galaxisoknál a Hubble törvényből számolva 4,35 százalékos, ez nagyon közel van a transzformációs szabályból adódó értékhez. (A különbség kis értéke abból ered, hogy kis tartományon belül az exponenciális függvény közel lineáris.) Nézzük először azt a mechanizmust, ami a távolodó objektumok esetén vöröseltolódást hoz létre a fotonok abszorpciója során. Bár a kibocsájtott és elnyelt fotonok energiája azonos, mégis létrejön az eltolódás, mert az abszorbeáló elektron csak az energia egy részéhez jut hozzá, a teljes energiát a teljes objektum veszi át. A távolodó objektum esetén a hullámhossz megnövekszik, a frekvencia kisebb lesz, és ez a frekvencia határozza meg az abszorpció pillanatában a rezonancia feltételét. Az energiából a rezonanciafrekvenciának megfelelő rész jut az abszorbeáló elektronnak, a fennmaradó rész a molekula, illetve az objektum többi részén oszlik el. A lényeg, hogy van egy valóságos fizikai mozgás a kölcsönhatás mögött. Vajon tekinthetjük-e az idő transzformációját is valóságos mozgásnak? Ez ellen szól, hogy az időskála lassulása miatt frekvencia növekedne, és nem csökkenne, ami ugyan még nem cáfolat, mert az ellentétes folyamatok egymás mellett is futhatnak, de igazolásnak sem tekinthető. Ezért jobb inkább a mozgási frekvenciák változása helyett a mozgási sebességnek az univerzum különböző korszakaiban eltérő skálázásáról beszélni.

Nézzük meg a t = 1 s tartományt is, akkor az exponenciális függvény kitevője  ̶ Γ lesz, vagyis a 13,78 milliárd évvel visszalépve exp(Γ) mértékben gyorsabb lehetett a karakterisztikus frekvencia. A standard kozmológia az univerzum történetét az 5,391·10^-44 Planck időig vetíti vissza, és ezzel fordított arányban növekszik a karakterisztikus frekvencia, amíg elérjük az egy másodpercet. Az exponens kitevője  ̶ 44-ről nullára változik, amikor az egy másodperchez érünk, innen tovább haladva jelen korunkig további 17-et változik a kitevő. A kitevők aránya mutatja, hogy az első másodperc alatt valóban sokkal több minden történt, mint az utána következő 13,78 milliárd év alatt.  Ha viszont a lineáris időnek megfelelő egy másodperc helyett az annál jóval rövidebb T_exp = exp(1  ̶ Γ) értéket vesszük alapul, ebben a sokkal rövidebb időegységben már kiegyenlítődik az eseménysűrűség az első másodperc és napjaink között.

A jelenlegi kozmológiai modell szerint az igazán nagy különbség az egy másodpercnél jóval rövidebb időzónában alakult ki. Az univerzumnak ebben a korai szakaszában elképzelhetetlenül magas volt a hőmérséklet és nagy az anyagsűrűség. Ennek következményeit nem korrigálja az időskála megváltozása, csak tompítja az események ütemét. Minden korszakban olyan fizikai folyamatot kell választani az idő és távolság egység számára, amely tükrözi az anyag aktuális mozgásait. Ha már kialakultak az atomok (380 ezer évvel az ősrobbanás után), a kibocsátott sugárzás frekvenciája (ez a mikrohullámú háttér sugárzás) lehet az időegység alapja, előtte pedig a szubatomi részecskék átalakulási sebességéből lehet kiindulni. Óvatosságra int azonban, hogy ebben a korai szakaszban a kozmológia elmélete meglehetősen spekulatív.

A mai kozmológia megtorpan a Planck időnél és arra sincs válasza, hogy mi volt az ősrobbanás előtt. Ha nem létezett univerzumunk, akkor az idő fogalma is homályba vész. Az exponenciális idő transzformáció ebben is segít, mert az exponenciális időskála nem mehet el nulláig, ahol az időtranszformáció szabálya szerint végtelen nagy lenne a karakterisztikus frekvencia. Nincs ezért kezdő pillanat, nem kell arról beszélni, hogyan lett a semmiből valami.  Nem az univerzum keletkezéséről kell beszélni, hanem korszakokról és átalakulásokról kell szólnia az elméletnek. Ez az exponenciális időfelfogás talán legfontosabb tanulsága.

Időtranszformáció és kvantummechanika

Vessük még fel azt a kérdést is, hogy az idő transzformációs szabálya mögött milyen fizikai törvény húzódhat meg.  Induljunk ki az energia kvantummechanikai operátorából, amit a  differenciálhányados ad meg. Ez az operátor invariáns az időtranszformációval szemben, mert az idő csökkenését kiegyenlíti a Planck-állandó csökkenése. A kvantummechanika változásalapú szemléletmód, ahol a változásból indulva jutunk el az állandósághoz. Először felírjuk operátorait, amellyel rákérdezünk a változásra: mi változik meg, majd megoldjuk az operátor sajátérték egyenletét. Ebben a sajátérték adja meg az állandóságot, a sajátfüggvény pedig leírja a mozgás tér- és időbeliségét.

A kvantummechanika az energiát az idő szerinti változással köti össze, a viszony azonban megfordítható: feltehető az a kérdés is, hogyan függ az idő az energiaváltozástól, azaz a 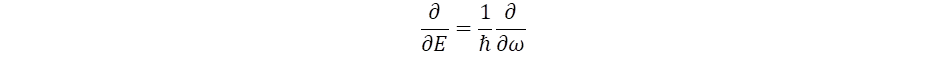    differenciálhányadostól, ahol felhasználtuk az E = h·f  = ħω Planck-törvényt is, melyben ω = 2πf a körfrekvencia. Ez alapján vezethetjük be az idő operátorát a frekvencia szerinti differenciálhányadossal definiálva:

Itt a kvantummechanikai konvencióval szemben nem szerepel az „i” imaginárius egység. Ennek oka, hogy a kvantummechanikában követelmény a normálhatóság, vagyis amikor véges értéket vesz fel az állapotfüggvény négyzetének teljes térre képzett integrálja. Ez a feltétel akkor teljesül, ha imaginárius a differenciál operátor, mert ehhez periodikus sajátfüggvény tartozik. Erre a normálhatósági feltételre azért van szükség a kvantummechanikában, mert a tér lokalizált objektumának (például az elektronnak) stacionárius állapotát akarjuk leírni, melyben a megtalálási valószínűség egységnyi lesz. Az idő és tér azonban nem szorítható korlátok közé, ezért ez a megszorítás szükségtelen, sőt ellentmondáshoz vezet. Általános elv, hogy a vizsgált jelenséghez kell alkalmas matematikai eszközt választani, nem pedig a matematikai módszerhez kell igazítani a jelenséget! A fizikai elméletekhez nem akkor vagyunk hűek, ha minden határon túl alkalmazzuk szabályrendszerét, hanem amikor kijelöljük az érvényességi kereteket.

Bár az időoperátor bevezetése kvantummechanikai analógián keresztül körülményesnek tűnhet, de komoly előnye van az eljárásnak, mert megvilágítja a kapcsolatot az energia és az idő között. Matematikailag könnyű eljutni ugyanide, ha abból indulunk ki, hogy t = 1/f, mert ebből már adódik, hogy az időt operátorként definiálva      alakú differenciális művelethez jutunk. Az időoperátor szerkezetéből következik, hogy annak sajátértéke a Γ skálafaktor, sajátfüggvénye pedig az exponenciális időtranszformáció, hiszen

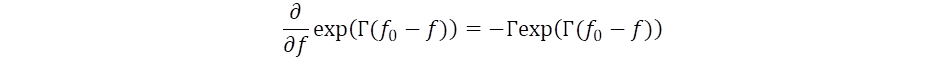
Hasonló módon értelmezhetjük a távolság operátorát, melynek sajátfüggvénye a hosszúság mértékének exponenciális csökkenését írja le, amikor a múlt felé haladunk. Az Ɩ = ct = c/f összefüggésnek megfelelően adhatjuk meg a távolság operátorát:

Az időoperátorral való arányosságból következik, hogy azonosak a transzformációs tulajdonságok is.

Konklúzió

A nemlineáris extrapoláció kozmológiai távlatait vizsgáltuk meg. Ennek során megállapíthattuk, hogy az idő- és térfüggés exponenciális skálája olyan kozmológiai szemléletmódot hoz létre, amely megalapozott fizikai elvekre támaszkodik, és elkerüli az univerzum létrejöttének problematikáját. Nem teljesíti azonban a bizonyíthatósági (cáfolhatósági) kritériumot, minthogy nincs olyan konkrét csillagászati megfigyelés, ami a szemléletmód helyességét igazolná, vagy cáfolná.