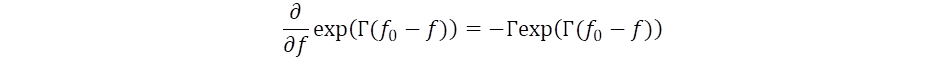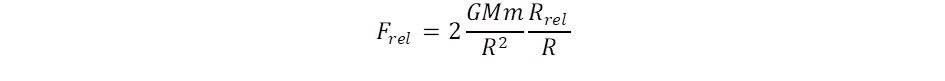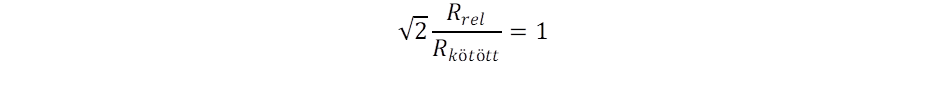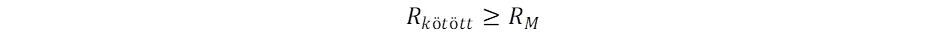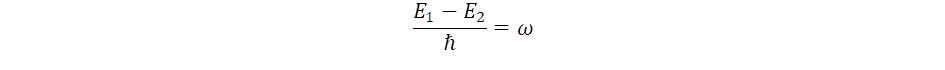Az Univerzum szerkezetének megformálója: a gravitáció és antigravitáció
Absztrakt
A tér, az idő és az anyag elválaszthatatlan egységet alkot. Elindulhatunk a tér lokális forgásaiból, amely megalkotja a mikroszkopikus részecskék világát, a négy alapvető kölcsönhatás ebből felépíti a makroszkopikus objektumokat, melyek mozgásai visszahatnak a tér szerkezetére. A gravitáció a tömeg hatása önmagára a tér szerkezetének megváltoztatása által. Ennek két formája van: lokálisan vonzás az elliptikus geometriájú galaxisokban, illetve univerzális taszítás a mindent magában foglaló hiperbolikus térben. Ehhez a fizikai világképhez az einsteini térszemlélet és a kvantumfizikai mezőelméleti felfogás összekapcsolásával juthatunk el, felhasználva a speciális relativitáselmélet transzformációs szabályait.
Bevezetés: A gravitáció Newton- és Einstein-egyenlete
Minden törvény akkor válik teljessé, ha kijelöljük érvényességi hatókörét. Ez érvényes a gravitáció törvényeire is. Newton gravitációs törvényéről először a Merkur perihéliumának vizsgálata mutatta ki, hogy korrekcióra szorul. Einstein korszakalkotó gondolata volt, hogy két tömeggel rendelkező objektum között a vonzóerőt a téridő szerkezetének görbületére vezette vissza. A testek körül a tömeg megváltoztatja a teret, és a megszokott eukleidészi egyenes koordináták helyett görbe vonalak jelölik ki a mozgás útját. Newton törvénye szerint, ha nem hat külső erő a testre, akkor megtartja egyenes vonalú, egyenletes sebességű mozgását, ez a tehetetlenség megnyilvánulása. Az einsteini képben a gravitációs erőt a görbült koordinátákhoz való igazodás helyettesíti. Korszakalkotó gondolat! Ezt a gondolatot kellet matematikai formába önteni. Newton gravitációs egyenlete háromdimenziós vektorok – a gyorsulás és erő – között adta meg a kapcsolatot. Ezt kellett a speciális relativitáselmélet szabályai szerint négydimenziós téridő koordinátákra átírni, figyelembe véve egyrészt a mozgási energia relativisztikus összegzési szabályát, amit a kovariancia elv a nyugalmi energiával kapcsol össze, valamint egy olyan tenzort, amely leírja a görbült téridő szerkezetét, ez a 4*4 dimenziós metrikus tenzor. Newton a gyorsulási vektort, ami a pálya térkoordinátáinak idő szerint második differenciálhányadosa, az erő vektorral kötötte össze. Einstein egyenlete tovább lép a három dimenziós gyorsulástól a négydimenziós téridő koordináták között képzett differenciálhányadosokig, melyekben megjelenik a metrikus tenzor is. Az erőn alapuló kapcsolat helyébe az energia és lendület tenzora lép, melyek felírásához eleve szükség van a metrikus tenzor ismeretére.. Ettől válik az egyenlet kezelése rendkívül nehézzé, mert eleve ismernünk kellene a metrikát, hogy hozzá kezdjünk az egyenlet megoldásához. Emiatt csak kivételes esetben van mód, hogy megoldást találjunk. Erre adott példát Schwartzschild, amikor a feladatot kéttest problémára egyszerűsítette és a gömb alakú Nap és a körülötte keringő szintén gömbalakú bolygó kapcsolatát vizsgálta. A számítások kiegészítették az eredeti Newton törvényt egy korrekciós erővel, amely szemben az 1/R2 távolságfüggéssel már 1/R3 szerint változik. Ez a relativisztikus korrekció azonban közvetlenül is származtatható az Einstein egyenletből való kiindulás nélkül. Ennek oka, hogy a Nap körül keringő bolygó mozgási energiája megnöveli a bolygó tömegét, ez felel meg az energia és tömeg közötti E = mc2 ekvivalencia elvnek, hiszen az energia együtt tartalmazza a nyugalmi energiát és a mozgási energiát, a megnövelt tömeg pedig – az Eötvös Loránd által bizonyított ekvivalencia törvény szerint – egyúttal nagyobb gravitációs erőt hoz létre. Ennek mértékét a gravitációs potenciális energia (GMm/R) aránya adja a bolygó mc2 nyugalmi energiájához képest1.
[1 A speciális relativitáselmélet kovariancia törvénye szerint a mozgási energia pc alakja (itt p a lendület) négyzetesen adódik össze a nyugalmi energiához:

Itt a közelítés annak az esetnek felel meg, amikor a mozgási energia sokkal kisebb a nyugalmi energiánál. Egyenletes sebességű mozgásnál a tömegnövekedés csak látszólagos, mert az inerciarendszer sebessége tetszőlegesen választható. Viszont a nem inerciális keringő mozgás esetén már valódi tömegnövekedésről beszélhetünk, ahol is a potenciális energia a mozgási energia kétszerese (lásd viriál tétel), vagyis a tömegnövekedés m – m0 = GMm/2Rc2 lesz. A mozgási energiát pedig keringés esetében az impulzusnyomaték négyzetével lehet megadni, ez jelenik meg a Schwartzschild által megadott kifejezésben. Érdemes még összevetni ezt a gravitációs tömegnövekedést az atommagok tömegdeficitjével, ahol kisebb a tömeg, mint ami a nukleonok (protonok és neutronok) számából következne. Itt azért alakul ki tömegdeficit, mert a nukleonok az erős kölcsönhatás révén kapcsolódnak össze, melynek során a fúziós reakcióban gammasugarak kibocsátására kerül sor, ami a visszamaradó energiát lecsökkenti. Gravitációs kötött állapot létrejöttekor, például amikor egy bolygó a Nap körül befogásra kerül, nincs kisugárzott energia.]
Einstein gravitációs egyenletének érvényességi köre
Térjünk most rá az értelmezési keretekre. Ebben válasszuk szét az alapgondolatot és a belőle származó gravitációs egyenletet. Két körülményt kell megvizsgálni!
- Mekkora az a távolság, amelyen belül igazoltnak vehető a törvény érvényessége
- Mekkora az a téridő görbület, amelynél ellenőrizhetjük a törvényt
A Naprendszeren belül rengeteg csillagászati adat támasztja alá a gravitációs egyenlet helyességét, ezek az adatok akkora távolságra vonatkoznak, melyek a fényév kevesebb, mint egy százalékát teszik ki. De mi van azon túl? Ha a Tejút határáig elmegyünk, akkor százezer fényévnyi távolságról beszélünk, azaz legalább tíz milliószor nagyobb távolságról van szó! Biztosak lehetünk benne, hogy Einstein és Newton gravitációs egyenletei ekkora távolságban is helyes eredményre vezetnek? Az óvatosság távolról sem alaptalan! A Naprendszerben keringő bolygók és égitestek sebessége jól követik a Kepler-Newton törvényt, a távoli bolygók keringési sebessége lassul az u2R = GM törvénynek megfelelően (Itt M a Nap tömege, G az általános gravitációs állandó), de a Tejút centrumtól távolabb keringő csillagok pályasebessége nem csökken a távolsággal, ami a 10-től 50 ezer fényévig 220-240 km/s körül van. Ráadásul a galaxis teljes tömegének vonzereje kevés ahhoz, hogy a nagy sebességgel keringő csillagokat pályán tartsa, azaz ne lépjenek ki a galaxisból.
Mit lehet tenni akkor, ha kiderül, hogy bizonyos esetekben a tapasztalati tények ellentmondanak valamilyen elméletnek? Két módon járhatunk el:
- Feltételezhetünk valamilyen láthatatlan, megfigyelhetetlen anyagot, vagy kölcsönhatást, amelynek hatása okozza az eltérést. Erre már korábban is volt példa, amikor Le Verrier francia matematikus azzal magyarázta a Merkur bolygó perihéliumának eltolódását, hogy létezhet egy megfigyelhetetlen sötét bolygó, a Vulkán, amely perturbálja a Merkur bolygó pályáját. Hasonló szerepet játszott az elektromágneses kölcsönhatás elméletében az éter fogalma is.
- Megadhatjuk a korábbi elmélet hatókörét, és kiegészíthetjük a korábbi elméletet abban a tartományban, ahol már eltérést tapasztalunk. Erre szép példa Einstein általános relativitáselmélete, melyből egy a bolygók keringését befolyásoló korrekciót adódik ki. Ez a korrekció akkor válik jelentőssé, ha erős gravitációs csatolás alakul ki a központi égitest és a bolygó között, a naprendszerben ez leginkább a Merkurra vonatkozik. Amint arra rámutattunk, ehhez a korrekcióhoz a Newton elmélet keretei között is eljuthatunk, ha támaszkodunk egyrészt az energia és tömeg ekvivalenciájára, másrészt az Eötvös-féle ekvivalencia elvre a tehetetlen és gravitáló tömeg között.
Honnan származik a sötét anyag koncepciója?
Nagy csillagászati távolságok esetén, vagyis akkora méretben, ami a Tejútra jellemző, eltérés lép fel a csillagászati tapasztalat és Einstein illetve Newton egyenlete között. Ebben a tartományban a relativisztikus és a klasszikus gravitációs elmélet lényegében azonos. Ne feledjük, hogy hatalmas a különbség a Naprendszer bolygóinak pályája (kb. egy ezred fényév) és a Tejút mérete (100 ezer fényév) között! A jelenleg széles körben elfogadott kozmológiai elmélet az első utat választja, amikor feltételezi, hogy létezik egy láthatatlan gravitáló anyag, a sötét anyag, amelynek gravitációs hatása tartja egyben galaxisunkat. Ennek az anyagnak mennyiségét mintegy hatszorosára teszik a látható anyaghoz képest.
Ennek a sötét anyagnak a feltételezése már korábban megtörtént Zwicky svájci-amerikai csillagász által, aki részletesen vizsgálta a Coma szuperhalmaz dinamikáját 1933-ban. Ez a tőlünk 320 millió fényévre levő gömbhalmaz 10 millió fényév átmérőjű és mintegy 3000 galaxis építi fel, és a galaxisok közötti tipikus távolság 1 millió fényév. Ennek az adatnak később, még nagy jelentősége lesz! A Doppler effektus alapján a külső galaxisok sebessége a centrumhoz képest 1000 km/s körül van. Zwicky a viriál-elvből indult ki és összevetette, hogy mekkora az arány a halmaz teljes mozgási és gravitációs potenciális energiája között. Az elmélet szerint a potenciális energia fele egyezik a mozgási energiával, viszont Zwicky számításai arra vezettek, hogy 450-szer nagyobb tömegre lenne szükség, hogy ez a feltétel teljesüljön.
A sötét anyag hipotézise további alátámasztást nyert a gravitációs lencsehatás megfigyelésével. Az egyes galaxisok képe megsokszorozódik amiatt, hogy a tér görbült szerkezetéhez igazodó fény lencse módjára viselkedik. Ez szintén az einsteini koncepcióból adódik, viszont a jelenség nagyobb intenzitással jelentkezik, mint amit a csillagok fényessége alapján számított tömeg indokolna. Ebből adódik a következtetés, hogy itt is döntően a sötét anyag alakítja ki a tér szerkezetét.
A sötét anyag koncepció ellentmondásai
Tehát sok minden szól a sötét anyag létezése mellett. De csak látszólag, mert itt is igaz, hogy az ördög a részletekben bújik meg! Az első kérdés, ami felvetődik, hogy miből is épülhet fel ez a sötét anyag? A látható anyag, mint jól tudjuk, az atommagokból, vagyis a neutronok és protonok sokaságától származik. Létezne talán valamilyen elektromágnesesen megfigyelhetetlen – de gravitációs hatással rendelkező – részecske is (WIMP2), vagy van valamilyen megfoghatatlan kontinuum, valamiféle éter? Spekulációk sokaságával találkozhatunk a szakmai irodalomban is. Több mint egy tucat csillagászati expedíciót indítottak útnak, hogy a sötét anyag nyomára bukkanjanak, de teljes lett a kudarc. Baj van a számokkal is, a Coma klaszter esetén 450, a Tejút esetén 6-szoros, a gravitációs lencsehatás esetén 3-szoros az arány, amit a sötét anyag mennyiségére kaptak. Baj van a sötét anyag térbeli eloszlásával is, a Coma halmazban azonos a sötét és látható anyag eloszlása, viszont a Tejútban csak úgy lehet értelmezni a csillagok egyenletes keringési sebességét, ha a sötét anyag a galaxis perifériáján helyezkedik el.
[3 WIMP azaz „weakly interactive massive paticle”, azaz gyengén kölcsönható tömeggel rendelkező részecske.]
A gravitációs elmélet kiterjesztéséhez Hubble tágulási törvényén át vezet az út!
Induljunk el hát a másik úton, nézzük meg, hogy hol érvényes a jelenlegi gravitációs elmélet és hol kell azt kiegészíteni? A galaxisok távolodnak tőlünk. Hubble amerikai csillagász állapította meg, hogy minél távolabb van tőlünk egy galaxis, annál nagyobb a vöröseltolódás, azaz annál nagyobb a v = H·D távolodási sebesség, ahol D jelöli a távolságot és H a Hubble konstans. Ezt a távolodást értelmezzük úgy, hogy a tér tágul, és emiatt figyeljük meg, a galaxisok vöröseltolódását. Ez a törvény valójában gyorsulási törvény, hiszen sebességváltozásról van szó. A relativitáselmélet alapelve, hogy minden kölcsönhatás fénysebességgel terjed, ezért a D távolságból érkező információ t = D/c idő alatt jut el hozzánk, ez a retardációs idő. Ez alapján a tágulási gyorsulás:
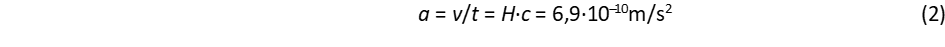
Ez összevetve a földi gravitációs gyorsulással (g = 9,81 m/s2) tíz nagyságrend a különbség, amiért nem figyelhető meg földi körülmények között, viszont elvi szempontból mégis jelentős, mert emiatt a táguló univerzum nem tekinthető inercia rendszernek. A relativitáselmélet Lorentz kontrakciós szabálya szerint a v sebességű mozgás irányában, vagyis a tér tágulásánál sugárirányban, a távolság rövidülni fog:
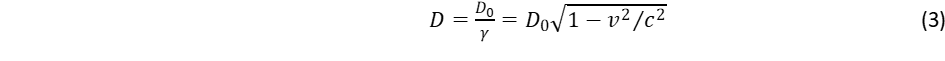
A kör kerülete, illetve a gömb felszíne merőleges a sugárra, ezért a táguló mozgás nem változtatja meg a kerületet, illetve a felületet, vagyis a kerület és átmérő aránya többé nem π lesz, hanem annál nagyobb. Vagyis kilépünk az eukleidészi geometria axiómarendszeréből, még pedig a Bolyai és Lobacsevszkij által leírt hiperbolikus geometria felé. Ez pont fordítottja az elliptikus geometriának, amely a Riemann által kiterjesztett geometriai koncepció másik változata Ennek különös jelentősége van az einsteini gravitációs koncepcióban, amely a gravitációt a térgeometria görbületével értelmezi. Ugyanakkor az einsteini vízió csak elliptikus geometriáról beszél. Ennek oka, hogy Einstein a gravitációs vonzást akarta értelmezni, amikor a testek egymás felé mozdulnak a gravitációs vonzás miatt, ahogyan a párhuzamos egyenesek is egymásfelé hajlanak. Ez pont fordítottja a hiperbolikus geometriának, ahol a párhuzamos egyenesek széttartanak. Az einsteini koncepciót kiterjesztve az intergalaktikus térre, azt kapjuk, hogy nagy távolságban taszítják egymást a galaxisok, vagyis a galaxisok gyorsuló szétterjedését a galaxisok között fellépő antigravitációs taszítás okozza. Ezzel eljutottunk a kozmológia egyik nagy rejtélyéhez, amely az ismeretlen eredetű sötét energiával értelmezi a galaxisok gyorsuló szétrepülését, vagyis az univerzum tágulását. A sötét energia tehát nem más, mint az univerzum többszáz milliárd galaxisának antigravitációs energiája. Az ősrobbanás utáni szétáradás teremti meg azt a hiperbolikus geometriát, amely a későbbiekben – és a jelenben is – gyorsulva tarja fenn az univerzum tágulását. Másszóval a Big Bang kezdeti robbanása teremti meg a későbbi gyorsuló tágulás előfeltételét.
Térjünk vissza a gravitációs vonzás eredetéhez!
A táguló univerzum magyarázatának legfontosabb megállapítása, hogy eleve létezik egy olyan térmozgás, amely a tér hiperbolikus geometriájához vezet. Térjünk most rá Einstein hipotézisére, aki a tömeg hatására létrejövő elliptikus geometriáról beszél. De hogyan görbíti meg a tömeg a teret, hogyan lesz a kör kerületének aránya az átmérőhöz viszonyítva kisebb, mint π értéke? Forduljunk ismét a Lorentz kontrakció szabályához, hogy megtaláljuk a választ! Körmozgás esetén csak a kerület hossza csökken, a rá merőleges sugár változatlan marad, és így elliptikus geometriához jutunk, amelyben tényleg kisebb a kerület és az átmérő aránya π értékénél. A Kepler törvényben az m tömegű bolygó az M tömegű Nap körül az u2R = GM szabály szerint kering, ha az m tömeg kicsi M-hez képest. Tehát a keringő test tömegétől független a sebesség, legalább is addig, amíg a mozgó tömeg kicsi a keringést előidéző tömeghez képest. Indokolt ezért a feltételezés, hogy a nulla tömegű tér is foroghat a tömeg körül! Innen származik a hipotézis, hogy a tömeg megforgatja maga körül a teret a Kepler szabálynak megfelelően. A tömeg teret forgató hatása fejezi ki azt a felfogást, hogy valójában a tér és az anyag egységet alkot, a kettő kapcsolata kölcsönös. A Föld körüli pályán levő űrhajóból kitett test együtt kering az űrhajóval. Fogjuk úgy fel a keringő mozgást, hogy valójában a forgó tér viszi magával a testeket. A tér mozgásának viszont nincs kitüntetett forgástengelye, a gömbszimmetrikus mozgás megköveteli, hogy a tér azonos módon forogjon két tengely körül. Ennek megértésében segít a kvantummechanika szemléletmódja, amely nem a tér és idő koordinátákkal írja le a mozgási pályát, hanem mozgási állapotokról beszél a tér és a valószínűség dimenziójában. A gömbszimmetrikus mozgásállapotban nincs a tér forgásának kitüntetett tengelyiránya, minden forgástengely egyformán valószínű. Evvel szemben a klasszikus pályafelfogás szerint a tömeggel rendelkező objektumok keringése nem lehet gömbszimmetrikus, hanem a lehetséges tengelyirányok közül valamelyik kiválasztásra kerül, és ellipszis váltja fel a körpályát, függően a perdület irányától és nagyságától. Az Einstein által megalkotott modellben a gravitációt a tér görbületi struktúrája idézi elő, ezt egészítjük ki avval a kérdéssel: hogyan képes a tömeg görbületet létre hozni a térben?
Amikor megalkotunk egy modellt, felvetődik a kérdés: mi annak feltétele, hogy a modell helyes legyen? Ehhez két követelménynek kell teljesülni: legyen összhangban a megfigyelésekkel, és ne legyenek benne egymásnak ellentmondó premisszák.
Az eddigiekben kétféle térmozgásról volt szó, most kapcsoljuk össze a kettőt! Mindkettő a tömeg hatása: az egyik a tágulás, a másik a gömbforgás, az egyik galaktikus távolságban érvényesül, a másik kisebb távolságban, például a Naprendszeren belül, az egyik antigravitációs taszítást, a másik gravitációs vonzást hoz létre a tömeggel rendelkező testek között. A kérdés természetesen felmerül, hol van az elválasztó határ?
Mezőelméleti kitekintés
Az elméleti fizika százév óta megoldatlan kérdése, hogy nem sikerült kvantumos gravitációs elméletet kidolgozni annak mintájára, ahogy az elektrodinamika kvantummező elmélete, a QED (Quantum Electro-Dynamics) működik. Atomokban és molekulákban az elektron állapotok közötti ugrásokat elektromágneses sugárzás kibocsátása és elnyelése valósítja meg, és ez a sugárzás fotonok által közvetített kvantumokban megy végbe. A mezőelmélet azonban nem csak az ugrásokat írja le fotonokkal, hanem a kölcsönhatási erőt is fotonokkal építi fel, ezek a kibocsátott és elnyelt, de nem látható virtuális fotonok. Vajon miért vallott kudarcot a sok erőfeszítés, hogy hasonló kvantumos folyamatot találjunk a gravitációs kölcsönhatás számára is? Ennek oka, hogy összhangra van szükség a kölcsönhatásról szerezhető információ és a választott elmélet struktúrája között. Rossz úton indulunk el, ha valamilyen elméleti előfeltételt akarunk ráerőltetni egy fizikai folyamatra. Konkréten szólva: szemben a molekulaképződés és magfúzió folyamataival, a gravitációs kötött állapot létrejötte nem jár együtt megfigyelhető sugárzással, e-nélkül pedig nem kaphatunk kvantumos információt. Valamilyen közvetítő folyamatra viszont szükség van, hogy a távoli objektumok hatással legyenek egymásra, és ez a hatás – a relativitáselmélet játékszabályai szerint – fénysebességű terjedéssel valósuljon meg. Ezt a közvetítő mechanizmust a gömbszimmetrikus forgásba hozott tér alkotja meg, ahol a forgás egyidejűleg két tengely körül történik, akkora frekvenciával, amely megfelel a Kepler törvénynek. Ezt a térforgást nevezzük a továbbiakban kepleronnak, amely csak korlátozott értelemben tekinthető részecskének, mert nem sorolható be a részecskefizika spinnel rendelkező fermionjai és bozonjai közé. Ennek oka, hogy a kepleron nem rendelkezik perdülettel (spinnel) eltérően a fotonoktól. A kepleron mechanizmus tulajdonságait a fotonnal való összehasonlításon keresztül érthetjük meg. Ennek alapja, hogy a fotonokat fénysebességű forgások alkotják, míg a kepleronok forgási sebessége nem érheti el a fénysebességet, sőt a kerületi sebesség még csökken is a távolsággal az u2R = GM Kepler szabály szerint. Nem árt hangsúlyozni, hogy a forgási és a terjedési sebesség nagysága különbözik a kepleronoknál, szemben a fotonokkal, ahol a két sebeség azonos és c-vel egyenlő! A kepleronok abban már hasonlítanak a fotonokra, hogy szintén fénysebességgel terjednek, és a részecskeintenzitás az 1/R2 szabály szerint csökken. További különbség a fotonokhoz képest, hogy terjedésük során átalakulnak a Hubble-féle tágulási szabály következtében, és intergalaktikus távolságban gravitációs vonzás helyett már antigravitációs taszítást indukálnak a tömegek között. Ennek megfelelően a tömegek között fellépő erőnek is két arca van: lehet taszító vagy vonzó akárcsak az elektromos erő, de ez nem a tömeg eltérő jellegéhez (a töltés lehet negatív, vagy pozitív, szemben a mindig pozitív tömeggel), hanem a távolsághoz kapcsolódik.
A kepleronok és fotonok közötti további különbség a megfigyelhetőségben van. Fotonok esetén egyaránt beszélünk megfigyelhető és virtuális részecskékről, ugyanakkor megfigyelhető kepleron nem létezik. Kizárólag virtuális kepleronokról beszélhetünk, melyek szerepe, hogy folytonos emissziójuk és abszorpciójuk révén közvetítsék a kölcsönhatást két tömeg között. Ez a folytonosság specifikus tulajdonság, szemben a fotonok kvantumokban történő emissziójával és abszorpciójával. Az erőhatás kiváltója a lendületváltozás, ezzel a lendületváltoztató képességgel rendelkeznek a kepleronok is, bár nincs tömegük hasonlóan a fotonokhoz. A virtuális kepleronok felhőként veszik körül és kísérik a tömeget, úgy is mondhatjuk, hogy ezek a mozgó részecskék láthatatlan „küldöttei”. Ha egy másik tömeg ebbe a felhőbe kerül, a felhő belső tartományában vonzás, távoli régiójában taszítás alakul ki a kepleronok közvetítésével.
A Newton törvény reprodukálása kepleronokkal
Nézzük meg, hogyan jutunk el a Newton törvényhez abban a modellben, ahol a tér kepleron forgása hozza létre a görbült geometriát! A görbület a gömb felületének és sugarának viszonyával adható meg:
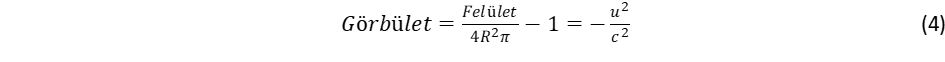
A nulla görbület felel meg az eukleidészi geometriának. A relativitáselmélet alapvető megállapítása szerint az m tömeg nyugalmi energiáját az E = mc2 tömeg-energia ekvivalencia elv fejezi ki. A részecskék fénysebességű forgás modelljében ezt az energiát a forgás mozgási energiájaként értelmezhetjük. Az u = c esetben viszont a görbület a ̶1 értéket veszi fel, vagyis a részecske nulla felületű egydimenziós objektum, amelynek azonban van egy véges r = c/ω sugara, ahol ω a fénysebességű forgás körfrekvenciája. A fénysebességű forgás mc2 mozgási energiáját az egységnyi görbülethez tartozó ̶ mc2 potenciális energia egyenlíti ki. Így jutunk el ahhoz a felfogáshoz, hogy a térgörbület és mc2 szorzata az m tömeg görbült térben felvett potenciális energiája! A gravitációt pedig szemléletesen úgy képzelhetjük el, hogy a gravitációt létrehozó M tömegű részecske r sugarú „lapátja” felkeveri a környező teret, megalkotva azt a görbületi struktúrát, amit kepleronnak nevezünk. Ha most egy másik m tömeg ebbe a „hullámtérbe” került, az a görbülettel arányos potenciális energiára tesz szert:
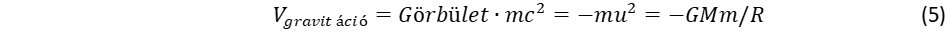
Itt az u2R = GM Kepler törvényt használtuk fel. Gondolatmenetünk megfordítja a szokásos utat, mert nem a Newton törvényből származtatjuk a Kepler szabályt, hanem fordítva, a Kepler szabály alapozza meg a Newton törvényt.
Lépjünk tovább, és származtassuk a gravitációs erőt R szerint deriválva, azaz negatív gradienst képezve:
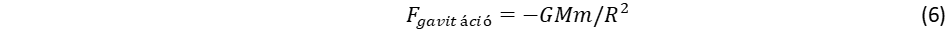
A kepleron részecske felfogásában úgy is értelmezhetjük az m tömegre ható gravitációs erőt, hogy azt az M tömeg által kibocsájtott GM/R2c2 intenzitású kepleronok hozzák létre. Látható tehát, hogy a kepleron elv tényleg elvezet a Newton törvényhez. Mint már említettük, nem csak a Newton törvény reprodukálható, hanem a relativisztikus járulék is. Ehhez csupán két ekvivalencia szabályra van szükség, egyrészt a tömeg és energia, másrészt a gravitáló és a tehetetlen tömeg között.
Gravitációs határtávolság
Alkalmazzuk az einsteini koncepciót, amely összeköti a gravitációt és a térgörbületet, hogy eljussunk az antigravitációs erőhöz! Ehhez a tér tágulásából eredő sugár irányú kontrakciót vesszük számításba. Induljunk ki abból a tartományból, ahol a v = H·D tágulási sebesség kicsi a fénysebességhez képest! Ekkor egy közelítő görbületi formula adható meg4:
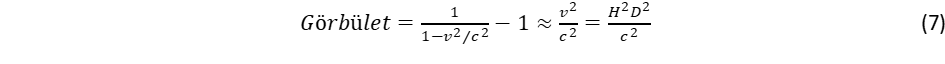
[4A pontos görbületi formulát két szöggel adhatjuk meg:
sina= u/c és sinβ = v/c
Ekkor a Lorentz kontrakció mértéke cosa, illetve cosβ, a görbületet pedig a kettő együtt adja meg:

A kibocsátási helytől távolodva a tágulási sebesség növekszik, ugyanakkor a Kepler sebesség csökken, amiért létezik egy D = R távolság, ahol a két sebesség megegyezik, és a görbület nulla lesz:

Ez a sugár kijelöl egy tértartományt, amelyben elliptikus a geometria. Ennek térfogata arányos a benne foglalt tömeggel:

Ezt a határtávolságot nevezhetjük inverziós sugárnak is, ahol a gravitáció már antigravitációba megy át. A kepleron koncepció érvényessége azon áll, vagy bukik, hogy mekkora az a határtávolság, ahol a gravitáció átmegy antigravitációba. Tejút esetén megbízható becsléssel rendelkezünk a tömeg értékére. Mivel olyan modellt állítunk fel, ahol a csillagok keringési sebességét nem a sötét anyag koncepcióra alapozzuk, ezért a szakirodalomban közölt adatokból csak a látható anyagot vesszük figyelembe: MTejút = 0,5·1042kg.
A G = 6,67·10-11m/kgs2 és H = 2,3·10̶10 1/s értékek alapján 2 millió fényév távolságot kapunk a határtávolságra. Ez az érték pontosan illeszkedik a csillagászati megfigyelésekhez! Jóval nagyobb, mint a Tejút 100 ezer fényévnyi átmérője, és közel megegyezik a legközelebbi galaxis, az Androméda 2,5 millió fényévnyi távolságával. A tipikus galaxis közi távolság 5 millió fényév, vagyis ennél nagyobb, és így a galaxisok már taszítani fogják egymást. Kivételt képeznek a Coma szuperhalmaz galaxisai, melyben a szomszédos galaxisok távolsága 1 millió fényév. Ennek azért van jelentősége, mert emiatt az egész halmaz gravitációsan összekötött csillagászati objektumnak tekinthető. Az is világossá válik, hogy miért csak 10 millió fényévnél távolabbi galaxisoknál érvényes a vöröseltolódás Hubble törvénye, ugyanis ekkora távolság szükséges ahhoz, hogy a lokális mozgások tipikus sebességét meghaladja a tágulási szabálynak megfelelő érték.
Makroszkopikus kepleronok kialakulása
De mekkora a galaxisokat egymástól eltaszító antigravitációs erő? Vizsgáljuk meg két galaxis között az antigravitációs kölcsönhatást, amikor távolságuk meghaladja az inverziós határt!
Hogy eljussunk idáig, előszőr a nukleonok gravitációs összegzési szabályait kell tisztázni. Az anyagi objektumok tehetetlen tömegének döntő részét a nukleonok adják ki, ehhez az elektronok kevesebb, mint egy ezreléket adnak hozzá. Az Eötvös-féle ekvivalenciaelv szerint, azonosan adódnak össze a tehetetlen és a gravitáló tömegek. Ez vonatkozik az atommagok tömegére is, amely kisebb, mint a benne összekötött nukleonok teljes tömege, ezt nevezzük tömegdeficitnek. Az ekvivalencia elv értelmében a tömegdeficit egyúttal gravitációs deficitet is jelent. Ennek oka, hogy a nukleonokat összekötő erős kölcsönhatás sokkal-sokkal erősebb, mint a gravitációs erő. Ez megnyilvánul a nukleonok közötti rendkívül rövid távolságában, ami 10-15 m körül van. Ezt összevetve a nukleonok 20 cm körüli inverziós sugarával, az arány több, mint 15 nagyságrend. Úgy is fogalmazhatunk, hogy az erős kölcsönhatás egybe forrasztja az egyes nukleonok által kibocsátott elemi térforgásokat, és az egyedi nukleon szintű kepleronok atommag szintű kepleronná egyesülnek. Bár az elektronok tömege kevesebb, mint egy ezrelék az atommaghoz képest, de ez is hozzájárul az atom gravitációs hatásához. Itt az összeforrasztó hatást az elektromos erő nagysága adja a gravitációs erőhöz képest. Az elektron keringési sugara 10-10 m körül van, ami 10 nagyságrenddel kisebb az inverziós sugárnál. Kondenzált fizikai fázisban is hasonló az atomi távolság, itt a szomszédos atomok által kibocsájtott elemi kepleronok olyan 1/R2 szerint csökkenő görbületi profilokat hoznak létre, ahol az átfedés tökéletes, vagyis a görbületek összeadódnak.
A szomszédos atomok Kepler forgásai tehát összeadódnak, de hogyan változik a helyzet csillagászati objektumok esetén, ahol jóval nagyobb a méret, mint az egyedi nukleonok inverziós sugara? A kérdésre választ a Newton féle gömbhéj szabály ad: ha homogén szerkezetű gömbalakzat gravitációs erejét számítjuk, akkor azonos eredményt kapunk, ha az egész tömeget a középpontba helyezzük el. Ezért beszélhetünk makroszkopikus kepleronról csillagok és bolygók esetén. Bár elemirészecske szinten a gravitáció rendkívül gyenge, csillagászati szinten már domináns erővé válik. Ezt az utat a többi kölcsönhatás kövezi ki, amikor létrejönnek a hatalmas fizikai objektumok, a csillagok és bolygók.
Tipikus méretű csillag esetén a makro kepleron inverziós sugara a (8) egyenlet alapján 1000 fényév körül van. De hogyan adódnak össze a görbületi profilok a csillagok között? A galaxisok csillagsűrűségéből adódó csillagközi távolságok kisebbek az inverziós sugárnál, ezért közöttük vonzás alakul ki, de ekkor csak a görbületi profilok széle fed át, és nincs szó homogén szerkezetű nagy sűrűségű gömbről, amiért a csillag dimenziójú makro kepleronok már nem nőnek össze, egymástól függetlenül építik fel a kölcsönhatást a galaxison belül és a galaxisok között. Ebben az értelemben beszélhetünk a kepleronok részecske modelljéről. Mindaddig, amíg a csillagok távolsága az inverziós sugárnál kisebb, még egybefüggő gravitációs tömböt alkot a galaxis, és emiatt a galaxis inverziós sugara arányosan nő a tömeggel, és jóval nagyobb lesz a makro kepleronoknál. (Itt megemlítjük, hogy az akkora csillagászati egységeknél, mint a mi Naprendszerünk, ahol a bolygó távolságok nem haladják meg a fényév századrészét sem, a távoli galaxisból érkező makro kepleronok nem befolyásolják a bolygók keringését. Számottevő antigravitációs hatást a Tejútban csak az 1000 fényévet meghaladó távolság felett várhatunk.)
Az antigravitációs erő nem csökken a távolsággal!
A részecske modell szerint az M tömegű galaktikából kibocsájtott kepleronok intenzitását a GM/R2c2 függvény írja le. Az intergalaktikus tér görbületét az egyes kepleronok által előidézett H2R2/c2 görbület és az intenzitás szorzata adja meg:
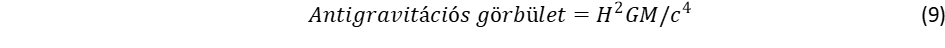
Az inverziós határnál távolabb, a távolság négyzetével arányos görbületet éppen kiegyenlíti a kepleronok számának csökkenése. Ekkor az M1 és M2 tömegű galaxisok közötti antigravitációs taszítási erő:
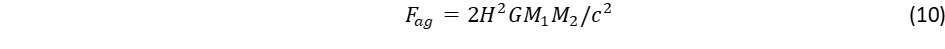
A 2-es faktor onnan származik, hogy az M1 tömeg gravitációs mezőjében M2, az M2-jében az M1- re gyakorolt hatást kell számításba venni. Ennek oka, hogy M1 jelene kapcsolódik M2 múltjához és fordítva Ml múltja M2 jelenéhez.
Az antigravitációs erő különleges tulajdonsága, hogy két galaxis között a távolságtól független a taszító erő. Ez magyarázza, hogy miért olyan nagy az univerzum táguláshoz rendelt sötét energia: ez a kozmológiai becslések szerint az univerzum teljes energiájának 65-70 százalékát teszi ki. Ennek valódi forrása ugyanis az univerzum hatalmas számú galaxispárja, ami többszáz milliárdszor többszáz milliárdot, vagyis összességében 1023 számú galaxispárt jelent.
Az a nevezetes lambda tag!
Einstein, amikor megalkotta gravitációs egyenletét, önkényesen kiegészítette egy L-val jelölt taszítási taggal, hogy magyarázza, miért nem omlik össze az univerzum, ugyanis kell valami, ami ellensúlyozza a vonzást a tömegek között. Ez a taszító kölcsönhatás mindenütt jelen van és a tér a priori görbületével arányos. Alaposabb meggondolások azonban kiderítették, hogy ez a modell nem hozhat létre sztatikusan stabil univerzumot, viszont jól használható a táguló univerzum kozmológiájában. Így aztán a jelenleg széleskörben elfogadott L-CDM kozmológiában5 a sötét energiának nevezett járulék központi szerepet játszik. A (10) egyenlrtben megadott antigravitációs erő pontosan azt a szerepet játssza el, mint Einstein elméletében a L tag, csakhogy ez nem a tér apriori szerkezeti tulajdonsága, hanem az univerzum teljes tömegének antigravitációs hatása.
[5 A CDM a sötét anyag hőmérsékletére utal (Cold Dark Matter), mert egyes hipotézisek forró, meleg illetve hideg sötét anyagról beszélnek, de a ma elfogadott nézet szerint a „hideg sötét anyag” a befutó.]
A gravitáció és a préshatás összjátéka a Tejút szerkezetében
Korábbi írásban foglalkoztunk a gömbszerű csillagászati objektumok kialakulásával. Ebben kulcsszerepet tölt be a gravitációs erő és a nyomás változása, amikor a centrum felé haladunk. Közeledve a centrumhoz az erő egyre kisebb és a centrumban már „súlytalanságról” beszélhetünk, ezzel szemben a nyomás összegezi a felületre ható erőt, amely maximális lesz a középpontban. Bár a Tejút nem gömbszerkezetű, inkább egy lapos forgó koronghoz hasonlít, amelynek spirális karjai vannak, néhány tanulság mégis átvehető. Az egyik a gravitációs erő változása, amely lecsökken a középpontban, a másik a nyomás növekedése. A lecsökkent gravitációs erő miatt a csillagok keringési sebessége a centrumban viszonylag kicsi, majd kifelé haladva növekszik, a belső szakaszban a v = ωR szabály szerint. A centrum nagy nyomására utal, hogy a belső tartományban hatalmas a csillagsűrűség, ami a központi gömb, illetve rúdalakú csoportosulásban mutatkozik meg. Ugyanez a nyomás hozza létre a hatalmas méretű fekete lyukat is a centrumban.
Haladjunk kifelé a Tejút centrumából, 5 ezer fényév körül már új jelenségre figyelhetünk fel! Ugyanis innen kifelé egészen az 50 ezer fényéves galaxishatárig a csillagok keringési sebessége alig változik, vagyis nem követi a Kepler szabálynak megfelelő csökkenést. Az eddig elmondottak alapján már gyanakodhatunk, hogy itt a távoli galaxisokból származó antigravitáció játszhat szerepet. Ennek megértéséhez képzeljük magunk elé az egész univerzumot több száz milliárd galaxisával! Válasszunk ki egy pontot valahol az univerzumban, ide fut be a sok galaxis antigravitációs taszító ereje. A kép hasonló ahhoz, ahogy a Föld középpontjában az erők kiegyenlítik egymást. Most is ez történik a galaktikus eloszlás közel homogén jellege miatt, csak itt a minden irányból érkező taszítóerő játssza el ugyan azt a szerepet, mint a Földben a centrum irányába ható gravitáció. De mi történik azokban a tértartományokban, ahol gravitációs erővel összekapcsolt csillagvonulatok vannak, és elliptikus geometria alakul ki? Itt a csillagászati alakzat felületére az antigravitációs erő nyomást gyakorol, és az egységnyi felületre jutó préselő erő mindenütt azonos lesz, legalábbis olyan mértékben, amennyire a galaxisok eloszlása homogén. Szemléletesen ezt úgy képzelhetjük el, hogy a galaxisok elliptikus szigeteit a környező hiperbolikus óceán préseli össze. Viszont eltérő lesz a préshatás, attól függően, hogy milyen a csillaghalmaz alakja és mekkora a felülete. Az összepréselt elliptikus „szigetek” tömegsűrűsége megnövekszik és így nagyobb lesz ott a tér görbülete is. Emiatt a külső préshatás pontosan azt a szerepet játssza el, amit a jelenlegi kozmológia a sötét anyagnak tulajdonít: stabilizálja a keringő csillagok pályáját és megnöveli a gravitációs lencsehatást.
Hogyan változik az egyes csillagok pályája a Tejútban az antigravitáció miatt? A külső préshatás a csillagokat ugyanúgy a centrum felé nyomja, ahogy a gravitációs erő. Kifelé haladva a Tejútban a a gravitációs vonzó erő 1/R2 szerint csökken, de erre rárakódik a külső préshatás, és végeredményben 1/R tempójú lassabb csökkenés jön létre (lásd az 1. és 2. ábrát). Az erőprofil megváltozott karakterisztikája visszaigazolja a Milgrom által felállított MOND6 modellt, de ehhez nincs szükség a newtoni dinamika megváltoztatására, mert a külső préshatás már kielégítő magyarázatot kínál.
[6 MOND = Modified Newtonian Dynamics, kidolgozója Milgrom izraeli fizikus.]
Hogyan változik meg a csillagok keringési pályája a galaxis külső tartományában, ahol domináns az antigravitációs nyomás? Az olyan felépítésű galaxisokban, mint a Tejút, amely lapos koronghoz hasonlít, az antigravitációs „súly” akkora felületre hat, amely arányos a centrumtól való távolsággal, és ezért a csillagokat pályán tartó erő épp úgy 1/R függést mutat, mint a centrifugális erő, amiből már következik, hogy a csillagok keringési sebessége közel azonos lesz a Tejút centrális tartományától eltekintve.
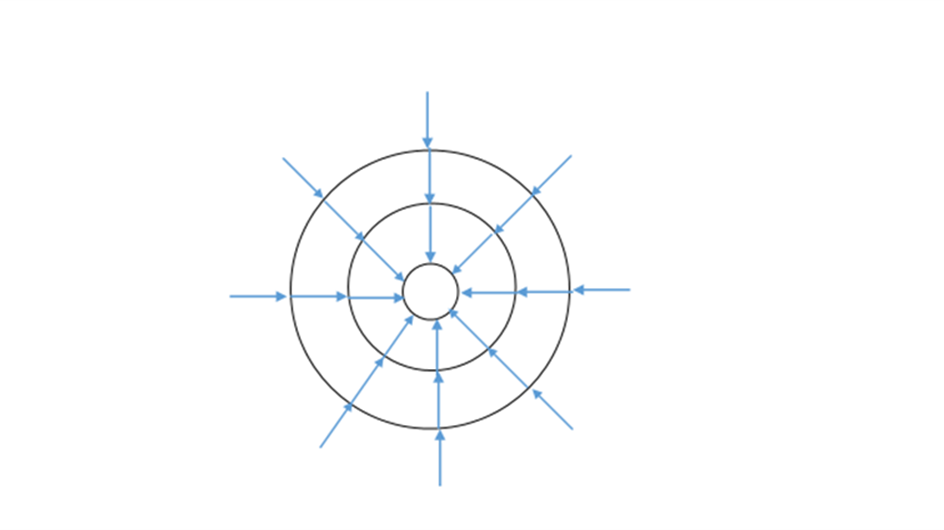
1. ábra. A korong alakú struktúrát kívülről érő nyomó erő csökkenő felületre hat, ezért a centrum felé haladva sűrűbbek az erővonalak, és ennek mértékében növekszik a nyomás. A nyomóerő iránya megegyezik a gravitációs vonzás irányával
Nem kell tehát szofisztikált sötét anyag térképeket rajzolni, hogy magyarázzuk a csillagok közel azonos keringési sebességét a Tejútban, elég ehhez figyelembe venni a galaxis alakját. A görbületi profil 1/R2 karakterisztikája helyett kialakuló 1/R függést mutatja a 2. ábra.

2. ábra. Görbületi profilok a spirális karok síkjának peremén. Az antigravitációs kompresszió összenyomja a galaxist és átalakítja a piros vonallal jellemzett 1/R2 lefutású Newton gravitációs profilt 1/R lefutásra, egyezően a MOND elmélettel (szétváló fekete vonal). A kék vonal mutatja az inverziós határnál előjelet váltó kepleron profilt külső kompresszió nélkül.
Összegezzük az elmondottakat! A vázolt kozmológiában a sötét anyagnak tulajdonított gravitációs erőt az univerzum százmilliárdnyi galaxisának préshatása helyettesíti. A kiegészítő erő az einsteini koncepció szerint kiegészített görbülettel értelmezhető. Ez úgy fogható fel, hogy a hatalmas kiterjedésű intergalaktikus tér hiperbolikus geometriájában elszigetelt elliptikus mélyedések vannak, ezek a galaxisok, melyekben a görbületet lefelé nyomja az antigravitációs préshatás. A helyes kérdés nem is az, hogy milyen többleterő tarja vissza a csillagokat, hanem az, hogy miért gyorsul fel a keringés. A viriál elv alapján adhatunk erre választ. Ez az elv összeköti a potenciális és a mozgási energiát, mégpedig a gravitációs erő távolságfüggése alapján a mozgási energia a potenciális energia fele lesz. Mivel a gravitációs potenciált az antigravitáció felerősíti, ez együtt jár a kinetikus energia növekedésével, ami pedig a csillagok keringési sebességének felgyorsulását idézi elő.
A Tejút peremétől befelé haladva a centrum irányába, elérünk egy határhoz, amin belül már az 1/R2 szerint változó gravitációs erő lesz domináns, ez okozza, hogy a galaxis magjában megjelenik egy gömb, illetve rúdszerű alakzat. A galaxis lapos szerkezete is a préshatásnak tulajdonítható, hiszen a síkra merőlegesen nincs jelentős kifelé ható centrifugális erő. Számtalan fonal és síkszerű elrendezést lehetett megfigyelni galaxis halmazokban, ami szintén az antigravitációs nyomás jelenlétére utal.
Az antigravitációs préshatásra épülő koncepció lényeges hozadéka, hogy feloldja a sötét anyag eloszlására és nagyságára vonatkozó magyarázatok ellentmondásait. Így például a Coma szuperhalmaz esetén a 10 millió fényév sugarú objektum óriási felületén adódik össze a nyomóerő, ami magyarázza, hogy miért kapott Zwicky olyan nagy értéket (450 szerest) a sötét anyag mennyiségére. A Tejút felülete ennél már jóval kisebb, ezért ott a sötét anyag mennyiségére jóval kevesebb (hatszoros) értéket kaptak. Világossá válik a Tejút csillagtérképének eloszlása is. A külső nyomóerő nem tökéletesen szimmetrikus, ami forgatónyomatékot gyakorol a galaxisra, és forgásba hozza. Ez a forgás hozza létre a spirálkarokat és alakítja ki a lapos korongalakú formát. A korong vastagsága azért kisebb, mert a síkra merőlegesen nem lép fel centrifugális erő, ami ellensúlyozná a külső nyomást.
 3. ábra. A Tejút oldalnézeti képe. A kék vonal mutatja a gravitációs erőt, a piros az antigravitáció préshatását
3. ábra. A Tejút oldalnézeti képe. A kék vonal mutatja a gravitációs erőt, a piros az antigravitáció préshatását
Az antigravitációs préshatás segítségével elkerülhetjük az olyan kínos magyarázkodást is, ami a „Nagy Vonzó” feltételezésére vezetett. Kimutatható ugyanis, hogy a Tejutat magában foglaló nagyobb halmazban nem érvényes a vöröseltolódás Hubble szabálya, ami avval magyarázható, hogy a Tejút meglepően nagy (600 km/s) sebességgel rohan egy másik galaxishalmaz felé. Ezt magyarázzák avval, hogy létezik egy megfigyelhetetlen és Tejútnál akár milliószor nagyobb szuperhalmaz, és ez fejt ki vonzó hatást. Ennek láthatatlanságát úgy magyarázzák, hogy balszerencsénkre a keresett objektum épp a Tejút síkjának túloldalára esik, és így a Tejút eltakarja előlünk. Nem könnyebb ezt úgy magyarázni, hogy az antigravitációs erők egyenetlenségei adnak lökést galaxisunknak?
Néhány szó az univerzum szerkezetéről
Felvethető a kérdés, hogy van-e a térgörbület mértékének felső határa? Einstein egyenlete nem ad meg ilyen határértéket. Fekete lyukak kialakulása rendkívül nagy tömegsűrűséget igényel. Arra számos csillagászati megfigyelés utal, hogy fekete lyukak tényleg léteznek. Ezek képződéséhez leginkább a neutron csillagok lehetnek alkalmasak nagy anyagsűrűségük miatt. Ez felveti azt a kérdést, hogy mikor válhat dominánssá a gravitációs erő az erős kölcsönhatással szemben? Ehhez is adhat járulékot a külső antigravitációs nyomás, elősegítve a nagyobb anyagsűrűség kialakulását.
Az Einstein egyenletnek azonban létezik olyan elfajult megoldása is, amit féreglyuknak neveznek. Ez elvben lehetővé tehet olyan „utazást”, amely meghaladná a fénysebességet. Ennek kísérleti ellenőrzése természetesen lehetetlen, ezért felmerül a kérdés, lehet, hogy ekkor az érvényességi határ túllépéséről van szó?
Az univerzumban a galaxisokat hatalmas méretű üres tér veszi körül. Mi ennek az oka? A választ a galaxisok hatalmas száma adja meg, amely egyrészt az antigravitációs taszítás miatt széttolja a galaxisokat, másfelöl pedig nyomásával összepréseli a csillaghalmazokat. A hiperbolikus geometria kialakulása geometriai szükségszerűség, amit görbületkiegyenlítési szabálynak nevezhetünk. Ha a térben létezik nagyszámú negatív görbületű centrum, akkor azokat a köztes tartományban pozitív görbületek veszik körül, ahogy a hegyek is völgyekkel váltakoznak.
Az univerzum hatalmas galaxisközi terének hiperbolikus geometriájára csillagászati adatok is utalnak. Becslések szerint itt a H atomok sűrűsége rendkívül kicsi, nem haladja meg az egyet köbméterenként. A H atom tömegét alapul véve a (8) összefüggésben megadott gravitációs határ 20 cm, vagyis kisebb, mint az atomok távolsága az intergalaktikus térben, és ezért nem jön létre gravitációs vonzás az atomok között a galaxisokat elválasztó térben. Ellenkező a helyzet a Tejút csillagközi terében, ahol köbméterenként az atomok száma már millió körül van, vagyis a csillagközi tér gravitációsan összekötött kontinuum. Másszóval a galaxisban nincsenek hiperbolikus „lyukak”.
Einsteinnek a tér görbületére vonatkozó koncepcióját a LIGO7 kísérletek [7Laser Interferometer Gravitational-Wave Observatory] is alátámasztják. A metrikus tenzor 10 független paraméteréből felépíthető egy olyan kombináció, amely megfeleltethető az általunk bevezetett görbületnek, a többi 9 paraméter a téridő aszimmetriáját írja le. Hogyan jöhet létre térbeli aszimmetria? Erre példa két fekete lyuk találkozása, mert a közöttük lévő tengely kijelöl egy irányt. Összeolvadáskor eltűnik a tengely és a térbeli szimmetria megszűnése rengeti meg az univerzumot, ami rezgést idéz elő a LIGO kísérletben szereplő két egymásra merőleges kar interferométerében.
Összefoglalás
Einstein általános relativitáselmélete fényt derített a gravitáció eredetére, de mint minden törvényt, így egyenletét is az teszi teljessé, ha meghatározzuk az érvényességi határokat. A koncepció lényege a tér görbült struktúrája, amely azonban nemcsak gravitációs vonzást, hanem antigravitációs taszítást is létrehozhat. Ez a taszítás okozza az univerzum tágulását, és teremti meg a galaxisok elliptikus tartományait körülvevő hiperbolikus teret, amelynek geometriai alapvetését Bolyai János és Lobacsevszkij adta meg. A sötét anyag és sötét energia fogalma a kozmológiából kiküszöbölhető, mert meggyőzőbb magyarázatot kínál a galaxisok közötti antigravitációs taszítás, amelynek préshatása tömöríti és stabilizálja a csillaghalmazokat,és magyarázatot kínál a gravitációs lencsehatás anomális intenzitására is.

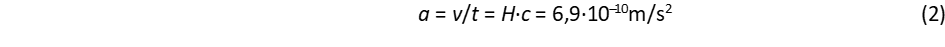
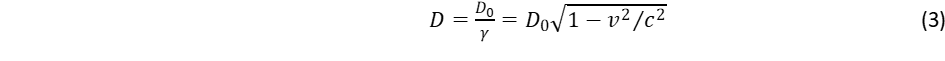
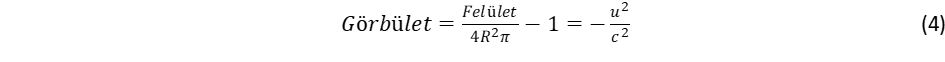
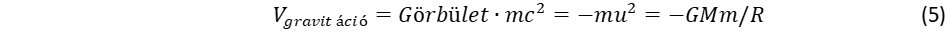
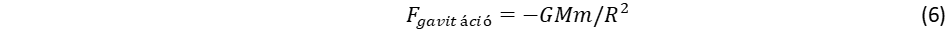
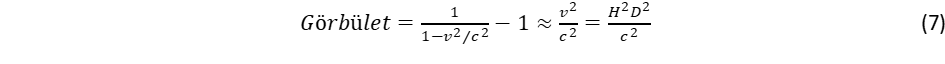



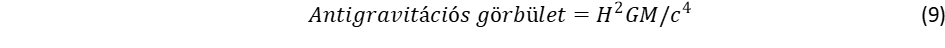
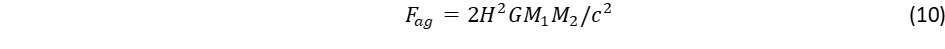


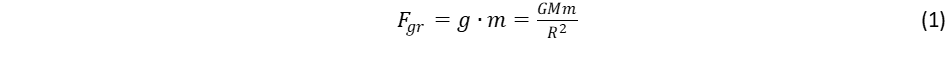

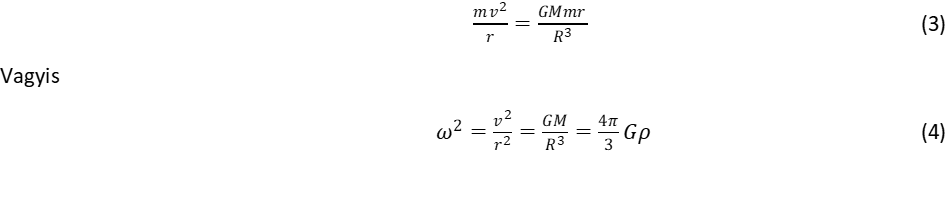

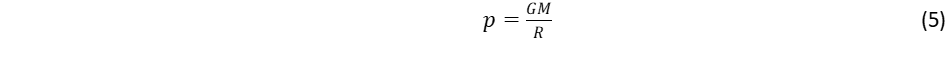

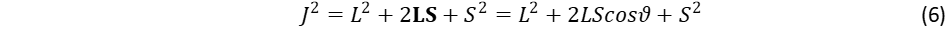
 (1)
(1)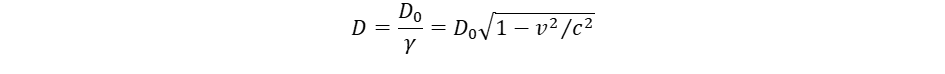 (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7) ___________________________________________________________________________________
___________________________________________________________________________________ (8)
(8) (9)
(9) (10)
(10) (11)
(11)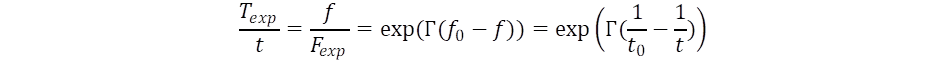

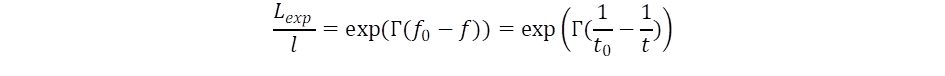
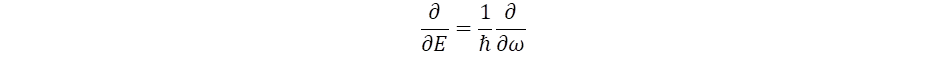 differenciálhányadostól, ahol felhasználtuk az E = h·f = ħω Planck-törvényt is, melyben ω = 2πf a körfrekvencia. Ez alapján vezethetjük be az idő operátorát a frekvencia szerinti differenciálhányadossal definiálva:
differenciálhányadostól, ahol felhasználtuk az E = h·f = ħω Planck-törvényt is, melyben ω = 2πf a körfrekvencia. Ez alapján vezethetjük be az idő operátorát a frekvencia szerinti differenciálhányadossal definiálva: