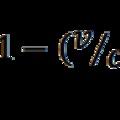A Dirac egyenletről már szó volt a korábbi bejegyzésben: „A Dirac egyenlettől az általános fermion egyenletig”, de most visszatérek erre a témára, mert a mikrovilág fogalmi rendszere szempontjából alapvető, hogy jól értsük, ez az egyenlet valójában miről is „szól”.

Az energia két alapformája

Az energiát két tag összegeként értelmezzük, az egyik, amelyik a mozgások következménye, ez a kinetikus energia, a másik valamilyen erőmezőben való pozíciótól függ, ezt nevezzük potenciális energiának:

E = E_kin + E _pot

Az általam javasolt fénysebességű forgásokból felépülő részecskekoncepció szerint a fizikai objektum elemi összetevői maguk is végeznek valamilyen belső – fénysebességű – mozgást. Ez a belső mozgás azonban nem szerepel a hagyományos fizikai képben, ezért pontosítani kell az előző megfogalmazást: egyfelől a kinetikus energia a külső (tehát szokásos) és belső (vagy saját) mozgások együttesét tartalmazza, másfelől a potenciális energiában a pozíciófüggésen kívül burkoltan megjelenik a belső mozgások hatása is.

Az energia relativisztikus törvénye

A relativisztikus mechanika alaptörvénye az energia kovariáns alakjára épül:

E² = c².p² + m²₀.c⁴

ahol az első tagot tekintik a relativisztikus kinetikus energiának, a másodikat a részecske nyugalmi energiájának. A fénysebességű forgásmodellben ez új értelmet nyer, mert nyugalmi energia helyett a belső mozgástól származó kinetikus energiáról kell beszélni, azaz a kinetikus energia két tagból tevődik össze:

E²_kin = E²_külső + E²_belső

A két tag négyzetes összeadási szabálya azt fogalmazza meg, hogy a teljes impulzus két tagja p = p_külső + p_belső úgy összegződik négyzetre emeléskor, hogy a kereszt tag eltűnik. Ennek azaz oka, hogy a belső mozgás gömbszimmetrikus pályán történik, aminek átlagértéke nulla és csak a belső mozgás impulzusának négyzete rendelkezik nullától különböző értékkel.

Az elektromágneses mező energiája

A Dirac egyenlet az elektron elektromágneses mezőben való mozgását írja le, ami szükségessé teszi a klasszikus elektrodinamika Maxwell egyenleteinek alkalmazását. Ezek az egyenletek eleget tesznek a relativisztikus kovariancia elvnek, amiért az elektromos és mágneses mező által keltett energiát hozzávehetjük a mechanikai energiához. A mozgásból származó tagot, ami a kinetikus energiához ad járulékot az áramok (töltésmozgás) képviselik és ezt az A(r) vektorpotenciál képviseli, aminek a töltéssel való szorzata adja meg az energiát. Lényeges, hogy bár vektorpotenciálról beszélünk, ez a tag nem potenciális energia, mert a mágneses mező a mozgó töltésekre hat és a töltés mozgása által jön létre, így a kinetikus energiához ad járulékot. Az energia kifejezésben a vektorpotenciált a töltéssel szorozzuk, amelyet viszont a részecske sajátmozgásának tulajdonítunk a fénysebességű forgásmodellben. Emiatt az e. A(r) tag voltaképp a külső és belső mozgások csatolódása. Az elektromos mezőben való energiát a Φ(r) skaláris potenciál és a töltés szorzata adja meg, és ez a töltésen keresztül szintén függ a belső mozgástól, de nem függ a külsőtől, emiatt az e.Φ(r) tag a potenciális energiát határozza meg. Így kapjuk meg a klasszikus elektron kovariáns energiaformuláját:

(E – e.Φ(r))² = (c.p – e.A(r))² + m²₀.c⁴

A kovariáns egyenletben tehát azt kell látni, hogy a Φ(r) potenciál a vizsgált rendszerben lévő töltések, az A(r) vektorpotenciál pedig az áramok eloszlását írja le, a p impulzus a vizsgált részecske külső térbeli mozgásmennyisége, az e töltés és az m₀ nyugalmi tömeg a részecske sajátmozgását fejezi ki.

A relativisztikus energia kvantummechanikája

A fenti egyenlet kvantummechanika átírását Klein és Gordon adták meg, de egyenletük nem volt kezelhető a szokásos sajátérték módszerrel az energia négyzetes alakja miatt. Ezt oldotta meg Dirac, amikor a négyzetgyökvonást 4x4 dimenziós spinorokkal hajtotta végre. Szemléletesebb képet kapunk, ha a spinorokat felbontjuk Pauli mátrixokra a mátrixok direktszorzat művelete alapján. Ekkor a Dirac egyenlet:

H_D = c.σ_x*σ(p – e.A(r)) + σ_z*I.m₀.c² + I*I.e.Φ(r)

Itt * a direktszorzást, a vastag betű a vektorokat, az aláhúzás mátrixokat jelöl, külön feltüntettem az I kétdimenziós egységmátrixot is. A direktszorzatban lényeges a tényezők sorrendje is. A Pauli mátrixok alakja:

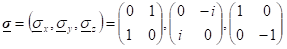
Alapvető jelentősége van a Dirac egyenletben, hogy az impulzus tagban σ_x, míg a nyugalmi energiában σ_z szerepel, ugyanis a két mátrix szorzatában a tényezők sorrendje nem cserélhető fel. Ebből származik a mozgási tömeg sebességfüggése ( lásd „A Dirac egyenlettől az általános fermion egyenletig” című bejegyzést.)

Kétértékűségek megjelenése az energiában és a lyukelmélet

 A négyzetgyökvonás sajátsága a kétértékűség, mert a negatív és pozitív számok négyzete azonos. A négyzetgyökvonás kétértékűségét azáltal őrzi meg a formalizmus, hogy a diagonális σ_z mátrixban a két elem előjele fordított, és így szükségképpen lesz pozitív és negatív energia. Abból az elvből kiindulva, hogy a nagyobb energiájú állapotból a rendszer spontán módon átmegy az alacsonyabb energiájú állapotba az következik, hogy az elektron előbb utóbb végtelenül nagy negatív energiájú állapotba ugrik, azaz megsemmisül. Ez viszont ellentétes a tapasztalattal, amely szerint az elektron stabilis részecske. Emiatt állt elő Dirac avval a hipotézissel, hogy a végtelen számú negatív energia állapot már eleve be van töltve a vákuumban és a Pauli elv kizárja, hogy az elektron a negatív energiájú pályára ugorjon. Ez persze azt jelenti, hogy a vákuum végtelenül nagy negatív tömeggel rendelkezik, ami mutatja a hipotézis abszurditását. A meghökkentő hipotézis mégis igaznak látszott, mert mintegy „megjósolta” egy új részecske létezését, amit nem sokkal később felfedeztek, nevezetesen a pozitront. Itt a lyukelméletről van szó, hiszen ha a negatív energiájú elektrontengerből hiányzik egy részecske, akkor az pontosan a pozitronnak felel meg (azonos a tömege, de ellentétes az előjele az elektronhoz képest) és még az is érthetővé válik, hogy az elektron és pozitron ütközése miért vezet a két részecske megsemmisüléséhez.  

A lyukelmélet látszólagos igazolása két fontos tanulsággal is jár. Egyfelől nagyon óvatosnak kell lenni, hogy mikor tekintünk egy elméletet bizonyítottnak, másfelől nem árt, ha a fizikusok is hallgatnak időnként a józanész szavára.

Negatív energia és az időtükrözés

Először is nézzük meg, hogyan lehet a negatív energia megjelenését magyarázni a formalizmusban? Az energia kovariáns egyenlete négyzetes tagokat tartalmaz, ezért van negatív energiájú megoldás a négyzetgyökvonás kétértékűsége miatt. A kvantummechanika mint hatást definiálja az energiát, amely arányos az idő szerint differenciálhányadossal: ℏid/dt. Ez azt jelenti, hogy a negatív energia az idő irányának megfordításának felel meg, más szóval a kovariáns reláció nem tudja megkülönböztetni, hogy a jelenből a jövő felé, vagy fordítva a múlt felé vesszük az irányt. Az már a legősibb tapasztalatok közé tartozik, hogy nem lehet visszatérni a múltba. Emiatt az alkalmazott matematikai formalizmust kell kiegészíteni egy kiválasztási szabállyal, ami megtiltja a negatív energiájú állapotba való átmenetet, és nem fordítva a természettől kell elvárni, hogy engedelmeskedjen egy matematikai egyenlet követelményeinek. Ennyit a józanészről. A másik kérdés hogyan magyarázzuk az elektron-pozitron annihilációt. Ez már a kettősforgás teóriájából következik. Minden kettősforgás két alapszimmetriával rendelkezik a két forgás egymáshoz képesti viszonya miatt, amit jobb és balkéz kiralitásnak nevezhetünk. A két részecske ütközésekor az ellentett forgások megsemmisítik egymást és így csak egyetlen forgás marad fent, amit a fénysebességű forgásmodellben mint fotont értelmezünk.

A spin és az időtükrözés

Elemezzük tovább a Dirac egyenletet! Az impulzus is négyzeten szerepel, ezért az impulzusnak is kétféle előjele lehet. Ezt fejezi két a második tényező σ, ami az elektron spin definíciójához vezet. A spin két forgásirányának tükrözését tekinti a kvantummechanika az időtükrözés műveletének. Ezt az időtükrözést meg kell különböztetni az energiára vonatkozó megállapítástól, mert az energia esetén a külső és belső mozgás együttes megfordításáról van szó, míg a spin esetében csak a külső mozgás ideje fordul meg.

Kettősforgások a királis térben: az általános fermion egyenlet

Az általános fermion egyenlet felírásánál 8x8-as spinorokat használtam, amelyben még fellép egy a Pauli mátrixokból felépített unitér mátrix is, amely definiálja a töltés és a tömeg operátorát. Ennek eredete a kovariáns egyenletben, hogy a nyugalmi tömegre vonatkozó tag is négyzetes, azaz itt is fent áll a kétértékűség, amiért egy harmadik kétdimenziós mátrix bevezetése is szükséges a teljes leíráshoz.  Ez az új mátrix nem az időhöz, hanem a térhez kapcsolódik és annak kétféle királis szimmetriája (jobb és balkezű) határozza meg a részecskék szerkezetét, azáltal hogy megmondja, milyen arányban részesül a két alapszimmetria a részecskét meghatározó kettősforgásban. Az elektron és pozitron tiszta királis állapot (jobb vagy balsodrású), a neutrínóban a két kiralitás kioltja egymást, míg a kvarkok képviselik a két kiralitást aszimmetrikusan tartalmazó forgásállapotot. Ennek megfelelően beszélünk tömeg, illetve impulzus sajátállapotú részecskékről. A tömeg sajátállapot egyúttal a töltés sajátállapotot is jelenti. A neutrínó nincs sem töltés, sem tömeg sajátállapotban, de jól definiált impulzussal rendelkezik, ez magyarázza, hogy létezhet három különböző neutrínó bár tömegük várható értéke nulla. Megfigyelhető részecskéknek vagy tömeg, vagy impulzus állapotban kell lenniük, mivel a kvarkok esetén egyik feltétel sem teljesül így szabad kvark nem is létezik.

Megjegyzés: A korábbi bejegyzések összefoglalását lásd: „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”