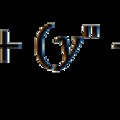Folytatás a "Fénysebességű forgások ...." első részétől, [5] lábjegyzet

A szekuláris egyenlet:                                   

Az itt bevezetett x változó E/c = m.c -nek felel meg az energia és a tömeg ismert összefüggése miatt, azaz

Innen már megkapjuk a relativisztikus tömegnövekedés jól ismert képletét:

Az általános fermion egyenlet

A sajátforgás kiralitása nem szerepel a Dirac-egyenletben, ezért ennek beépítésével érhetjük el, hogy valamennyi fermion mozgását le tudjuk írni elektromágneses térben. Kiinduló pontunk, hogy a bővített egyenlet is feleljen meg a relativitás klasszikus mozgástörvényeinek. A Dirac által elvégzett mátrixfelbontás nem csak 4 dimenziós, hanem 8 dimenziós spinorokkal is elvégezhető. Ennek módja, hogy a direktszorzatok terét egy további kétdimenziós térrel, a fermionok tulajdonságait meghatározó királis térrel bővítjük ki. 

A pozitron pozitív és az elektron negatív töltését leírhatja a királis térben értelmezett  σ_z mátrix +1 és -1 sajátértéke. Bevezetünk egy töltés operátort, amelynek diagonális elemei adják meg a fermionok töltését, azaz nullát a neutrínó, ±2/3e és ±1/3e értéket az „up” és „down” típusú kvarkok esetében. Ennek érdekében a Pauli-mátrixok lineáris kombinációiból felépítünk egy operátort és annak adjungált párját:

U_n = σ_z.cos ρ + σ_x.sin ρ és U†_n = -σ_z.sin ρ + σ_x.cos ρ

Az így definiált két operátor szorzata a Pauli-mátrixokhoz hasonlóan anti-szimmetrikus:

U_n.U†_n = - U†_n.U_n

Ennek az operátornak az elemi töltéssel való szorzata definiálja a töltésoperátort: 

Q = U_n.e

Ekkor a Q operátor diagonális elemei megadják valamennyi elemi fermion töltését, ha bevezetjük a cos ρ = n/3 szabályt és n = 3, 2, 1 vagy 0. Ezt úgy is értelmezhetjük, hogy az elemi fermionok a királis térben négy különböző formációt alkotnak, amit az n kvantumszámmal jellemezhetünk, a részecskéket és anti-részecskéket pedig az operátor két diagonális eleme különbözteti meg. Az U_n operátor azonban nem csak az elemi részecskék töltését, hanem tömegét és impulzusát is meghatározza. Ezt illusztráljuk a nyugalmi tömeg és az impulzus operátor segítségével, amit a tömeg illetve energia kétdimenziós (pozitív, negatív) terében definiálunk:

M₀ = U_n._.m₀    és         P = U†_n.p 

A töltés, tömeg és impulzus operátorokat a Dirac-operátorba helyettesítve írhatjuk fel az általános fermion operátort: 

H_F,n = c.U†_n●σ●(I.p – U_n.e.A(r)) + U_n●I●I.m₀.c² + I●I●U_n.e.Φ(r)

Az U_n és U†_n mátrixok szorzatának anti-szimmetriája miatt ez az operátor is megfelel a relativisztikus invariancia követelményének hasonlóan a Dirac-operátorhoz. 

Minden n értékhez tartozik egy részecske és egy antirészecske az n = 0 neutrínó kivételével, ahol az antineutrínó operátora megegyezik a neutrínóéval. A különböző fermionokat szemlélteti a következő ábra:

Fermion állapotdiagram a bal és jobbsodrású forgási frekvenciák koordináta síkjában. A sugarak mutatják a töltést, a körívek a nyugalmi tömeget. Kvarkok és neutrínó esetén csak az első generációs részecskéket tüntettünk fel. A frekvenciaskála nem lineáris, csak a trendeket mutatja

 Az n = 3 kvantumszám visszaadja az elektron energia operátorát, a σ_z operátor +1 és -1 sajátértékei különböztetik meg az elektront és a pozitront. Érdekes tanulságot vonhatunk le az n =0 (neutrínó) és az n = 1 és 2 kvark egyenletből. Neutrínó esetén a töltésoperátor diagonális elemei nullák, ezért ekkor a skalár és vektor potenciál elhagyható:

H_F,0 = c.σ_z●σ●I.p + σ_x●I●I.m₀.c²

Ekkor az impulzus és a tömeg szerepe felcserélődik: a nyugalmi tömeg lesz nem-diagonális és az impulzus lesz diagonális. Mivel mérni csak a diagonális elemeket tudjuk, így a neutrínót nullatömegű, de véges impulzusú részecskének kell tekinteni. Ebben tehát hasonlít a fotonhoz, ahol az egytengelyű forgások miatt nincs se tömeg, se elektromos töltés. A neutrínónak azért lehet véges az impulzusa, mert az impulzusnövekedés is végtelen fénysebesség esetén és így a térpontok határértékben nulla impulzusa szorozva a végtelenhez tartó növekedési faktorral véges értéket adhat. A neutrínó véges tömegének létrejötte tehát analóg jelenség, ahogy az elektronnál és más fermionoknál a térpontok határértékben nulla tömegéből a fénysebességű forgások által létrejön a véges nyugalmi tömeg. Valamennyi kísérlet, amelyben meghatározták a neutrínók haladási sebességét, a fénysebességet hozta ki. Ez megfelel annak a követelménynek, ami a fénysebességhez köti a neutrínók impulzusának létrejöttét.

A Standard Modell három neutrínó típust különböztet meg, amit elektron, müon és tau típusú részecskének neveznek. A Standard Modell eredetileg nulla nyugalmi tömeget rendelt ezekhez a részecskékhez, amit látszólag cáfol a neutrínó oszcilláció jelensége, amely szerint a három típus egymásba alakulhat. Mivel a neutrínók rendelkeznek véges impulzussal, így valóban lehet három különböző típusuk nulla nyugalmi tömegük ellenére. Úgy is fogalmazhatunk, hogy szemben az elektronnal, amelyik rendelkezik a referencia rendszer választásától független saját (nyugalmi) tömeggel, a neutrínó rendelkezik a referencia rendszertől független saját impulzussal és a hozzá tartozó mozgási tömeggel. Ez az m₀ =  p/c mozgási tömeg szerepel a tömeg mátrix nem-diagonális elemeiben:

H_F,0 = (σ_z●σ.p + σ_x●I.p)c

Kvarkok esetén mind a töltés és a tömeg egyaránt tartalmaz diagonális és nem diagonális elemeket, azaz a kvarkok nincsenek sem töltés, sem tömeg sajátállapotban. Ennek felel meg, hogy csak „renormált”, tehát nem valódi tömegről beszélhetünk és nem lehet kísérletileg detektálni ezeket a részecskéket

Záró gondolatok

A fotonokra érvényes közvetlen kapcsolatot az energia és impulzus között kiterjesztve valamennyi elemi részecskére eljuthatunk egyfelől a relativitáselmélet transzformációs törvényeihez, másfelől a fénysebességű forgások koncepciójáig.  Dirac eredeti gondolatát továbbfejlesztve 8-dimenziós spinorok bevezetésével a töltést, tömeget és impulzust is 2x2 dimenziós mátrixokkal reprezentáljuk, ami olyan a relativisztikus hullámegyenlethez vezet, amelyik alkalmas valamennyi fermion elektromágneses kölcsönhatásainak leírására. Ebben a reprezentációban ez elektront és pozitront mint tömeg-, a neutrínót impulzus-sajátállapotú részecskét definiálhatjuk, a kvarkok viszont nincsenek sem töltés, sem tömeg sajátállapotban. A különböző típusú neutrínók közötti oszcilláció értelmezhető a részecskék eltérő sajátimpulzusával. 

A blog további begyzéseinek összefoglalóját lásd "Paradigmaváltás a fizikában"

 Rockenbauer Antal