Szimmetriatörés: amikor a semmiből valami lesz

Einstein vetette fel a tér aktív szerepét, amikor arra a gondolatra jutott, hogy az anyag, pontosabban annak tömege, megváltoztatja a tér szerkezetét, aminek következtében a tömegek kölcsönhatásba lépnek, és ez a gravitáció. Higgs is a tér és anyag kapcsolatából indult ki, amikor kereste a tömeg eredetét, és azt a tér szimmetriájával hozta összefüggésbe. Koncepciójának lényege, hogy a szimmetriatörés vezet az anyag megszületéséhez, legalább is az ősi részecskéhez, amely bomlásával utat nyit a tömeg megjelenéséhez. De mi határozza meg a szimmetria fokát, ami megtörik, vagyis alacsonyabb szintre kerül? A megkülönböztethetőség! Az üres térben semmi sincs, a semmi pedig nem különböztethető meg a semmitől, ezért az üres tér szimmetriája maximális, ez a totális szimmetria. De mi az a mechanizmus, ami lebonyolítja a szimmetriatörést?  Erre keressük a választ a fénysebességű forgás koncepciójával. Az első lépcsőfok a pont megszületése, egy objektum, ami kijelöli a dimenzió nélküli pontot. Ez a pont egy olyan gömb, amelynek sugara, felülete és térfogata egyaránt nulla. Három dimenzióban létezik a világ, a pont helyének kijelölése három irány találkozási helye. De mi határozza meg az irányt? Ezt három fénysebességű forgás határozza meg, de ezekhez a forgásokhoz nem jár térbeli kiterjedés, ez maga a szingularitás. Olyan pontot képzeljünk el, melynek helye három nyíl metszéspontja, a nyilak hossza nullára zsugorodik, viszont a nyilak feje megmarad. A három irány már kétféleképp kapcsolódhat, lehet jobb és balkéz szimmetriájú, ez a kiralitás. A Higgs bozon születése ezért az első megkülönböztetés, ami szétválaszt két „valamit”, a kétféle kiralitást. Eljutottunk így az anyagi pont saját, belső szimmetriájához. Ennek az objektumnak még nincs kiterjedése, nincs „lapátja”, amivel nyomatékot gyakorolhatna a környező térre, nincs ezért spinje, és töltése sem. Csak a forgáshoz kapcsolódó energiája van. Ezt az energiát elosztva c²-tel beszélhetünk ugyan tömegről, de ez csak látens tömeg lesz, mert sem tehetetlenséget, sem gravitációt nem rendelhetünk hozzá.

A Higgs bozon kívülről és belülről

Eddig arról volt szó, hogy mit láthatna elvben a külső megfigyelő, persze csak elvben, hiszen a Higgs bozon rövid élettartama miatt kizárólag bomlástermékein keresztül azonosítható. De most vegyük fel varázsköpenyünket és bújjunk be a bozon belsejébe. Ott már más világ tárul fel elénk, ami kívülről csak egy pont volt, belülről már egy gömb lesz. A gömb sugarát a három tengely körüli ω frekvencia határozza meg. Viszont a teljes forgás együttvéve háromszor járja be a 2π tartományt, vagyis a teljes periódus 6π lesz, amiért a 3D forgás frekvenciája ω_3D = ω/3 lesz. Ennek azért van jelentősége, mert a fénysebességű forgás koncepciójában a tehetetlen tömeget a teljes forgás frekvenciája adja meg: minél nagyobb a frekvencia, annál nagyobb a tömeg, melynek váltószáma a redukált ħ Planck állandó:

m_3D = ħ ω_3D = ħ ω/3

Ennek akkor van jelentősége, ha összehasonlítjuk a Higgs bozon tömegét a belőle képződő fermionokkal. A 2D forgású fermionok esetén a tömeget az ω_2D gömbfrekvencia határozza meg

m_2D = ħ ω_2D = ħ ω/2

Ez felel meg a fermion S = ½ spinjének. A Higgs bozon bomlásakor képződő fermionok számára a frekvenciaarányok miatt az eredeti 3D tömeg másfélszerese áll rendelkezésre, vagyis a kiséletileg meghatározott 125 GeV/c² tömeg bomlása 187,5 GeV/c² fermion tömeggel egyenértékű. Emiatt pedig a Higgs bozon bomlása már képes fedezni a top kvark 156 és 176 GeV/c² közé becsült tömegét is.

Ha már ott vagyunk a bozon belsejében, érdemes jobban körülnézni, mert ez segít megérteni a kvark világ további rejtélyeit. A belső és külső világ különbsége megjelenik a spinben és töltésben is. Vajon miért nulla mindkettő a Higgs bozon esetén? Azért mert ezeket a tulajdonságokat kívülről látjuk! A fénysebességű forgás minden dimenziót nullára csökkent, ezért nincs olyan sugár, amelyik a lendület nyomatéka lehetne, és így a spin nulla lesz. De miért nincs töltése se a Higgs bozonnak? Ennek oka, hogy a QED elmélet által megkövetelt virtuális fotonok, amelyek közvetítik az elektromos kölcsönhatást, nem kerülnek kibocsátásra. Mediátor nélkül pedig töltés sem jöhet létre. A töltés eredetét a kiralitással kötöttük össze, bár a Higgs bozon rendelkezik kiralitással, de nincs ami ezt „üzembe helyezze”. A foton S = 1 spinnel rendelkezik, a Higgs bozonnak viszont nincs spinje, így az egy fotonos emisszió és abszorpció nem valósulhat meg a spin megmaradási törvénye miatt. A S = ½ spinű fermionoknak azért lehet töltése, mert a vetületi kvantumszám +½-ről -½-re való ugrása már fedezi a foton S = 1 spinjét.

A Higgs bozon belsejében való kutakodásunk megvilágítja a kvarkok háromféle színtöltésének eredetét, sőt érthetővé teszi az elektromos töltés harmadolását is! A háromdimenziós forgás felfogható három egymásutáni egydimenziós forgásnak, de felbontható egy két dimenziós gömbforgásra és egy egydimenziós forgásra is. Jelöljük a kétdimenziós forgásokat az x, y, z forgástengelyekkel, ezek lesznek az xy, yz és zx gömbforgások, ezeket tekinthetjük a három kvark előzetes állapotának, melyek a bozon felbomlása után alkotják a barionok és mezonok seregét. Bár a Higgs bozonnak nincs valódi töltése, de a kiralitás miatt beszélhetünk a +e, vagy –e látens (nem realizálódó) töltésről. Ez a látens töltés épül fel a három elő-kvark töltéséből. Lehetne-e mindhárom elő-kvark töltése 1/3e? Nem mert ekkor a három kvark töltése nem tudná kiadni a bozon nulla külső töltését. Erre csak úgy van mód, ha van egy 2/3e töltés, amit kiegyenlít két -1/3e töltés, az előbbit hordozza az up típusú kvark, az utóbbit a down. A kvarkok kísérletileg megfigyelhetetlen harmadolt töltése tehát a Higgs bozon belső és külső világának viszonyából fakad.

A megfigyelhető részecskék születése a szimmetriatörés további fokozataiban valósul meg. A három ekvivalens tengely körüli fénysebességű forgás közül az egyik elmarad, így véges kiterjedésű lesz az egyik dimenzió. Ekkor olyan gömböt kapunk, melynek a felülete nulla, de már van sugara. A gömbszimmetria még megmarad, de belép a következő megkülönböztető „valami”: a véges sugár és  a nulla felület különbsége. Ezek a kéttengelyű gömbforgások, a fermionok. Van már sugaruk, amely nyomatékot gyakorolhat, lesz így spinjük és töltésük is, sőt „lapátjukkal” már a környező teret is megforgatják, lesz ezért gravitáló tömegük is. Így megy lejjebb a pontszerű alakzat magasabb szimmetriája a véges sugarú gömb szintjére. A kvantumfizikában a szimmetriát kvantumszámok kísérik, egy rendszeren belül nem lehet két fermion azonos kvantumállapotban, mert akkor elvész közöttük a megkülönböztethetőség, ezt fejezi ki a Pauli elv és a Fermi-Dirac statisztika. A barionok kvarkstruktúrája fedi fel a kvarkok további tulajdonságát, mely szerint háromféle színkvantumszámot vehetnek fel, ennek oka a háromféle gömbforgás: az xy, yz és zx létezése. A kvarkok színkvantumszámán alapul az erős kölcsönhatás elmélete, a kvantumkromodinamika.

A szimmetria még lejjebb megy, amikor a kettős forgás egyik tagja ”kinyílik”, és a gömbszimmetria átadja helyét a henger szimmetriának, ezek a bozonok. Tengely irányuk már tetszőleges lehet, helyet biztosítva a megkülönböztethetőségnek, ezért nem tiltja semmilyen kvantumszabály, hogy hányan lehetnek azonos állapotban, ez a Bose-Einstein statisztika.

De miért létezik két különböző fermion típus, a kvarkok és a leptonok családja? Ez keletkezésük sorrendjéből következik. A Higgs bozon bomlásakor első lépésben jönnek létre egyfelöl a kvarkok, másfelöl a W és Z bozonok (a Z bozonról később), majd ezután a W bozon bomlása szüli meg a leptonokat. Tehát a kvarkok egy lépésben, a leptonok két lépésben alakulnak ki az „ősi” részecskéből, azaz a kvarkok elsődleges, a leptonok másodlagos bomlástermékek. A Higgs bozonban még összekapcsolt kettősforgások a bomlás után is együtt maradnak, ami stabilizálja a kvarkokat, melyek hármasával (barionok), vagy kettesével (mezonok) vannak összekapcsolódva. Az összekapcsolási erőt közvetíti a nyolc gluon az erős kölcsönhatás kvantumkromodinamikai elméletében. A három kvarkos részecskékben, vagyis a barionoknál, a három S = ½ spin együttese kiadhat S = ½, vagy 3/2 értéket (dublett és kvartett), a töltés pedig lehet nulla (például a neutron), vagy ±e (pl. proton), de lehet ±2e is. A két kvarkos struktúrákban, vagyis a mezonoknál, az eredő spin lehet nulla vagy egy (szingulett és triplett), a töltés pedig, 0 és ±e (semleges és töltött). A barionokat vagy három anyagnak, vagy antianyagnak tekintett kvark, a mezonokat egy kvark és egy antikvark építi fel. Mit tekintünk anyagi, vagy és antianyagi kvarknak? Azt a Higgs bozon belső kiralitása dönti el.

Hogyan alakítja át a gyenge kölcsönhatás bozonja a fermionokat?

A Higgs bozon elsődleges bomlásakor létrejön háromféle két dimenziós gömbforgás, azaz három kvark, és egy gyengekölcsönhatási W bozon. Ez utóbbi egydimenziós forgás, akárcsak a foton, de eltérő a szimmetria, mert a W bozon nem a tengely irányában terjed c sebességgel, hanem arra merőlegesen a forgási síkban. Ez okozza, hogy változik a forgási sugár. Viszont a sugár és a frekvencia szorzata c, vagyis állandó, amiért a W bozon frekvenciája is változik. Ez teszi a gyenge kölcsönhatás bozonját hasonlóhoz egy „csavarkulcshoz”, amelyik képes egymásba alakítani a különböző fermionokat. A fermionok két alaptípusának, a kvarkoknak és a leptonoknak (elektron, müon, tau, valamint a neutrínók) három generációja van, melyek tömegükben, azaz forgási frekvenciájukban különböznek. Ez a részecskefizika újabb titokzatos hármassága, melyet két határ jelöl ki, a felső határt kvarkok esetén a Higgs bozon tömege szabja meg, leptonoknál pedig a W bozon. Minél gyorsabban forog egy részecske, annál gyorsabban bomlik el. Az alsó határt már a részecskék stabilitása hozza magával, mert az elektron és az alapgenerációjú kvarkokból felépülő proton már nem bomlik tovább.

Nézzük meg részletesebben a W bozon „csavarkulcs” szerepét. A kulcsfogalom nem is a tömeg, hanem a forgási frekvencia. Ennek a frekvenciának kell „ráhangolódni” az átalakítandó fermionok frekvenciakülönbségére. Ennek mechanizmusa megegyezik a foton szerepével, amikor átmenet jön létre az elektron két állapota között. A fotonhoz egy jól definiált ω körfrekvencia tartozik, amely meghatározza a foton energiáját, amikor létrejön, vagy átmenetet hoz létre az elektron két állapota között:

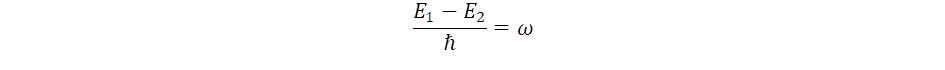
Ugyanezt teszi a W bozon is, amikor két kvark állapotot átvisz egymásba, melynek energiáját a renormált tömegekkel adhatjuk meg, de itt a frekvenciaszabályban különbséget teszünk a fermion ω_2D gömbfrekvenciája és a bozon ω körfrekvenciája között:

Ebből a szabályból adódik, hogy a kvark átmenetek számításakor a W bozon tömegének kétszeresét kell figyelembe venni. Ide tartozik az a kérdés is, hogyan jön létre a nagytömegű (80 GeV/c²) W bozon a neutron béta-bomlásának első lépésében, hiszen a W bozon tömege csaknem két nagyságrenddel haladja meg a kibocsátó neutronét (0,9396 GeV/c²). Ebben segít a W bozon frekvenciapásztázó képessége. Itt jegyezzük meg, hogy ez a frekvenciapásztázás, vagyis energiaváltozás, nem sérti az energiamegmaradás elvét, mert a forgás kinetikus energiáját kiegyenlíti a tér lokális görbületének negatív potenciális energiája.  A béta bomlás során spontán emisszióval létrejön a W^- bozon, amely frekvenciát vesztve eljut ahhoz a frekvenciához, ami egyezik a neutront alkotó down és up kvarkok frekvencia különbségével. Ekkor következik be -1/3e töltésű down állapot ugrása a 2/3e töltésű up állapotba (ez az abszorpciós lépés). Ezt követően bomlik el a W^- bozon egy-egy elektron és neutrínó létrehozásával. Ez a folyamat két megmaradási törvényt teljesít: a töltésre és a spinre vonatkozót. Hasonló módon közvetíti a W bozon a leptonok átalakulását is.

A W bozon frekvenciapásztázása alkalmas arra, hogy a legnagyobb tömegű kvark átalakulását is közvetítse a top és a bottom állapot között. Az utóbbi renormált tömegét 4,2 és 4,7 GeV/c²-re becsüli a szakirodalom, ezért a két állapot tömegkülönbsége 150 és 170 GeV/c² között lehet. A W bozon frekvenciájának duplázódási szabálya miatt 160 GeV/c² tömegkülönbségű átmenet lehetséges, ami épp a két határérték közé esik. Létrejönnek azonban olyan kvark átalakulások is, ahol a töltés nem változik. A folyamat mediátora egy további bozon, a semleges töltésű, vagyis királisan semleges Z bozon. A semlegesség azt jelenti, hogy a kétféle kiralitású forgás egymásba ötvöződik, vagyis azonos valószínűséggel van jelen. Ennek tömege még nagyobb: 91 GeV/c², ami a duplázódási szabály miatt 182 GeV/c² tömeggel ekvivalens. Erre a többletre szükség is lehet, amikor a top kvark a második generációs charm-ra, vagy az első generációs up-ra alakul át, mert ezek kisebb tömege miatt nagyobb a kvark átmenet két állapotának energiakülönbsége.

Végeredményként megállapítható, hogy a fénysebességű forgás modell összhangot teremt a szubatomi részecskék tömegei között. A Higgs bozonra pedig olyan forgásmodell adható meg, amelyből származtatni lehet a bomláskor képződő részecskék természetét, valamint geometriai magyarázat adható a törttöltésű kvarkok eredetére és az új kvantumszám, a színkvantumszám megjelenésére.