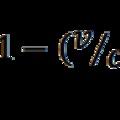A külvilágból érkező információk hatása gondolkodásunk fogalmaiban tükröződik. A mikrovilágból érkező információk oly mértékben térnek el megszokott környezetünkből érkező megfigyelésektől, hogy az megköveteli alapvető fizikai fogalmaink hozzáigazítását az elérhető információk jellegéhez.  Ez a fogalmi adaptáció azonban fájdalmasan hiányzik a mai fizikai gondolkodásból, ami számtalan zavart, félremagyarázást idéz elő mindenekelőtt a kvantummechanikában és a részecskefizikában. A szükséges fogalmi adaptáció irányába tesz kísérletet a következő írás.

A klasszikus fizika fogalomrendszere

Az elsődleges fogalom, amit a klasszikus fizika az anyaghoz rendel a tömeg, illetve folyadékok és gázok esetén a térfogategységre jutó tömeg, azaz a sűrűség. Ez a tömeg kvantitatív jellemzője az anyag mennyiségének, ami kapcsolódik az oszthatóság fogalmához. Az anyag mennyisége a feldarabolás során annak tömegével együtt változik. Az oszthatóságnak azonban határa van, amikor eljutunk az atomig, illetve a molekulákig.

 A tömeg mellett a következő alapfogalom a mozgás. Mozognak az égitestek, mint a Föld és a Hold, de megfigyelhetjük a labda vagy a madarak mozgását is, de mozognak a különböző közegeket alkotó részecskék, atomok és molekulák is. A lényeg, hogy mindig van valami „ami mozog”, itt azon van a hangsúly, hogy először kell létezni valamilyen anyagnak, ami tömeggel rendelkezik, és ez végzi a mozgást. Más szóval az anyag, illetve a tömeg mélyebb fogalmi szintet képvisel, mint a mozgás.

A pályafogalom folytonossága

 A testek mozgásáról a fény hozza számunkra az információt, amit vagy kibocsát, vagy visszatükröz a test. A klasszikus mechanika abból indul ki, hogy tetszőleges pontossággal és tetszőleges sűrűséggel érkezik hozzánk információ a test helyzetéről, vagyis az s(t) pályafüggvény folytonos és differenciálható. A differenciálhatóság miatt ebből képezhetjük a v(t) = ds/dt sebesség és az a(t) = ds²/dt² gyorsulás függvényt. A mozgásmennyiség jellemzésére vezetjük be az impulzus (a lendület) fogalmát. Ha egy pingpong labda üt meg minket, alig vesszük észre, de ha egy azonos sebességű teniszlabda, azt már jókorát lök rajtunk, míg a futball labda le is dönthet minket lábunkról. Ennek a lökő hatásnak nagyságát adja meg a p = mv impulzus.

Az erő fogalom

A fizika feladata az okok felderítése: miért olyan a mozgás menete, ahogy azt a megfigyelt s(t) pályafüggvény mutatja? Ezt az okot adja meg az erő fogalmának bevezetésével. Ha a test mozgásállapota (azaz p = mv impulzusa) nem változik meg, vagyis a sebesség állandó, akkor azt mondjuk, hogy a testre nem hat külső erő. Ha viszont a sebesség változik, azaz a gyorsulás nem nulla, akkor azt az erő hatásának tudjuk be. Ez az erő passzív, utólagos definíciója, amikor a hatásból következtetünk vissza a ható erőre. A mozgásállapot leírásához azonban ennél többre van szükség: a kölcsönható erőt az anyag immanens tulajdonságaként kell megadni, például megmondani, hogy milyen erő lép fel a tömegek és a töltések között, illetve milyen erők hatnak az atomok belsejében. Ehhez ad kulcsot, ha megadjuk, milyen reláció köti össze a pályafüggvényt és az erőket.

Fizikai törvények infinitezimális megfogalmazása

Ezen a ponton kell felvetni a kérdést, milyen kapcsolat építhető fel a mozgást létrehozó erő és annak hatása között. Két út kínálkozik, a véges méretű pályát köthetjük össze a mozgást megváltoztató okkal. A másik út, amikor az infinitezimális tartományra korlátozódjunk, ahol határértékben nullához tartó változásokról van szó. Ennek előnye, hogy itt minden kölcsönhatás egyszerű arányosságra korlátozódik. Ezt alkalmazta Newton is, amikor kimondta az erő és a gyorsulás arányosságát:

F = ma

Az m tömeg mint arányossági tényező szerepel az összefüggésben, ami a test mozgásának tehetetlenségét jellemzi. A tömeg ezáltal kettős szerephez jut, egyrészt hat rá egy erő, ami elindítja a mozgást, ez bolygómozgás esetén a gravitációs erő, másrészt ennek az erőnek „ellenáll”, azaz tehetetlenséggel is rendelkezik. A newtoni törvény megfogalmazható az impulzus segítségével is kapcsolatot teremtve az erővel:

F = dp/dt

A Newton törvény és az energiamegmaradás

A mozgási pályák azonban véges kiterjedéssel rendelkeznek, amit a differenciális Newton egyenlet vonalmenti integrálásával határozatunk meg. Így jutunk el a mechanikai energia megmaradási tételéhez:

½mv² + V_pot = p²/2m+ V_pot = E

Ez vezet el a felismeréshez, hogy az erő hatására történő változás mögött megbújik egy állandó mennyiség: az energia. Ez fejezi ki a fizikai gondolkodás célját: megtalálni az állandóságot a változásban.

A fenti formulában a V_pot potenciális energia az erő integráljából származik, amit a mechanika az erő munkavégzésének nevez. Ez a munkavégzés hozza létre a kinetikus energiát, amely pedig az ma kifejezés integrálja. Ezért az energiamegmaradás törvénye voltaképp a Newton egyenlet integrális alakjának tekinthető. A két törvény viszonyát úgy is megfogalmazhatjuk, hogy a változás törvényéből indulunk ki, de utunk végén eljutunk az állandósághoz, a megmaradáshoz.

A fenti ekvivalencia szabály azonban csak kis sebességeknél érvényes, és módosul a helyzet, amikor a v sebesség már közel van a fény c sebességéhez. Ennek oka, hogy a tér és idő koordináta transzformációja független egymástól, amíg a választott inercia rendszer sebessége kicsi, de nagy sebességnél már a tér koordináták a mozgás irányában lerövidülnek (Lorentz kontrakció), míg az idő koordináta dilatációja következik be. Ennek következtében a Newton egyenlet integrálja már más alakú kinetikus energiát eredményez:

Ezt nevezik a relativitáselméletben az energia kovariáns alakjának. Bár a formula látszólag jelentősen eltér a kinetikus energia nem-relativisztikus alakjától, könnyen belátható, hogy ha pc kicsi az m₀c² nyugalmi energiához képest, akkor visszakapjuk a kinetikus energia megszokott alakját.

A fény is anyag!

A kovariancia törvény fizikai lényegének megértése érdekében térjünk rá a fény, illetve annak egysége, a foton tulajdonságaira. Kiindulópontunk, hogy a fény is anyag! Mégpedig az anyag különleges formája, amihez nem tartozik nyugalmi tömeg. Ennek megértése azért nehéz, mert a tömegnélküliség szembemegy klasszikus felfogásunkkal az anyagról, amely az anyag létezését a tömeghez köti. A fény természetének megértésében a Maxwell egyenletek adják a kulcsot, amely a fényt a vákuumban c sebességgel terjedő elektromágneses hullámokhoz rendeli. De mi az a közeg, amelynek hullámai megalkotják az elektromágneses mezőt? Ez a kérdés azért merül fel, mert ha hullámokra gondolunk, legyen szó a víz hullámairól, vagy a hangról, a mögött mindig valamilyen közeg áll, melynek atomjai, vagy molekulái végzik összehangolt mozgásukat. Ez a gondolkodás vezette Maxwellt is, aki valamilyen különös közeget képzelt el, amit nevezhetünk éternek is, amelynek fodrozódása alkotja meg az elektromágneses hullámokat. Az éter fogalom bevezetése azonban nem oldja meg a kérdést, csak továbbhárítja. Mert azonnal hozza magával a további kérdést: de milyen anyag alkotja ezt a rejtélyes étert? Richard Feynman, aki a Maxwell egyenletekben a fizika nagy felfedezését üdvözli, meg is „rója” Maxwellt ezért a koncepcióért. Feynman felfogását matematikai fetisizmusnak is nevezhetjük, mert a fizikai realitás helyett megelégszik a matematikai formalizmus ellentmondás mentességével, és elégnek érzi, ha matematikai formulák kerülnek a fizikai objektumok helyére. 

Harmadik út: az alapfogalmak sorrendjének megfordítása

Jelenleg is ez a két felfogás viaskodik egymással, de létezik-e harmadik út, amelyik következetes képet rajzol fel a fotonok, sőt valamennyi részecske fizikai természetéről? Itt kell elgondolkodni azon, hogy milyen információ áll rendelkezésre, amiből az elemi részecskék szerkezetére következtethetünk. Az almát meghámozhatjuk, vizsgálhatjuk annak belsejét, de az elektront nem lehet meghámozni, az elektront nem lehet feldarabolni, nem lehet megnézni, hogy mi van az elektron belsejében, ilyen típusú információt nem nyújtanak számunkra a nagyenergiájú szóráskísérletek. Tudhatjuk viszont az elektronról a mágneses mezőben történő vizsgálatok révén, hogy spinnel, azaz impulzusnyomatékkal rendelkezik. A fotont sem lehet feldarabolni, de tudjuk, hogy összeköthet egymással két távoli elektront. Az egyik állapotváltozása kibocsát egy fotont, amely valahol a távolban, akár fényévekre megváltoztathatja egy másik elektron állapotát, például, amikor távoli csillagok fénye a szemünkbe jut. Van tehát kölcsönhatás, van tehát mozgás, de ehhez nem járul tömeg. A kölcsönhatásból viszont tudjuk, hogy a fotonnak van impulzusa és spinje is. A forgás indikátora a spin, amellyel valamennyi részecske rendelkezik, márpedig impulzusnyomatéka csak véges kiterjedésű forgó objektumoknak lehet. Ezért mondhatjuk, hogy valamennyi részecske elválaszthatatlan tulajdonsága valamilyen forgás.

Ez alapján juthatunk el a következtetéshez, hogy a részecskevilág elválaszthatatlan és elsődleges tulajdonsága a mozgás. Ebben még könnyű egyetérteni, de merészkedhetünk-e ez alapján újrafogalmazni az anyag és mozgás viszonyát? Ehhez már kopernikuszi bátorságra van szükség, mert gondolkodásunk alapkategóriáját kell megfordítani, meg kell fosztani trónjától a tömeghez kötött anyag primátusát. Ki kell mondani, amikor a részecskék világában járunk. már nem az anyag az elsődleges, ami mozog, hanem a mozgás válik elsődlegessé, amely megteremti az anyagot. Mégpedig nem akármilyen mozgásról van szó, hanem a fénysebességű forgások rendszeréről. Ezek alkotják a részecskevilág két alapkategóriáját a fermionokat és a bozonokat.

Ebben a felfogásban már nem az az alapkérdés, hogy „mi forog”, hanem az, hogy honnan származik a tömeg, milyen az az elsődleges mozgás, ami a tömeg létrehozásáért felelős. Hogyan értelmezhetjük ennek alapján a részecskék két főtípusát, a fermionokat és a bozonokat? A fermionokat kettős, azaz gömbforgások hozzák létre, szemben a körforgással, ami a bozonokat, így az elektromágneses kölcsönhatás közvetítőit, a fotonokat alkotja meg. A spint az határozza meg, hogy milyen nagyságú az a forgási tartomány, ami ismétlődéshez vezet, amikor az eredeti irány újra visszatér. Körforgás esetén ez 2π, ami megfelel az S = 1 spinnek, szemben a gömbforgás 4π ismétlődési periódusával, amihez az S = ½ spin tartozik.

Az energia és impulzus ekvivalenciája

A fotonokhoz nem tartozik nyugalmi tömeg, mert létüket a körforgás mellett a c sebességű terjedés definiálja, vagyis a foton számára nyugalmi állapot nem létezik. Zéró nyugalmi tömeg esetén a kovariancia törvényből következik, hogy az energia arányos az impulzussal:

E = pc

A foton nem rendelkezik tömeggel, viszont van impulzusa, azaz lökő hatása, ami pedig a mozgás mennyiségi jellemzője. Tehát van impulzus, azaz mozgás, de nincs tömeg! Az impulzusnak két forrása lehet, az egyik a test sebessége, a másik a fénysebességgel terjedő és nullatömegű elektromágneses hullám frekvenciája, illetve hullámszáma. A Planck törvény szerint E = ħω, amiért p = ħω/c = ħk, ahol ω a körfrekvencia és k a hullámszám. Az impulzus definíciója megfelel a de Broglie féle szabálynak is.

Az impulzus ezért alapvetőbb fizikai kategória, mint a nyugalmi tömeg. Az E = pc ekvivalencia pedig alapvetőbb reláció, mint a tömeg és energia E = mc² ekvivalenciája!

A kovariancia törvény fizikai alapja

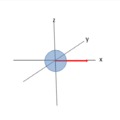
Térjünk most rá az elektronra, vagy bármelyik nyugalmi tömeggel rendelkező fermionra. A kovariancia törvény voltaképp csak azt fogalmazza meg, hogy az impulzusnak két összetevője van, az egyik a részecskét alkotó belső impulzus. Erre ugyanaz a szabály érvényes, mint az elektromágneses hullámokra, vagyis ez az impulzus fénysebességű forgástól származik és arányos a forgási frekvenciával. Az elektromágneses hullámoktól annyiban tér el, hogy gömbszimmetriájú kettős forgásról van szó, amely kijelöl egy centrumot és létrehozza a részecske tömegét. A másik impulzus komponens már a belső forgás által létrehozott tömeg külső mozgásától származik. A teljes impulzus a kettő eredője:

p = p_k + p₀

Az impulzus vektor négyzete:

p² = p_k² +2p_kp₀ + p₀²

Fermionoknál a belső forgás gömbszimmetrikus, ezért összegzésben a kereszttag eltűnik. Alkalmazzuk az energia és impulzus ekvivalenciáját, ekkor az

E² = p_k²c² + p₀²c²

összefüggéshez  jutunk. A „teremtő” belső forgás miatt p₀ = m₀c, és így eljutottunk a kovariancia törvényhez. Így válik magától értetődővé a relativitáselmélet energia törvénye is. Amikor sikerül a probléma gyökeréig hatolni, jutalmunk a felismerés, hogy a fizika alaptörvényei roppant egyszerűek. Például a kovariancia törvény mögött is csupán az impulzus két komponensének összeadási szabálya áll. Nem kell tehát egy különös, láthatatlan anyag, amelynek hullámzása hozza létre vákuumban a fény elektromágneses mezejét, vagy kitölti a fermionok belsejét. Alternatívát adhatunk a matematikai fetisizmus számára is, mert a matematikai formalizmus támaszkodhat egy konzekvens fizikai modellre, amely a fénysebességű forgásokon alapul.

Kiegészítő megjegyzések

A fénysebességű forgás által létrehozott tömeg az üres (tehát forgásmentes) térből szintén összhangba kerül a kovariancia törvénnyel. Ha ott alkalmazzuk az E = mc² ekvivalenciát és átrendezzük az egyenletet, eljutunk a tömeg sebességfüggését leíró formulához:

Ha a v sebesség határértékben c-hez tart, akkor X értéke végtelen lesz. A nullatömegű forgásmentes tér tömegét 1/X-nek – azaz nullának – választva már véges tömeget kapunk.  Tehát a tömeg létrejöttének kulcsa a tömegnövekedés szingularitása. Az a kérdés is felmerül, hogy miért van nyugalmi tömege a fermionnak, és miért nincs a fotonoknak. Ennek oka a forgás szimmetriája: a gömbforgás kijelöl egy centrumot, ahová rendelhetjük a tömeget, szemben a körforgással, amely csak egy tengelyirányt határoz meg, és így a tömeg nem lokalizálható.

Arra a kérdésre is választ ad a modell, hogyan lehet a nullatömegű fotonnak impulzusnyomatéka. Ez az E = ħω = pc Planck-törvényből következik, mely szerint p = ħω/c Ez egyébként megfelel a de Broglie féle hullámtermészet impulzusának is. Az ω körfrekvenciával forgó és c kerületű sebességű forgás sugarat R_c = c/ω. Ezt a sugarat szorozva az impulzussal kapjuk, hogy az impulzusnyomaték – függetlenül attól, hogy mekkora a forgási frekvencia – mindig a redukált ħ Planck állandó lesz.