Előadásom valószínűleg nem csak témájában, hanem felfogásában is szokatlan lesz. A jelenlegi kutatást a specializáció jellemzi, amely egy-egy szűk témát vizsgál rendkívüli alapossággal. Itt most ennek épp ellenkezőjéről lesz szó: különböző diszciplínák közötti kapcsolatkeresés lesz a tárgy, melynek során az elektron tulajdonságaiból kiindulva jutunk el a kozmológia nagy kérdéseihez.

Saját szakterületem az elektronspin-rezonancia spektroszkópia, ebből adódóan izgatott a kérdés, hogy valójában mi is a spin. Jelentése szerint forgás, vagy ha úgy tetszik perdület, de tényleg perdül-e, forog-e az elektron és a többi részecske, amelyik spinnel rendelkezik? Ha viszont forog, akkor fellép a centrifugális erő, amit valaminek ellensúlyozni kell. Ez vezetett el a következő kérdéshez, vajon szóba jöhet-e a gravitáció? Ennek einsteini elmélete szerint a téridő görbülete hozhat létre gravitációs erőhatást. De mi hozza létre a görbületet, vissza vezethető-e a forgásra a görbület? A speciális RE Lorentz kontrakciós szabálya szerint a forgó rendszer kivezet a nem-euklideszi geometriából, de ekkor milyen geometriához jutunk? Hogyan kapcsolódik össze a geometria és az erő, a tér forgásai tekinthetők-e mediátornak a tömegek között, miként a kvantumelektrodinamikában a foton, amely kapcsolatot létesít a töltések között? Így kerül be a képbe a QED módszertana. A téridő forgása kapcsolja össze a felsorolt diszciplínákat, amit a kepleron elvben foglaltam össze. Felmerült viszont bennem a gondolat, hogy létezik a tér gömbszimmetrikus mozgásának egy ellentétes párja is, amikor a gömbfelszínét befutó forgások helyett sugárirányú tágulás lép fel. Ez a tér tágulása, amely elvezetett végül a parányi elektrontól elindulva az univerzum nagy szerkezeti kéréseihez, a kozmológiához is.  Erről a szokatlan útról fog szólni előadásom.

Ismerkedjünk meg először a két világ nagyságrendjeivel, az egyiket képviselje a Föld, a másikat az elektron. A forgásokhoz, keringésekhez tartozó két fizikai mennyiség az impulzusmomentum, vagy mai szóhasználatban a perdület. Föld esetén a forgást 7*10 ³³ Js jellemzi az elektron spinje pedig 5*10^-35, az arány 68 nagyságrendi különbség. Ha a Föld keringő mozgását vesszük alapul a perdület mérőszáma 2*10⁴⁰ Js, míg az elektron pályákhoz nagyságrendben 10^-35 Js tartozik. Óriási tehát a különbség, de a mozgásukat tekintve mégis ugyanaz a fizikai állandó jellemzi tulajdonságaikat. A Föld és a bolygók mozgásait leíró tudomány a gravitáció elmélete, az elektron tulajdonságaival a kvantummechanika illetve a QED foglalkozik.

Amikor elindulunk utunkra, hogy kapcsolatot találjunk a fizikai különböző területei között, kérdéseket teszünk fel, de nagyon nem mindegy, hogy milyenek a kérdéseink. Ha jó az induló kérdés remélhetjük, hogy jó választ is kaphatunk, ha rossz az induló kérdés, annak az a jele, hogy a válasz során egyre több igazolhatatlan hipotézis láncolatába gabalyodunk bele. Hipotézisekre a tudományban persze szükség van, de ha a hipotézisek láncolata túl hosszú, akkor ideje van gyanakodni, hogy rossz volt a kiindulópontunk. Vegyük például Einstein fontos kérdését: Honnan származik a tömeg gravitációs ereje. Erre adott korszakos fontosságú válasza, amikor a téridő görbületével értelmezte a gravitációt. De a kvantummechanika térhódítása elvezetett egy rossz kérdéshez is, amikor mindenáron a kvantumvilágba akarták gyömöszölni a gravitáció elméletét is. Ennek következménye lett a húr, membrán és egyéb elméletek hosszú sora, amelyben egyre több láthatatlan térdimenzió feltételezésébe fogtak, és eljutottak a végtelen számú párhuzamos univerzum gondolatához is, anélkül, hogy akár egyetlen kísérleti eredmény is alátámasztaná a burjánzó elméletek sokaságát. Ez ösztönzött arra, hogy magam is feltegyek kérdéseket. Olyan kérdéseket vetettem fel, hogy miért görbül a téridő a tömegek körül, illetve, hogy mi a gravitáció mediátora. Ez vezetett el a kepleron koncepciójához, amely azonban nem kvantumos közvetítő. Ezt a koncepciót fejtem ki előadásomban.

A fizikai elméleteket két szinten fogalmazhatjuk meg: makroszkopikus és mikroszkopikus szinten, és keresni kell a két szint kapcsolatát. Ez utóbbira példa, ahol az elektrodinamika törvényeit kapcsolatba lehet hozni az elemi részecskék kvantumelektrodinamikai tulajdonságaival. Nehezebb ugyanezt az utat megtalálni a gravitáció elméletében. Newton fogalmazta meg a gravitáció elméletét, amikor a csillagok és bolygók tömegének gravitációs erőt tulajdonított, amely alapján sikeresen lehetett leírni a bolygó mozgások törvényeit. Ehhez tette fel Einstein a maga kérdését, amikor a gravitáció eredetét akarta megtalálni és bevezette a térgörbületek fogalmát, erre alapozva írta fel gravitációs egyenletét, amely alapján lehetett olyan anomáliákat is értelmezni, amire Newton egyenlete nem adott kielégítő magyarázatot. Ehhez a ponthoz teszem hozzá a magam kérdését: miért görbül a tér a tömeg körül? Ha elfogadjuk Einstein felvetését, mely szerint a téridő görbülettel rendelkezik, amelyik változik és követi az anyagmozgásokat, akkor már eljutottunk a tér mozgásaihoz. De akkor miért ne foroghatna a tér a tömeg körül, amely aztán megalkotná a tér görbült szerkezetét? De ez idáig még csak makro-szintű megközelítés. A QED elméletéhez kell nyúlni, ha a mikro-szintű magyarázatot keressük a gravitációra. Szükség van egy fotonhoz hasonló közvetítőre, amely azonban nem kvantumos. Ezt az indokolja, hogy amíg a töltés szigorúan kvantált jellegű, erre nem mutat semmi az elemi objektumok tömege esetén. Így formálódott ki a kepleron koncepció, amelyben megvalósul a részecske és a hullámtermészet is.

Hová lehet elhelyezni a kepleront a részecskefizika rendszerében? A részecskéknek két alaptípusa van: a feles spinű fermionok és az egészspinű bozonok. A fermionok térbeli pozícióval, töltéssel és tömeggel rendelkeznek és mozgásuk sebessége nem érheti el a fénysebességet. A bozonok legismertebb képviselője a foton, az elektromágneses kölcsönhatás közvetítője. Nincs tömege és töltése, de rendelkezik impulzussal, perdülettel és energiával is, emellett fénysebességgel halad. A fotonnak két típusát szokás megkülönböztetni, a megfigyelhető fotont, amely hírt ad a világról és a virtuális, vagyis megfigyelhetetlen fotont, amelyik az elektromágneses erőt hozza létre a töltések között.

A kepleron viszont tisztán virtuális részecske, nem rendelkezik spinnel, nincs tömege, töltése és saját energiája sem. Ez egy olyan gömbszimmetrikus térforgás, melynek sebessége követi a Kepler törvényt, ezért is neveztem el kepleronnak, szerepe a tömeggel rendelkező objektumok közötti gravitációs erő létrehozása a tér szerkezetének megváltoztatásával, amelyet fénysebességgel valósít meg. Mivel a kepleronnak nincs energiája, így kvantuma sincs.

A kepleront alkotó térforgások megértéséhez egy különleges mozgással kell megismerkedni, amelynek jellemzője a gömbszimmetria. Ha például a Föld forgására gondolunk, annak van egy kitüntetett tengelye, amelyik összeköti az Északi és a Déli sarkot. Ha a Föld keringő mozgására gondolunk, annak pedig kitüntetett  síkja van. Ezek olyan forgások, amelyek a kör 2π radián szögtartományát járják be. Ez egy szimmetriacsökkentő mozgási forma. A gömbszimmetrikus mozgás viszont a gömb teljes felületét járja be, mintha egyszerre két tengely körül történne a forgás, éppen ezért 4π szögtartományú forgásról kell beszélni. Ez egy szimmetriatartó mozgási forma! Erre példát a kvantummechanika ad, amikor az elektron gömbszimmetriájának az S = ½ spin felel meg, szemben a pályamozgással, amelynek kvantumszáma egész, azaz 2π szöget bejáró elektronpályákról van szó.

1. ábra. A kepleron gömbforgások, a radiális görbület és a Newton törvény kapcsolata

Itt eljutottunk ahhoz a ponthoz, amikor keressük a választ: hogyan vezet a gömbforgás a tér görbületéhez. Einstein egyenlete a téridő görbületét egy 4*4 dimenziós görbületi tenzorral – az un. metrikus tenzorral – írja le, mi viszont megelégszünk egy olyan sémával, amelyben egyetlen, un. radiális komponens jellemzi a görbületet, vagyis a tér gömbszimmetrikus marad. Ez természetesen egyszerűsítés, de indokolt, amikor gömbszimmetrikus objektumokról van szó, de fenntartható akkor is, ha a görbületet nagy távolságban vizsgáljuk a csillagászati objektumokhoz képest, például sok millió fényévnyire a galaxisoktól. A görbület meghatározásánál a speciális relativitáselmélet Lorentz kontrakciójából indulunk ki. Ez azt mondja ki, hogy a térkoordináta a mozgás irányában lerövidül, de változatlan marad arra merőlegesen. Körmozgásnál ez a kerület rövidülését jelent a 2πR szabályhoz képest, vagy gömbforgásnál a gömb felszíne lesz kisebb a 4πR²-hez képest. Ez az a csökkenés, ami megadja a radiális görbület definícióját, amit az ábrán a kék nyíl mutat. Behelyettesítve a Lorentz kontrakciót a görbület negatív lesz és kifejezhető a sebességég/c arány négyzetével. A gömbforgás sebességéről feltételezzük, hogy a Kepler szabályt követi, hasonlóan ahhoz, ahogy a kis tömegű objektumok keringenek a nagy tömegű Nap körül.  Úgy definiálhatjuk a gravitáció potenciális energiáját, hogy a dimenziómentes görbületet szorozzuk a relativitáselmélet ekvivalencia törvényének megfelelő mc² energiával. A potenciálisenergiából pedig a szokásos módon kapjuk meg a jól ismert Newton erőt. Itt most egy fordított utat jártunk be Newtonhoz képest. Ő a gravitációs erőből származtatta le a bolygómozgás törvényét, mi viszont a forgásból indultunk ki és úgy jutottunk el az erőtörvényhez. Azok számára, akik járatosak az Einstein gravitációs egyenletének matematikájában, itt feltüntettem még a radiális görbület kapcsolatát a metrikus tenzorral.

2. ábra. A gravitációs erő relativisztikus korrekciójának értelmezése a kovariancia elv és Eötvös ekvivalencia elvének összekapcsolásávl

Jöhet persze az ellenvetés: a kepleron modell magyarázza a klasszikus gravitációs törvényt, de Einstein általános relativitáselmélete ezt már túlhaladta, amikor egy relativisztikus korrekciót bevezetve magyarázni tudta a Merkúr bolygó perihéliumának eltolódását. Nos, ez az a pont, ami mutatni fogja, hogy mekkora hozadéka van, ha jól kapcsolunk össze különböző fizikai törvényeket. Az egyik a relativitáselmélet energia törvénye, a kovariancia elv, amely a mozgás kinetikus energiáját „beépíti” a tömegnövekedésbe. Ha például egy bolygó, így a Merkúr a Nap körül befogásra kerül, akkor kinetikus energiája révén nagyobb tömegre tesz szert. A másik törvényt Eötvös torziós ingával bizonyította, nevezetesen a tehetetlen és a gravitáló tömeg ekvivalenciáját. Nem kell mást tenni, mint a tömegnövekedést figyelembe venni a gravitációnál és eljutunk pontosan ahhoz a relativisztikus korrekcióhoz, amit Schwarzschild bravúros matematikával levezetett Einstein gravitációs egyenletéből kiindulva.

Érdekes következtetéseket vonhatunk le kötött rendszerek tömegdeficitjére is. Amikor a fúziós reakció felépíti a Hélium magot, nagymértékű tömegdeficit jön létre: az erős nukleáris kölcsönhatás révén hatalmas energiájú gammasugárzás keletkezik. A molekulákat összekötő kémiai kötés is okoz kismértékű tömegdeficitet, ami UV sugárzást hoz létre. Bolygó befogásnál az energia mérleg épp fordított, ekkor tömegnövekedés jön létre, jelezve hogy a gravitációs folyamatot nem kíséri energia kisugárzás.

Úgy tűnik hát, hogy az einsteini elmélet tökéletes leírást ad a bolygók mozgásáról a Naprendszeren belül. De mekkora is a Naprendszer? Nem nagyobb, mint egy fényév. Ha ezt összevetjük a Tejút hosszával az ennél 100 ezerszer nagyobb. Ha az egész univerzummal vetjük össze, akkor az arány több mint tízmilliárd! Biztos-e, hogy ilyen hatalmas távolságban is változás nélkül érvényesek a gravitáció törvényei? A Tejút centrumától távoli csillagok keringési sebessége például zavaró összefüggést mutat. Azt várnánk a newtoni elmélettől, hogy a külső tartomány csillagai egyre kisebb sebességgel keringenek. De mit mutatnak a csillagászati megfigyelések? A csillagok keringési sebessége a külső tartományban gyakorlatilag állandó, úgy másodpercenként 220 km/s. Ráadásul a Tejút számított tömege nagyon kevés ahhoz, hogy a spirális karok végein ellensúlyozni tudja a centrifugális erőt, vagyis le kellene szakadni a csillagoknak. Mi tartja egyben a Tejutat? Más hasonlóan zavaró megfigyelésekre vezetett a csillaghalmazok centrális sűrűsége: jóval nagyobbnak adódott annál, ami várható a halmazok össztömegéből. Az einsteini elmélet érdekes következménye a gravitációs lencsehatás, amely megsokszorozhatja távoli galaxisok képét. Ennek intenzitása is meghaladja az elmélet által várt értéket. Ezek az anomális jelenségek vezettek a sötét anyag hipotéziséhez! A számítások olyan eredményre vezettek, hogy a sötét anyag mennyisége hozzávetőleg hatszorosa a megfigyelhető, látható anyagnak!

Ennek az elméletnek is megvan az előzménye. Le Verrier francia matematikus érdeme volt a Neptunusz felfedezése. A bolygó mozgásokat elemezte és kiszámította, hogy a különböző bolygók mozgása hogyan befolyásolja egymást. Az Uránusz keringő mozgásánál olyan anomáliára bukkant, amit úgy lehetett feloldani, ha létezik egy további külső bolygó is. Ennek a feltételezett bolygónak meghatározta a lehetséges pozícióját, és amikor kérésére egy csillagász megvizsgálta a megjelölt helyet, azonnal rábukkant az új bolygóra, ami aztán a Neptunusz nevet kapta. Hasonló számítások a Merkúr bolygó esetén is anomáliát mutattak. Az ellipszis pálya perihéliuma fokozatosan elcsúszik a várt pozíciótól, de ezt a többi bolygó zavaró hatásával nem lehetett értelmezni. Ezért született meg egy legbelső láthatatlan bolygó hipotézise, ami a Vulkán nevet kapta. Viszont minden erőfeszítés kudarcot vallott, hogy ezt a bolygót meg is találják a csillagászok. A dilemmát végül Einstein oldotta fel, amikor gravitációs elmélete úgy módosította a newtoni törvényt, amely már pontosan értelmezte a Merkúr bolygó mozgásának anomáliáját. A láthatatlan Vulkán bolygó koncepciója ezért elvetésre került.

Nem lehetséges, hogy a sötét anyag koncepciója helyett is inkább azt kellene megnézni, hogy lehetséges-e módosítani a newton törvényt? Ebből indult ki egy izraeli fizikus, Milgrom is. Feltételezte, hogy nagy távolságban, úgy 1000 fényév felett a gravitáció nem a newtoni törvénynek megfelelően R²-el arányosan csökken, hanem lassabban. Ezt nevezzük a MOND (Modified Newtonian Dynamics) modellnek. Ha ügyesen választunk meg bizonyos paramétereket az erő egyenletben, akkor értelmezhetővé válik a csillagok keringési sebességének anomáliája. Ez eléggé ad hoc magyarázat, ráadásul nem minden jelenségre alkalmazható, amit magyarázni lehet, a sötét anyag hipotézisével, amiért a MOND elmélet nem vált széles körben elfogadottá. Ugyanakkor a sötét energián alapuló modellnek is vannak erősen vitatható pontjai. Az egyik a sötét anyagot alkotó feltételezett részecskék kimutatása. Nevet már kapott ez a részecske, a WIMP (Weakly Interacting Massice Particle) tucatnyi nagy nemzetközi projekt is indult, hogy megtalálják ezeket a részecskéket, de mindegyik teljes kudarcot vallott. A másik erősen vitatható kérdés a sötét anyag térbeli eloszlása. Térképeket ugyan lehet arról készíteni, hogy hogyan helyezkednek el valahol a galaxisok perifériáján, de arra nincs magyarázat, hogy milyen erők felelősek azért, hogy olyan különleges a sötét anyag eloszlása.

Még nem beszéltem a sötét energia kérdéséről, de ennek magyarázatát sem tudja elősegíteni a sötét anyag hipotézise. Honnan is indult a sötét energia hipotézise? Ennek megértéséhez ki kell lépni galaxisunkból és vizsgálni kell a távoli csillagokat. Ha egy csillag távolodik tőlünk, akkor hosszabb lesz az onnan érkező fény hullámhossza, ezt nevezzük vörös eltolódásnak. Ellenkező esetben, ha a csillag közeledik összetorlódnak a hullámok, ez a kék eltolódás. Hubble kezdte először vizsgálni ezt a jelenséget. Klasszikus csillagászati módszerekkel lehetett becsülni bizonyos távolságon belül az egyes galaxisok távolságát. Hubble érdekes felfedezésre jutott, ott ahol a vizsgált galaxis már 10 millió fényévnél távolabbra van, a fény vöröseltolódása növekszik a távolsággal, vagyis egyre nagyobb sebességgel távolodnak tőlünk a galaxisok. Ez vezetett el az Univerzum tágulásának koncepciójához. Későbbi mérések azt is kimutatták, hogy az Univerzum gyorsulva tágul. De milyen erő, milyen energia idézi elő a gyorsulva tágulást?  Ennek értelmezéséhez született meg a sötét energia koncepciója. Ennek előtörténete Einsteinhez nyúlik vissza. Amikor kidolgozta az általános relativitáselméletét sztatikus univerzumban gondolkodott és kellett egy erő, ami ellensúlyozza a gravitáció összehúzó erejét. Emiatt az egyenletben felvett egy mindenütt jelenlevő taszító tagot, amit Λ-ával jelölt, ez kapta a kozmikus állandó nevet. Később rámutattak, hogy az egyensúly fenntartásához ez nem elég, amiért Einstein maga is elismerte tévedését. Viszont Hubble felismerése után már nem kellett sztatikus Univerzumban gondolkodni, és nagyon „jól jött” ez a Λ tag a tágulás magyarázatához. Így jött létre, a jelenleg általánosan elfogadott Λ-CMD kozmológia, amely szerint az általunk megfigyelhető anyag nem több, mint az Univerzum 4-5 százaléka.

 A koncepció általános elfogadottságot mi sem mutatja jobban, hogy James Peebles, a kozmológia legfontosabb kidolgozója, ezért Nobel Díjat is kapott 2019-ben. Egy éve még eszembe sem jutott, hogy kételkedjek a sötét anyagra és a sötét energiára alapozott kozmológia helyességében. Viszont úgy egy évvel ezelőtt eszembe jutott valami: szimmetria szempontból az univerzum tágulása voltaképp épp a fordítottja a kepleron forgásoknak, valójában a tér két lehetséges gömbszimmetrikus mozgásáról van szó. Amíg a forgás a gömb felszínét csökkenti le, addig a tágulás a sugár csökkenését idézi elő. Ennek értelmében a tér tágulása átalakítja a kepleron szerkezetét és az eredetileg kibocsátott kepleronok már nem vonzást, hanem taszítást fognak közvetíteni a tömegek között.

A Kepler forgás sebessége csökken a távolsággal, vagyis csökken a negatív görbület, a Hubble tágulás sebessége viszont növekszik, tehát nagyobb lesz a pozitív görbület, amikor a két sebesség egyezik, a görbület kiegyenesedik. A tömegből kiáramló kepleronok megfordítják szerepüket, innen kezdve már nem vonzást közvetítenek, hanem taszítást.  Ezt a távolságot nevezzük a kepleron inverziós sugarának, ennek harmadik hatványa arányos az objektum tömegével és szerepel benne a G gravitációs állandó és a H Hubble konstans négyzete is. Először azt néztem meg, hogy mekkora távolságban történik meg a kepleronok inverziója a Tejút esetén. A szakirodalomban talált tömegadatból indultam ki, és ekkor ért a hatalmas meglepetés: az inverziós távolság 3,26 millió fényévnek adódott. Ennek az értéknek óriási jelentősége van, mert egyrészt jóval nagyobb, mint a Tejút kiterjedése, de csak kivételes esetben kerül két galaktika ennél közelebb egymáshoz. A Tejúthoz legközelebbi galaxis, az Androméda köd 2,5 millió fényévre van tőlünk. A galaxison belül tehát a gravitáció az úr, de a galaxisok csaknem kivétel nélkül mind taszítják egymást.

A galaxisok közötti taszításnak van egy nagyon szokatlan tulajdonsága: nem csökken a galaxisok távolságával! Honnan származik ez a különös tulajdonság? A kepleron koncepcióban az egyes atomok körül kialakuló térforgásokat tekintjük virtuális részecskéknek, amelynek intenzitása arányos a tömeggel, emissziós együtthatója G/c² és csökken a kibocsátástól vett R távolság négyzetével. A kepleronok a tér tágulását követve átalakulnak és megfordítják a radiális görbület előjelét, melynek nagysága a Lorentz kontrakció miatt a tágulási sebesség és c arányának négyzete lesz. A Hubble törvény szerint a sebesség a távolsággal arányos, ezért a távolság négyzetével arányos görbületet kapunk az egyes kepleronok esetén. Minthogy a tömegből kilépő kepleronok intenzitása R² szerint csökken bizonyos távolság fölött a görbület már állandó lesz.

Az antigravitáció távolságfüggetlenségének különös jelentősége van, mert emiatt az univerzum több százmilliárd galaxisának taszító hatása összeadódik. Ez a felismerés pedig egy csapásra több kérdésre is választ ad! A Tejutat minden irányból galaxisok százmilliárdjai veszik körül és mindegyik taszító erőt gyakorol rá. Ez egy hatalmas kompressziónak felel meg, és ennek nyomása nem engedi kiszakadni a gyorsan forgó csillagokat. Nincs szükség tehát a sötét anyag vonzó hatására, mert ennek szerepét helyettesíti az univerzum „nagy prése”. Az sem rejtély többé, hogy mi hozza forgásba a galaxist. Ez a kompresszió nem teljesen egyenletes, ami forgató nyomatékot gyakorol és forgásba hozza az egész csillaghalmazt. A préselő erő a galaxis halmazokat is összenyomja, ezért találunk anomális centrális koncentrációt. A nyomás hozzájárul a tér görbületéhez is, ami magyarázza a gravitációs lencsehatás intenzitását is. Sőt, a sötét energia eredete sem lesz rejtély többé, hiszen valamennyi galaxis taszítja egymást, így megtaláltuk annak okát is, hogy mi okozza az univerzum gyorsulva tágulását.

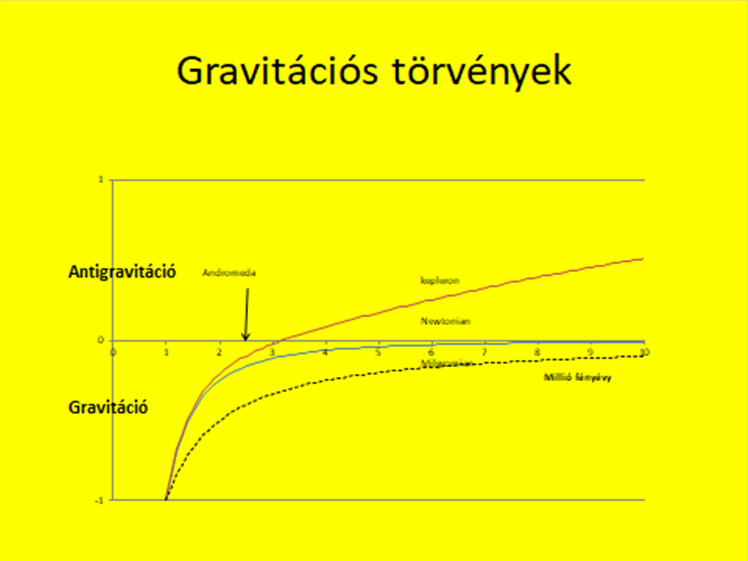
3. ábra. A gravitációs erő távolság függése a Newton (kék), a Milgrom (fekete szaggatott) és a kepleron (vörös) koncepció szerint
4. ábra. A gravitációs erő változása a Tejút határától az univerzum határáig logaritmikus ábrázolásban

A következő két ábrán mutatom be, hogyan változik a gravitációs erő a különböző modellekben. A kék görbével mutatott Newton erőhöz képest a Milgrom modell szerint lassabban csökken az erő, viszont a kepleron modell szerint gyorsabb a csökkenés, majd nagyjából az Androméda köd távolságában a vonzás taszításba megy át. A következő ábra logaritmikus skálán mutatja meg a gravitáció átmenetét antigravitációba. Nagyon széles tartományban gyenge és állandó nagyságú taszító erő lép fel a galaxisok között, de amikor közeledünk az univerzum határához, ahol a Hubble tágulási sebesség c-hez közeledik, felerősödik a taszítás. Ez arra utal, hogy a Tejút szerkezetére az univerzum valamennyi galaxisa hatást gyakorol, de ezen belül kiugróan nagy a szerepe a legtávolabbi galaxisoknak. Mivel az antigravitációs hatás is fénysebességgel terjed, ez azt jelenti, hogy az Ősrobbanás galaxisunk szerkezetére is döntő hatást gyakorol.

Térjünk még vissza annak magyarázatához, hogy a Tejút csillagjainak keringési sebessége miért nem változik a centrumtól való távolság függvényében. A sötét anyag koncepció ezt egy önkényes tömegeloszlással próbálja magyarázni, anélkül hogy indokolná, miért viselkedik így a sötét anyag. A külső kompresszió esetén nem szorulunk ilyen feltevésre. A Tejút spirálkarjainak vastagsága lényegében azonos. Külső kompresszió esetén az erőt a felülettel kell osztani, ami viszont az egyenlő vastagság miatt fordítottan arányos a centrumtól való távolsággal. Ez azt jelenti, hogy a külső nyomás a centrifugális erővel azonosan változik a sugárral, vagyis a csillagok keringési sebessége is azonos lesz.

 Korábban említettem, hogy mekkora a Tejút inverziós sugara. A Tejút tömegében viszont szerepelt a sötét anyag mennyisége is, ha ettől eltekintünk a sugár kisebb lesz, úgy 2 millió fényév körül, de ez a lényeget nem érinti. Viszont érdekes lehet egyéb fizikai objektumok inverziós sugara. Például a Hidrogén atomé 20 cm. Ez amiatt érdekes, mert a Tejút csillagközi terében a H atomok távolsága ennél jóval kisebb, vagyis az egész galaxis gravitációsan összekötött fizikai objektum. Más a helyzet a galaxisok közötti térben. Az ott becsült atomsűrűség már nagyon kicsi, hozzávetőleg ott az atomok átlagos távolsága 1m. Vagyis a galaxisközi térben már a hidrogén atomok között nagyon gyenge taszító erő lép fel.

Közepes méretű atomok esetén 1m körül van az inverziós távolság, kondenzált anyagokban az atomok távolsága ennél 10 nagyságrenddel kisebb. Ez azt jelenti, hogy az egyes atomok körüli görbült térstruktúra tökéletesen átfed, amiért a gravitációs erő arányos lesz a tömeggel. Voltaképp ez magyarázza az Eötvös által bizonyított ekvivalenciát a tehetetlen és a gravitáló tömeg között. 

Érdekes következtetéshez jutunk, ha az inverziós sugarat az egész univerzumra vonatkoztatjuk. A jelenleg elfogadott kozmológia szerint az univerzum kora 13,8 milliárd év, ami azt jelenti, hogy az univerzum kölcsönhatási sugara 13,8 milliárd fényév, vagyis ez a legnagyobb távolság, amelyen belül a gravitációs vagy antigravitációs hatás még elér hozzánk. Ezt alapul véve az univerzum tömegére kapunk becslést, ami 10⁵³ kg nagyságrendbe esik. Ez a Tejút tömegénél kb. 100 milliárdszor nagyobb. Ez a szám is jól egyezik a galaxisok csillagászatilag becsült számával.

Hátra van még egy érdekes kérdés, milyen a nem-euklideszi tér geometriája. Két irányban indulhatunk el: beszélhetünk elliptikus, azaz Riemann geometriáról, illetve hiperbolikus, azaz Bolyai-Lobacsevszkij geometriáról. Einstein általános relativitáselméletében mindig csak a Riemann geometriáról van szó, ennek oka, hogy ebben kizárólag gravitációs vonzásról van szó, amelyhez olyan geometria tartozik, amelyben a párhuzamosok összefutnak, illetve a kör kerülete az átmérőhöz viszonyítva kisebb, mint π, vagy ami ezzel ekvivalens a háromszög szögeinek összege nagyobb 180 foknál, azaz π radiánnál. A kepleron koncepció viszont arra utal, hogy a vonzás átmegy nagy távolságban taszításba, azaz ott a sugár és kerület aránya fordítva tér el π-hez viszonyítva. Ez azt jelenti, hogy a galaxisokon belül elliptikus a geometria, de a közöttük lévő tartomány már hiperbolikus. Úgy képzelhetjük el az univerzumot mint egy hatalmas mazsolás kalácsot, amelyben a mazsola elliptikus geometriájú, de maga a kalács, ami ezt magában foglalja hiperbolikus geometriájú. A kétféle geometria megjelenése szükségszerű, mert többcentrumú elliptikus geometriát csak hiperbolikus geometria övezheti. A teret csak úgy görbíthetjük meg, ha benne a völgyeket dombok és hegyek választják el. Ebből a szempontból az ősrobbanás utáni univerzum kivételt képez, mert ott a nagy anyagsűrűség miatt csak egyetlen centrum létezett. Az univerzumot szétfeszítő infláció és tágulás már megteremtette annak feltételét, hogy elkülönült centrumok, azaz galaktikák alakuljanak ki. Ez azt jelenti, hogy a kezdeti szétválást ugyan a gravitáció lelassította, de ennek folyamán megteremtődtek az antigravitáció feltételei, ami begyorsította a tágulási folyamatot, ez jellemzi jelenlegi univerzumunkat.

5. ábra. A Λ-CDM és a kepleron modell összevetése különböző csillagászati megfigyelés magyarázatában

A következő dián felsorolok néhány példát, amiben összevethetjük, hogy melyik kozmológia teljesít jobban. Ezt mindenki maga is végig gondolhatja. Talán egy példát azért kiemelnék. Ez a Great Attractor kérdése. Kimutatták ugyanis, hogy a Tejút bizonyos csillagkép irányában nagy sebességgel közeledik, ez alatt 600 km/s értéket kell érteni. A jelenlegi kozmológiában ezt úgy magyarázzák, hogy létezik a Tejútnál milliószor nagyobb csillaghalmaz, ami maga felé rántja galaxisunkat. De ha létezik egy ilyen óriási csillaghalmaz, hogyhogy mégse látjuk? Erre jön az ügyes hipotézis, mely szerint pechünkre úgy helyezkedünk el a Tejút síkjához képest, hogy az pont eltakarja előlünk. Ügyes magyarázat! A kepleron koncepcióban nincs szükség ekkora ügyességre, hiszen az antigravitációs nyomás egyenlőtlenségei könnyen okozhatnak olyan hatást, amelyik egyik irányban meglökheti a Tejutat.

Végül mi arra az esély, hogy a tudomány befogadja a kepleron koncepciót a Λ-CMD kozmológia helyett? Jelenleg nem túl nagy, mert mind a szakmai, mind az ismeretterjesztő irodalmat elárasztják a sötét anyagra és sötét energiára hivatkozó híradások. Ez már annyira átitatta a gondolkodást, hogy nehéz ezen rést ütni. Ha valakihez eljut a jelenlegi kozmológiát cáfoló elképzelés, az nem ad hitelt neki, és ösztönösen arra gondol, hogy valami biztosan hibás benne. Ezen nem lehet csodálkozni és bizonyos szempontból nem is baj. Ha ugyanis egy új elmélet megszületik, annak ki kell állni a legszigorúbb kritikát is! Magam is bármilyen kritikát szívesen fogadok, ha megvannak a nyílt vita feltételei. Csak az ellen tiltakozom, ha valaki a tudománytalanság bélyegével áll elő. Végül is mi, vagy ki határozza meg, hogy mi a tudományos és mi tudománytalan? Egy példát hoznék fel. Már száz éve folynak az erőfeszítések, hogy a gravitációt is kvantumos alapokra helyezzék. Ma már ott tartanak, hogy 24 dimenziós láthatatlan térben rezgő húrokat és membránokat tételeznek fel és végtelen számú párhuzamos univerzumról beszélnek, de sajnos még ez sem segít a konzekvens elmélet megtalálásában. Nekem is be kellene állni a sorba, és mondjuk 32 dimenziós láthatatlan tereket kellene elegáns matematikába felöltöztetni, hogy engem is tudományosnak tartsanak? Számomra nem a matematikai öltözet eleganciája a lényeg, hanem az elméleti következtetések és a kísérletek összhangja. Ezt minél egyszerűbb eszközökkel lehet elérni, annál jobb! Bemutattam például, hogy a gravitációs erő relativisztikus korrekciója matematikai bravúrok nélkül is levezethető, ha megtaláljuk a kapcsolatot különböző törvények között. Én ezeknek a kapcsolatoknak megtalálására törekszem, ezt mutattam be előadásomban is.

Köszönöm a figyelmet!