Korábbi bejegyzések 

Előző bejegyzés

A fizika fogalmi rendszerének kialakulása hosszú történetre néz vissza. Először a klasszikus mechanika fogalomrendszere alakult ki, ami a makroszkopikus világból érkező megfigyeléseken alapul. Fordulatot hozott a fizika történetében, amikor eljutott az anyagi világ végső elemeinek feltárásához, viszont ez nem járt együtt a fogalomrendszer új eredményekhez való hozzáigazításával. Ennek az írásnak egyik célja, hogy az anyag elemi objektumai mellé társítsa a fogalmi világ alapvető építőköveit. A modern fizika arra törekszik, hogy felépítse a kölcsönhatások egységes elméletét, ehhez az út a fizika egységes fogalomrendszerén keresztül vezethet. Az írás másik célja, hogy bemutassa azt a törekvést, amely az egységes fizikai fogalomrendszer felépítésére irányul.

A mechanika fogalmai

A fizika fogalomrendszerét nem tudjuk szétválasztani a matematikai fogalmak fejlődésétől. Ennek nagyszerű példája Newton elmélete, aki kéz a kézben fejlesztette tovább a fizikát és a matematikát. Ennek kulcsfontosságú momentuma a folytonosság és az infinitezimális változás precíz megfogalmazása. Induljunk ki a tér és az idő fogalmaiból. A tér az egymásmellettiség világa, az idő az egymásutániságé. Amíg a tér pontja szimmetrikusak a felcserélésre, ez nem teljesül az idő esetén. A térnek nincs kitüntetett előrehaladási iránya, szemben az idővel. Ezt a távolság fogalmával mutathatjuk be. A térbeli távolság nem függ attól, hogy melyik pontból indulunk el a másik felé, ezért a távolságot mindig pozitív érték jellemzi. Amikor a háromdimenziós térben meghatározzuk a P(r’) = P’(x’,y’,z’) = és P(r”) = P”(x”,y”,z”)  pontok távolságát, a komponensek négyzetösszegét képezzük:

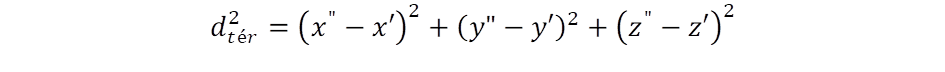
A négyzetes  összefüggés megengedi a negatív értéket is a gyökvonásban, de mi pozitív mennyiségnek tekintjük a távolságot. Az idő dimenziójában az események között eltelt idő fogalmát használjuk, aminek előjel lehet pozitív és negatív is, attól függően, hogy a jelenből a jövő felé, vagy fordítva a múlt felé haladunk. Pozitív, ha t” későbbi idő, mint t’:

d_idő = t” – t’

Ha megfordítjuk t’ és t” sorrendjét negatív értéket kapunk, ami azt fejezi ki, hogy az okozat előtörténetére vagyunk kíváncsiak, vagyis a múlt felé haladunk.

Folytonosság és infinitezimális változás

A térbeli és időbeli távolság nagyságát elvben tetszőlegesen kicsinyre választhatjuk, ez felel meg a tér és idő folytonos szerkezetének. Ez viszont mérésekkel nem ellenőrizhető kijelentés, hiszen a mérési pontosság nem lehet végtelen, ezért extrapolálunk, vagyis átvesszük a matematikából a folytonosság fogalmát, mely szerint a koordinátaváltozás tetszőlegesen kicsiny lehet. Így lép be az infinitezimális változás fogalma a fizikába, és ezen alapul matematikában a függvények differenciálási szabálya. Az egyébként bonyolult fizikai összefüggések az infinitezimális tartományban leegyszerűsödnek, minden összefüggés megfogalmazható egyszerű arányosság formájában. Ezt használta fel Newton is, amikor az erő fogalmát az erő által okozott gyorsulással – azaz az r(t) pályafüggvény idő szerint képzett második differenciálhányadosával kapcsolta össze:

F = m·(d²r(t)/dt²) = m·a

 Az arányossági tényező a tehetetlenség, vagyis a tömeg. A mechanika további fontos fogalma az impulzus (lendület), amit a sebesség és a tömeg szorzata definiál, és megadja, hogy egy mozgó test mekkora lökést gyakorolhat ütközéskor:

p = m·(dr(t)/dt) = m·v

A lökést úgy jellemezhetjük, mint ami megváltoztatva a mozgó test sebességét, illetve impulzusát, és ezáltal az erő szerepét játssza el:  F = dp/dt.

Véges változások

 Az infinitezimális tartományból át kell térni a véges méretű mozgásokra, amikor leírjuk a testek mozgási pályáját. Ennek matematikai eszköze az integrálás, amely által az erőtörvényből kiindulva eljutunk a mozgási pályához. A pálya alapvető jellemzője egy állandó, ami nem változik meg a mozgás során, ez valójában az energia definíciója. Az energiának két összetevője van, egyfelől a potenciális energia, amely létrehozza a mozgást, másfelől a már létrejött mozgáshoz tartozó energia, vagyis a mozgási energia. A kettő összege állandó, ami közvetlenül származtatható a newtoni erőtörvény integrálásával. Ennek konkrét alakja azonban eltér, attól függően, hogy van-e kapcsolat a tér és az idő koordinátái között. A klasszikus mechanika a független leíráson alapul, amely szerint az energia kifejezése a következő:

E = E_kin + E_pot = ½mv² + E_pot = ½p²/m + E_pot

Az E_pot potenciális energia az erőből származtatható az erő által végzett munka kiszámításával, de járható a fordított út is, amikor a térkoordináták szerint deriváljuk a potenciál függvényt, ez a gradiens művelet:

F = –gradE_pot(x,y,z).

A tér és idő összekapcsolódása

 A relativitáselmélet szerint a tér és időkoordináták összekapcsolódnak, ha valamilyen v sebességű rendszerben írjuk le egy test mozgását, ez a Lorentz transzformáció, amely akkor érvényes, ha a megfigyelést állandó v sebességgel mozgó koordinátarendszerben – vagyis inerciarendszerben – végezzük. A kiinduló elv, hogy a c fénysebesség állandó, vagyis független attól, hogy a megfigyelő és a fénykibocsátó objektum között mekkora a v sebesség. Ebből származtatható az invariancia törvény.

Eseménytávolság

Hasonlítsunk össze két „eseményt”, amit a tér és idő koordináták együttese ír le, nevezetesen S(r’, t’) és S(r”, t”). Az eseménytávolság definiálásához alakítsuk át az idő dimenziót térdimenzióvá a c fénysebességgel beszorozva. Ekkor ugyan térdimenzióhoz jutunk, de fennmarad a különbség az eseménypontok felcserélési szabályában, hiszen az idő esetén megfordul a távolság előjele, míg a tér koordináták esetén nem. A többdimenziós távolságképzésekor négyzetre emeljük a koordinátákat, ezért az előjelváltást úgy tudjuk figyelembe venni, ha az időből képzett koordinátát imagináriusnak vesszük, ennek megfelelően a téridő időkoordinátája ic·t lesz.  Viszont a négyzetes összegben a negatív előjelet a térkoordinátáknál alkalmazzuk, mert ez biztosítja, hogy az eseménytávolság valós értékű legyen:

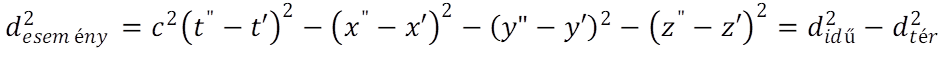
Az így definiált eseménytávolság a téridő struktúrájának invariánsa, ami független a választott referenciarendszer sebességétől. Ez a szabály az alapja az inerciarendszerek ekvivalenciájának. Az invariancia azáltal valósul meg, hogy ha a referencia rendszer sebességét nagyobbnak választjuk, akkor az időbeli és térbeli távolság azonos mértékben csökken. Határesetben, amikor a sebesség a c értékhez tart a tértávolság nulla lesz, és az eseménytávolság megegyezik az időbeli távolsággal. A négyzetes összefüggés megengedi, hogy az eseménytávolság akár pozitív, akár negatív legyen. Ha azt akarjuk kifejezni, hogy az ok megelőzi az okozatot, akkor a pozitív előjelet választhatjuk t’ és t” sorrendjétől függően.

Kovariancia törvény

Koordináta transzformáció szempontjából az x, y, z és t koordináták azonosan viselkednek, mint a ∂/∂x, ∂/∂y, ∂/∂z, ∂/∂t deriváltjaik, és a kvantummechanikai operátor definíció szellemében megfogalmazhatjuk az invariancia szabályt a p_x, p_y, p_z impulzusból és az E energiából felépített négyes vektorra is:

E² = p²c² + m₀²c⁴

Ezt az összefüggést nevezi a fizika kovariancia törvénynek. Ebben az invariánst az m₀ nyugalmi tömeg képviseli. A nyugalmi tömeg tehát az eseménytávolság invarianciájának folyománya. Vezessük be a p₀ = m₀c impulzus dimenziójú mennyiséget, amikor is az

E²/c² = p² + p₀²

kifejezéshez jutunk. Itt a négyzetes összeadási formula már szuggerálja az értelmezést, hogy az energiában két impulzusvektor hatása összegződik, az egyik a külső mozgást írja le, a másik a részecskék saját impulzusa, amely gömbszimmetrikus forgást ír le, és így a külső és belső impulzusok négyzetösszegében a kereszttag átlaga eltűnik.

Nulla tértávolságú mozgások

A mozgás matematikai szempontból a tér és idő koordináták közötti függvénykapcsolat, amiben alapvető szerepet kapnak a differenciálhányadosok. Fizikai szempontból a mozgásokat két típusba soroljuk, a szokásos külső mozgás, amelynek alanya – tehát „ami mozog” – egy másik mozgástípus, amit belső, vagyis elemi mozgásnak nevezhetünk. Ez az elemi mozgás pedig nem más mint az elemi részecskék világa. Ebben a felfogásban úgy értelmezzük az elemi részecskéket, mint egy határértéken történő mozgásformát, amelyben a relativisztikus tértávolság nulla! Ez a fénysebességű mozgások alapelve, mely szerint nincs valamilyen eleve létező anyag a térben, például éter, hanem a téridőnek van egy sajátos mozgási állapota. Ezen elemi mozgásformák által lesz a matematikai térből fizikai tér, vagyis a teret nem tekintjük többé puszta rendezési elvnek, hanem fizikai világunk meghatározó entitásának fogjuk fel. De hogyan válik az elemi mozgás érzékelhető anyaggá, hogy jön létre a tömeg? (Csak megjegyezzük, hogy valójában nem is a tömeg az elemi mozgás legfontosabb jellemzője, az igazán lényeges állapotjellemző az impulzusnyomaték, azaz a spin.)

Tömegnövekedés és tömegteremtés

Mi az eredete a tömegnek? Ennek megértéséhez nyúljunk vissza a kovariancia törvényhez, és alkalmazzuk a tömeg és energia közötti E = m·c² ekvivalencia szabályt, és vezessük be a külső impulzus számára a p = m·v jelölést. Ez elvezet a tömeg sebességfüggéséhez:

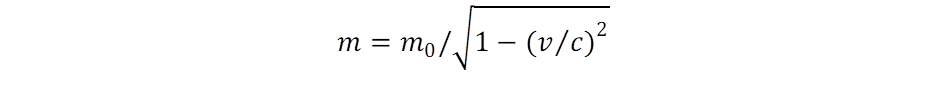
Ennek értelmében a v → c határesetben a tömegnövekedés végtelenhez tart, vagyis a külső mozgás nem érheti el a fény sebességét tömeggel rendelkező objektumok esetén. Más a helyzet a téridő belső mozgásánál, mert ez a tömegmentes tér sajátmozgása! A tömegnélküliség mint nullához tartó határérték fogható fel, amelyet végtelenhez tartó tényezővel szorozva már véges értéket kaphatunk. A kovariancia törvénybe tehát „be van építve” a tömeg létrehozásának lehetősége. De önmagában az csak lehetőség, hogy a fénysebességű mozgás tömeget hozzon létre, ehhez még további feltételnek is teljesülni kell.

A fénysebességű forgásoknak két alaptípusa van, az egyik a körforgás, amit síkforgásnak is nevezhetünk, a másik a gömbforgás, vagy kettősforgás, ami a háromdimenziós tér minden irányán átfut. Az előbbi forgás típus alkotja meg a bozonokat, az utóbbi a fermionokat. A kettősforgással jellemzett fermionoknak már van tömege és töltése is, de ez mire vezethető vissza? A tömeg létrejötthez szükség van egy geometriai feltétel teljesülésére is. Fogalmazzuk ezt meg két elemi fogalommal, az egyik a valahol levés, a másik az összekapcsolódás! A valahol levés azt jelenti, hogy valamilyen fizikai objektum jelöli ki a tér pontjait. Ennek eszköze a gömbszimmetrikus forgás, vagyis a fermion. A gömbszimmetrikus forgás mennyiségi jellemzője a frekvencia, ez határozza meg a tömeget is: annál nehezebb odébb lökni ezt a belső forgást, minél nagyobb annak frekvenciája! A tömeg és frekvencia kapcsolatát a Planck elektromágneses hullámokra megadott összefüggése: E = h·f adja meg, amely összekapcsolható az anyag hullámtermészete miatt az E = m·c² ekvivalencia szabállyal. Az f frekvenciájú forgáshoz tartozik egy r sugár is, ami a gömbforgások c értékű felszíni sebességéből következik: c = 4πr·f. (Figyelem: a térforgás egységsugarú gömbjének felülete 4π, szemben a körforgás 2π kerületével.) Körforgásnál viszont a c = 2πr·f összefüggés határozza meg a sugarat, vagyis a gömbforgás sugara fele lesz a körforgáshoz képest, a felezett sugár pedig feleakkora impulzusnyomatékot ad. Ez fejeződik ki abban, hogy a gömbforgásokkal definiált fermionok spinje S = ½, szemben a körforgással értelmezett S = 1 spinű bozonokkal.

A részecskék mint elemi mozgások

A részecskéket úgy értelmezhetjük mint a tér önfenntartó fénysebességű forgásait. Az előbbiekben már előrevetítettük, hogy a forgásoknak két alaptípusa van, az egyik a körforgás, illetve síkforgás, a másik gömbforgás, azaz térforgás. Az előbbi esetben a részecske síkforgásához tartozik egy helyváltoztató haladó mozgás is, amely történhet akár a forgástengely irányában, de lehet arra merőleges is.

A tömeget úgy értelmezhetjük, mint az objektum ellenállását külső mozgási állapotának fenntartásáért, ennek mértéke a tehetetlenségi erő. Ennek egyik formája a centrifugális erő, ami akkor lép fel, ha a fénysebességű forgás tömeget hoz létre. Viszont az önfenntartó forgás megköveteli, hogy létezzék egy visszatartó erő, ami ellensúlyozza a kifelé ható erőt:

F_cf = m·v²/r = p·v/r

A kifejezésben feltüntettük a p impulzust, hogy beszélhessünk centrifugális erőről akkor is, ha nincs nyugalmi tömeg, de az objektum rendelkezik impulzussal a fotonhoz hasonlóan. Ezt az impulzust Planck, illetve általános estben de Broglie nyomán a p = E/c = h·f/c összefüggés adja meg. Fénysebességű körforgás miatt a sebesség c = 2πr·f = ωr, és bevezetve a ħ = h/2π redukált Planck állandót, a következő kifejezés adja meg a centrifugális erőt:

F_cf = ħ·c/r² = ω²ħ/c

A formulában szerepel a redukált Planck állandó, ami a fénysebességű forgás impulzusnyomatéka. Ez könnyen belátható az impulzus és a forgási sugár szorzatából: p·r = (h·f/c)·(c/2πf) = ħ. A fénysebességű forgás koncepció tehát annak felel meg, hogy a ħ Planck állandó nem csupán a foton energiáját határozza meg, hanem szerepet játszik valamennyi részecske felépítésében. De honnan származik az erő, ami kiegyenlíti a centrifugális erő hatását? Ehhez az általános relativitáselmélet adja meg a kulcsot, amikor a gravitációs erőt a tér görbületére vezeti vissza. De miért görbül a tér a tömeg körül? Erre magyarázatot a Lorentz kontrakció adhat: ha a tömegből gömbszimmetriájú forgás szabadul ki, melynek frekvenciája a Kepler törvény szerint változik, azzal értelmezni tudjuk a gravitációs erő távolságfüggését is. Ebben a szemléletben már nem oka a bolygómozgás törvényének a gravitációs vonzás, hanem megfordul a viszony: a gravitáció származik a forgásokból. Vagyis a forgás az elsődleges, ami megteremti a gravitációs erőt. Alkalmazzuk ezt az elvet a fénysebességű forgásra is! Ekkor a forgási centrumtól r távolságban a kerület nullára csökken, és így létrejön az 1/r²-tel arányos extrém mértékű térgörbület. Az innen származó ħ·c szorzattal jellemzett erőt nevezzük erős gravitációnak, amely két nagyságrenddel haladja meg a töltések közötti Coulomb kölcsönhatást az e² = αħ·c összefüggés szerint, ahol α = 1/137 a Sommerfeld állandó.

Coriolis és Euler erők

A tehetetlenségi erők alapvető szerepet játszanak az egyes kölcsönhatások kiváltásában, ezért vegyük sorra ezeket. Forgó rendszeren belül történő v sebességű mozgásnál egy további tehetetlenségi erő lép fel, ez a Coriolis erő:

F_Coriolis = 2m(vxω) = 2pxω

 A vektoriális szorzat azt fejezi ki, hogy ez a tehetetlenségi erő, akkor lép fel, ha a mozgási irány nem párhuzamos a forgási tengellyel. A fotonok haladó mozgása viszont párhuzamos a tengellyel, vagyis nem lép fel Coriolis erő. Éppen ez a tengellyel párhuzamos terjedési irány biztosítja, hogy a foton előrehaladása állandó frekvenciával és energiával menjen végbe, és a forgási sugár is azonos maradjon. A Coriolis erő hiánya magyarázza, hogy a nulla nyugalmi tömegű fotonnak miért nincs elektromos töltése sem.

Tehetetlenségi erő lép fel akkor is, ha egy külső forgatónyomaték a forgási frekvencia megváltozására kényszeríti az objektumot, ez az Euler erő:

F_Euler = m·rxdω/dt

Az Euler erő a forgási síkban a mindenkori érintő irányában hat.

Összekapcsolódás

A térpontok nem függetlenek egymástól, közöttük erőhatások jönnek létre, ezt fejezzük ki az összekapcsolódás fogalmával. A kapcsolódást elemi forgások hozzák létre, melyek egyrészt fénysebességgel haladnak, másrészt c sebességgel forognak egy tengely körül. Ezek alkotják az elemi részecskék világának másik nagy csoportját, az S = 1 spinű kölcsönhatási bozonokat, amelyek közül már szó volt az elektromágneses kölcsönhatás közvetítőjéről, a fotonról.

A fizikai teret úgy foghatjuk fel, hogy az elemi mozgások által kijelölt pontjait elemi mozgások kapcsolják össze. A térpontok közötti kapcsolódásnak két iránya van, az egyik távolító, a másik közelítő. A távolító erőt nevezzük taszításnak, a közelítőt vonzásnak. Az üres tér, amelyben nincs anyag, vagyis nem léteznek benne elemi mozgások, csupán matematikai fikció, egyszerű rendezési elv. A fizikai tér viszont elemi mozgások összessége, amelyre ráépülnek a külső mozgások. Ezt az elvet képviseli az Einstein által megfogalmazott általános relativitáselmélet is.

Mezőelméletek

Milyen formái léteznek a tér pontjai – azaz az elemi objektumok – közötti kapcsolódásnak. A kérdést úgy vetjük fel, hogy miért éppen négy módja van a kölcsönhatásoknak, és milyen a viszony az egyes kölcsönhatások között? Szólni kell először a mezőelméletekről. De mi is a mező? A mező kölcsönhatási lehetőség. Itt a lehetőség fogalmának különös jelentősége van! Ennek illusztrálására nézzük az elektromos mező eredetét! Ha a térben elhelyezünk egy elektromos töltést, arra a töltéssel arányos erő hat. Ennek arányossági tényezője az elektromos mező. De hogyan épül fel ez a mező? E mögött a töltések összegzett hatása áll. Bármelyik két töltés között fellép a távolság négyzetével csökkenő Coulomb erő, amely lehet vonzás, vagy taszítás a két töltés előjelétől függően. A kölcsönhatásban lévő töltések száma az Avogadro szám (6·10²³) nagyságrendjébe esik. Ennyi kölcsönhatást páronként összegezni lehetetlen, ezért együttes hatásuk leírására vezetjük be a mező (field) fogalmát. Van azonban egy bökkenője a definíciónak! Ha most odateszünk egy további töltést a mező hatásának mérésére, akkor ez a töltés is hozzájárul a mezőhöz, viszont ezáltal a töltés önmagára való hatását is bevisszük a leírásba. Persze mondhatjuk, hogy a töltések óriási száma miatt ez nem okoz gondot. Van viszont egy kivétel, ha a töltés sajátenergiáját akarjuk kiszámítani. Ezt úgy végzik el, hogy gondolatban a töltést apró elemekre bontják és elviszik a végtelenbe, majd a centrumba visszahozva kiszámítják, hogy a Coulomb erővel szemben ez mekkora munkavégzést jelent. Az eredmény végtelen lesz, ez a dilemmája mind a klasszikus, mind a kvantum mezőelméletnek, a kvantumelektrodinamikának. Mit kell kezdeni evvel a végtelennel? Valójában semmit, mert ez a végtelen az elkövetett logikai hiba „büntetése”. Egyrészt az elemi töltést nem lehet felbontani, másrészt a töltés nem hat önmagára, csak a többi töltésre.

Mágneses mező és a reltivitáselmélet

A mozgó töltések között fellép egy retardációs hatás is, amely forgató jellegű, ennek mértékét a v sebesség és a c fénysebesség aránya határozza meg. Ez a mágneses kölcsönhatás, amit az elektrodinamika a mágneses mezővel ír le. Ennek fellépését a retardációs effektus okozza: mivel minden hatás véges c sebességgel terjed, így nem elegendő a térkoordinátákat figyelembe venni két töltés közötti kölcsönhatásban, hiszen a hatás bekövetkeztekor a két részecske pozíciója már megváltozott. Emiatt az elektromágnesesség a négydimenziós téridőben érvényesülő kölcsönhatás. Maxwell korában, aki a klasszikus elektromágneses mezőelmélet végső formáját megalkotta, a relativitáselmélet még nem született meg, ennek ellenére ez a formalizmus már megfelelt a relativitáselmélet invariancia követelményének.

A fény kvantumelmélete: QED

A Maxwell elmélet nagy felismerése, hogy a fény mint elektromágneses hullám írható le, de ebben még a folytonossági elv érvényesült: nem létezett alsó határ egy adott frekvenciájú fény energiájában. Planck korszakalkotó felfedetése, hogy a fény is kvantumos, amelynek egysége a foton. Ez vezetett el az elektromágnesesség kvantumelméletéhez, a kvantumelektrodinamikához (QED), amely a virtuálisan kibocsátott és elnyelt fotonok hatására vezeti vissza az elektromos és a mágneses mezőt. Mivel a foton impulzussal és impulzusnyomatékkal is rendelkezik, ez ide-oda lökődést idéz elő a töltött részecske pozíciójában, és ide-oda perdülést az orientációban, ez hozza létre egyrészt az elektromos, másrészt a mágneses mezőt és ezek fluktuációját, amit kvantumfluktuációnak nevezünk.  A fluktuáció hatása kísérletileg megfigyelhető az anomális mágneses nyomaték értékében és a Lamb shiftben. (itt csak utalunk rá, más írásokban ezt részletesen kifejtésre került).

A fénysebességű forgások koncepciója ezt a képet azzal egészíti ki, hogy fermionok gömbszimmetrikus térforgásában a két forgás viszonya lehet balkéz, illetve jobbkéz szimmetriájú, akárcsak a tér három tengelyének iránya. A háromdimenziós tér kétféle geometriája a kiralitás. A fénysebességű forgásmodellben az egyik felel meg az anyagnak, a másik az antianyagnak. A tehetetlenség és a gravitációs vonzóerő tekintetében nem játszik szerepet a kétféle kiralitás, de annál fontosabb, ha értelmezni akarjuk az annihiláció során bekövetkező tömegeltűnést. Ezért célszerű pozitív tömegről beszélni az anyagnál és negatívról az antianyagnál, hasonlóan ahhoz, hogy pozitív és negatív töltésről beszélünk a részecskék és antirészecske párjuk esetén. A tehetetlenség szempontjából az előjel kettőssége azért nem játszik szerepet, mert a kovariancia törvény szerint (ez a mechanika legáltalánosabb törvénye!) a tömeg négyzete határozza meg az energia kifejezését.

Térjünk vissza az elektromágneses tér és a töltés eredetére. A kettősforgás komponensei között fellép a Coriolis erő, amely periodikusan felborítja az önfenntartó forgás erőegyensúlyát, ami egytengelyű forgások, azaz fotonok kibocsátásához és elnyeléséhez vezet (ezek a virtuális fotonok). A fénysebességű forgások koncepciója tehát nem csupán felhasználja a QED hipotézisét, amikor virtuális fotonokkal magyarázza az elektromágneses kölcsönhatást, hanem annak okát is megadja, hogy miért jön létre a fotonok kibocsátása és elnyelése, vagyis a kvantumfluktuáció.

A virtuális fotonok forgási iránya (polarizációja) kétféle lehet függően a fermion kiralitásától. A foton impulzussal rendelkezik, ami kibocsátáskor visszalöki a fermiont, de ennek iránya attól függ, hogy merre mutat a forgási irány. A kétféle polarizációs irány jelenik meg abban, hogy a töltés lehet pozitív és negatív, vagyis a kölcsönhatás lehet vonzás vagy taszítás. Taszítás jön létre, ha a két töltés előjele, azaz a kiralitás megegyezik, és vonzás az ellenkező esetben. Ha végül feltesszük a kérdést, hogy mi a töltés? A válasz: a fermiont övező virtuális foton felhő, amelyet a folytonosan kilépő és elnyelődő virtuális fotonok tartanak fenn. Ezek impulzusa hozza létre az elektromos, impulzusnyomatéka a mágneses mezőt.

Kvarkfizika, a hármasság világa

Kíséreljük meg, hogy fogalmi rendszerünket kiterjesszük a részecskefizika kvark modelljére is! Ez már teljességgel a virtuális részecskék világa, mert kvarkokat önállóan nem figyelhetünk meg. Létezésükhöz az kell, hogy az erős kölcsönhatás mezonokat és barionokat építsen fel belőlük. Az összetett részecskék közül a legfontosabb a két nukleon, a proton és neutron, ezek alkotják az atommagokat.  A fénysebességű forgás koncepcióban úgy fogalmazhatunk, hogy léteznek egyszerű és összetett kettősforgások. Egyszerű kettősforgás az elektron és családjának tagjai, a müon és a tau részecske, illetve ezek antianyag társa, mint például a pozitron. Ezek mind tiszta királis állapotok és töltésük –e és +e, tömegükhöz pedig pozitív, illetve negatív értéket rendelhetünk az annihiláció értelmezése érdekében. Az összetett kettősforgás viszont kevert királis állapotokat hoz létre, a gyenge kölcsönhatás „csomagolási technikája” egyenlő súlyt ad a két kiralitásnak, ennek eredménye a töltéssemleges és tömeggel nem rendelkező neutrínó. Az erős kölcsönhatás viszont a kettősforgás három szakaszra bontásával hozza létre a kvarkokat, ami törttöltéseket eredményez. A töltés ±⅔e és ±⅓e lehet, az előbbit nevezzük up típusnak (flavour), az utóbbi a down. Az kétféle előjel a részecske-antirészecske kettősségre utal, konkrétan a ⅔e és –⅓e töltésű kvarkokból épül fel a proton (két up és egy down), illetve a neutron (egy up és két down). Amíg a virtuális kvarkok kevert királis állapotok, a két illetve három kvarkból vagy antikvarkból felépülő megfigyelhető részecskék már tiszta királis állapotok, amelyek töltése az elemi töltés egészszámú többszöröse, vagy nulla. Tehát a megfigyelhetőség együtt jár a tiszta kiralitással.

A harmadolási szabály megmutatkozik az erős kölcsönhatás jellegében is. A gravitáció „alanya és tárgya” a tömeg, az elektromágnesességé a töltés, ennek megfelelően az erős kölcsönhatásnak is megvan a maga alanya és tárgya, amit színnek nevezünk. Az „egyarcú” gravitációt a pozitív tömeg, az elektromágnességet a kétarcú töltés (pozitív és negatív) hordozza, addig az erős kölcsönhatás „háromarcú”, amit a három színnek nevezett entitás játszik el. A színekre épülő erős kölcsönhatás elmélete a kromodinamika. Annak analógiájára, hogy az elektromágneses kölcsönhatást az S = 1 spinű fotonok közvetítik, az erős kölcsönhatásban ezt a szerepet a gluonok játsszák el. Ezek feladata a három-három színnel rendelkező kvarkok összekapcsolása. Ez összesen kilenc kombinációt jelent, de ebből egyet, amely totálszimmetrikus, kizár az elmélet, és összesen nyolc különböző gluonról beszél. Az atommagokban a protonokat és neutronokat is az erős kölcsönhatás kovácsolja össze. Ebben a folyamatban a kvarkok kicserélődése játssza el azt a szerepet, mint a molekulákban az elektron, amikor kötést hoz létre atomok között.

De honnan származik a hármasság? A színnek miért pont három arca van? A fénysebességű koncepció alapja, hogy a mozgás az elsőrendű entitás, minden más tulajdonság, legyen szó tömegről, vagy kölcsönhatási erőről, ebből fakad. A kvantumelmélet egyik fontos tanulsága a zérusponti rezgés. Ha működik egy kitéréssel arányos visszatartó erő, mint például molekulákban az egyes atomokat rögzítő kémiai kötés, akkor ez örökös rezgési állapotot (oszcillációt) tart fent még a legalsó energiaszinten is. A kötésben levés és a rezgés elválaszthatatlan. A nukleonok megalkotásában is működik egy kötőerő, az erős kölcsönhatás, ezért a nukleonokban is elválaszthatatlanul jelen van a zérusponti rezgés. A térnek három dimenziója van, mindegyikhez tartozik egy oszcillációs irány. Ez a három oszcilláció formálja meg azt az entitást, amit színnek nevezünk. A mozgás elsőbbségét valló felfogásban ez azt jelenti, hogy elsődlegesen létezik ez a három oszcillációs mozgási állapot, ami kiváltja az erős kölcsönhatást.

A fermionoknak három generációja van, egyszerű kettősforgások esetén az elektron, müon és a tau részecske. Három generáció létezik a kvarkoknál is. A magasabb generáció nagyobb tömeget jelent, vagyis nagyobb forgási frekvenciát, ami egyúttal kisebb saját sugárral jár együtt. Mi magyarázza az egyes frekvenciák értékét, vagy ha úgy tetszik a tömegeket? Erre jelenleg nem tud válaszolni a részecskefizika standard modellje sem.

Spontán és indukált folyamatok

A részecskék állapotának változása két fő típusba sorolható, az egyik az átmenet, a másik az átalakulás. Mindkettő bekövetkezhet spontán módon, de kívülről indukálva is. A spontán átalakulás és átmenet arra utal, hogy az összetett mikro rendszereknek van saját belső történetük is, még ha ezt nem is tudjuk nyomon követni, csak bekövetkezésükhöz valószínűségeket rendelhetünk. Példa rá, amikor az atom nagyobb energiájú (gerjesztett) elektronja spontán módon kisebb energiájú pályára ugrik, vagy, amikor a radioaktív izotópok elbomlanak. Az átalakulásokat elősegíthetjük elektromágneses sugárzással, ez már indukált folyamat, amelyben a tér különböző pontjai közötti kölcsönhatás jelenik meg. Az egyik pont, ahonnan elindulnak a sugarak, a másik, ahol a változás bekövetkezik.

EPR paradoxon

 Itt eljutottunk egy olyan ponthoz, ami számtalan félreértést, paradoxont idéz elő. Felteszik gyakran a kérdést: ha kiválasztunk egy neutront, meg tudjuk-e mondani, hogy mikor fog átalakulni? Csak annyit tudunk mondani, hogy negyedórán belül a neutronok fele fog átalakulni. Hol van a kérdésben a hiba? Ott, hogy csak akkor tudunk egy részecskét „kiválasztani”, ha látjuk, vagy kitapogatjuk. Amíg a neutron nem változik meg, nem ad magáról semmi hírt, vagyis nem látjuk, nem tudjuk „kitapogatni”. A mikrovilág fizikája, a kvantummechanika eleve tudomásul veszi, hogy vannak „láthatatlan” állapotok, ilyen például az elektron stacionárius állapota az atomban. Mivel az atomban nem látjuk az elektron mozgását, tartózkodási esélyéről csak valószínűségi kijelentéseket tehetünk. A kvantummechanika elmélete olyan matematikai módszer, ami elvégzi az esélylatolgatást, és emiatt valószínűségekről beszél az időbeli lefutás, a „pálya” pontos leírása helyett. Éppen ezért a kvantummechanikát nem kell, sőt nem is lehet „rejtett paraméterekkel” kiegészíteni, amiről az EPR paradoxon szól. (Az elnevezés Einstein, Podolsky és Rosen nevére utal, akik felvetették a kvantummechanika kiegészítésének szükségességét.) Az EPR paradoxont úgy kell értelmezni, mint egy logikai hiba „büntetését”.

Kvantumátmenet

Kvantumátmenetről akkor beszélünk, ha egy részecske állapota úgy változik meg, hogy a sajátfrekvenciája (tömege) és töltése ugyanaz marad. Erre példa, amikor az atomban kötött elektron megváltoztatja pályáját, például az L = 1 p pályáról átugrik az L = 0 s pályára (L az elektronpálya impulzusnyomatékának kvantumszáma). Ezt az átalakulást a foton S = 1 spinje közvetíti biztosítva az impulzusnyomaték megmaradását. Hasonló a helyzet, amikor a mágneses mezőben lévő elektron átugrik az S_z = ½ spin polarizációs állapotból az S_z = –½ állapotba. Ugyanilyen átmenetet hoznak létre a spinnel rendelkező atommagok is mágneses mezőben. Az átmenet mindig csak a részecske külső mozgását változtatja meg, de a belső mozgás változatlan marad a spin polarizációs irányától eltekintve.

Részecskeátalakulás és gyenge kölcsönhatás

Az átalakulás már a részecske belső, szerkezeti mozgását változtatja meg, ekkor megváltozik a sajátforgás frekvenciája (tömege), de megváltozhat a töltése is. Az előbbi eset következik be, amikor a müon, vagy tau részecske alakul át elektronná, az utóbbinak felel meg a neutron átalakulása protonná az alfabomlás során. Ehhez az összetett változáshoz már összetett közvetítő mechanizmusra van szükség, amit a gyenge kölcsönhatás elmélete ír le. Ennek főszereplője a W bozon, amely szöges ellentéte a fotonnak, mert van elektromos töltése és tömege is, ráadásul ez a tömeg messze meghaladja valamennyi megfigyelhető fermionét. A nagyon különböző tulajdonságok ellenére a W bozon mégis a foton közeli rokona: ez is egytengelyű forgás összekapcsolódva egy terjedő mozgással, amelynek iránya azonban merőleges a forgási tengelyre, ami pedig a forgási sugár fénysebességű növekedését idézi elő. A sugárnövekedés viszont frekvenciacsökkenéssel, azaz energiavesztéssel jár együtt. A W bozonnak van töltése is, mert a terjedési irány merőleges a forgástengelyre, azaz fellép a Coriolis erő. A töltés előjele lehet pozitív és negatív is a forgás polarizációs iránya szerint.  A tömeg létezését pedig az okozza, hogy a táguló W bozon mozgási centruma helyben marad – ellentétben a fotonnal – vagyis ez a részecske helyhez kötött mozgási állapot. A W bozon tömege valójában indulási, vagy képződési mennyiség. Viszont épp a gyors frekvenciacsökkenés teszi alkalmassá a W bozont, hogy átalakítsa az elemi részecskéket, mert a tágulás során végigpásztázva a rendkívül széles frekvencia skálát bármelyik fermionnal rezonanciába léphet. Erre épp azért van lehetőség, mert a W bozon tömege nagyobb, mint bármely fermioné a részecskefizika Standard Modellje szerint.

A fénysebességű mozgás önfenntartási elve kézenfekvő magyarázatot kínál arra is, hogy a neutron alfabomlásának első fázisában hogyan bocsáthat ki egy nála közel százszor nagyobb tömegű W bozont. Nem sérül ugyanis az energiamegmaradás elve, mert a tömegnek megfelelő energiát ellensúlyozza a térgörbület által létrehozott negatív potenciális energia. A fermiont alkotó kettősforgás a részecskehatáron nem lép túl, vagyis ott a frekvencia nullára csökken, a frekvenciaugrás pedig kiváltja az Euler erőt. Ennek nagysága attól függ, hogy milyen széles az a zóna, amelyben bekövetkezik a frekvencia lecsökkenése. Ez a részecske sugaránál jóval kisebb tartományban valósul meg, ezért nagyobb lesz az Euler erő, mint a fénysebességű kettősforgás ħc/r² nagyságú centrifugális ereje. A centrifugális és Coriolis erővel szemben az Euler erő nem sugár, hanem érintő irányú, amiért az erő által kiléptetett egytengelyű forgáshoz tengelyre merőleges terjedés társul. Ezt a mozgást testesíti meg a W bozon. Mivel a zónaszélesség csak kisebb lehet, mint a részecskesugár, így a kilépő bozon tömege nagyobb lesz, mint a kibocsátást végző fermioné. A kölcsönhatás második fázisában a neutronból (a kvark elméletben a down részecskéből) kilépő S = 1 spinű W^- bozon úgy alakulhat át S = ½ spinű elektronná, ha ennek során egy töltéssemleges neutrínó is létrejön. Ez biztosítja az impulzusnyomaték (spin) megmaradását. A neutrínó töltéssemlegessége annak felel meg, hogy ekkor a kétféle kiralitás egyenlő súllyal van jelen. A kétféle kiralitás egyenlő súlya nem csak a töltést, hanem a tömeget is megszünteti. Ez összhangban van a megfigyeléssel, hogy a neutrínó fénysebességgel mozog. A Napból érkező neutrínók száma elmarad az elméletileg várt értéktől, amit a neutrínó oszcillációval magyaráznak. Ebben feltételezik, hogy a különböző generációjú fermionok átalakulásából származó neutrínók eltérő tömeggel rendelkeznek. Erre a hipotézisre azonban nincs szükség, mert a neutrínó – még ha nem is rendelkezik tömeggel – impulzusa attól még lehet, akár csak a nullatömegű fotonnak. A neutrínó oszcilláció pedig magyarázható az impulzusok különbségével is.

Ahhoz hasonlóan, ahogy a gyenge kölcsönhatás egybecsomagolja a két királis kettősforgást, a kétféle polarizációjú síkforgás is egybeköthető, ez a mozgási állapot a gyenge kölcsönhatás semleges Z bozonja. Az elektrogyenge kölcsönhatás mezőelmélete csokorba köti a fotont és a három gyenge kölcsönhatási bozont (W⁺, W^-, Z), jelentős lépést téve a közös mezőelmélet megalkotása felé. Ennél is továbblép a kromodinamika beillesztése az egységes mezőelméletbe, amelyben már 12 bozon szerepel a 8 gluon felvétele miatt. Egyedül a gravitáció maradt ki a sorból, amit nem sikerült kvantumos alapra helyezni. A kudarc okát abban látom, hogy a feltételezett gravitációt közvetítő graviton nem létezik, sőt szerintem nem is létezhet.

A gravitáció közvetítője: a kepleron

Bár spinnel rendelkező graviton nem létezik, még sincs arról szó, hogy a gravitációnak ne lenne közvetítő mechanizmusa. A fermionból kiléphet a kettősforgás is a tehetetlenségi erők (Coriolis, Euler, centrifugális) kombinációja révén, de a kilépő forgás frekvenciája sok-sok nagyságrenddel lecsökken. Ez azt eredményezi, hogy a részecske határán az extrém görbület nem csökken le teljesen nullára, egy kicsiny térgörbület fennmarad, és ez a távolsággal tovább csökken a Kepler törvénynek megfelelően. A forgás kerületi sebessége a fénysebességtől messze elmarad, de a Lorentz kontrakció révén így is létrejön egy kicsiny térgörbület, ami a szokásos gravitációt eredményezi. A lassú kettősforgások felhőként övezik a fermiont, de ennek a felhőnek nincs tömege, impulzusa és impulzusnyomatéka sem, vagyis nem tekinthető sem bozonnak, sem fermionnak. Ezt a sajátos mozgást nevezzük el Kepler tiszteletére kepleronnak!  Vagyis a fermionokat két felhő veszi körül, az egyiket a virtuális fotonok alkotják, a másik a kepleron felhő. Az előbbinek van impulzusa és impulzusnyomatéka, ezáltal fejti ki hatását, az utóbbi viszont a tér szerkezetét szabja át. A görbületek összeadódnak és bármilyen csekély az egy-egy részecske által okozott görbület, a részecskék hatalmas száma miatt –  bolygó, vagy csillag méretekben – már a gravitációs erő dominanciára tehet szert, és fekete lyukakban még a fényt is foglyul ejtheti.

Oksági lánc és távolhatás

A modern fizika törekvése, hogy minden kölcsönhatást bozonokkal írjon le, mintha elfelejtkezne valamiről, mégpedig a neutrínók egyik fontos funkciójáról. Mielőtt erre rátérnénk térjünk vissza az elektromos kölcsönhatásra!. Valahol a térben, lehet az akár egy távoli csillagban, vagy galaxisban is, egy elektron átugrik egy másik állapotba és kibocsát egy fotont. Itt a Földön, például a szemünkben, egy másik elektron elnyeli ezt a fotont és megváltoztatja állapotát. Miről van tehát szó? Két távoli elektron kerül egymással kölcsönhatásba, ezt oksági láncolatként fogjuk fel, és a fény (foton) fogalmával kötjük össze. Lépjünk tovább! Most egy neutron alakul át valahol, például a Napban, és alfabomlással átalakul protonná miközben kibocsát egy elektront és egy neutrínót. Ez a neutrínó is hosszú útra kel és megérkezve a Földre, egy protont átalakít neutronná. Itt is arról van szó, hogy két részecske, most egy neutron és egy proton, oksági kapcsolatba kerül. Ezt az átalakulást közvetíti a neutrínó. A neutrínó viszont fermion, vagyis a kölcsönhatások közvetítése nem egyedül a bozonok kiváltsága. Miért lenne hát kötelező a gravitációt is bozonok közreműködésének tulajdonítani? Indokolt tehát a törekvés, hogy más típusú elemi mozgást keressünk a gravitáció közvetítésére, így kerül a képbe a kepleron. Másik tanulság, hogy a gyenge kölcsönhatás nem kizárólag rövidtávon működik. Ennek a kölcsönhatásnak ugyanis két arca van, az egyik valóban csak közvetlenül a részecske határon fejti ki hatását, ezt végzi el a W bozon. A másik viszont távolba hat, ezt az átalakítást már egy fermion, a neutrínó hajtja végre.

Összefoglalás

Fizikai világunkat a tér fénysebességű sajátmozgásai építik fel. A tér pontjait gömbszimmetrikus kettősforgások, vagyis fermionok jelölik ki. Ezek önfenntartó mozgások, ahol egyensúlyban van a kifelé ható centrifugális erő és a befelé húzó erős gravitáció, amit a fénysebességgel forgó tér görbülete hoz létre. A fermionok összekapcsolódnak fénysebességgel terjedő mozgások kibocsátása és elnyelése által. A folyamatokat fénysebességgel forgó rendszerben működő tehetetlenségi erők (Coriolis és Euler) idézik elő.

Minden kölcsönhatást valamilyen fénysebességgel terjedő mozgás közvetít, ez bozon az elektromágneses és erős kölcsönhatásban (foton, illetve gluonok), a gyenge kölcsönhatásban egy bozon és egy fermion együttműködése játszik szerepet (W és Z bozon, illetve neutrínó), a gravitációt viszont spinnel nem rendelkező kettősforgások (kepleronok) hozzák létre.

Végül foglaljuk össze, hogy mi az a fizikai entitás, ami kiváltja a kölcsönhatást, és mi az, amire hat:

• A gravitáció alanya és tárgya a tömeg, vagyis a fénysebességű kettősforgás tehetetlensége,
• az elektromágneses kölcsönhatásé a töltés, vagyis a virtuális foton felhő,
• az erős kölcsönhatásé a szín, vagyis a zérusponti rezgés három iránya,
• a gyenge kölcsönhatásé a kettősforgás frekvenciája és kiralitása.

Így valósul meg a mozgás primátusa a fizika világában.