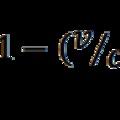Ha valamit nem ismerünk eléggé, akkor segít a képzelet, hogy kitöltsük a hézagokat. De a képzeletbeli fizikai állapotokat olykor összetévesztjük a valóságossal, és ilyenkor felléphetnek ellentmondások is. Erre mutatok be néhány példát a következőkben.

Mikor valódi a pálya?

Akár a kozmikus sugárzás, akár a gyorsítók által nagy energiára szert tett részecskék útját nyomon követhetjük, Erre azért van lehetőségünk, mert a részecskék nyomot hagynak a vizsgálathoz használt eszközeinkben, például az emulzióban, a köd- vagy a buborék kamrában. Az ionizáló sugárzás kémiai reakciókon keresztül válik láthatóvá és rajzolódik ki a pálya. Itt a lényeg a kölcsönhatás, ami a mozgás során helyről-helyre, pillanatról-pillanatra fellép és emiatt a megfigyelt pályát VALÓDI pályának tekinthetjük. Ezek a kölcsönhatások természetesen befolyásolják a pályát, de ettől eltekinthetünk, ha az egyedi kölcsönhatásokhoz tartozó energia sokkal kisebb, mint a részecske kezdeti energiája. Vizsgálhatjuk a pálya görbületét mágneses mezőben, figyelembe vehetjük az elektromos mező hatását is, és ez kulcsot ad számunkra, hogy meghatározzuk a részecske különböző tulajdonságait, így a töltését, tömegét és impulzusnyomatékát (spin) is.

Szintén valódi pályáról beszélhetünk makroszkopikus testek mozgásánál. Kövessük például a teniszlabda mozgását, ahogy ezt a „sasszem” is teszi, amikor vizsgálja, hogy a labda érintette-e a vonalat. A Napból érkező sugarak visszaverődnek a labdáról és eljutnak a videokamerába, amelyik a felvételt készíti. A fénysugarak gyakorlatilag folytonosan érkeznek, és hatásuk nem befolyásolja érdemben a labda pályáját, így jogosan tekintjük a video képet helyesnek a labda mozgásáról.

Mikor képzeletbeli a pálya?

De most ugorjunk egyet és tegyük fel a kérdést, mit tudunk mondani az egyes fotonok pályájáról, amíg a labdától a kamera felvevőjéhez, vagy a szemünkbe jut? Ezt úgy tudhatnánk meg, ha valahol menetközben végeznénk méréseket a foton kibocsátási helye és a detektor között. Ez természetesen kölcsönhatást igényel, amit már a kvantumelv szabályai igazgatnak, ami azt jelenti, hogy a fény impulzusnyomatéka, energiája, impulzusa is nagymértékben megváltozik. A detektálás után már nem ugyanaz a foton folytatja pályáját, azaz a pálya alapvetően más lesz, és így nem beszélhetünk a pályáról abban az értelemben, ahogy azt a részecske emulzióban rögzített nyoma, vagy a labda videokamerával felvett pályaíve esetén megtehetjük. Igazából csak két dolgot állapíthatunk meg a fotonról, az egyik a képződés helye és ideje, a másik az érkezésé. A kettő közötti utat csak képzeletünk tölti ki. Ez a KÉPZELETBELI pálya lehet egy egyenes, ami a kezdő és végpontot összeköti, de rajzolhatunk gömbhullámokat, amelyek szuperpozíciója értelmezi a foton útját Huygens elve szerint, de lehet a kvantumelektrodinamika módszere, amelyben oszcillátorok írják le az egyes fotonokat, de szemléltethetővé tehetjük a fotont a Feynman által bevezetett forgó nyilakkal is. Akármelyik ábrázolást is választjuk, mindegyik csak elképzelésünk egy-egy változata lesz. A fotont tulajdonképpen a tér két különböző helyén lévő elektron állapotának megváltozása definiálja, amikor a d távolságban lévő elektronokat összeköti valamilyen kölcsönhatás. Amit tudhatunk a kölcsönhatásról, hogy t = d/c idő telik el a két elektron állapotváltozása között (c a fénysebesség) és az egyik elektron energiája épp annyival csökkent le, mint amennyivel a másiké nőtt és ugyanezt elmondhatjuk egyéb fizikai jellemzők, így a mágneses kvantumszám változásáról is. Eddig ugyan elektronokról beszéltünk, de bármely más elektromosan töltött részecske állapotváltozása is vezethet fotonok kibocsátásához és elnyeléséhez.

A mezőelmélet foton képe

A kvantumelektrodinamika azonban túllép azon a képen, amely a fotonokat az elektronállapotok változásán keresztül definiálja, amikor mind a fotonokhoz, mind az elektronokhoz oszcillátorokat rendel. A részecskék megkülönböztető jegye a spin, az előbbinél a spin S = 1 (bozon), az utóbbinál S = ½ (fermion). A kétfajta részecske az elméletben egymást kölcsönösen definiálja. A kvantumelektrodinamika ezenkívül nem csak a változás dinamikáját, hanem a kölcsönhatás statikáját is leírja. Ezt úgy végzi el, hogy ez elektromos mezőt VIRTUÁLIS fotonok hatásához rendeli. Ennek legszebb alkalmazása, amikor az elektron anomális mágneses nyomatéka rendkívüli pontossággal kerül meghatározásra. Nincs a fizikában még egy olyan mennyiség, amit ekkora pontossággal ismernénk, és aminek elméleti reprodukálása ennyire pontos lenne. Virtuális fotonokon az elmélet azt érti, hogy ezek a fotonok egyidejűleg képződnek és eltűnnek, és létrehozzák az elektromágneses mező ingadozását a klasszikus fizika által meghatározott érték körül, viszont ezek a fotonok kísérletileg nem detektálhatók. Tehát az elmélet „bevallottan” képzeletbeli fotonok koncepciójára épül.

A valódi és a képzeletbeli pályák fogalmi ütközése

Az elektron anomális mágneses momentumának számolásánál a virtuális fotonok különböző folyamatait veszik alapul, melyeket a Feynman diagramokkal lehet sorba venni. Ilyen például elektron-pozitron párkeltési reakció. Még olyan folyamat is van, amikor egy elektron-pozitron pár előbb fejti ki a hatását, mint amikor létrejön. Szintén vannak olyan folyamatok, ahol a fotonok lokális terjedési sebessége meghaladja a fénysebességet. Zavarba ejtő kép, amely ellentmondani látszik a hétköznapi világból nyert fogalmainknak a térről, időről, az oksági elvről és ráadásul még a relativitáselméletnek is ellentmond. Valójában itt egy gondolati csapdával állunk szembe, aminek oka, hogy nem teszünk különbséget a valóságos folyamatok, a valóságos pályák és az elképzeléseink által alkotott folyamatok és pályák között. Pedig ez a különbségtétel az ellentmondások magyarázatának kulcsa, hiszen a virtuális világban könnyen képzelünk el olyan történéseket, amely ellentmondhat akár az oksági elvnek megengedve a múltba való visszatérést is. Ne gondoljuk azonban, hogy ez a képzeletbeli világ önkényes, vagy szubjektív lenne! Ebben a világban is szigorú törvények uralkodnak: a matematika egzakt szabályai.

Mit értsünk a hullámfüggvény redukciója alatt?

 A valóságos és a képzeletbeli dolgok megkülönböztetésének hiánya vezet el minket a kvantummechanika értelmezési dilemmáihoz is, amire nézzünk meg néhány példát! Az elképzelt jelleg jelenik meg az állapotfüggvény szerkezetében, amelynek abszolút érték négyzete írja le a molekulákban az elektron térbeli valószínűség eloszlását. Ugyancsak az állapotfüggvény határozza meg az egyes fizikai mennyiségek várhatóértékét. Az állapotfüggvény is képzeletünk matematikai terméke, amelynek jogosultságát az adja meg, hogy megadja a mérések lehetséges eredményét és ehhez valószínűséget rendel. Ha azonban elvégzünk egy mérést, az már egy határozott értéket ad meg a lehetséges értékek közül. Ez a megvalósult érték kijelöl egy állapotfüggvényt, amely már nem rendelkezik valószínűségi jelleggel, legalább is az éppen megmért fizikai mennyiség vonatkozásában. Az állapotfüggvénynek ezt a változását nevezi a koppenhágai iskola – amit ma a fizikusok többsége elfogad – a hullámfüggvény redukciójának. Ezt a redukciót azonban nem szabad valódi fizikai folyamatnak felfogni, bár sokan annak tartják, mert csupán arról van szó, hogy a lehetséges és képzeletbeli értékek közül egy kiválasztásra került a mérés során. A koppenhágai iskolának ezt a felfogását ezért a gondolati csapda egyik esetének tartom.

Mi határozza meg az egyedi fotonok sorsát?

Nézzünk meg most egy konkrét esetet. Amikor az üveglapra fényt bocsátunk, a fény 96 százaléka az üveglapon árhalad és 4 százaléka visszaverődik. De hogyan értelmezzük a jelenséget, ha a fényt egyedi fotonok sokaságából építjük fel? Képzeljünk el most egy fotont, amelyik megérkezik az üveglap felületére! Mi lesz a sorsa? Visszaverődik, vagy tovább halad? Kell lenni valamilyen egyedi szabálynak, hogy sok foton esetén a statisztika teljesüljön. Az egyik magyarázat szerint, amit statisztikai koncepciónak neveznek, valójában maga a kérdés rossz, hiszen mindig nagyszámú foton hoz létre detektálható eredményt. A magyarázat gyönge pontja, hogy van lehetőség az egyedi foton sorsának követésére. Legyen két detektorunk, két fotoelektron sokszorozó, ami elég érzékeny ahhoz, hogy képes legyen az egyedi fotonokat észlelni. Az egyik detektor a visszavert, a másik az áthaladó fotont detektálja. A fényforrásunk pedig olyan legyen, hogy csak ritkán bocsát ki egy-egy fotont, amelyek külön-külön adnak jelet. Eben az esetben már nem „gondolatkísérletről” van szó, hanem valódiról és jogunk van arra, hogy rákérdezzünk az egyes fotonok sorsára is!

Einstein gondolatkísérleteinek értelmezése

Vizsgáljuk meg Einstein két gondolatkísérletét! Egy fényforrást detektorokkal veszünk körül és a forrás egyenként bocsát ki fotonokat. Mindig csak az egyik detektor fog megszólalni, de honnan tudja a többi, hogy nekik hallgatni kell? Hasonló a dilemma a kétréses kísérletben, amikor egy zárt gömb van a fényforrás körül két szűk réssel, amin a fény áthaladhat. Ha kívül van egy fényérzékeny lemez, azon interferencia maximumok és minimumok jönnek létre. Sok foton esetén ez a fény hullámtermészetével magyarázható. Ha viszont egyesével indulnak el a fotonok, akkor nagyobb valószínűséggel érkezik meg a foton oda, ahol az interferenciának maximuma van. Az első példát úgy értelmezhetjük, ha a fotont részecskének képzeljük el, amelyik elindul valamilyen irányban és ez az irány jelöli ki, hogy melyik detektor fog megszólalni. A második példában már nem használható a részecske kép, mert az interferencia arra mutat, hogy a foton egyidejűleg áthaladt mind a két résen, ezt pedig csak egy hullám teheti meg, amelyet Huygens elve szerint minden pontban – így a két résen is – létrejövő újabb gömbhullámok szuperpozíciója hoz létre.. Most akkor hullám, vagy részecske a foton, tesszük fel a kérdést, vagy elképzelhető, hogy egyidejűleg mind a kettő? Ez ismét egy gondolkozási csapda, ugyanis arról van szó, hogy a foton pályája csupán képzeletbeli és nem valódi, az elképzelt pálya pedig többféleképp építhető fel. Dilemmánk abból fakad, hogy valóságosnak képzeljük a fantázia szülte képet, amikor a foton pályáját felépítjük. Az tekinthető valódi eseménynek, amikor az első elektron állapota megváltozik, ezt értelmezzük foton kibocsátásnak, utána változik meg egy másik elektron állapota valamelyik detektorban, erre mondjuk, hogy a foton megérkezett és elnyelődött. A két valódi esemény között keressük az oksági kapcsolatot, amit úgy oldunk meg, hogy kitöltjük a két esemény közötti időbeli és térbeli hézagot. Ez a „kitöltés” pedig a foton képzeletbeli pályája.

A fázis szerepe a fotonok reakcióiban

Hátra van még a KIVÁLASZTÁS kérdése: a kibocsátó elektron hogyan határozza meg, hogy melyik detektorban lévő elektron állapotát fogja megváltoztatni? A kvantummechanika erre csak valószínűségi választ ad. Einstein, aki determinisztikus képben gondolkozott a mikrovilág folyamataiban is, felvetette, hogy a kvantummechanika nem teljes, ki kell egészíteni valamilyen rejtett paraméterrel, ami eldönti az egyes események sorsát. Sok vitát kiváltó elképzelését két szerző társával (Podolsky és Rosen) együtt jelentette meg, ami a szakirodalomban az EPR paradoxon elnevezést viseli három szerző nevének kezdőbetűje alapján. Erről részletesen írtam a korábbi bejegyzésekben („Hogyan hozhatunk létre teleportálást a kvantummechanika szerint?”, „Einstein igazsága és tévedései: Gravitációs hullámok és az EPR paradoxon” bejegyzés második része). Itt most azt emelem ki, hogy épp a kiválasztás kérdése miatt nem csupán gondolati konstrukció a foton, hanem rendelkezik önmeghatározó tulajdonsággal is,ez pedig a foton fázisa, amely az energiájával arányos frekvenciával körbejár és meghatározza a pillanatnyi polarizációs irányt. A fázist a foton születésének pillanatában a kibocsátó elektron fázisa szabja meg. Az elektronnak is van fázisa, aminek bizonyítéka, hogy az elektronok között is megfigyelhető interferencia, és ez a fázis a hullámfüggvényben is szerepel, viszont ennek értékét nem tudhatjuk, mert erről nincs előzetes mérési információ. Determinisztikus elképzelésünknek az felel meg, hogyha pontosan ismerjük a kezdő feltételeket, akkor a folyamatok kimenetele is meghatározott lesz. Itt azonban ismét csak egy feltételezés, hogy pontosan ismerjük és képesek vagyunk reprodukálni a kezdő feltételeket, mert a fázist nem ismerjük és az ismeretlen fázis miatt csak valószínűségi kijelentéseket tehetünk a kísérlet kimenetelére. Einstein rejtett paraméterre vonatkozó koncepcióját az alapján cáfolják meg a szakirodalomban, hogyha ez a rejtett paraméter rögzítené a kezdeti polarizációs irányt, akkor olyan összefüggésekhez jutunk, ami ütközik a kvantummechanikai bizonytalansági elvével. De ez a cáfolat is gondolkozási csapda, mert arra a feltételezésre épül, hogy a polarizációs iránynak mérés nélkül is van valóságos értelme. Ez pedig nincs így, mert ha nincsenek fotonok, amelyek kijelölik az irányokat, akkor nincs jogunk irányról sem beszélni a kölcsönhatásban nem levő foton állapotának leírásában. Ugyanakkor Einsteinnek sincs teljesen igaza, mert a folyamatok sorsát eldöntő paraméter nem a kvantummechanikán kívül van, hanem annak szerves tartozéka. Amikor a foton találkozik a detektor egyik elektronjával, akkor nemcsak a rezonancia feltétel határozza meg, hogy okoz-e a foton elektron átmenetet, hanem az is, hogy az elektron állapotának fázisa egyezik-e a foton fázisával.

Kvantált elektronállapotok atomokban

Amikor elektronpályákat rajzolunk fel az atommagok körül szintén képzeletünkre hagyatkozunk. A bolygók pályájáról a Nap körül folytonos információval rendelkezünk, hiszen folytonosan érkeznek hozzánk az onnan visszaverődő fotonok. Az elektronpályákról akkor szerzünk tudomást, amikor az elektron az egyik pályáról egy másikra kerül. Mindig csak ugrásokat látunk, de az állandó, úgynevezett stacionárius pályák rejtve maradnak előlünk. Rajzolhatunk szép ábrákat, amelyben bemutatjuk az egyes pályák eloszlását az állapotfüggvényt meghatározó kvantumszámok alapján. A pálya-impulzusnyomatékot jellemző kvantumszám, ha nulla (s-pálya) akkor gömbszimmetrikus pályát rajzolunk fel, ha L = 1 (p-pálya), akkor a magban összefutó két lebeny tünteti fel az eloszlás alakját, hasonlóan ábrázolhatjuk a magasabb kvantumszámú eloszlásokat is. De az már hibás elképzelés, ha rákérdezünk, hogyan mozog az elektron a pályán belül. Például az L =1 p-pályák az atommagban nulla valószínűséggel fordulnak elő és nem kérdezhetjük meg, hogyan közlekedik az elektron a két lebeny között. Amikor az elektron pályán belüli mozgásáról beszélünk ismét egy gondolkozási csapda rabjai lettünk, mert az elektron pályafogalma is csak képzeletbeli és nem valóságos. A kvantummechanikai valószínűség nem fejez ki többet, mint nem-tudásunkat a valódi pályáról. Az elektron „mozgása” nem a klasszikus tér és idő dimenziókban történik, hanem a térben értelmezett valószínűségi mezőben. Ezt az elképzelést mutattam be egy elképzelt párbeszéddel az elektron és a fizikus között: lásd „Az intelligens elektron” című bejegyzést.

A gondolkozási csapdák elkerülése

A kvantummechanika valószínűség fogalma gyakran teszi próbára logikánkat, amikor a makrovilág fogalmaival akarunk valamit megérteni. Ilyenkor a legjobb, ha elgondolkozunk rajta, hogy a vizsgált jelenségből mi az, ami valódi, azaz tényleges megfigyeléseken alapul,és mi az amit képzeletünk, vagy matematikánk tesz hozzá, hogy összekösse a megfigyeléseken alapuló fogalmaink között tátongó hézagokat..Ha elválasztjuk egymástól a valódi és a képzeletbeli fizikai világot, akkor esélyünk van rá, hogy ellentmondásmentes világképet alkossunk.

A blog egyéb írásait összegzi és megadja a linkeket a „Paradigmaváltás a fizikában” című bejegyzés