A fénysebesség és a Planck állandó a tér szerkezeti állandói

Amikor az elemi részecskék tulajdonságait és kölcsönhatásait kutatjuk valójában a téridő szerkezetét tárjuk fel. Véges univerzumunkban minden véges, ez vonatkozik a kölcsönhatások sebességére is, ennek határát a c fénysebesség jelöli ki, ami a téridő egyik legfontosabb szerkezeti állandója. Ez a határsebesség hozza létre forgások formájában a részecskék világát és határozza meg a speciális relativitáselmélet mozgástörvényeit. Ezek a törvények viszont arra vezetnek, hogy a fénysebességű forgások extrém mértékben görbítik a teret, mert olyan körpályákat hoznak létre, ahol az r sugárhoz tatozó kör kerülete nulla lesz. A görbült térhez potenciális energia és centripetális erő tartozik, amely fenntartja az elemi, azaz fénysebességű forgásokat a centrifugális erő ellensúlyozásával. Ez a görbületi erő, amit erős gravitációnak neveztem el, a téridő egy második szerkezeti állandójától függ, a ℏ= h/2π Planck-állandótól: F_cp = ℏ.c/r². Az univerzum egységes és ebben a téridő homogén, ami szerint c és ℏ mindenütt azonos, nem csak a Földön, a Naprendszerben, a Tejútrendszerben, hanem a távoli galaxisokban is, és emiatt lesz azonos valamennyi elemi részecske bárhol is legyen.

A foton fénysebességű mozgásai

A részecskék közül egyedül a foton rendelkezik avval a tulajdonsággal, hogy energiája tetszőleges lehet. A foton egytengelyű forgás, amely egyidejűleg a forgástengely irányában szintén fénysebességgel halad és a forgás frekvenciája tetszőleges lehet. Ez az ω = 2π.ν frekvencia határozza meg a foton energiáját E = h. ν  = ℏ.ω  , illetve impulzusát P = h. ν/c összefüggések szerint. Az erős gravitáció kifejezéséből az is következik, hogy a foton impulzusnyomatéka  I = ℏ független a foton frekvenciájától, ennek felel meg a foton S = 1 spinje, ami a Planck állandó együtthatója az impulzusnyomaték kifejezésében.

Az elektron sajátforgásai : a fénysebességű kettős forgás

A fotont S = 1 spinje miatt mint bozont kategorizálja a részecske fizika. Ezzel szemben azok a részecskék, mint az elektron, pozitron, neutrínó, proton fele akkora impulzusnyomatékkal rendelkeznek, azaz S = ½ a spin, a fermionok osztályába tartoznak. A spin feleződését avval magyarázzuk, hogy ezek a részecskék kettős forgást végeznek, egyfelől ugyanúgy fénysebességgel forognak, mint a foton, de ekkor a forgástengely is forog és a két forgás együtt egy gömbfelületen történik. A kettősforgás megduplázza a centrifugális erőt, amit csak úgy tud kompenzálni a tér görbületi ereje, hogy fele akkora impulzusnyomatékot hoz létre. Szemben a fotonnal, amelyik fénysebességgel halad és ezért nem lokalizálható egyetlen pontban és emiatt nem is beszélhetünk nyugalmi tömegről, a fermionok gömbje kijelöl egy matematikai pontot, ami már lokalizálja a tömeget is. További eltérés a fotonhoz képest, hogy a két forgás miatt fellép egy tehetetlenségi erő, amit Coriolis erőnek hívunk, ez egy csavaró hatást hoz létre, melynek nagysága szintén F_Coriolis = ℏ.c/r², viszont a csavaró hatásnak két iránya lehet, attól függően, hogy a két forgás hogyan csatlakozik egymáshoz képest. Ezt a két lehetőséget a jobb- és balkéz szimmetriájához rendelhetjük, amit egyébként kiralitásnak nevezünk. Foton esetén ez a tehetetlenségi erő nem lép fel, mert ott a forgás tengelye és a haladás iránya párhuzamos. Ez magyarázza, hogy a foton nem rendelkezik elektromos töltéssel szemben az elektronnal és a pozitronnal. Az elektront tekintjük anyagnak, a pozitront antianyagnak, ami annak felel meg, hogy az egyik részecske jobbkéz, a másik balkéz szimmetriával rendelkezik. A Coriolis erő két ellentétes csavarási iránya okozza, hogy ez elektromos töltés előjele ellentétes az elektron és a pozitron esetén.

A téridő négy dimenziójának kapcsolata a fizikai mennyiségeket meghatározó három dimenzióval

Fizikai dimenziókról két értelemben szokás beszélni, az egyik a téridő négy dimenziója (háromdimenziós tér plusz az idő), a másik a fizikai mennyiségek három dimenziója: a hossz, az idő és a tömeg. A kétféle dimenziós elv között természetes kapcsolatot teremt a fénysebességű mozgásokon alapuló részecskemodell, ami a téridő-részecske fogalomhoz vezet. Mivel kétféle fénysebességű mozgás szükséges a részecskék felépítéséhez ez két térdimenzió elvesztését jelenti, ami azonban létre hoz egy újat, a tömeget. Így alakul át a téridő négy dimenziója a részecskék saját tulajdonságait leíró három dimenzióvá.

A részecskék mint a tér rezonanciái

A dimenziók természetes alapegységéül a téridő állandói választhatók, így a c fénysebesség és a h Planck állandó, de hiányzik a harmadik természetes állandó. Erre legesélyesebb az elektron tömege, mert ez az egyetlen olyan stabilis részecske, amelyik nem összetett, mint a proton, hanem valóban eleminek tekinthető. Felmerül a kérdés, hogy szemben az egytengelyű forgásokkal, tehát a fotonokkal, ahol tetszőleges forgási frekvencia megengedett a kétdimenziós forgások miért csak diszkrét értékeket vehetnek fel, ami elektron és pozitron esetén 0,511 MeV, a vele hasonló tulajdonságú μ  (müon) és τ  (tauon) részecskék esetén 105,7 MeV, illetve 1777 MeV nyugalmi energiának felel meg. Az utóbbi két részecske azonban nem stabilis 2,2.10^-6 s illetve 3.10^-13 s felezési idővel bomlik el a gyenge kölcsönhatás mechanizmusában, miközben elektronok és a semleges neutrínók képződnek. Az említett részecske család, amit a szakirodalom a leptonok közé sorol, úgy képződik, hogy a kettős forgás során a kétféle forgás rezonanciába kerül. Az alaprezonancia hozza létre az elektront, a magasabb frekvenciájú rezonanciák a müonnak és tauonnak felelnek meg. Az utóbbiak tehát az elektron gerjesztett állapotai. Jelenlegi elméleti modellek, például a Standard Modell nem ad választ arra, hogy miért pont ekkorák a részecske tömegek, illetve rezonancia frekvenciák, ezért csak annyit mondhatunk, hogy ez a téridő még feltáratlan szerkezeti tulajdonsága. Még az is kérdéses, hogy csak ez a három rezonanciaállapot (generáció) létezik, vagy lehet-e egy nagyobb energiájú (3000 MeV fölötti) és még rövidebb (például 10^-20 s) felezési idejű gerjesztett állapot is. A jelenlegi elméleti modellek más részecskecsaládokban, így a neutrínóknál és kvarkoknál sem látják szükségesnek a negyedik generáció létezését, de ennek lehetősége ott is megvan.

A kölcsönhatások csatolási állandói

A tér szerkezetéről nyerünk információt a különböző kölcsönhatások alapján. Két hosszú távú kölcsönhatás létezik, az egyik a gravitáció, a másik az elektromágneses. Közös bennük, hogy az erőhatások a távolság négyzetével csökkennek és mindkettőre a c sebességű terjedés vonatkozik. Ebből arra következtethetünk, hogy mindkét esetben a részecske saját mozgása által perturbálja a környezetét valamilyen „külső” mozgás indukálásával, ami aztán gömbszerűen terjed a térben és azért gyengül, mert a forrástól távolodva nagyobb felületen oszlik el és így az erő a sugár négyzetével arányosan lecsökken.

Az elektromágneses kölcsönhatás kvantumelmélete

Az elektromágneses kölcsönhatásra kvantumelektrodinamika jó leírást ad, aminek lényege a részecske körül az elektromágneses mező létrehozása virtuális fotonok kibocsátása és elnyelése révén. (A virtualitás azt jelenti, hogy ezeket a fotonokat közvetlenül nem „látjuk”, viszont hatásuk hozza létre az elektromos mezőt.) A kibocsátások és elnyelések dinamikus egyensúlya biztosítja az erőmező statikus jellegét, azonban ennek értéke ingadozik az átlagérték körül. Ezt a jelenséget nevezik vákuumingadozásnak. Az elmélet legfontosabb sikere, hogy az ingadozás révén lehetett magyarázatot adni két fontos kísérleti megfigyelésre, az egyik az elektron anomális mágneses nyomatéka, a másik a Lamb shift. Az utóbbi jelenség bizonyos degenerált (azonos értékű) elektron nívók felhasadását magyarázza, ami még a relativisztikus Dirac egyenlet szerint is azonos energiájú. A mágneses nyomaték anomáliája azt jelenti, hogy a kísérletileg meghatározott érték eltér a Dirac egyenlet alapján várttól. Az elmélet összhangban van a fénysebességű forgásmodellel, mert az elektromos mező arányos a kettősforgás Coriolis erejével: E = αℏ.c/r²  (Itt a szimbólum vastagítása jelzi, hogy nem energiáról van szó!). Az elektromos mező kifejezésében az  α = 1/137 a Sommerfeld féle finom-kölcsönhatási állandó úgy értelmezhető, mint a kettősforgás és az egytengelyű forgás csatolási állandója, mely szerint a csavaró erőnek csak egy kis hányada hoz létre, vagy nyel el egytengelyű forgásokat, azaz virtuális fotonokat. Miért pont ekkora az állandó? Erre nincs elfogadott magyarázat, ezt is úgy tekinthetjük mint a tér szerkezeti állandóját, ami meghatározza két különböző mozgásforma csatolódását. Az elektromágneses kölcsönhatás kvantumos, mert a virtuális fotonok is rendelkeznek S = 1 spinnel, ami a kvantum alapja.

A gravitációs kölcsönhatás és a Kepler forgások

Az elektromágneses kölcsönhatásnál még azt kell kiemelni, hogy nem függ a részecske tömegétől, azaz a sajátforgás frekvenciájától. Ebben a tekintetben nagy a különbség a tömegvonzáshoz képest, amelynek ereje arányos az m tömeggel, tehát a részecske ω sajátfrekvenciájával. Ezt úgy értelmezzük, hogy a tömeg –  tehát a kettősforgás – a részecske környezetében lassú frekvenciájú kettős forgásokat gerjeszt, amelynek frekvenciája a Kepler törvény szerint változik, azaz γ.m = Ω²R³, ahol  γ az általános gravitációs állandó, Ω a keringés frekvenciája és R a sugara. Kiindulva ebből a feltevésből és számításba véve, hogy ez a keringés mennyivel csökkenti a pálya kerületét a speciális relativitás elmélete szerint, majd ez alapján definiáljuk a tér görbületét, ami aztán elvezet Newton tömegvonzási törvényéhez (Lásd a korábbi bejegyzésekben: „Fénysebességű forgások és a relativitáselmélet”). Ez az elgondolás alátámasztja, hogy a részecske sajátforgása valóban úgy perturbálja környezetét, hogy kialakulnak a tömeg körül a lassú Kepler forgások. Fejezzük ki a részecske tömegét a sajátfrekvenciával: m = ℏω/c² és rendezzük át az egyenletet:

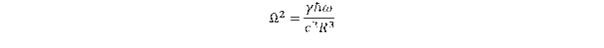
A kifejezésben szereplő γℏ/c² a gravitációs kölcsönhatás csatolási állandója, ez a tér egy további szerkezeti állandója, aminek értékére nincs elméleti magyarázat. A Kepler forgás frekvenciájának négyzete arányos a részecske saját frekvenciájával. Mivel a görbület Ω² –tel arányos, így mindig pozitív lesz, ezért a gravitációs hatás összeadódik függetlenül a részecske kiralitásától. Ez is különbséget jelent az elektromágneses kölcsönhatáshoz képest, ahol vonzó és taszító kölcsönhatás egyaránt lehet. Nullához tartó sugár esetén a Kepler frekvencia végtelen lenne, de ez nem fordulhat elő, mert a Kepler forgások a részecskén kívüli tartományban jönnek létre. Nézzük meg, hogy mekkora lesz a Kepler frekvencia közvetlenül a részecske felületén, amikor R = r = c/ω? Az eredmény:

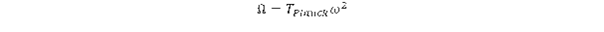
ahol a Planck idő definíciója:

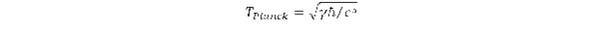
A Planck idő rendkívül rövid (~10^-43 s), ezért a Kepler frekvencia és a hozzá tartozó kerületi sebesség annyival kisebb a fénysebességnél, hogy a részecskéből kilépő tartományban a relativisztikus rövidülés elhanyagolható. Mivel a tömeg létrejöttét a fénysebességű mozgás idézi elő a Kepler forgáshoz nem rendelhető tömeg és emiatt impulzusnyomaték sem. Spin hiányában viszont ezek a forgások nem kvantumosak. Ez magyarázza, hogy miért nem lehet a gravitációra kvantumelméletet alkotni.

Mi közvetíti a térben a gravitációs hatást?

Összevetve az elektromágneses és a gravitációs hatást kiváltó mechanizmust, az előbbire világos magyarázatot ad a kettősforgás Coriolis ereje, amely útjára indítja a virtuális fotonokat, de milyen erő okozhatja a szintén fénysebességgel terjedő gravitációs hatást? A szokásos fizikai közegekben, vízben vagy a levegőben, ha egy lokális forgás, azaz örvény jön létre, az környezetében hullámokat vet, de ebben az esetben a közeget alkotó objektumok ütközése hozza létre azt a kölcsönhatást, amely közvetíti a hullámok terjedését. Ilyenkor beszélhetünk a közeg viszkozitásáról, de jogos-e feltételezni hasonlót a vákuumban? A fénysebességű kettősforgás tartományának határfelületén – azaz az r = c/ω  sugárnál – a felület nulla, azon kívül, ha nem lenne Kepler forgás azonnal 4r²π   értékre ugrana fel a felszín, tehát egy végtelenül éles ugrás következne be a tér szerkezetében. Matematikailag ez egy szakadást jelentene a felszín sugártól való függésében. Ez már egy kvantumos ugrást jelent, ami realizálódik is az elektromágneses kölcsönhatásban, ami elvezet a kvantumelektrodinamika formalizmusához. A gravitáció viszont folytonosságot követel meg, nincsenek kvantumai. Ez abban nyilvánul meg, hogy a határon való átlépés függvénye kissé „lekerekedik”, a felszín sugártól való függése differenciálhatóvá válik. Másképp fogalmazva: a tér szerkezete nem engedi meg a végtelenül éles ugrásokat, az ugrás élességének is van egy felső határa. Ez a határ a tér szerkezeti tulajdonsága, aminek mértékét a γ gravitációs állandó határozza meg. A forgási frekvencia szempontjából ez úgy mutatkozik meg, hogy az ω sajátfrekvencia az r = c/ω  határt átlépve nem nullára esik le, hanem az Ω  Kepler frekvenciára, amelynek nagysága a Planck idővel megadott mértékben kapcsolódik a sajátforgás frekvenciájának négyzetéhez. Ez a forgás virtuális, hasonlóan az elektromágneses kölcsönhatást közvetítő fotonok virtualitásához, szerepe hogy a térben továbbterjedve felépítse a teljes gravitációs mezőt.

Az erős kölcsönhatás és a tér görbülete

A tér görbületének folytonossága a részecskék környezetében nem csak azt követeli meg, hogy a görbület ne nullára essen le, hanem azt is, hogy az átmenet folytonos legyen. A felszín szempontjából ez azt jelenti, hogy a részecske nulla felszíne fokozatosan veszi fel a 4r²π értéket egy nagyon keskeny átmeneti tartományban..Ennek megnyilvánulása kvarkok esetén, hogy ezek a részecskék nem rendelkeznek határozott tömeggel és ennek megfelelően a sugár nagysága sem meghatározott. A sugár határozatlansága pedig a térgörbület határozatlanságát hozza magával. Ez a görbületi eloszlás lesz a kvantumos  és rövidtávon ható erős kölcsönhatás forrása.  A folytonosság elve elektronok és pozitronok esetén a kvantumelektrodinamika által bevezetett vákuumingadozásban jelenik meg, amely térgörbületi eloszlást hoz létre a részecskék határán.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.