Fénysebességű forgások és a relativitáselmélet:
A Dirac-egyenlettől az általános fermion egyenletig
Rockenbauer Antal
A részecskefizika nyitott kérdései I és II címen már ismertettem a fermionok sajátmozgásaira adott elképzeléseimet, ebben az írásban a modell mélyebb kvantummechanikai alapjait mutatom be.
A relativitáselmélettel összhangban levő kvantummechanikát Dirac alkotta meg. Ez a tudományos eredmény Maxwell teljesítményéhez mérhető, aki az elektromágnesesség alapegyenleteinek felírása által eljutott a fény természetének megértéséhez, Dirac sikeresen kapcsolta össze a két modern fizikai elméletet, előre megjósolta a pozitron – és általában az anti-részecskék – létezését és szilárd alapokra helyezte az elemi részecskék saját impulzusmomentumának, a spinnek fogalmát. A következőkben bemutatom, hogy a részecskék fénysebességű forgásán alapuló elképzelés hogyan helyezi új megvilágításba a speciális relativitás elméletét és hogyan teszi lehetővé a Dirac-egyenletet kiterjesztését az elemi fermionok leírására.
Nézzük meg először a fénysebességű forgások kapcsolatát a relativitáselmélet transzformációs törvényeivel.
Sajátforgás és Lorentz-invariancia
A speciális relativitás elméletében az energia négyzetesen tevődik össze két komponensből, az egyik a részecske impulzusából származik, ez a relativisztikus kinetikus energia: Ekin =p.c, a másik a nyugalmi energia Erest = moc2
E2 = E2kin + E2rest = c2.p2 + m20.c4
Mint látható a nyugalmi tömeggel rendelkező részecskék esetén kvadratikus reláció áll fent az energia két összetevője között. Ilyen összegzési szabály akkor várható, ha vektorokat adunk össze és a vektorkomponensek merőlegesek egymásra és így közöttük a skalárisszorzat eltűnik. A relativisztikus kinetikus energia vektoriális eredete az impulzus vektor jellegéből következik, de hogyan kapcsolhatjuk a nyugalmi energiát is valamilyen vektorhoz? Erre a kérdésre választ ad az elképzelésünk, mely szerint a nyugalmi energia valójában fénysebességű forgásoktól származik (lásd „A részecskefizika nyitott kérdései I és II” című blogot), és ezáltal a részecske rendelkezik saját impulzussal és impulzusmomentummal.
Az elemi részecskéket két alaptípusba sorolhatjuk attól függően, hogy rendelkeznek-e nyugalmi tömeggel. Itt most két részecske fajtát emelünk ki: a zérus nyugalmi tömegű fotont, melyhez S = 1 spin rendelhető hozzá az egytengelyű forgás miatt, és a nyugalmi tömeggel rendelkező S = 1/2 spinű fermionokat (elektron, pozitron, proton, neutron), ahol a spin a részecskét létrehozó kettős forgásra vezethető vissza. A foton nulla nyugalmi tömege okozza, hogy az E = p.c összefüggés szerint közvetlen kapcsolat van az energia és impulzus között.
Alap feltevésünk, hogy az energia és az impulzus közötti E = p.c összefüggés minden részecskére igaz, ha figyelembe vesszük a részecskék sajátforgását is. Ennek értelmében mind az energiához, mind az impulzushoz a külső térben történő mozgásokon kívül a sajátmozgásokat is figyelembe kell venni. Kimutatjuk, hogy a teljes impulzus és az energia között ez a kapcsolat megköveteli a sajátforgásoknak fénysebességét, és ekvivalens elvnek tekinthető a speciális relativitáselmélet transzformációs törvényeivel.
Fordítsuk meg Dirac eredeti gondolatmenetét, aki a relativisztikus egyenleteket vitte át a kvantummechanika területére, ehelyett jellemezzük a részecske mozgását kvantummechanikai állapotfüggvénnyel és ennek segítségével fogalmazzuk meg a relativisztikus invariancia törvényeit. Eszerint, ha a részecske rendelkezik nyugalmi tömeggel, ezt annak tulajdonítjuk, hogy létezik egy p0 impulzussal járó sajátmozgás, amely hozzáadódik a szokásos transzlációs vagy orbitális p1 impulzushoz [1]:
p = p1 + p0
Izotróp sajátforgást feltételezve a p0 impulzusvektor valamennyi orientációt egyenlő valószínűséggel vesz fel, azaz a részecske sajátmozgását leíró Ψ(r0) állapotfüggvénnyel képzett < p0> várhatóérték nulla lesz. Ugyanakkor az impulzus négyzetének várható értéke – amely meghatározza a nyugalmi energiát – véges értéket vesz fel: p20 = <p20>. Mivel a p0 vektor várhatóértéke nulla így a p1-el alkotott szorzat várható értéke eltűnik, következésképp az E2 = c2p2 összefüggés két négyzetes kifejezés összegére bomlik fel
E2 = c2(p21 + p20)
ahol p0 = m0. c. Itt behelyettesítve az energia és impulzus operátorokat és az egyenletet átrendezve eljutunk a relativisztikus invariancia differenciális alakjához: 
Minthogy a téridő koordináták transzformációja lineáris, így a differenciális alakból következik az integrális alak invarianciája is, azaz
c2.t2 – x2 – y2 – z2 = állandó
Tehát abból a két feltevésből kiindulva, hogy egyrészt az energia kifejezhető az impulzus és a fénysebesség szorzatával, másrészt a részecske sajátforgása izotróp, arra a következtetésre jutunk, hogy a részecske mozgását leíró mozgásegyenletek a Lorentz-transzformációval írhatók le. A nyugalmi energia és a spin izotróp sajátforgásra való visszavezetése, illetve a koordináta transzformációk Lorentz-invarianciája úgy értelmezhető, mint a speciális relativitás elvének két ekvivalens megfogalmazása.
Az energia és tömeg ekvivalencia törvényét E = m.c2 összekapcsolva az E = p.c részecske definícióval az impulzus p = m.c szorzattal adható meg, azaz minden részecske impulzusa a tömeg és a fénysebesség szorzata. A relativitáselmélet sebességekre vonatkozó szabálya szerint a c sebességű rendszerben az u sebességgel mozgó részecske teljes ebessége is c-vel lesz egyenlő. Ez vonatkozik a fénysebességgel forgó részecske sajátrendszerére is, amiért az impulzus kifejezésében a c szorzó lép fel. Ugyanakkor a külső rendszer u sebessége a relativisztikusan megnövekedett tömegen keresztül jelenik meg. Az E = p.c szabály ezért akkor érvényes, ha a részecske valóban a fény sebességével forog!
Az elektron relativisztikus egyenlete elektromágneses térben
Az elektromágneses erőtérben mozgó elektron energiáját a Φ(r) skalár potenciál, és az A(r) vektor potenciál segítségével adhatjuk meg, az előbbi a skaláris energiához, az utóbbi a vektoriális impulzushoz ad járulékot:
(E – e.Φ(r))2 = (c.p – e.A(r))2 + m20.c4
Ide behelyettesítve az energia és az impulzus operátorát jutunk el a Klein-Gordon egyenlethez, amelyben az okoz nehézséget, hogy az energia kvadratikus, amiért a sajátérték egyenlet nem oldható meg a szokásos módon. Az állapotfüggvény meghatározásához ugyanis az energiában lineáris HΨ = EΨ alakú differenciálegyenletre van szükség, amit a Klein-Gordon egyenletből négyzetgyökvonással hozhatunk létre. Dirac korszakalkotó ötlete volt, hogy ezt a gyökvonást mátrixfelbontással oldotta meg.
Az egyenlet valójában négy a spinorok (a vektor és β skalár [2]) által csatolt differenciálegyenlet, amit külön hangsúlyozni akarunk a négydimenziós I egységmátrix feltüntetésével a skalár potenciál kifejezésében:
HD = c.a.(p – e.A(r)) + β.m0.c2 + I.e.Φ(r)
Írjuk fel a Dirac-spinorokat a Pauli-mátrixok direktszorzataival [3]:
HD = c.σx●σ (p – e.A(r)) + σz●I.m0.c2 + I●I.e.Φ(r)
A tényezők sorrendje alapján definiáljuk a különböző Pauli-mátrixok szerepét, illetve azt a teret, ahol hatásukat kifejtik. A direkt szorzat első tényezője az impulzus tagban σx, a nyugalmi energiát adó kifejezésben σz. Mivel a Pauli-mátrixnak két sajátértéke van, nevezetesen +1 és -1, és ezek alkotják a diagonális σz két elemét, így a tömeg előjele lehet egyaránt pozitív és negatív. Az impulzus tagban a diagonális elemeket nem tartalmazó σx szerepel, ami azt jelenti, hogy ebben a 2x2 dimenziós reprezentációban a kinetikus energia csak nem-diagonális elemeket ad, ami – amint a sajátérték egyenlet megoldásából látható – visszaadja a relativitáselmélet tömegnövekedési formuláját [4]. Mindezt úgy is megfogalmazhatjuk, hogy az elektron olyan részecske, amelynek van saját tömege – a nyugalmi tömeg – ami független az inercia rendszer megválasztásától, de nincs saját impulzusa, mert ennek értéke a választott inercia rendszer sebességétől függ. A HD Dirac-operátorban az impulzustól származó diagonális mátrixelemek nullák, ami avval ekvivalens a részecskéket fénysebességű forgásokkal értelmező modellben, hogy a részecske sajátforgása izotróp és így az impulzus átlagértéke nulla. A Coulomb-kölcsönhatást leíró tag első tényezője az egységmátrix, ami azt jelenti, hogy ez a kölcsönhatás független a tömeg előjelétől és a részecske sebességétől.
A direktszorzatokkal felírt Dirac-egyenletben a második helyen álló tényező a spint, azaz az elektron saját impulzusmomentumát definiálja:
S = ½ σ
Ez a tényező az impulzus tagban lép fel. Emiatt a spin járulékot ad az energiához, ha az elektron pályamozgást végez (spin-pálya csatolás), vagy ha mágneses tér hat rá (Zeeman-kölcsönhatás). A nyugalmi energia és a Coulomb-kölcsönhatás viszont nem függ a spintől, amit a szorzat második tényezőjeként feltüntetett egységmátrix mutat.
Megjegyzések
[1 ] A félkövér betűk jelölik a vektoriális mennyiségeket.
[2] Négy darab 4x4 dimenziós mátrix reprezentálja a spinorokat, ebből hármat jelöl az α vektor és egyet a β skalár spinor, ahol az aláhúzás jelöli a mátrix jelleget. A spinorok szorzata anti-szimmetrikus:
αi.αj = - αj.αi
továbbá
αi.β = - β.αi
[3] A három σ Pauli-mátrix 2x2 elemből épül fel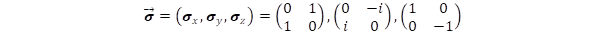
A Pauli-mátrixok nem kommutálnak és szorzatuk anti-szimmetrikus hasonlóan az α spinorokhoz.
A Pauli-mátrixok ● szimbólummal jelölt szorzatai (direkt szorzat) építik fel a 4x4-es spinorokat. Ez a művelet a 2x2-es mátrixok mind a négy elemét egymással szorozva hoz létre 4x4 alakú mátrixokat és
és 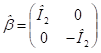
Ebben a kifejezésben I a kétdimenziós egységmátrixot jelöli: 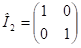
[4] Írjuk fel a Dirac-operátort az elektromágneses mező nélküli esetben és hagyjuk el a direktszorzat második tényezőjét (ezt megtehetjük, ha az u sebességű mozgás irányában vesszük fel a z tengelyt):
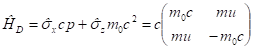
A sajátérték egyenlet a mátrix szekuláris egyenletéből képződik:
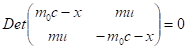
Folytatás a "Fénysebességű forgások_II blogban.
A blog további begyzéseinek összefoglalóját lásd "Paradigmaváltás a fizikában"



