Barangolás a kvarkok és elemi részecskék világában

Evvel az írással kettős célom van. Egyrészt a Standard Modell alapján bemutatom, hogyan lehet felépíteni az összetett részecskéket a kvarkkoncepció alapján, másrészt túllépve a jelenlegi elmélet keretein kísérletet teszek a részecskék karakterisztikus paraméterének, a tömegüknek új módon való meghatározására.

A részecskék osztályozási szempontjai

Az atomot alkotó protonokon, neutronokon és elektronokon kívül a kozmikus sugárzásban és a nagy energiájú ütközéses kísérletekben számos egyéb részecske figyelhető meg. Az elsőleges osztályozási szempont a részecskék spinje, ami ha egészszám, akkor bozonokról, ha félegész – konkrétan  ½ és 3/2  – akkor fermionokról beszélünk. A másik fontos osztályozási szempont a részecske töltése, ami valamennyi esetben az elektron, illetve a proton töltésének egészszámú többszöröse, vagy nulla. Az újabb és újabb részecskék megfigyelése, ami már száz fölött jár, felvetette az igényt további osztályozási elvek kidolgozására. Ennek során Murray Gell-Mann 1964-ben felvetett egy rendkívül szokatlan hipotézist, amikor feltételezte a kísérletileg megfigyelhetetlen törttöltésű részecskék létezését, amit később kvarkoknak nevezett el az irodalom. Ennek értelmében az elemi részecskék többsége nem is „elemi” hanem felbontható két, illetve három kvarkra. Az új osztályozás a fermionok közül csak az elektront, a müont, a tau részecskét és neutrínókat tartja valódi elemi részecskéknek, továbbá a kölcsönhatást közvetítő bozonokat, nevezetesen az elektromágnesesség esetén a fotont, a gyenge és erős nukleáris kölcsönhatásokban a W, Z bozonokat illetve a gluonokat. A modell szerint az összetett bozonokat egy kvark és egy antikvark, míg a fermionokat vagy három kvark, vagy három antikvark alkotja. Az előbbi részecsketípust nevezik mezonoknak, az utóbbit barionoknak, de szokás a két típust együtt hadronoknak nevezni.  A valódi elemi részecskék közé sorolják a müon mezont is, mert tulajdonságai – a tömeg kivételével az elektronéval egyeznek meg –  ezért a jelenlegi nevezéktan szerint ezt már az elektronnal és a hasonló tulajdonságú tau részecskével, valamint a neutrínók három típusával együtt leptonoknak nevezik.

Mi tette szükségessé a kvarkelméletet?

A kvarkok tulajdonságaival már két írásban is foglalkoztunk („A Dirac egyenlettől az általános fermion egyenletig” és ” Nyomozás a sötét anyag után”).  Itt most tekintsük át, hogyan juthatunk el a törttöltésű részecskék feltételezéséhez.  Ehhez támaszkodnunk kell a spinek és a töltések összegzési szabályaira. Kiindulópontunk szerint a kvarkok s =  ½ spinű fermionok, mert ezt követeli meg az izotróp szimmetria (Lásd: „The origin of covariance in the special relativity”). Ebből már adódik, hogy az S = 0 vagy 1 spinű mezonokhoz páros számú, az S = ½ vagy 3/2 spinű barionokhoz páratlan számú összetevő kvarkra van szükség. Az eddig megfigyelt mezonok és barionok esetén elegendő két illetve három kvarkot feltételezni. (Friss hír: a nagy energiájú LHC kísérletekben találtak öt kvark együttesére utaló részecskét, ami úgy értelmezhető mint egy összeépült mezon és barion, de ez a következő gondolatmenetet  nem érinti).  A mezonok töltése lehet nulla, +e és –e, a barionok töltése ezen kívül még felveheti a +2e és –2e értéket is. A lényeg, hogy 2e töltésű mezont, illetve 3e töltésű bariont nem lehetett megfigyelni. A q = ±½e töltés ugyan felépíthetné a mezonokat, de nem magyarázná meg a barionok töltését. Három kvark együttese viszont csak úgy adhat egészszámú töltést, ha az egyedi kvarktöltés az e/3 harmadolt elemi töltés többszöröse, pontosabban szólva q = ±⅓e és ±⅔e lehet, mert az ennél nagyobb töltés esetén az eredő részecsketöltés meghaladná a megfigyelt maximális értékeket. Ekkor viszont a két kvarkból felépülő mezonoknál az egész töltés létrejötte megkívánja, hogy egy kvark és egy antikvarkból épüljön fel (a kvark és antikvark csak a töltés előjelében különbözik), míg a három komponensű barionok  vagy három kvarkból, vagy három antikvarkból állnak össze.  A kvarkoknak két alaptípusa van (erre szokás a flavor szót használni): az up és a down, amit röviden u és d szimbólummal jelölünk. Az előbbi töltése ⅔e pozitív elemi töltés, az utóbbié –⅓e. Minden kvarknak van antirészecske párja, az anti-up, azaz u és anti-down, azaz d, amelyek töltése      –⅔e és ⅓e. A kvarktöltések előjele  a proton +e töltéséből származik, amit az elmélet két u és egy d kvarkkal értelmez, amikor is:  2*⅔e – ⅓e = e. A neutron zérus töltése egy u és két d töltéséből adódik össze, hiszen ekkor ⅔e – 2*⅓e = 0. Az antirészecskék töltésének előjele épp fordított, ami tehát az összetevő kvarkokra is érvényes. A részecskék nagy száma annak a következménye, hogy a kvarkoknak három generációja létezik, amelyek egymással tetszőleges módon kombinálódhatnak.

Mekkora a kvarkok tömege: a renormálási eljárás

A kvarkokkal csak egy baj van: nem lehet őket megfigyelni, azaz nincs szabad kvark, kizárólag mint a hadronok alkotórészei léteznek, legalább is a tudomány mai állása szerint.  Ebből adódik, hogy nyugalmi tömegükre is csak becsléseket lehet adni az úgynevezett renormálási eljárás keretében. A Standard Modell három generációra osztja fel az elemi részecskék családját, ez vonatkozik a kvarkokra is. A család magasabb generációit a nagyobb nyugalmi tömeg különbözteti meg az u és d kvarkoktól, a +2/3e töltésű u típusba tartozik a második generációs charm (c) és a harmadik generációs top (t), míg a -1/3e töltésű d típusba a strange (s) illetve a bottom (b). Közvetlenül nem lehet megfigyelni egyik kvarkot sem (a top kvark ráadásul nem is létezik kötött állapotban rövid élettartama miatt, csak nagy energiájú bomlási reakciókból lehet létezésére következtetni), ezért a kvarkok tömegét különböző mezonok és barionok tömegének összehasonlításával lehet meghatározni. A módszer bizonytalansága, hogy nincs garancia arra, hogy két hadron tömegkülönbsége azonos az alkotó kvarkok tömegkülönbségével, mert a tömeghez járulékot ad az erős, a gyenge és az elektromágneses kölcsönhatás potenciális energiája és ezen kívül a komponensek kinetikus energiája is, ami különbözhet az egyes részecskékben.

A renormálási eljárás újragondolása a relativitáselmélet alapján

A részecskék fénysebességű forgására alapított modellünkben a töltést a részecske kettős forgásának kiralitásához rendeljük, de hogyan fér össze ez a kép a törttöltések létezésével? Itt a kvantummechanikai szuperpozíció elvére lehet támaszkodni: a kvarkok két különböző kiralitású héj szuperpozíciójából épülnek fel (Lásd „A Dirac egyenlettől az általános fermion egyenletig”). Ebből a felfogásból következik a tömeg újraértelmezése is. A relativisztikus kovariancia elv szerint fénysebességű mozgások esetén az energia nem lineárisan tevődik össze a kinetikus és nyugalmi energiából , hanem négyzetesen, ahogy egy derékszögű háromszögben az átló hosszát számoljuk ki a két befogó négyzetéből (Pitagorász tétel). Ezt a négyzetes összegzési szabályt fogjuk alkalmazni összetett részecskékben, amikor az egyes kvarkok tömegét összeadjuk. Áttekintve a mezonok és barionok táblázatát 16 olyan párt lehet találni, amelyek csak egy vagy két d és u típusú kvarkban különböznek. Korábbi bejegyzésünkben („Nyomozás a sötét anyag után) kimutattuk, hogy az ilyen párokban a tömegkülönbség fordítva arányos a részecskék tömegével, ami mutatja a négyzetes összegzési szabály helyességét.

A kvarkok kicserélődési kölcsönhatása

Egy másik törvényszerűség, amit számításba veszünk, hogyan változik meg az azonos kvark összetételű részecske tömege a spin multiplicitás függvényében. Az s = ½  spinek összegzési szabálya szerint a két kvarkot tartalmazó mezonok spinje S = 0 (pszeudoskaláris mezon) vagy S = 1 (vektor mezon) lehet. Két azonos pályán tartózkodó elektron kölcsönhatása esetén az S = 1 triplett és az S = 0 szingulett spin állapotok szeparációját a Heisenberg-féle kicserélődési energia adja meg: H_exch = J.S₁.S₂. Ekkor az S eredő spinhez tartozó energia: E__S = J(S(S+1) – 3/2)/2, ami azt jelenti, hogy a triplett-szingulett szeparáció J-vel egyenlő. A hadronokban kötött kvarkok esetén az extrém relativisztikus körülmények miatt az energia tagok négyzetes összegzési szabálya érvényes, ezért a triplett-szingulett szeparációból számolható kicserélődési energiára

 összefüggést várhatunk. Ennek ellenőrzésére összehasonlítjuk a triplett-szingulett szeparációból számolható J értékeket a lineáris és a négyzetes szabály esetén. Összesen hét olyan lényegesen különböző esetet találtunk a mezonok esetén, ahol az összevetés elvégezhető.  A táblázatból jól látható, hogy a négyzetes szabállyal számolva  J értéke nem függ a mezonok tömegétől és átlagértékben J = 770 MeV lesz.

1. Táblázat: A triplett-szingulett szeparáció függése a mezonok tömegétől a lineáris és négyzetes addíció esetén

A kvarkok energiafüggése a spin multiplicitástól fordított Hund szabálynak engedelmeskedik. Elektron konfigurációkban az azonos spin állapotú részecskék között, amikor a spin maximális értéket vesz fel a kicserélődési kölcsönhatás csökkenti a taszító erőt, ezzel szemben a kvarkok között az erős kölcsönhatás vonzást hoz létre, aminek erősségét csökkenti a nagy spinű állapotban a kvarkok közötti kicserélődési energia. Ennek tulajdoníthatjuk, hogy mezonok esetén, és mint látni fogjuk barionoknál is, mindig a nagy spinű állapot rendelkezik nagyobb energiával.

Kvarkok kicserélődési energiája barionokban

Barionokban a három s = ½ spin eredője S = ½ és S = 3/2 lehet az impulzusmomentum összegzési szabálya szerint, az előbbit nevezzük dublett, az utóbbit kvartett barionoknak. A kvartett barionok azonosítása során kiderült, hogy van olyan részecske is, amelyik három azonos kvarkból épül fel, erre példa a Δ⁺⁺ (uuu) részecske. Ennek a részecskének a létezése fontos szerepet játszott a kvarkelmélet kidolgozásában. Mivel a kvark s = 1/2 spinű fermion, így csak két lehetséges spin állapota van, következésképp a Pauli-elv nem engedi meg a feltételezett uuu konfigurációt, hiszen ekkor legalább két fermion azonos állapotba kerülne. Ezért a Pauli-elv kvarkokra való kiterjesztése miatt szükség volt egy új kvantumszámra, amit szín-kvantumszámnak neveztek el és ez a +1, 0 és -1 értékeket veszi fel. Ez a kvantumszám azonban kizárólag a kvarkoknál jelentkezik, míg a belőlük képzett hadronoknál nem. Ez úgy értelmezhető, hogy a kvarkok három különböző állapotban lehetnek, és a szín-kvantumszámok összege nulla lesz, amikor a hadronok képződnek, hiszen ekkor  1 + 0 -1 = 0. Ezt hozták párhuzamba a színekkel, ahol a három alapszín összeolvadása  „fehér” lesz.  Innen származik a kvantumszám elnevezése. Mezonoknál ez annak felel meg, hogy az antikvark mindig a hozzá kapcsolt kvark komplementer színével rendelkezik, míg barionokban a három kvark színe egymástól különbözni fog. A kvark konfigurációk szempontjából ennek az a következménye, hogy ha három azonos kvarkból épül fel a barion, akkor kizárólag S = 3/2 kvartett spin állapot jöhet létre, ha a három kvarkból kettő azonos, akkor a kvartetten kívül lesz egy S = ½ dublett is, míg ha a három kvark eltérő, akkor a kvartett mellett két különböző S = ½ dublett is lesz.

Hasonlítsuk össze a lineáris és négyzetes összegzési szabály hatását a dublett-dublett szeparáció esetén, ami akkor jön létre, ha három különböző típusú kvarkból épül fel a barion.

2. Táblázat: A dublett barionok energia különbsége a lineáris és négyzetes összegzési szabályok esetén

Csupán négy olyan kvark konfiguráció van, ahol az összehasonlítás elvégezhető. Mindkét számításban növekszik a szeparáció a részecskék tömegével, de a négyzetes szabály esetén ez jelentősebb, ekkor a tömeggel arányosan változik a szeparáció, amit a 2. táblázat utolsó oszlopa mutat. A kvark kicserélődési energia  H_exch = J(S₁.S₂+S₁.S₃+S₂.S₃), ha megegyezik a spin-spin csatolás a barion három kvark-kvark párjában, ebben az esetben a két eredő spin dublett energiája egyenlő lesz. A megfigyelt jelentős dublett-dublett szeparáció ezért arra mutat, hogy aszimmetrikussá válik a három kvark kölcsönhatása – például az egyik pár csatolása jóval erősebb a másik két párhoz képest – és következésképp szétválik a két dublett energiája. A tömeg függvényében növekvő szeparációt úgy értelmezhetjük, hogy az aszimmetria növekszik, amikor a „domináns” kvark (az elsőben s, a második és harmadikban c, a negyedikben b) tömege egyre jobban meghaladja a másik két kvarkét.

Hasonlítsuk össze a kvartett állapot energiáját a dublettel, (ha kettő van,akkor a felsővel), amit a következő táblázat mutat.  Az első példa mutatja a delta részecskék viszonyát a két nukleonnal, tehát a protonnal és a neutronnal. Ezek a barionok a két „alap” kvarkból, tehát u és d kombinációkból épülnek fel. A neutron és proton tömegének a kis különbsége, valamint a négy lehetséges delta részecske (uuu, uud, udd és ddd) tömegének egyezése a kísérleti hiba határán belül, arra mutat, hogy az u és d kvarkok tömege kismértékben különbözik, és az uu, ud iletve dd típusú kvarkok közötti csatolás megegyezik. A korábbi bejegyzésben (Nyomozás a sötét anyag után) azt a kérdést vizsgáltuk, hogy mekkora azoknak a kvark konfigurációknak a tömegkülönbsége, amelyek csak abban különböznek, hogy egy u kvark helyett egy d kvark szerepel.  Ekkor is azt találtuk, hogy a négyzetes összeadási szabály értelmezi helyesen a szeparáció tömegtől való függését. Az összevetés alapján meghatároztuk a két kvark tömegének különbségét , de a kettő összegére nem kaptunk felvilágosítást. Ezt majd a mezonok segítségével fogjuk meghatározni. Előbb azonban vizsgáljuk meg a kvartett- dublett szeparáció változását a lineáris és a négyzetes összegzési szabály esetén.

3. Táblázat: Barion kvartettek és dublettek energiája és szeparációja a lineáris és négyzetes összegzési szabályok alapján

A táblázatból látható, hogy az energiaszeparáció a lineáris modellben nagymértékben csökken a nehezebb barionoknál, míg a négyzetes szabály nem vezet ilyen trendhez. Barionokban az értékek szórása nagyobb, mint amit a mezonok esetén láttunk, de az átlagérték 703 MeV, meglehetősen közel van a mezonoknál tapasztalt 770 MeV értékhez.  Ez a megfigyelés is alátámasztja, hogy a négyzetes összegzési szabály jól adja vissza a tömegek változási szabályát.

A mezonok tömege

A fentiekben vázolt tendenciák segítségével eljárást javasolunk a hadronok tömegének származtatására a kvarkok renormálási tömegei, a közöttük fellépő kicserélődési energia, valamint a kölcsönhatási mező járulékai alapján. Ennek érdekében feltételezünk egy valamennyi hadron esetén alkalmazható összefüggést. Ennek célja, hogy előre lehessen jelezni mekkora a várható tömege a standard modellből következő, de eddig nem detektált részecskéknek. Először a mezonokat vizsgáljuk meg, ami alapján megadhatjuk az öt kvark renormálási tömegét és a kölcsönhatási mező energiajárulékát.

A mezonok családjának legstabilabb és legkisebb tömegű tagja az u kvark és d antikvarkból felépülő pion részecske (π⁺: 140 MeV, π⁰: 135 MeV), amelynek töltéssel rendelkező tagja különösen hosszú életű (10**^-8 s). A nagy stabilitás oka, hogy ez a részecske kizárólag a gyenge kölcsönhatáson keresztül bomlik, szemben az olyan mechanizmusokkal, amiben a gammasugárzás játszik domináns szerepet. A pionok fontos szerepet játszottak az erős kölcsönhatás értelmezésében, hiszen Yukawa javaslata szerint ezek közvetítik a nukleonok közötti erős kölcsönhatást. Ezt arra alapozta, hogy a kölcsönhatás rövid hatótávolsága jó összhangban van a pionok tömegével. A kvarkelmélet kidolgozása azonban más alapokra helyezte az erős kölcsönhatást, amit a szín-kvantumszám kombinációkkal definiált gluonok közvetítenek a kvarkok között, a nukleonok közötti vonzóerőt pedig a gluonok által létrehozott kölcsönhatás polarizációs effektusaként értelmezik. A pionok tömege közel van az u és a d kvarkok négyzetes szabály alapján számított tömegeinek különbségéhez, ezért kiindulópontunk az a feltevés, hogy a pionok tömegét alapvetően a két összetevő kvark renormálási tömege határozza meg. Más szóval ebben a részecskében a különböző energiajárulékok kompenzálják egymást. Ez alapján kapjuk, hogy az u kvark tömege 61 MeV, míg a d kvarké 122 MeV.

Az 5 kvarkból és 5 antikvarkból összesen 2x5x5 = 50 mezon építhető fel, ha az S = 0 és S = 1 mezonokat egyaránt számításba vesszük. A top kvark nem szerepel a számításokban, mert gyors bomlása miatt nem alkot megfigyelhető mezont és bariont.  Összesen 29 mezonra található eltérő nagyságú tömegadat, melyekben a pionok és a szintén u és d kvarkból felépülő triplett mezonok (ρ⁺ és ρ⁰) mellett vannak s, c és b kvarkokat is tartalmazó részecskék: η, K, D, B,ω, φ, ψ, y, ahol a töltésre, spinre és a domináns kvarkra utaló indexek adnak útbaigazítást az összetételről. A töltéssel rendelkező mezonoknak van antirészecske párja is, amelyeknek a tömege azonos a megfelelő részecskével. Egyetlen olyan triplett mezon van (cb összetételű), amelynek nem határozták meg a tömegét, tehát csaknem az összes mezont már sikerült detektálni.

A 29 mezon tömegét a következő összefüggés alapján számítjuk::

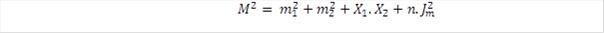
Itt m₁ és m₂ a két kvark renormálási tömege, X₁ és X₂ a két kvark mezőjáruléka, n = 0 a pseudoskaláris és n = 1 a triplett mezonok esetében, J_m = 761 MeV pedig a triplett-szingulett szeparáció. Az X_i mezőjárulék fejezi ki a kölcsönhatási mező és a kötési energiák hatását a mezonok tömegére. A 29 mezon tömege alapján illesztjük az 5 renormálási tömeget és a 3 nullától különböző X_i  mezőjárulékot (az u és d kvarkoknál ezt nullának vesszük), amit még kiegészít a J érték, összesen tehát 9 paramétert illesztünk a 29 tömegadat felhasználásával, ami lehetővé teszi, hogy a nyert paraméterek elég megbízhatóak legyenek, a számított és mért tömegadatok egyezése pedig jelzést ad az alkalmazott eljárás helyességére is.  Ez utóbbit mutatja, hogy a számított értékek hibája minden mezonnál 2 százalék alatt van, a relatív hibák szórása pedig 0,84 %. Létezik azonban két olyan η mezon, melyekre nem alkalmazható a fenti formula. Ugyanis a standard modell valamennyi hadront egy-egy kvark konfigurációval ad meg, kivéve a két η mezont, amit két különböző kvark kombináció szuperpozíciójaként azonosít, ahol az egyik ss típus, a másik u és d kvarkból, illetve antikvarkból tevődik össze. A formulát az ss típusra alkalmazva olyan tömeget kapunk (695 MeV), amely épp a két említett mezon tömege közé esik. Megjegyezzük, hogy az egyetlen hiányzó cb típusú triplett mezonra a számítás 6334 MeV tömeget ad, ezért érdemes lehet a nagyenergiájú kísérletekben ezt az energiatartományt vizsgálni a hiányzó részecske azonosítása érdekében.

Az illesztési eljárással kapott renormálási tömegeket, az X_i mezőjárulékot és a később tárgyalt barionok Y_i mezőjárulékait a 4. Táblázat mutatja:

4. Táblázat: A kvarkok renormálási tömege és mezőjárulékai MeV egységben

A barionok tömege

A 4. táblázatból látható, hogy az általunk számított renormálási tömegek jóval nagyobbak, mint amit a Standard Modell alapján meghatároztak a lineáris összegzési szabály alapján. A különbség különösen nagy a két „alap kvark”, azaz u és d esetében. Az irodalmi értékek szerint csupán 1 százalékot tesz ki a nukleonok tömegéből a renormálási tömeg, míg esetünkben a renormálási tömegek mintegy 20 százalékát adják a részecske tömegének.

A kvark modell összesen 75 barion felépítését teszi lehetővé, amiből 35 a kvartett és 40 a dublett, viszont 16-16 ilyen részecskét nem sikerült megfigyelni, ezért jelenleg 43 részecske tömegadata ismert. A barionok elnevezésére a proton (p) és neutron (n) mellett a Λ, Σ, Ξ, Ω szimbólumokat használják és az indexek utalnak a töltésre, spinre és a kvarkösszetételre. Barionok esetén a következő formulát javasoljuk a tömegek meghatározására:

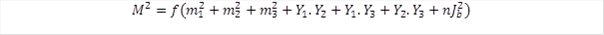
Itt az m_i renormálási tömegek azonosak a mezonok segítségével meghatározott értékekkel. Az f együtthatóval vesszük figyelembe, hogy a két dublett kvark konfigurációban a tömegkülönbség arányos a teljes részecske tömeggel, az illesztési eljárásban  f = 0,976 az alsó és f = 1 a felső dublett esetén. Az Y_i mezőjárulékok határozzák meg, hogy mennyivel kell kiegészíteni a renormálási tömegeket az egyes kvark konfigurációkban és J_b = 742 MeV a kvartett-dublett szeparáció, ennek együtthatója n =1 a kvartett és n = 0 a dublett barionok esetén. Ez összesen 7 újabb paraméter illesztését jelenti a 43 tömegadat felhasználásával, tehát ismét lehetőség nyílik az alkalmazott eljárás helyességének ellenőrzésére. Az illesztéskor kapott Y_i értékek a 4. táblázatban szerepelnek. Az illesztés jóságát mutatja, hogy a legnagyobb relatív eltérés a 43 barion esetén csak 2,7 %, a relatív hibák szórása pedig 1,53 %. Ez a hiba lényegesen kisebb, mint amit lineáris összegzés esetén lehet kapni. Az eljárással meg lehet határozni a 16-16 ismeretlen barion tömegét is. A legnagyobb tömeg a bbb konfigurációjú kvartett bariontól várható: 12980 MeV. 

Összefoglalás

Összegzésként megállapíthatjuk, hogy a speciális relativitáselmélet kovariáns energia formulája alapján feltételezett négyzetes összegzési szabály valamennyi hadron esetén jól alkalmazható a részecskék tömegének meghatározására, ami jó alapot teremt az eddig nem detektált részecskék azonosítására is. A kvarkok renormálási tömege viszont lényegesen nagyobb, mint amekkorát a Standard Modell javasol az energiatagok lineáris összegzése alapján.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.