A Proxima b Centauri Földhöz hasonló tulajdonságai

Nagy port kavart fel a tudományos felfedezés, hogy a hozzánk legközelebbi csillagrendszer egyik csillaga, a Proxima Centauri körül kering egy föld-típusú kőzetbolygó, ami a Proxima b elnevezést kapta. Az izgalomra az adott okot, hogy ez a bolygó olyan távolságban kering a napjától, hogy az onnan érkező sugárzás valószínűleg olyan hőmérsékletet hozhat létre a bolygó felszínén, ami közel lehet a földi viszonyokhoz. Ez a távolság ugyan húszszor kisebb, mint a Föld-Nap távolság, de ez a nap a vörös törpék családjába tartozik, amiért az onnan érkező sugárzás intenzitása sokkal gyengébb, mint a mi napunké. Természetesen még nagyon keveset tudunk erről a bolygóról, nem tudjuk, hogy van-e légköre, vannak-e tengerei, ami alapvető az életfeltételekhez. Ami a felszíni gravitációt illeti, az közel lehet a Földön megszokotthoz, mert a bolygó tömege 1,3-szorosa a Földhöz képest és ha kőzetbolygóról van szó, akkor a sugara is közel lehet a mi bolygónkhoz. Annyit tudunk még, hogy ott egy év nagyon rövid, mert 11,2 nap alatt keringi körül saját csillagát, forgásáról, azaz napjai hosszáról még nem tudunk semmit. Központi csillagának tömegét tudjuk a Newton-Kepler törvény alapján, mely szerint ez a tömeg R³/T²-el arányos, ahol az előbbi a keringési sugár, a másik a keringési idő. Számításba véve, hogy az előbbi 20-szor, az utóbbi 32,6-szor rövidebb, mint a Földé, azt kapjuk, hogy a Proxima Centauri tömege a Nap 13,3 százaléka.

Milyen sugárzás éri a Proxima b Centauri felszínét?

Az élet lehetősége szempontjából fontos a bolygóra érkező sugárzás összetétele. Vörös törpéről van szó, azaz a csillag felszíni hőmérséklete jóval alacsonyabb, mint a Napé, és a fekete test sugárzás törvényéből tudjuk, hogy ekkor a látható, az UV és a még nagyobb frekvenciájú sugárzás részaránya jóval kisebb a vöröshöz képest. Ez annyiból jó, hogy a csillaghoz való kis távolság ellenére az ártalmas sugárzásmennyisége is kisebb lehet, de problémát jelenthet a látható tartományba kevesebb fény jut. A Föld történetéből tudjuk, hogy oxigénben gazdag légkörünket a növények, algák, egysejtűek fotoszintézisének köszönhetjük. Kérdés, hogy ha ez a sugárzási tartomány nem elég intenzív, akkor megvalósulhatott-e a fotoszintézis és így számíthatunk-e oxigénben dús légkörre.

Mennyi üzemanyag kell, hogy elérjük a Proxima b Centaurit űrhajóval?

De legyünk optimisták és induljunk ki abból, hogy megvannak az élet feltételei ezen a ’második Földön’. Ekkor érdemes újragondolni, hogy van-e lehetőségünk arra, hogy eljussunk oda. A sci-fik világában ez nem okoz problémát, az űrhajók vígan röpködnek a csillagok között, csak hát ekkor nem veszik számításba, hogy mennyi és milyen üzemanyag szükséges ezekhez az űrutazásokhoz. Korábbi bejegyzésben („Hogyan látogathatjuk meg a legközelebbi csillagokat”) már végeztem egy becslést, hogy mennyi üzemanyag kellene, hogy megtegyünk az Alfa Centaurira egy körutat. Az volt a konklúzió, hogy a szükséges üzemanyag mennyisége, még antianyag reaktor esetén is rendkívül nagy nem beszélve a kockázatokról. Kicsit jobb a helyzet, ha megelégszünk az oda úttal és nem kell magunkkal vinni üzemanyagot a visszatéréshez is. Ez messze nem felezését jelenti a szükséges üzemanyagnak, mert a megteendő út függvényében exponenciális a növekedés.

Az űrutazás élettani feltételei

A számítás kiindulópontja, hogy az élettani feltételek miatt a hosszan tartó és a földi gravitációt nagymértékben meghaladó gyorsulás nem viselhető el. Másrészt a célba érkezéskor az űrhajót le kell lassítani, mert egyébként vagy óriási sebességgel becsapódna a bolygó felszínébe, vagy elrohanna mellette. Ezért a rakétatechnika, vagy lézersugaras indítás nem alkalmazható. Élettani szempontból az ’1 g’ gyorsulás az optimális, mert ekkor a földihez hasonló gravitációt érezhetünk. Lehetséges a gyorsuló szakaszok váltogatása egyenletes sebességű szakaszokkal. Az utóbbi szakaszban az űrhajó legénysége súlytalansági állapotban utazik. Ennek időtartamát azonban korlátozni kell, mert hosszabb idő után a csontok és az izmok leépülése már komoly problémát idéz elő.

Váltakozó gyorsulási szakaszok az űrutazásban

Nézzünk meg egy olyan esetet, amikor az idő felét teszi ki az egyenletes sebességű, tehát súlytalansági szakasz. Itt fontos tisztázni, hogy mit értünk az utazási idő alatt, mert ez jelentősen eltér, ha a földi, indulási rendszert, vagy az űrhajóban eltöltött időt vesszük alapul, amikor a sebesség erősen megközelíti a fénysebességet és jelentős az idő dilatációja. Példánkban a földi időből induljunk ki, a teljes t időt három szakaszra bontjuk, az első a gyorsuló t₁ szakasz, a második a súlytalansági t₂, a harmadik a lassulási szakasz: t₃. A t₁ és t₃ szakasz hossza megegyezik, mert nem jelentős a Proxima Centauri sebessége a Naphoz mérten, míg legyen t₂ = 2t₁.

A relativisztikus sebesség változása állandó gyorsulás mellett

A nem-relativisztikus mechanikában állandó g gyorsulás esetén a sebesség arányosan növekszik az idővel: v = g.t. Ez azt jelentené, hogy egy év után már átlépnénk a c fénysebességet, ezért csak a relativisztikus effektusok figyelembevételével kaphatunk reális eredményt. Induljunk ki a relativisztikus sebesség formulájából, amely szerint

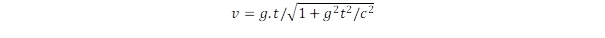
A sebességet viszonyítsuk a c fénysebességhez, ami egyszerűsíti a számítást, ha az időt c/g egységben adjuk meg. Mivel c = 3.10⁸m/s és g = 9,81 m/s², így c/g = 3,058.10⁷ s = 0,968 év. Meglepő véletlen, hogy ez az időegység milyen közel van a Föld keringési idejéhez, az évhez, az eltérés csupán 3,3%. Az idő egységének ez a választása annak felel meg, hogy az idő helyett áttérünk az x = g.t/c változóra, amikor is a sebességi formula:

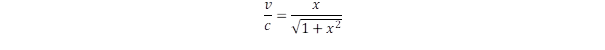
Hosszú idő esetén, azaz ha x >> 1, akkor a v sebesség a c határértékhez tart, amit nem léphet át, megfelelően a relativitáselmélet alapvetésének.

A megtett út relativisztikus számítása

A nem-relativisztikus mechanikában az állandó gyorsulás mellett megtett út s = 1/2g.t², vagy ezt átrendezve t² = 2s/g. Ha a relativisztikus sebességi formulát alkalmazzuk, akkor fellép egy új tag a kifejezésben, azaz t² = 2s/g + s²/c². Az új tag az s = c.t fény által megtett útnak felel meg. Fejezzük ki az s utat az idő függvényében, ami a másodfokú egyenlet megoldásával adható meg és térjünk át az idő esetén a c/g, míg az út esetén a c²/g egységre, azaz az út helyett az y = s.g/c² változót vezetjük be. Az így definiált egységnyi út közel azonos a fényévvel, annál csak 3,3%-kal kisebb. Ebben az egységrendszerben az állandó gyorsulás által megtett út:

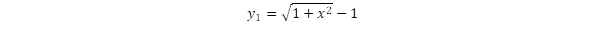
A teljes utat, amit a földi koordinátarendszerben határozunk meg, három részre bontjuk, y₁ a gyorsuló, y₂ az egyenletes és y₃ a lassuló szakasz hossza. A lassuló szakasz y₃ hossza megegyezik y₁-el, míg y₂ értékét a relativisztikus sebességformulából adjuk meg (Itt ne feledjük, hogy y₂ is a földi rendszerben érvényes távolság!):

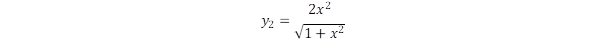
Itt a kettes faktor azért lép fel, mert t₂ =2t₁.

Az utazási idő kiszámítása

Mennyi lesz azaz idő, ami alatt az űrhajó megérkezik céljához, ha a fenti az időmegosztást választjuk? A Proxima Centauri távolsága 4,24 fényév, ami a c²/g egységekben 4,38-nak felel meg. A következő ábra mutatja az út/idő diagramot:

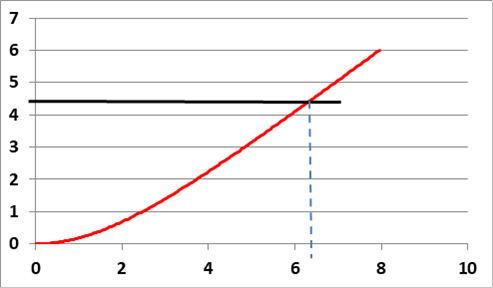
1. ábra. Az űrhajó által megtett út c²/g egységekben, ahol az idő c/g egységben van megadva, a metszéspont mutatja az érkezés idejét.

Az utazás teljes ideje földi években számolva 6,08 lesz, tehát kissé több mint hat év. Az űrhajósok azonban ennél kevesebb időt mérnek óráikon. Az idő dilatációt külön-külön figyelembe véve a három szakaszon, azt kapjuk, hogy a gyorsuló és a lassuló szakaszok ideje 1,52 évről 1,19-ra csökken, míg az egyenletes szakaszon az idő rövidülése 3,04-ről 1,64 lesz és a teljes út 6,08-ról 4,02 évre csökken, tehát rövidebb lesz, mint azaz idő, ami alatt a fény a csillagról a Földre érkezik. Ennek oka, hogy itt különböző rendszerekben mért időket hasonlítunk össze.

Az űrhajó sebességének változása az utazás során

Nézzük meg, hogyan változik az űrhajó sebessége az utazás során:

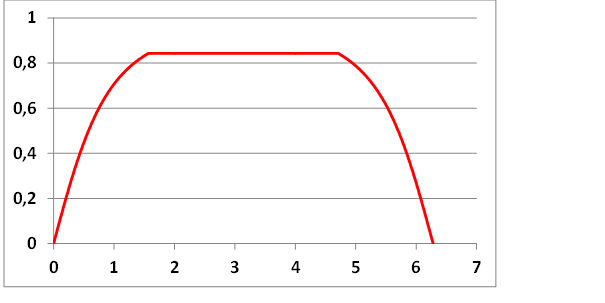
2. ábra. Az űrhajó sebességének változása a fénysebességhez viszonyítva. Az idő c/g egységben szerepel.

Megváltozott csillagképek az űrhajóban

Az ábrából látható, hogy az űrhajó sebessége jelentősen megközelíti a fénysebességet, ami jelentős mértékű relativisztikus effektushoz vezet. Nézzünk ki az űrhajó ablakából, amikor az egyenletes szakaszban vagyunk és egy megváltozott csillagképet fogunk látni. A változás nem onnan származik, hogy megteszünk egy-két fényévnyi utat, hiszen ez a távolság nagyon kicsi a Tejút 100 000 fényévnyi méretéhez képest, az eltérő csillagkép a nagy sebesség miatt van.. Csillagászaink meghatározhatják, hogy mennyire távolodtunk el Napunktól és milyen messze van még a Proxima Centauri. Ebből megállapítják, hogy a Nap-Kentauri távolság nem 4,24 fényév, hanem csupán 2,28. Jelentősen megváltozik a Nap színe is, az otthon megszokott sárga szín helyett a vörös felé tolódik el, ugyanakkor a Proxima Centauri már nem vörös, hanem a szín elcsúszik a kék felé. Ezek a változások a fény relativisztikus Doppler effektusának felelnek meg. Ha viszont nem előre, vagy hátra nézünk, hanem oldalt, akkor ugyanolyan csillagkép tárul fel előttünk, amit a Földön már megszoktunk.

A megtett út a Földről és az űrhajóból nézve

Hasonlítsuk össze az út három szakaszában a megtett utat, egyrészt a földi rendszerben, másrészt az űrhajóból nézve:

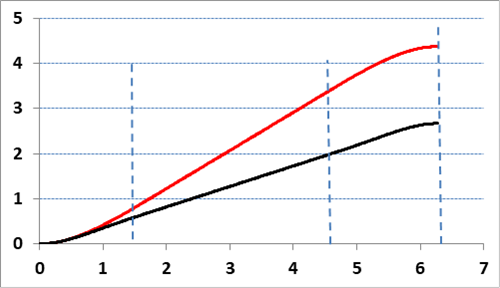
3. ábra. Az űrhajó által megtett út a földi rendszerhez képest (piros) és az űrhajóból nézve (fekete), az idő c/g, az út c²/g egységekben van megadva, a függőleges szaggatott vonalak mutatják a szakaszhatárokat

Az űrhajóban mért út a Lorentz kontrakció miatt rövidül meg, az első és harmadik szakaszban ez a 0,833 fényévet 0,604-re, a másodikban 2,564-et 1,377-re, a teljes 4,24 utat 2,68 fényévre csökkenti le.

Mennyi üzemanyag kell a csillagközi úthoz?

Annak az üzemanyagnak a mennyiségét becsüljük meg, ami a gyorsítási munkához kell. Jelöljük M₀-al a kilövéskor az üzemanyag mennyiségét és m legyen az űrhajó hasznos tömege. A gyorsítási és lassítási szakaszban az M +m tömeget kell g-vel gyorsítani, ahol a kezdeti M₀-ról csökken le az üzemanyag tömege nullára. Példánkban a megtett utat a gyorsítási és lassítási szakaszok teljes hosszában kell biztosítani. Ennek hossza a Lorentz kontrakcióval csökken, mert az űrhajó rendszerében kell figyelembe venni a távolságot, tehát az út 1,2 04 fényév lesz, ami a c²/g egységben 1,244.  A gyorsítási munka azonban fokozatosan csökken, ahogy fogy az üzemanyag. Végezzünk egy közelítő számítást arra az esetre, amikor az üzemanyag mennyisége jóval több, mint az űrhajó hasznos tömege. Ekkor az üzemanyag hosszegységre jutó fogyása arányos lesz magával az üzemanyag mennyiségével: dM/ds = -k.M. Ekkor az üzemanyag mennyisége az út során exponenciálisan csökken: M = M₀.e^-k.s. A tényleges fogyás ennél gyorsabb, mert valójában az M + m teljes tömeget kell gyorsítani, ezért becslésünknél még nagyobb mennyiségű üzemanyagra lesz szükség. A lassítási szakasz végén az űrhajó nem tartalmaz üzemanyagot és így a teljes tömeg lecsökken m-re. Tehát megérkezéskor m = M₀.e^-k.s . azaz

M₀/m = e^k.s

Az összefüggés mutatja, hogy a megtett út hosszától exponenciálisan függ a szükséges hajtóanyag mennyisége.

 Az M tömegű üzemanyagból nyerhető maximális energia a nyugalmi energiával egyezik meg, ami M.c², ennél csak kisebb lehet a ténylegesen kinyert energia, aminek hatásfokát jellemezzük η-val: ηMc².  Az egységnyi úthossz alatt nyert kηMc²energia hozza létre az M.g gyorsítási munkát, ezért

k = g/ηc². Ily módon alsó becslést kapunk az üzemanyag arányára a hasznos tömeghez képest:

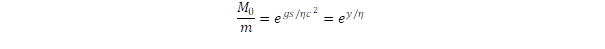
Az üzemanyag hatékonyság szerepe az űrutazásban

Ha bármilyen kémiai üzemanyagot használunk a hatásfok kisebb mint egymilliárd, nukleáris bomláskor felszabaduló energiát használva sem érhetünk el egy tízezrednél nagyobb hatásfokot, még fúziós reakciókat felhasználva sem remélhetünk többet 1 százaléknál. Esetünkben y = 1,244 ezért még fúziós reaktor esetén is beláthatatlanul nagy mennyiségű üzemanyagra lenne szükség.

A leghatékonyabb energiatermelés antirészecske reaktorral

Tehát az expedíció alapkövetelménye, hogy az egységhez közel legyen az energiafelhasználás hatásfoka. Lehetséges-ez? Elvben igen, ha az anyag-antianyag annihiláció lenne az energiaforrás, mindenekelőtt az antiproton és a protonok annihilációja lehetne az alap. A probléma természetesen az antiprotonok összegyűjtése és tárolása lenne, mert olyan tartályra lenne szükség, ahol az antirészecske nem érintkezhetne a tartály anyagával. Az antiproton töltött részecske, ezért mágneses térben körpályára kényszeríthető, emellett ha negatív töltésű lenne a tartály, akkor ez eltaszíthatná magától az antiprotonokat. Tehát elvben létrehozható ilyen elektromágneses csapda, de persze ehhez is energia kell, ami a működést biztosítja.

Az antirészecske reaktor kockázatai

Az antiprotonokat a kozmikus sugárzásból lehetne nyerni, mert annak energiája elég, hogy létrejöjjenek ezek a részecskék, de ha ezek a részecskék nagy tömegben vannak összegyűjtve, akkor a kockázat óriásira nő. Akkora mennyiség kellene, ami sokszorosan meghaladja a földön jelenleg tárolt hidrogénbombák nukleáris töltetének teljes tömegét és egy esetleges robbanás hatásfoka ennek több mint százszorosa lenne. Elég egy apró technikai hiba, és ha létrejön a robbanás az nem csak a földi életet pusztítaná el, hanem szétrobbantaná a föld kérgét is. Még nagyobb veszély fenyegetné az űrhajósokat, mert a fénysebesség közelében már nem lehetne előrelátni, ha valamilyen nagyobb űrobjektum kerülne a pálya közelébe, és a manőverezés is nehéz ekkora sebességnél. Így aligha lehetne olyan biztonsági rendszert kifejleszteni, amely elegendő mértékben csökkentené az ütközés és emiatt a robbanás kockázatát.

Drónok küldése a Proxima b Centaurihoz

Az elmondottak miatt bármilyen magas szintre emelkedjen a technika, a csillagközi expedíciónak rendkívül nagy lenne a kockázata. Járható út lehet azonban az automatikus űreszközök, drónok küldése, amelyeket földről irányított energiaforrások (lézerek) segítségével fel lehet annyira gyorsítani, hogy reális idő alatt elérjék a szomszédos csillagokat és onnan küldjenek számunkra híradást a Proxima b Centauri világáról. A második Földnek elnevezett bolygóra történő utazásra ezért nem látok reális esélyt, ez megmarad mindörökre a fikciók világában.

A korábbi bejegyzések összefoglalását és a megfelelő linkeket lásd: „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”.