Bevezetés

Elöljáróban felhívom a figyelmet Patkós András kitűnő írására, amit „A neutrínó befejezetlen története” címmel tett fel az internetre (www.termeszetvilaga.hu/fizika_eve/fizika/patkosa.html). Ebben a bejegyzésben egy olyan elképzelést mutatok be, amely a neutrínó történetét segít továbbvinni, annak tudatában, hogy a nyitott kérdések megválaszolása még további kutatásokat tesz szükségessé.

A Standard Modell képe a neutrínóról

 Az elemi részecskék tulajdonságait a modern fizika a Standard Modellben foglalja össze. Ebben a modellben a neutrínókat nulla nyugalmi tömegű részecskéknek tekintik. Ennek oka, hogy a különböző mérések szerint a neutrínó sebessége – a mérési hibahatáron belül – egyezik a fénysebességgel. A speciális relativitáselmélet szabályai szerint csak nullatömegű részecske érheti el a fénysebességet, mert ezen a sebességen bármilyen kicsi is legyen a nyugalmi tömeg a mozgási tömeg végtelenné válna. Ez a relativisztikus kovariancia törvény egyik következménye.

A neutrínó felfedezése

A különböző részecskefizikai megfigyelések arra vezettek, hogy nem csak egyféle neutrínó létezhet, hanem meg kell különböztetni a neutrínók három típusát. Az első típus az elektron-neutrínó, amit azért neveznek így, mert az elektron (illetve annak anti-részecskéje a pozitron) magátalakulások során való képződésekor jelenik meg.. A neutron béta-bomlásakor két részecske figyelhető meg, egy proton és egy elektron. A töltésmegmaradás elvével nincs is baj, de sem az energia sem az impulzus mérleg nem stimmel, valami mindig hiányzik. Úgyszintén baj van az impulzusnyomaték megmaradásával is: az ½ spinű neutron bomlásakor csak úgy képződhet két ½ spinű fermion, ha van egy harmadik ½ spinű részecske is. Emiatt kellett feltételezni egy gyengén kölcsönható új részecskét, amit a semleges töltésű, S = ½ spinű neutrínónak neveztek el. A neutrínó kísérleti kimutatása komoly nehézségekbe ütközik, mert nem vesz részt sem az elektromágneses, sem az erős nukleáris kölcsönhatásban, de kimutatása még sem lehetetlen. A gyenge kölcsönhatás mechanizmusában ugyanis, ha a neutrínó protonokkal ütközik, akkor képes megfordítani a béta-bomlás folyamatát, amikor is a protonok neutronokká való átalakulását pozitronok képződése kíséri. A proton-neutron átalakulások, illetve a pozitronok  kimutatása azonban azt igényli, hogy ezek a folyamatok kizárólag a neutrínó ütközések és ne a kozmikus, vagy gamma-sugárzás által jöjjenek létre és emiatt a méréseket minden egyéb sugárzástól mentes környezetben (mélyen a föld alatt lévő barlangokban) kell végrehajtani.

A neutrínók típusai

Ilyen típusú berendezést ma már a Föld különböző helyein létesítettek, ami lehetőséget biztosít az ellenőrzött körülmények között képződő neutrínók megfigyelésére. A már említett elektron típusú neutrínók mellett beszélhetünk müon és tau típusú neutrínókról is. A müon és tau részecskék az elektronnal azonos elektromágneses tulajdonsággal, de nagyságrendekkel nagyobb tömeggel rendelkeznek, amelyek azonban rövid élettartalmúak és elektronra való bomlásuk során két, illetve három neutrínót bocsátanak ki. A bomlásuk során a tömegveszteségből arra lehet következtetni, hogy nagyobb energiát visznek magukkal, mint a neutron bomláskor képződő neutrínók. Ezért feltételezhető, hogy ezek a neutrínók eltérő tömeggel is rendelkeznek.  Ez azonban csak feltételezés, mert a tömegük mérésére nincs közvetlen lehetőség. Indirekt módon azonban becslés adható tömegük felső határára. Egy ilyen lehetőség, ha ismerjük E energiájukat és a v utazási sebességet, mert a relativisztikus tömegnövekedés szabálya szerint:

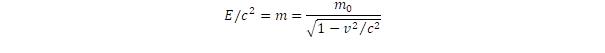
Neutrínó oszcilláció: van-e nyugalmi tömege a neutrínóknak?

Az eddig elvégzett mérések szerint azonban a neutrínók sebessége a hibahatáron belül egyezik a fénysebességgel, ami vagy azt jelenti, hogy a nyugalmi tömeg nulla, vagy csak nagyon kis tömeggel rendelkeznek (például az elektron tömegének legalább 40 ezerszer kisebbel). Itt a becslés alapja a mérési hiba nagyságából számolható.

Hasonló becslés adható, a neutrínó oszcilláció alapján is. Itt arról van szó, hogy a három különböző neutrínó spontán módon átalakulhat egymásba és az oszcillációs hossz a tömegek négyzetének különbségéből számolható. Az oszcilláció létrejötte, ezért a jelenlegi elmélet szerint azt is jelenti, hogy létezik nullától különböző tömegű neutrínó is. Földi körülmények között azonban ilyen oszcilláció nem volt megfigyelhető, feltételezhetően a földi körülmények között elérhető távolságok rövidsége miatt. Ez alapján adtak becslést a háromféle neutrínó lehetséges tömegének maximális mértékére.

 A kozmikus sugárzásból, illetve a Napból származó neutrínó fluxus méréséből azonban egyértelművé vált, hogy a neutrínó oszcilláció jelensége tényleg létezik. A Nap fúziós folyamataiból nagy megbízhatósággal becsülhető a Földre érkező neutrínók fluxusa, viszont a ténylegesen mért fluxus ennek csak a fele. Ezt a Nap-neutrínó deficitet értelmezik a neutrínó-oszcillációval, mert a mérés csak egy megadott energiájú neutrínót tud észlelni és a feltételezés szerint az oszcilláció során átalakuló neutrínók energiája már kívül esik a detektorok érzékelési tartományán. A neutrínó oszcillációjára azonban nem csak a Napból érkező részecskék számlálása, hanem a szupernóva robbanásból származó neutrínók észlelése is utal. Szintén a neutrínó-oszcilláció elméletét támasztja alá az atmoszférikus neutrínók detektálása is, amikor a kozmikus sugárzás hatására képződő müonok mennyiségét vetik össze a bomlásból származó neutrínók fluxusával.

A kísérleti adatok alapján nagy megbízhatósággal állíthatjuk, hogy a neutrínó-oszcilláció jelensége tényleg létezik, de jeleni-e ez, hogy valóban rendelkeznek a neutrínók nyugalmi tömeggel? Véleményem szerint nem és ezt fogom a következő érvekkel alátámasztani.

A relativisztikus kovariancia elv fontossága a részecske fizikában

Gondolatmenetem kiindulópontja a speciális relativitáselmélet kovariancia elve. Ennek két része van, az egyik a mechanikai, amelyik az energia, impulzus és a nyugalmi tömeg kapcsolatát adja meg, a másik az elektrodinamika alapegyenleteiből származtatható, amelyik a skalár és a vektorpotenciál  segítségével egészíti ki az energia kovariáns alakját:

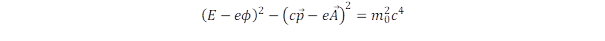
Ez az összefüggés alapvető jelentőségű az elemi részecskék meghatározása szempontjából, mert a kovariancia a téridő alapvető tulajdonságát tükrözi és emiatt VALAMENNYI részecskére vonatkozik.

A Dirac egyenlet születése

Dirac volt, aki megmutatta, hogyan származtatható ebből a relativisztikus elektron tulajdonságait meghatározó kvantummechanikai egyenlet, amikor is a négyzetgyökvonást négydimenziós spinorok segítségével hajtotta végre. Lásd erről részletesebben „A Dirac-egyenlettől az általános fermion egyenletig” című bejegyzést, itt csak az alapvető formulákat mutatom be.

Itt α és β jelöli az antikommutáló spinorokat és I₄  a négydimenziós egységmátrix.

 Az eljárás valójában négy csatolt differenciálegyenlettel határozza meg az elektron energiáját elektromágneses mezőben. Ez a négydimenziós függvénytér felbontható két kétdimenziós függvénytérre a mátrixok direktszorzatát bevezetve (Lásd a fenti bejegyzést).

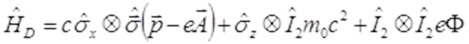
Itt a direktszorzatokban a kétdimenziós Pauli mátrixok: 

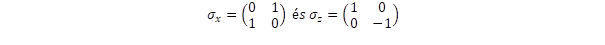
 szerepelnek, amelyek egymással antikommutálnak:

 sorrendjük a direkt szorzatban meghatározott, ezenkívül feltüntettem az I₂ kétdimenziós egységmátrixot is.

Kétdimenziós alterek: az előjeltér és a spin

Az első kétdimenziós tér a pozitív és negatív energiájú megoldásoknak felel meg, amit a nyugalmi energiát szorzó  σ_z mátrix jelöl a +1 és -1 diagonális elemek által. Mivel a kovariáns kifejezésben az energiatagok négyzete szerepel, ezért a négyzetgyökvonás kétértékűsége miatt fellépnek negatív energiájú megoldások is. Az impulzustag viszont a nem-diagonális σ_x mátrixszal szorzódik az első helyen, amely nem kommutál a nyugalmi energia σ_z mátrixával. Voltaképp ez felel meg a relativisztikus tömegnövekedésnek az alkalmazott formalizmus keretein belül.  Dirac a végtelen nagyságú negatív energiájú megoldás fellépése miatt tételezte fel, hogy valamennyi negatív energiájú állapot eleve betöltött. Erre a feltevésre azonban nincs szükség, mert az energiaoperátor definíció szerint az időszerinti differenciálhányados: E = hi/2π d/dt és így a negatív energiájú állapot voltaképp az idő irányának megfordítását jelenti. Viszont világunkban az idő iránya nem fordítható meg (nem mehetünk vissza a múltba), ezért a kovariancia kifejezést ki kell egészíteni avval a szabállyal, amely megtiltja a negatív energiájú állapotba való átmeneteket.

A második kétdimenziós tér definiálja a spint, azaz az elektron saját impulzusnyomatékát, aminek két lehetséges vetülete van. A spin eredete tehát szintén a kovariancia elvre vezethető vissza. A Standard Modell szerint valamennyi elemi részecske rendelkezik spinnel, ebben mutatkozik meg, hogy a kovariancia elv érvényes nem csak az elektron és pozitron, hanem minden egye részecske számára.

Felbontás nyolcdimenziós spinorokkal: az általános fermion egyenlet

Fölmerül a kérdés, hogyan tudjuk a többi elemi részecske alapegyenletét is visszavezetni a kovariancia elvre. A négyzetgyökvonás Dirac által elvégzett felbontása négydimenziós spinorokkal a legegyszerűbb, de nem az egyetlen lehetséges megoldás. Ahogy azt a korábban jelzett bejegyzésben kimutattam, hasonló felbontás elvégezhető nyolcdimenziós spinorokkal is, ahol a spinorok megtartják az antikommutatív felcserélési szabályokat.

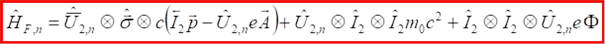
 Ez esetben egy újabb kétdimenziós függvényteret kapunk, amit a kétdimenziós U_2,n uniter mátrix és az avval antikommutáló párja jelöl. Ezek a mátrixok a diagonális σ_z és a nulla diagonális elemű σ_x mátrixokból épülnek fel:

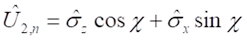
illetve

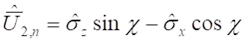
Az n kvantumszám határozza meg a χ szöget, amelynek értéke 3, 2, 1 és 0 lehet és definiálja az elektron-pozitron párt, az up-antiup, a down-antidown kvarkokat, valamint a neutrínót:

A töltés, tömeg és impulzus operátor a spinor térben

Az U_2,n mátrix a direkt szorzat harmadik pozíciójában írja le az új kétdimenziós teret, ami a Standard Modellben a részecske-antirészecske kettősségnek felel meg, és amit az általam javasolt kettősforgásos modellben a két királis szimmetria ad meg. A részecske, illetve antirészecske töltését a töltésoperátor két királis állapotban képzett várható értéke határozza meg:

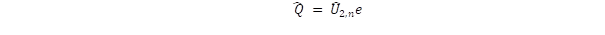
Ebben a reprezentációban a töltés többé nem egyszerű konstans, hanem a kétdimenziós Pauli-mátrixokkal kifejezett operátor. Az általános fermion egyenlet abban is eltér a Dirac egyenlettől, hogy a direkt szorzat első pozíciójában σ_z helyett U_2,n, illetve σ_x helyett annak antikommutáló párja szerepel. Ez a nyugalmi tömeg és az impulzus operátor definícióját jelenti a spinorok „előjel” terében:

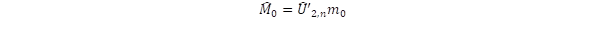
illetve:

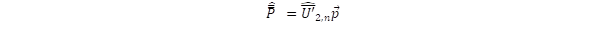
Itt a vesszőzéssel azt hangsúlyozom, hogy ezek az operátorok az energia kétdimenziós “előjel” terében hatnak.

Az elektron-pozitron pár a fermion egyenletben

 Az n = 3 esetben az U_2,n mátrix a diagonális σ_z Paul mátrixszal egyezik meg, míg annak antikommutáló párja a nem-diagonális σ_x lesz, ami azt jelenti, hogy az elektron és a pozitron TÖLTÉS és TÖMEG ÁLLAPOTÚ részecske  –e illetve +e töltéssel és a két részecske nyugalmi tömege egyaránt lehet +m₀ és –m₀. Ebben a felfogásban a pozitron  nem a teljesen betöltött negatív energiájú „tengerből” hiányzó „lyuk”, hanem az elektron királis tükörképe: az egyik kiralitás felel meg az elektronnak, a másik a pozitronnak. Hasonlóan a tömeg sem konstans többé, hanem operátor. Ebben a formalizmusban már valamennyi mennyiség operátor lesz. A Standard Modell fermionjait a részecske kvantumszám jellemzi, amelynek értéke 3, 2, 1 és 0 lehet és leírják az elektron-pozitron párt, az up-antiup, a down-antidown kvarkokat, valamint a neutrínót.

A neutrínó mint impulzus részecske

A kvarkokkal majd a következő bejegyzésben foglalkozunk, itt most célunk a neutrínó tulajdonságainak megértése, amely az n = 0 részecske kvantumszámhoz tartozik. Ekkor σ_z és σ_x szerepet cserél, a töltés és tömeg operátor nem-diagonális alakot ölt, szemben a diagonális impulzus operátorral. Ez azt jelenti, hogy a neutrínó IMPULZUS ÁLLAPOTÚ részecske! A töltés és a tömeg várható értéke egyaránt nulla, mert σ_x   nem rendelkezik diagonális elemekkel sem a részecske és sem az antirészecske állapotban, ezért a neutrínót önmaga antirészecskéjének kell tekinteni. Az impulzus állapot viszont azt jelenti, hogy a neutrínó három típusa különböző SAJÁT IMPULZUSSAL rendelkezik, tehát annak ellenére megkülönböztethetők, hogy nyugalmi tömegük egyaránt nulla. Ez a tulajdonság a fotonokéval egyezik, amelyek szintén nulla tömegűek, de rendelkeznek impulzussal, amit a hullámszám határoz meg. A neutrínó nulla nyugalmi tömege megengedi, sőt megköveteli a fénysebességű haladást és az impulzusból számolható hullámhosszak különbsége határozza meg az oszcillációs tulajdonságokat. Tehát ha jellemezni akarjuk a neutrínókat, akkor nem a tömegéről kell beszélni, hanem arra kell törekedni, hogy megismerjük  a három alaptípus impulzusát.

A részecske fizika megoldatlan kérdései

A bevezetőben feltett kérdésre tehát az a válaszom, hogy a neutrínó impulzus állapotú részecske, amely lehetővé teszi a háromféle neutrínó spontán egymásba alakulását. A részecske fizika legfontosabb nyitott kérdésének azt tartom, hogy szemben a fotonokkal, amelyek tetszőleges energiával, frekvenciával és impulzussal rendelkeznek, miért van a fermionoknak jól definiált tömege, azaz sajátfrekvenciája. Azt tartom valószínűnek, hogy ez a kettős forgással függ össze, amely rezonanciaszerűen jöhet létre. De mi kényszeríti ki a rezonanciát, milyen erők játszanak szerepet ebben? Talán ha erre a kérdésre ismernénk a választ, akkor arra is válaszolni tudnánk, hogy miért éppen 207-szer nehezebb a müon az elektronnál, vagy a tau részecske miért 3477-szer nagyobb tömegű, mint az elektron. Ilyen és az ehhez hasonló kérdésekre a válasz még várat magára, ezért még messze vagyunk attól, hogy a részecske fizika alapkérdéseit tisztába tegyük.

A fizika kalandja blog további bejegyzéseinek összefoglalóját a megfelelő linkekkel együtt: lásd „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”