Rockenbauer Antal

Megfordítható-e az idő iránya?

A történelem kerekeit nem lehet visszaforgatni. Megszületünk, felnövünk, megöregszünk, meghalunk, közismert tények, közismert igazságok. De mindennapi életünkben is tapasztaljuk, hogy az események nem megfordíthatók. Felvehetjük filmre, videóra, ahogy az alma lehullik a fáról, vagy ha egy pohár leesik az asztalról és darabokra törik, és nagyon mulatságos, ha visszafelé játsszuk a filmet és látjuk, ahogy az almák felreppennek a földről és visszakapaszkodnak a fára, vagy, ahogy a pohár széttört darabkái összeszaladnak, újra összeforr a pohár majd fellendül az asztalra. Nevetünk rajta, hiszen olyan nyilvánvaló, hogy amit látunk az lehetetlen. De bármennyire is nyilvánvaló, hogy az események sorrendje nem fordítható meg - a tudomány számára egyáltalán nem könnyű megtalálni az események megfordíthatatlanságának, irreverzibilitásának okát. A továbbiakban néhány gondolatot fogalmazok meg a kérdés tisztázására, felvetve azt a kérdést, hogy milyen szerepet játszanak bizonyos fizikai fogalmak az idő irányának meghatározásában, hogy merre felé is mutat az idő nyila. Ennek során kitérek az entrópia és az evolúció kapcsolatára és mindkét fogalmat a szokásosnál általánosabb keretek között értelmezem. Az evolúció fogalmát az életformák kibontakozása mellett kiterjesztem az univerzum fejlődésére is, az entrópiáról szólva felvetem a kérdést, hogy mennyiben játszhat szerepet az elemi részecskék és atomok spontán folyamataiban.

Energia: állandóság a változásban

            Kiindulópontunk az energia fogalma. Minden fizikai mozgás legfontosabb jellemzője, amiből származtathatjuk, matematikailag levezethetjük a testek mozgást kezdve az elem részecskéktől egészen a csillagokig, galaxisokig. Minden mozgásban, minden átalakulásban az energia megmarad. Ez a fizikai egyik legfontosabb alaptétele. Bár pontosabb megfordítani a kérdést: mi az, ami minden mozgásban, minden változásban és átalakulásban állandó: valójában ez a fizikai mennyiség az energia. A mozgások leírásában – függetlenül a leírás szintjétől, akár a newtoni mechanikát, vagy az elemi részecskék mozgását leíró kvantummechanikát alkalmazzuk-e beleértve a relativisztikus effektusokat és a térelméleteket is – az energiát két részre bonthatjuk: a sebességtől függő mozgási, azaz kinetikus energiára és a testet mozgató vonzó és taszító erők hatását leíró potenciális energiára. Ennek a két energiaformának a viszonya, egymásba alakulása jellemzi a mozgást. Nézzük a fáról leeső alma példáját. Amíg az alma fent van a fán, addig a gravitációs potenciál értéke nagyobb. Eséskor ez a potenciális energia alakul át fokozatosan mozgási energiává és ez idézi elő az alma gyorsuló mozgását. De miért nem pattan fel az alma a földre való leérkezést követően? Ennek megértéséhez vegyük az idealizált pingpong labda példáját, amit ha leejtünk az asztalra először a gravitációs potenciál alakul át mozgási energiává. Az asztalra érve a labda belapul, amelynek mértékét a leesési sebesség határozza meg. A lapultság fokát a rugalmas potenciállal jellemezetjük, amelyik akkora értékre nő meg, amekkora a leeséskor érvényes kinetikus energia volt. Ezt úgy értelmezzük a fizikában, hogy a mozgási energia révén munkát végeztünk a rugalmassági erővel szemben. Másképp fogalmazva a munka a mozgási energia átalakítása révén nyert potenciális energianövekedés. A rugalmas potenciális energia visszaalakul mozgási energiává, amikor a labda visszanyeri eredeti alakját és a labda felpattan. Ennek során a mozgási energia ismét potenciális energiává alakul, és ha nincs veszteség, akkor ugyanolyan magasra ugrik fel a labda, mint amikor elengedtük. A labda miután elérte a maximális magasságát újra lefelé fog esni és a ciklus folytatódik. Ideális labda azonban nincs, az átalakulások során mindig fellép valamekkora veszteség, ezért a visszapattanás mértéke fokozatosan csökken és a labda végül megáll. A leeső labda és az alma között az a különbség, hogy az alma leesése után elvész a teljes mozgási energia, míg a labda esetén a veszteség csak részleges. Ez az átalakulási vesztesége okozza, hogy nincs örökmozgó gépezet sem. Akármilyen ötletesen építünk fel egy gépet, amelyben a mozgási energia és a potenciális energia különböző formái alakulnak át egymásba, a veszteség előbb utóbb megállítja a működést, ha nem pótoljuk vissza az energiát valamilyen külső forrásból.

Hőenergia: rendezetlen mozgások

            De mi lesz az elveszett energiával, hiszen az energiamegmaradás tétele szerint energia nem tűnhet el. Ez az a pont, amikor eljutunk a hőenergia fogalmához és az entrópiához. Az első veszteségforrás a levegő közegellenállása. A labda ütközik a levegő molekuláival, aminek révén az ütköző molekulák mozgási energia megváltozik. Ez átlagban megnöveli a levegő molekulák rendezetlen, un. termikus mozgásának energiáját, ugyanakkor a labda molekulái is termikus mozgásokat, például rezgéseket végeznek, amelyek intenzitása az ütközés miatt megnövekszik. Ezt a növekedést nevezzük a belső energia, vagy hőenergia változásnak. A hőenergiát is számba véve teljesedik ki az energiamegmaradás törvénye, amit a termodinamika mint az első főtételt tart számon. A hőenergia forrása a labda kinetikus energiájának csökkenése: a közegellenállás miatt kevésbé gyorsul fel a labda, mint tenné azt vákuumban. További veszteség lép fel, amikor a labda az asztalra érkezik. Az ütközés során az asztal atomjainak és molekuláinak rezgési állapota is megváltozik és ugyanez érvényes a labda molekuláira is. Emiatt a rugalmas potenciállal szemben végzett munka kisebb lesz, mint a leesés pillanatában fennálló mozgási energia. Valójában a molekularezgésekhez is tartozik egyfajta kinetikus energia, de ennek jellege eltér a labda helyváltoztató mozgásának kinetikus energiájától. Amíg a labda mozgásakor valamennyi molekula együtt halad ugyanakkora sebességgel, addig a termikus rezgések iránya molekuláról molekulára más és más, ezért úgy mondjuk, hogy a hőenergia rendezetlen mozgás szemben a labda „rendezett” mozgásával. A rendezetlen mozgások teljes energiája tehát a hőenergia, amit kifejezhetünk az egyes rezgések, vagy véletlenszerű molekuláris mozgások átlagos energiájával. Az átlagos energia, illetve a különböző energiájú véletlenszerű molekuláris mozgások eloszlása határozza meg a test hőmérsékletét az abszolút un. Kelvin skálán. Ennek nulla pontja a Celsius skálán -273 foknak felel meg. A kvantummechanika szerint még az abszolút zérus fokon sem állnak le a rezgések, illetve molekuláris mozgások (ezt nevezik zérus-ponti rezgésnek), csupán ekkor minden rezgés, illetve mozgás a lehető legkisebb energiával rendelkezik. A jelenség magyarázatát a bizonytalansági reláció adja meg, amivel a későbbiekben még foglalkozni fogunk.

Entrópia: a változások iránya

            Most térjünk át az entrópia fogalmára. Különböző irányokból indulhatunk el. A klasszikus út a hőátadást jelensége. Ha két különböző hőmérsékletű test érintkezik, akkor a melegebb felmelegíti a hidegebbet, más szóval hőáramlás következik be a melegebb helyről a hidegebb felé. Legyen T₁ és T₂ a két hőmérséklet, ahol az előbbi rendelkezik nagyobb értékkel és az átadott hőmennyiség legyen ΔQ. Az első test lead ΔQ hőmennyiséget, a második az energiamegmaradás törvénye szerint ugyanannyit vesz fel. Entrópia változásként definiáljuk a hőmennyiség átadás és a hőmérséklet hányadosát a termikus kapcsolatban álló kétkomponensű rendszer esetén:

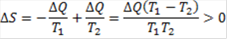
Az entrópia változás mindig pozitív, ami egyenértékű avval a kijelentéssel, hogy a hő a magasabb hőmérsékletű helyről vándorol az alacsonyabb hőmérsékletű hely felé. A hőáramlás iránya – hacsak nem használunk fel valamilyen külső energiaforrást, mint például elektromos energiát a hűtőgépekben – nem fordítható meg. Az entrópiát ezért a megfordíthatatlanság, más szóval az irreverzibilitás mértékének is tekinthetjük. Az entrópia növekedés valamennyi energiakonverzió esetén bekövetkezik, ha a test kinetikus energiáját konvertáljuk a potenciális energia valamilyen formájába, majd a folyamatot megfordítva visszanyerjük a mozgási energiát, akkor a kinetikus energia egy része mindig elvész, pontosabban hőenergiává alakul át. Ugyanez történik, amikor potenciális energiából nyerünk kinetikus energiát, majd ennek munkájával újra potenciális energiát hozunk léte: a teljes ciklus mindig hőtermeléssel jár, ennek mértékét a képzett hőmennyiség és a hőmérséklet arányával, azaz az entrópia növekedésével jellemezhetjük. Ezt a felismerést fogalmazza meg a termodinamika második főtétele: perpetuum mobile nem építhető fel, ami egyenértékű avval a megállapítással, hogy zárt rendszerben az entrópia mindig növekszik.

Entrópia a statisztikus mechanikában

Eddig tehát két fizikai fogalommal foglalkoztunk: az energiával és az entrópiával, az előbbi mennyiség, amelyik minden mozgásban és átalakulásban megmarad, a másik, amelyik mindig növekszik. Az előbbi képviseli a változásban az állandóságot, a második adja meg a változások irányát. Várható, hogy ez az utóbbi játszik döntő szerepet az evolúcióban is. Mielőtt az evolúció fogalmára térnénk át, vizsgáljuk meg az entrópia fogalmának egy másfajta értelmezését. Amit eddig elmondtunk az nem függ a vizsgált anyagok jellegétől, összetételétől, nem fontos hogy homogén, vagy inhomogén rendszerről van-e szó, csak azt kötöttük ki, hogy a rendszer zárt legyen, azaz energiacsere ne következzen be a környezettel. De felvethetjük a kérdést, hogy milyen mikroszkopikus folyamatok állnak az entrópia növekedés mögött? Evvel a kérdéssel foglalkozik a statisztikus mechanika. Bármilyen makroszkopikus rendszerben óriási számú molekula, vagy atom van. Például a víz 18 grammjában N = 600 000 000 000 000 000 000 000 = 6x10²³ a molekulák száma. Ezt nevezzük az Avogadro számnak. Hogy milyen óriási számról van szó, azt egy hasonlattal érzékeltetjük. Töltsünk meg egy gyűszűt vízzel, majd öntsük ki! Közben hajtsunk végre egy varázslatot: nőjön meg minden vízmolekula akkorára, mint egy pingponglabda. Ekkor a víz kifolyik a szobából, elönti először környezetünket, végig fut az országon, sőt egész Európán is, de itt sem áll meg, hanem átfut az óceánokon és elönti az egész Földet. De milyen magasan, csak a legmagasabb hegyek látszanának ki, mert a víz szintje 4 kilométer lenne!

Ilyen hatalmas számú molekula mozgását egyenként lehetetlenség leírni, hiszen ehhez az összes molekula mozgását ismerni kellene. Vannak azonban olyan átlagos jellemzői a rendszernek, amellyel az egész rendszer rendelkezik. A statisztikus mechanika termodinamikai törvényei legkönnyebben az ideális gázok esetére adhatók meg. Ideálisnak tekintünk egy gázt, ha a molekulák ütközése nem hoz létre változást a molekulák szerkezetében csupán mozgásuk irányát, sebességét és kinetikus energiáját változtatja meg. A vízgőz molekuláinak ütközésekor az impulzusváltozások átlaga (impulzus = tömeg szorozva a sebességgel) kapcsolódik a nyomáshoz, a kinetikus energia átlaga a hőmérséklethez, ez a két mennyiség pedig zárt rendszerekben a gáz állapotát egyértelműen jellemzi.

Entrópia: iránytű a legvalószínűbb állapotok felé

A statisztikus mechanikában az entrópia definíciójához a valószínűség fogalmán keresztül jutunk el. Ugyanakkora hőmérséklet, amit az átlagos energiával jellemezhetünk, a részecskék energiájának sokféle eloszlásával valósulhat meg. Lehet akár mindegyik molekulának azonos energiája, sőt mozgások iránya is megegyezhet. Valójában ez az eset valósul meg a mozgásban lévő szilárd testek esetén, mert ekkor a molekulák közötti összetartó erő egyben tartja a testet. De képzeljük el, hogy valamilyen okból a test széthasad molekuláira. Ekkor a molekulák egymástól független mozgásokat végeznek, ami ütközésekkel jár és a végeredmény valamilyen kaotikus mozgás lesz. Ezt a rendszert már gáznak nevezzük, ahol a molekulák a legkülönbözőbb energiával rendelkeznek. A kérdés az, hogy milyen az energia eloszlás? Van olyan eloszlás, ami csak egyféleképp valósulhat meg, ez volt a kiinduló példa az együtt haladó molekulák esetében, de lehet olyan eset is, amikor egyetlen molekula veszi át a gáz teljes energiáját. Ilyen esetből már jóval több van, mert bármelyik molekula szóba jöhet. Természetesen ez az eloszlás is rendkívül valószínűtlen. Viszont sokkal többféle módon valósulhatnak meg az olyan eloszlások, ahol a részecskék energiája különböző értékeket vehet fel. Az egyes eloszlásokat nevezzük mikroállapotnak, amelyek közül az valósul meg, amelyik a lehető legnagyobb számú kombinációban jöhet létre. A mikroállapotok számához kapcsolódik az entrópia fogalma, ami arányos ennek a számnak a logaritmusával. Az arányossági tényező az R általános gázállandó. Ugyanez a gázállandó szerepel az ideális gáz nyomása (p), térfogata (V) és a hőmérséklet (T) közötti összefüggésben: p.V = R.T. Azokban az állapotokban, amelyek kisebb számban valósulhatnak meg, és így kisebb az entrópiájuk, mindig van bizonyos fokú rendezettség, ezért az entrópia növekedésre vezető folyamatok a rendezetlenség fokát növelik meg. Szokásos még az entrópiát az információval is összekapcsolni. A rendezett mozgást jóval kevesebb információ segítségével ismerhetjük meg, ha viszont nagyon nagy a lehetséges állapotok száma, akkor nagyon sok információt kell összegyűjtenünk, ha a nagyszámú molekula mozgásának teljes leírására törekszünk. Ebben az értelmezésben az entrópia a rendszer állapotának meghatározásához szükséges információ alapján definiálható.

Lokális entrópia csökkenése kötött állapotokban

De szükségünk van még egy további lépésre, hogy eljussunk az evolúció fogalmához. Az entrópia úgy nevezett extenzív mennyiség, ami a teljes rendszer összefoglaló paramétere. A mikroállapotok száma azonban visszavezethető lokális tulajdonságokra. Ha valamilyen V térfogatban N számú részecske, atom vagy molekula van, akkor meghatározhatjuk a komponensek átlagos távolságát. De mekkora annak a valószínűsége, hogy két részecske éppen r távolságban van egymástól, ha ez a távolság kisebb az átlagos távolságnál? Ennek valószínűsége arányos az r sugarú gömb felületével, azaz r²-tel. A részecskék térbeli eloszlásához rendelhetünk egy lokális entrópiát, amelyik log(r²)=2log(r) kifejezéssel arányos. Minél kisebb ez a távolság, annál kevésbé valószínű, hogy a véletlenszerű eloszlásban két részecske éppen ekkora távolságban legyen egymástól. A részecskék között azonban különböző típusú vonzóerő léphet fel, ami kötött állapotot hozhat létre, ha a távolság kicsi. Például protonokban, neutronokban és más elemi részecskékben két, vagy három kvark között gluonok közvetítik a vonzást, protonokat és neutronokat a magerők egyesítik atommagokká, az atomok a pozitív töltésű atommagból és elektronokból állnak, ahol az elektromos töltések közötti Coulomb kölcsönhatás játszik szerepet, de az atomok is egyesülhetnek molekulákká az elektronok által létrehozott kémiai kötések által, a molekulák között is létrejön vonzó kölcsönhatás szilárd testeket létrehozva, a nagy tömegű csillagokat, bolygókat és más égi objektumokat pedig a gravitáció tartja össze. A vonzó kölcsönhatások közös vonása, hogy annál erősebbek, minél kisebb a távolság az objektumok között. Van azonban egy kvantumfizikai törvény, amely megakadályozza a teljes összeolvadást, nevezetesen a bizonytalansági reláció. Ennek egyik megnyilvánulása a pozíció és az impulzus közötti kapcsolat: minél közelebb kerül egymáshoz két objektum, annál bizonytalanabbá válik az impulzus. A bizonytalanság mértékét fejezi ki a h Planck állandó, amelyik a kvantumos tulajdonságok alapköve. A kinetikus energia négyzetesen függ az impulzustól, amíg elhanyagolhatjuk a relativisztikus hatást, ha viszont a relativisztikus effektusok fontosak bonyolultabb az összefüggés a kinetikus energia és az impulzus között, de ekkor is az impulzusnál gyorsabban nő a kinetikus energia. Ez magyarázza, hogy a negatív töltésű elektront nem nyelheti el a pozitív töltésű atommag, noha nulla távolságban lenne a legkisebb a potenciális energia (határértékben negatív végtelen lenne!): kis távolságokban a potenciális energia csökkenését meghaladja a bizonytalansági elvből következő kinetikus energianövekedés. Emiatt kötött állapotban az elektron az atommagtól számítva véges távolságban végzi mozgását, az átlagos távolság hidrogén atomban a Bohr sugár. Mivel az r = 0 határeset kizárható, így a log(r) kifejezéssel arányos lokális entrópia sem vesz fel abszolút értékben végtelenül nagy negatív értéket.

Evolúció az univerzumban

Meggondolásainkban nem korlátozzuk az evolúció fogalmát az élővilág fejlődésére, hanem felhasználjuk az univerzum ősrobbanás utáni állapotainak jellemzésére is. A jelenleg elfogadott elmélet szerint az ősrobbanást követő első időszakban (ez az idő rendkívül rövid, még a részecske fizikában szokásos rendkívül rövid (10^-23s) időnél is rövidebb) Ekkor az univerzum kvarkokból és gluonokból álló plazma volt. Ebben a szakaszban olyan magas volt a hőmérséklet illetve a kvarkok kinetikus energiája, hogy az ütközések szétverték a kvarkokból felépülő elemi részecskéket. Az ősrobbanást követő tágulás – az ideális gázokhoz hasonlóan – fokozatosan csökkentette az univerzum hőmérsékletét, és eljutott arra a pontra, amikor már az ütközések kinetikus energiája nem vetette szét az elemi részecskéket, mint például a hosszú élettartamú protonokat és neutronokat. Ez volt az első fontos minőségi ugrás az univerzum történetében: az egyszerűbb objektumokból összeálltak az első összetett objektumok. Az univerzum teljes entrópiája növekszik, mert a hőmérséklet gyorsabban csökken, mint a termikus energia, viszont lokálisan kialakulnak összetett struktúrák, melyekhez kisebb entrópia tartozik. Tehát az univerzum tágulása indíthatja el az evolúciót.

Az evolúció következő lépcsőfokán a tágulás miatt tovább csökkenő hőmérséklet megengedi, hogy az atommaggá összeépülő protonok és neutronok a termikus ütközések ellenére együtt maradjanak. A nagyobb rendszámú atommagok felépítése azonban nem egyszerű folyamat, mert a pozitív töltésű protonok taszítják egymást, ezért az egyesítéshez át kell lépni a taszítás miatt fellépő magas potenciálgátat. Ebben kap szerepet a gravitáció, amelyik sok-sok nagyságrenddel gyengébb ugyan, mint az elektromágneses erők, vagy különösen az elemi részecskékben és az atommagokban működő erős kölcsönhatás, de a gravitáció mindig vonzást hoz létre és összeadódik szemben a pozitív és negatív töltések egymást kompenzáló hatásával, ugyanakkor nagy távolságokban is hat szemben a magerők rendkívül rövid hatótávolságával. Az óriási tömegű csillagokban a gravitációs nyomás felizzítja a csillagokat és beindul a magfúzió, melynek során létrejönnek a közepes rendszámú elemek. De bizonyos tömegméret felett a csillag elveszíti stabilitását és szupernóvává válik. Ez a robbanás felelős a nehéz elemek kialakulásáért. A harmadik evolúciós fokozat az atomok létrejötte, amikor a pozitív töltésű atommagok körül kialakul az elektronfelhő. Az evolúció, azaz a még összetettebb formációk létrejötte nem áll meg ezen a fokon, mert a lehűlő univerzumban kialakulnak azok a bolygók, ahol az elektronok akkor találják meg a kisebb energiájú pályákat, ha az atomokat molekulákká kovácsolják össze. További lépcsőfok, amikor a molekulák is összetapadnak és folyadékokat, szilárd testeket hoznak létre.

Magyarázhatja-e a fizika az élet keletkezését és a tudat kialakulását?

Eddig a pontig viszonylag könnyű az univerzum evolúcióját magyarázni, mint amit a tágulás miatt képződő lokális entrópia csökkenés hozott létre, de mi vezetett az önszerveződő élet kialakulásához, miért jutott el az evolúció a tudattal rendelkező emberi lény megalkotásáig? Vajon elegendő magyarázatot adhat erre a puszta véletlen, a természet kimeríthetetlen kísérletező kedve? Milliárdnyi galaxis mindegyikében milliárdnyi csillag van, talán ennél is nagyobb a bolygórendszerek száma. Ez esélyt ad arra, hogy létre jöjjenek az élet keletkezéséhez szükséges rendkívül szerencsés körülmények. Az élethez szükséges alapvegyületek, az aminosavak létre jöhettek, ezt megerősítik csillagászati megfigyelések is, de minek köszönhető az első nagy lépés ebbe az irányba? Mondhatunk-e többet annál, hogy a természetben minden megvalósul, ami megvalósítható? Egyáltalán várható-e, hogy a fizika megadhatja erre a kérdésre a választ? Valószínűleg nem, mert a fizikai megismerés határai korlátozottak, az összetettebb struktúráknak megvannak az öntörvényei, amelyek nem vezethetők le a struktúra elemeiből bármennyire alaposan ismerjük is őket. Erre példát találunk a fizikán belül is, ha összevetjük a termodinamika törvényeit az elemi részecskék és atomok mozgását leíró kvantummechanikával. A fizika törvényei szigorúan megszabott körülmények között érvényesek, mindig el kell tekinteni bizonyos kölcsönhatásoktól. De mi van akkor, ha épp az, amit elhanyagolunk a lényeg? Az élő szervezet bonyolult hierarchiája nem érthető meg, ha azt szétbontjuk alkotó elemeire. Ugyanakkor a biológia sokat köszönhet a fizikának és a kémiának, mert rávilágítanak a bonyolult folyamatok elemi lépéseire, de az élő szervezet több annál, mint amit a fizikai és kémiai ismeretek alapján megtudhatunk. Az ember, a tudat megjelenése is egy olyan ugrás, amit nem magyaráz meg önmagában a biológia és az életformák evolúciója. Viszont a fizika adhat egyfajta kiindulópontot, ami alapjául szolgálhat a biológiának, amikor vizsgálja az élet keletkezését, illetve összegezheti különböző okok együttes hatását, de az emberi tudat kialakulásának megértéséhez talán még ennél is feljebb kell lépni – oda, ami már meghaladja a tudomány határait.

Az élő szervezetek felgyorsítják a globális entrópia növekedését

Gondolatmenetemet a fizika világára korlátozva kifejtek egy hipotézist az élet szerveződési formája és az entrópia kapcsolatáról. Az entrópiáról annyit állíthatunk biztosan, hogy az univerzumban – ha azt zárt rendszernek tekintjük – állandóan növekszik, vagy más szóval a természet a nagyobb valószínűségű, a többféleképen megvalósuló állapot felé halad, és a táguló világban ez együtt jár olyan szigetek kialakulásával, ahol viszont lokálisan csökken az entrópia. Ebből még nem következik, hogy az entrópia növekedésnek éppen milyen az útja, és ha többféle út áll rendelkezésre, akkor melyik utat választja a természet, akár lokálisan, akár a teljes univerzum szintjén. Erre vonatkozóan teszek egy hipotézist, amelyik kijelöl egy irányt anélkül, hogy megszabná milyen magasabb szintű okok vezettek az élet kialakulásához: a természet azt az utat választja, amelyik az entrópia leggyorsabb növekedését hozza magával. Másképp fogalmazva: a különböző szintű okok eredőjeként felgyorsul a globális entrópia növekedése. Ezt a hipotézist felfoghatjuk, mint a termodinamika negyedig főtételét, megjegyezve, hogy a harmadik főtétel szintén a perpetuum mobilére vonatkozik, amely megtiltja, hogy ilyen szerkezet akár abszolút zérus fokon is működjék. Amikor már létrejöttek azok a szerves vegyületek, aminosavak, amelyek megfelelő körülmények között létrehozhattak olyan önszerveződő struktúrákat, amelyek már rendelkeztek az alapvető életfunkciókkal, ezek a szervezetek az anyagcsere és egyéb élettani folyamatok révén felgyorsították a globális entrópia növekedését. Akár növényekről, akár állatokról van szó az anyagcsere, a fotoszintézis, vagy a lélegzés olyan átalakítások hosszú-hosszú sorozata, amely összességében jóval több entrópiát termel, mint azaz entrópia csökkenés, ami bekövetkezik az élő szervezet felépítése, fenntartása és szaporítása alkalmából. Az evolúció menete arra vezet, hogy egyre bonyolultabb, egyre összetettebb életformák alakulnak ki, de amelyek egyúttal fokozottabb entrópia termelést valósítanak meg az életfolyamatokon keresztül. Ebben is minőségi ugrást jelent a tudattal bíró ember megjelenése, mert nincs olyan élőlény a Földön, amely hozzá hasonló mértékben termeli az entrópiát saját élete, tevékenysége által. Az emberi társadalom fejlődése is felfogható az egyre nagyobb mérvű entrópia termelés korszakaiként. Ma már az ipari méretekben halmozódó entrópia korszakában élünk veszélyeztetve a Föld ökológiai egyensúlyát is.

Lehet-e szerepe az entrópiának a spontán kvantumugrásokban – A bétabomlás rejtélye és a Higgs-bozon

Befejezésül még néhány gondolat arról, hogy az entrópia, amelyik meghatározza a makroszkopikus folyamatok irányát, mondhat-e bármit a mikroszkopikus folyamatokról, magyarázhatja-e hogy miért következnek be spontán átalakulások az elemi részecskék, vagy az atomok állapotában? A mikrovilág mozgástörvényeit a kvantummechanika írja le. Ebben a leírásban a valószínűség fogalma központi szerepet játszik. Ez a valószínűség azonban alapvetően különbözik attól, ahogy ezt a fogalmat használjuk a termodinamikában folyadékok, vagy gázok tulajdonságainak leírására. Hasonlítsuk össze például, hogyan szökik ki egy molekula a forrásban lévő vízből az atomok és elemi részecskék spontán folyamataival. Ilyen folyamat az elektron emissziója valamilyen radioaktív mag bétabomlásakor, vagy a foton emissziója, amikor az atom vagy molekula elektronrendszere egy gerjesztett állapotból az alapállapotba ugrik. A forrásban lévő víz molekulái nagy sebességgel ütköznek, és előfordul, hogy egy-egy molekula elegendően nagy impulzust és energiát kap, amelyik ennek hatására kiszökik a folyadékból a gáztérbe. A nagyszámú molekuláris ütközés miatt nem tudjuk megmondani, hogy az adott pillanatban éppen melyik molekulával történik ez meg, csak statisztikailag tudjuk jellemezni, hogy adott idő alatt hány vízmolekula hagyja el a folyadékot. Azért használjuk a statisztikai valószínűség fogalmát, mert nem rendelkezünk információval az egyedi molekulák mozgásáról. Evvel szemben nézzük például a radiokarbon, a ¹⁴C mag bomlását. Ennek felezési ideje 5730 év, bármely anyagban, bármilyen körülmények között ennyi időre van szükség, hogy a ¹⁴C szén izotópok fele ¹⁴N atommaggá alakuljon át egy elektron és egy neutrínó kibocsátása mellett. A külső körülményektől független felezési idő azt mutatja, hogy az átalakulást nem a radiokarbon külső környezettel való kölcsönhatása okozza, eltérően a forrásban lévő víz molekuláitól. Gondolhatnánk, hogy a ¹⁴C szén izotópok nyolc neutronjának és hat protonjának véletlenszerű ütközései vezetnek az egyik neutron bétabomlásához. De ennek éppen az ellenkezője igaz, mert a szabad neutron önmagában is felbomlik, sőt sokkal gyorsabban, ekkor a felezési idő csupán tizenöt perc. Amikor szabad neutronokat vizsgálunk, nem tudhatjuk, hogy egy kiválasztott példány mikor fog bomlani, lehet, hogy azonnal, lehet, hogy egy óra, egy nap vagy akár egy év után. Csak azt tudjuk, ha elég sok részecskét figyelünk meg, akkor negyedóra alatt a neutronok fele fog átalakulni protonná. Tehát minden egyes neutronra önálló valószínűségi törvény vonatkozik. Ebből arra következtethetünk, hogy a neutronok és protonok összetett struktúrák, ami megfelel a ma általánosan elfogadott kvark elméletnek, amely szerint a nukleonok három tört töltésű kvarkból állnak, a neutronban két -1/3e töltésű „d” és egy 2/3e töltésű „u” kvark van, míg a protonban a két kvark aránya fordított. A töltések így adják ki a neutron töltéssemlegességét és a proton +e töltését. A neutron bétabomlása során tehát az egyik „d” kvark átalakul „u” formába, amit egy elektron és egy neutrínó kibocsátása kísér. A fizika minden elmozduláshoz, minden átalakuláshoz valamilyen erőt rendel, a bétabomlás hajtó ereje a gyenge kölcsönhatás nevet kapta, amelynek tulajdonságai sokban eltérnek a korábban említett három (gravitáció, elektromágneses és erős) kölcsönhatástól. A bétabomlásban az a legmeglepőbb, hogy a kétlépcsős folyamat első szakaszában létrejön az elektron töltésével rendelkező és a neutronnál közel százszor nagyobb tömegű W^- bozon. (A bozon elnevezés az elemi részecskék egész számmal jellemzett spinjére utal megkülönböztetve a fermionoktól (elektron, proton, neutron, neutrínó), ahol a spin értéke ½ , 3/2 … un. fél-egész szám. A spin definíciójával itt nem foglalkozunk, csak annyit említünk meg, hogy a spinnel kapcsolatosak az elemi részecskék mágneses tulajdonságai és bizonyos statisztikai jellemzők.) Rendkívül meglepő ez az óriási tömeg, hiszen hogyan bocsáthat ki az átalakulásakor a neutron a sajátját közel százszor meghaladó tömegű részecskét? A tömeghez is energia tartozik a jól ismert m.c² összefüggés szerint (itt c a fénysebesség). Az energiamegmaradás tétele szerint viszont valahonnan származnia kell ennek az energiának. A választ Higgs hipotézise adta meg, aki a tér szimmetriatörésére vezette vissza a dolgot, feltételezve egy eddig ismeretlen nagy tömegű bozont, amit később róla neveztek el. Újabban nagy publicitást kapott a nagy energiájú LHC (Large Hadron Collider) gyorsítóval végzett kísérlet, amelyben egy olyan új nagytömegű részecskét sikerült kimutatni, amelynek tulajdonságai valószínűleg megegyeznek (ez egyelőre még nem bizonyított) a Higgs által megjósolt részecskével. Nézetem szerint a tér szimmetriatöréséhez is lehet rendelni entrópiát. A jelenséget úgy szokták szemléltetni, hogy a térnek van egy metastabil szimmetrikus állapota, amiből átmegy egy stabilabb alacsonyabb szimmetriájú állapotba, mintha egy mexikói kalap tetején és annak is a közepén helyeznénk el egy golyót, amelyik körkörösen bármelyik irányba legurulhat. Fent középen magas a szimmetria és ez a helyzet csak egyféleképp valósulhat meg, a legurulás már kiválaszt egy speciális irányt, de ez az irány már sokféle lehet. Ez pontosan annak felel meg, hogy a spontán folyamat a nagyobb entrópiájú állapot felé halad. A gyenge kölcsönhatás tehát a priori entrópia növelő erő, szemben a különböző vonzó kölcsönhatásokkal, amelyek lokálisan csökkentik az entrópiát a kötött állapotok létrehozásával. A bétabomlás entrópia növelő hatását másképp is értelmezhetjük: ennek folyamán egy részecskéből (neutron) három részecske szakad ki (proton, elektron, neutrínó), viszont három részecske téreloszlása sokkal többféle lehet, mint egyetlené, vagyis ebben az értelemben is entrópia növelő folyamatról van szó.

Végezetül néhány szó az elektronok spontán állapotváltozásáról atomokban és molekulákban. A kvantumfizika fontos megállapítása, hogy az atommagok körül kötött elektronok különböző pályán helyezkednek el, úgy nevezett héjakon, de a pályák energiája nem folytonosan, hanem diszkrét módon változik. Emiatt az elektron a kisebb energiájú pályákra nem eshet le, mint az alma a fáról, hanem ugrásokon keresztül jut el. Ez az ugrás spontán módon is végbemehet valamekkora valószínűséggel, de hogy az ugrás éppen mikor történik meg, arra ugyanúgy csak valószínűségi megállapításokat tehetünk, ahogy azt a bétabomlásnál említettük. Az elektronugrás valamelyik alacsonyabb energiájú állapotba foton kibocsátással történik. Ez azt jelenti, hogy az ugrás részecskeszám növekedéssel jár, amit szintén értelmezhetünk entrópia növekedésként. Összefoglalva tehát megfogalmazható a hipotézis, hogy a spontán mikroszkopikus folyamatok irányát meghatározó hajtóerő egyfajta mikroszkopikus entrópiához kapcsolódik.

Összefoglaló gondolatok

                Avval kezdtük, hogy a múltba nem lehet visszatérni és addig jutottunk el, hogy e-mögött az entrópia növekedés folyamata húzódik meg. Az entrópia tehát az a fizikai fogalom, amelyik a mikroszkopikus világtól a makroszkopikusig, az élettelentől az élőig, a tudattal nem rendelkezőtől a tudatig irányt mutat. Az entrópia határozza meg az energiaátalakulások irányát. Az entrópia kapcsolatba hozható az evolúcióval, mert az univerzum tágulása létrehozza az entrópia csökkenés szigeteit, ahol az összetettebb, magasabban szervezett struktúrák kialakulnak. Az evolúció okai szerteágaznak, melyek egy részét ismerjük, más részét viszont nem – de bármelyek legyenek is az okok – az evolúció menetében alapvető szerepe lehet az entrópia gyorsuló ütemű képződésének.

A blog további begyzéseinek összefoglalóját lásd "Paradigmaváltás a fizikában"