Miért éppen operátorok reprezentálják a fizikai mennyiségeket?

 Hogyan lesz a klasszikus fizika p = m.u = m.dx/dt impulzusából a  operátor? Ha ezt megértjük, akkor már nem lesz olyan rejtélyes a kvantummechanika. Newton óta a fizika differenciálegyenletekkel dolgozik. Ennek oka, hogy amikor a legkülönbözőbb fizikai mennyiségek kapcsolatát keressük, akkor arra törekszünk, hogy közöttük az összefüggések lineárisak legyenek. Amikor a változások széles tartományt ölelnek át a jelenség bonyolulttá válik, de ha csupán a fizikai paraméterek parányi változását vizsgáljuk, akkor már elegendő a lineáris közelítés. A nagyobb változásokat ezután már integrálással határozhatjuk meg. Erre példa az elektrodinamika négy alapegyenlete, a Maxwell egyenletek, ahol az elektromos és mágneses mező, valamint a töltések és áramok differenciális kapcsolatát leíró négy egyenlet látványosan egyszerű. de ugyanez elmondható a termodinamikára is. Persze ezek megértése sem könnyű, mert tisztában kell lennünk a vektorok és skalármennyiségek közötti differenciálok matematikájával, de ha evvel megbirkóztunk, akkor kitűnő eszközhöz jutunk a jelenségek leírására.

Ahhoz hogy kezelhető differenciálegyenletekhez jussunk, olyan függvénykapcsolatokra van szükség a fizikai mennyiségek között, amelyek folytonosak és differenciálhatóak. Nem is volt evvel baj a klasszikus fizikában, de amikor kiderült, hogy az elektron energiája ugrásszerűen és nem folytonosan változik az atomi kötött állapotban, akkor nyilvánvalóvá vált, hogy új matematikai eszközökre van szükség. A fizikusok szerencséje, hogy rendelkezésre áll a matematika kincseskamrája, ahonnan sikerült előbányászni az operátorszámítás technikáját. A matematika egyik fő módszere az „emeletráépítés”. Így jön létre az ismételt összeadásból a szorzás, az ismételt szorzásból a hatványozás művelete. A függvény mindig hozzárendelés, amikor egy számhoz egy másik számot rendelünk, de ez a hozzárendelés is tovább építhető, amikor az egyik függvényhez egy másikat rendelünk hozzá. Az a műveleti utasítás, amelyik ezt megteszi az operátor, ez a funkció már a hozzárendelések hozzárendelése.

A függvények és operátorok eltérő szerepének megvilágításához induljunk ki az energia fogalmából. A klasszikus mechanikában az energia az a mennyiség, amelyik a mozgás során nem változik. Ez voltaképpen az energia definíciója. Nézzük például a bolygómozgásokat és egyszerűsítsük a képet körpályákra, amit egyetlen paraméterrel a Naptól való r távolsággal jellemezhetünk. Az energia ekkor a pályát jellemző r sugárral van függvénykapcsolatban:

E(r) = –½γ.M.m/r

Amikor az energiát operátorral írjuk le megváltozik a szemléletmódunk, ettől kezdve úgy tekintünk erre a mennyiségre, mint ami nem változtatja meg a pályát leíró függvényt! Ezt a szemléletmódot a Noether elv fejezi ki, aki úgy értelmezte az energiát, amely független az idő kezdőpontjának megválasztásától. Az időbeli függetlenséghez viszont a d/dt operátor segítségével juthatunk el.

Az operátor formalizmusban két dolgot is keresünk: egyrészt a matematikai műveleti utasítást az energia számára, másrészt egy függvényt, amelyik jellemzi az objektum pályáját! Amikor valamilyen változóval szemben vizsgáljuk az állandóságot – például a d/dt műveletet alkalmazzuk – és függvényekkel írjuk le a fizikai mennyiségeket, az a megoldás kritériuma, hogy differenciálhányados legyen nulla. Az operátor formalizmusban e helyébe lép annak keresése, hogy az operátor hatására a függvény önmagába transzformálódjon. Ez valósul meg, amikor a függvény változatlan marad egyetlen konstans szorzó kivételével. Az ilyen speciális függvényt nevezik az adott operátor sajátfüggvényének és a konstans szorzó lesz az operátor sajátértéke. Az operátorok ez a tulajdonsága lehetőséget kínál a kettős feladat teljesítésére, mert a sajátértéket rendelhetjük az energiához, a sajátfüggvényt pedig a pályához. Ezek a sajátértékek már felvehetnek diszkrét értékeket is, miközben a hozzá tartozó függvények folytonosak és differenciálhatóak lesznek, és így nem veszítjük el a matematikai kezelhetőség előnyeit.

A d/dt operátor sajátfüggvénye az exponenciális függvény:

d/dt exp(n.t) = n.exp(n.t)

Ekkor n a sajátérték és exp(n.t) a sajátfüggvény. Ez a választás még nem felel meg az energiának, mert egyrészt az n érték folytonosan változik és így nem kapunk diszkrét energiákat, másrészt az exp(n.t) függvény nem alkalmas a mozgási pálya leírására, mert a t→∞ határesetben a végtelenbe fut, mi viszont térben és időben véges pályákat keresünk. Segít a dolgon, ha az exponens imaginárius, és tegyük az exponenst dimenzió mentessé a frekvencia dimenziójú ω bevezetésével: exp(i.ω.t). Ekkor a sajátérték i.ω imaginárius lesz, mi viszont az energiára csak valós mennyiségeket adhatunk meg, ami megköveteli, hogy az operátor imaginárius legyen, mert így a sajátérték valós szám lesz. További feltétel, hogy a sajátérték dimenziója energia egységekben jelenjen meg, amit úgy érünk el, ha impulzusmomentum dimenziójú konstanssal szorozzuk meg az i(d/dt) operátort. Hogyan válasszuk meg ezt a konstanst? Ebben segít a foton E = ℏ.ω energiája, ami a fekete test sugárzásának energia eloszlásából következik. Nekünk ugyanis olyan energia operátorra van szükségünk, amelyik egyaránt alkalmazható valamennyi elemi részecske leírására beleértve a fotonokat és elektronokat is. Így jutunk el az energia operátorához: ℏ.i(d/dt), míg a hozzá tartozó sajátfüggvényeket az ω körfrekvenciájú időben periodikus függvények képezik.

Még nem beszéltünk a pályafüggvény térbeli szerkezetéről, amit az energia két összetevőjéből: a mozgási (kinetikus)  és az erőhatás miatti (potenciális) tagjából kaphatunk meg. A kinetikus energia az impulzustól származik. Az impulzus operátor megtalálásához is a Noether-elv vezet, amelyik úgy definiálja ezt a mozgási állandót, melynek értéke nem függ attól, hogy hová helyezzük el a koordináta rendszer kezdőpontját, például az x irányban az x₀ pontot. Ehhez a ∂/∂x művelet tartozik. Az impulzus exponenciális sajátfüggvényének végessége itt is megkívánja, hogy az operátor imaginárius legyen, a foton p = ℏ.ω/c impulzusát pedig az biztosítja, ha a ℏ konstanssal szorzunk. Következésképp az impulzus x komponensének operátora

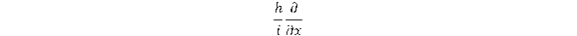
Az y és z irányú komponens ennek megfelelően írható fel. Az operátorban konvenciószerűen az imaginárius egység a nevezőben szerepel, mert ez biztosítja az impulzus sajátértékek pozitív előjelét. Az energiánál az „i” a számlálóban van, ami negatív energiát biztosít a kötött elektronok esetében összhangban a klasszikus konvencióval.

Elektron stacionárius állapotban: a pálya időfüggésének elvesztése

A kinetikus energiát p²/2m definícióval megadva és hozzávéve a potenciális energiát már eljutunk az elektron nem-relativisztikus Schrödinger-egyenletéhez

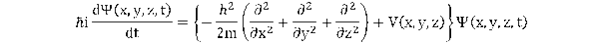
Az elektron energiáját időtől nem függő potenciáltérben vizsgáljuk, például legyen az elektron egy atomban. A differenciálegyenletben ekkor szeparálható a tér és az időfüggés, így a hullámfüggvény szorzatalakban kereshető ψ = Φ(x,y,z).φ(t). Az egyenlet jobb oldalán szereplő energiaoperátor, a Hamilton operátor sajátérték egyenlete adja meg a hullámfüggvény térfüggő részét:

H.Φ_n,k(x,y,z) = E_n .Φ_n,k(x,y,z)

Az energia sajátfüggvényét nevezzük állapotfüggvénynek, mert ez egyértelműen definiálja a kvantummechanikai rendszer stacionárius állapotát. Ez azt jelenti, hogy az állapotfüggvény segítségével a rendszer minden fizikai tulajdonsága megadható. Itt két indexet használtunk, az n index különbözteti meg a különböző energiájú állapotokat, de ugyanakkora energiához több függvény is tartozhat, amit a k  indexszel jelölünk.

Az a matematikai eszköz, amivel eljutunk az egyes fizikai paraméterek értékéhez a függvények skalárszorzása, ami egy olyan integrálási művelet, amelyben megszorozzuk a függvényt egy másik függvény komplex konjugáltjával és kiterjesztjük az integrált az egész x,y,z térre. Mindig normált függvényeket használunk, mert a normálás biztosítja a számítások egyértelműségét, emellett további követelmény, hogy a különböző állapotokat leíró függvények skalárszorzata nulla legyen (ortogonalitás):

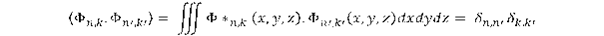
A fenti Kronecker delta egy, ha egyeznek az indexek, egyébként nulla.

A fizikai operátorok értékét, például az impulzus x komponensét, a következő skalárszorzat adja meg::

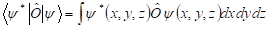
Itt a k indexre nincs szükség, mert az azonos energiához tartozó állapotokban (eltekintve a véletlen degenerációtól) minden fizikai paraméter értéke megegyezik. Ha a Φ_n függvény egyúttal az impulzus operátornak is sajátfüggvénye, akkor az impulzus pontos értékkel rendelkezik. Ellenkező esetben csak az impulzus várható értékéről beszélhetünk.

Az elektronpályát valószínűség eloszlásként írjuk le, amit a tér az r = (x,y,z) pontjában az állapotfüggvény abszolút értékének négyzete, azaz Φ*(x,y,z)Φ(x,y,z), határoz meg. Az eloszlási függvénynek a tér koordináták szerinti integrálja az egység, ami azt fejezi ki, hogy az egész térben egységnyi valószínűséggel (tehát biztosan) megtaláljuk az elektront, a Φ(x,y,z) függvényt pedig úgy értelmezzük mint valószínűségi amplitúdót.

Vessük össze az elektronpályának kvantummechanikai leírását a klasszikus mechanika pálya fogalmával. Az utóbbiban a fizikai objektum pályáját valamilyen r(t) függvény írja le és ebből a pályából származtathatjuk az objektum impulzusának, gyorsulásának és energiájának időbeli változását. Evvel szemben a kvantummechanikai leírás egyrészt nem számol be időfüggésről, másrészt csak valószínűségi kijelentést tesz a részecske térbeli helyzetéről.

Az időtől független potenciáltérben jönnek létre az elektron stacionárius állapotai, amikor a hullámfüggvény térfüggő részéről leválasztható az időfüggés. Az ennek megfelelő elektronpályákat már nem a szokásos téridő koordináták írják le, ekkor az idő helyébe lép a valószínűség fogalma, ezt úgy is mondhatjuk, hogy az atomban az elektron nem „kering”, hanem „eloszlik”. Emiatt másképp kell gondolnunk az impulzusra is, mert az idő hiányában a sebesség – és ezáltal az impulzus – értelmetlenné válik. Ha nincs sebesség, akkor gyorsulás sincs, ezért nem sugároz az atom stacionárius állapotban!

Kötött állapotban az impulzus várható értéke nulla, hiszen ellenkező esetben az elektron elmasírozna az atomból. Nem vethetjük viszont fel a kérdést, hogy a tér (x,y,z) pontjában  mekkora az impulzus értéke. Ez úgy jelenik meg a kvantummechanikai formalizmusban, hogy ebben a pontban az impulzus tisztán imaginárius lesz, azaz nincs fizikai tartalma. A valószínűségi eloszlás miatt viszont beszélhetünk az impulzus statisztikai szórásáról, azaz a <p²> várható értékéről, ami tulajdonképp a kinetikus energiának felel meg, hiszen E_kin = ½ p²/m. Amíg a klasszikus fizikában a kinetikus energiát az objektum sebessége, addig stacionárius állapotban térbeli eloszlása határozza meg.

Hogyan magyarázzuk meg az eltérő pályafogalmat, vajon csak elméleti műtermékről van szó, vagy a mikrovilág objektumai tényleg másképp viselkednek? Tulajdonképpen ezt a kérdést veti fel az Einstein, Podolsky és Rosen által felvetett paradoxon is, akik rejtett paraméterekkel kívánták kibővíteni a kvantummechanikát a folyamatok determinisztikus leírása érdekében. Az „EPR paradoxon” című bejegyzésben erről részletesen szó esik.

A magyarázat lényege a mikro folyamatokról szerezhető információ korlátozott mennyisége és minősége. A bolygó mozgásáról, vagy a labda pályájáról rengeteg információt nyerhetünk az objektumtól származó fotonok óriási száma miatt és fel sem merül bennünk, hogy a megfigyeléshez használt eszközök és a vizsgált objektumok közötti kölcsönhatás megváltoztatná a bolygó, vagy a labda pályáját. Emiatt módunk van az egymást követő képek sorozatából megállapítani az objektum pályáját. Más a helyzet az elektronnal, mert amikor stacionárius pályán tartózkodik semmilyen információnk nincs és nem is lehet a pályájáról, mert minden megfigyelés egy foton kibocsátásával, vagy elnyelésével jár együtt, és ekkor a pálya is megváltozik. Nem tudjuk tehát az elektron mozgását időben nyomon követni, így a kvantummechanikai leírás csak arra szorítkozik, hogy valószínűségi súlyokat adjon a tartózkodási helyről. Amit egyáltalán „látunk” az egy ugrás két pálya között és ezekből az ugrásokból következtetünk arra, hogy milyenek azok a pályák, amelyek között az átmenet végbemegy. A nyerhető információ pontossága is korlátozott a fotonok karakterisztikus tulajdonságai miatt, mert minden átmenethez véges energia (ℏ.ω), véges impulzus (ℏ.ω/c) és véges impulzusmomentum (ℏ) tartozik. A fotonok által nyújtott pozíciómérés pontosságát a c/ω hullámhossz, az impulzusét a ℏ.ω/c „lökés” nagysága korlátozza, ezért jelent végső pontossági határt a Planck állandó, amikor ezt a két mennyiséget kívánjuk egyszerre meghatározni (a két mérési hiba szorzata ℏ).

 A kvantummechanika a fentiek miatt „praktikus” elmélet, csak megválaszolható kérdésekkel foglalkozik, arra viszont jelenlegi tudásunk szerint tökéletes választ tud adni.

A kvantummechanika további sajátossága a szuperpozíció elve. Ha például két állapot ugyanahhoz az energiához tartozik, akkor a két függvény bármilyen szuperpozíciója is ugyanúgy alkalmas az elektron pályájának leírására. Ennek is a korlátozott információ az eredete. Gondoljunk a hidrogén atomra, ahol egyetlen elektron „kering” a proton körül. A pálya impulzusmomentuma szerint különböző számú degenerált energiaállapot létezik, az s pálya (L = 0) egyszeresen, a p pálya (L = 1) háromszorosan, a d pálya (L = 2) ötszörösen degenerált, és ezekből a pályákból tetszőlegesen képzett szuperpozíció egyaránt megfelelő állapotfüggvényeket ad. Ennek oka, hogy a gömbszimmetrikus potenciáltérben mozgó elektron számára nincs „értelme” az iránynak, ebben a fogalomkörben csak „mi” gondolkozunk, mert a makroszkopikus világból nyerjük tapasztalatainkat. A kvantummechanika ezt úgy fogalmazza meg, hogy az állapotfüggvény valószínűségi amplitúdója minden irányban azonos lesz. Ez külön is érvényes a gömbszimmetrikus s pályára, míg a p, d stb. pályák esetén az irányok megkülönböztethetetlensége vezet a szuperpozíció elvéhez.

Az elektron interferencia jelensége 

Nem foglalkoztunk még a Schrödinger egyenlet időtől függő φ(t) függvényével, amit meghatározhatunk az E__n sajátérték ismeretében: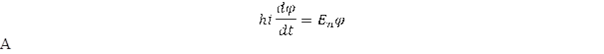

A hullámfüggvény időfüggő része  

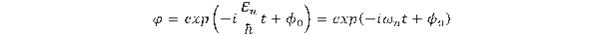
A hullámfüggvény időben periodikus tényezője jellemzi az elektron hullám természetét. Ez összhangban van a kísérletekkel, mely szerint az elektron, sőt az atomok és kisebb molekulák is a fotonhoz hasonlóan interferenciát hoznak létre.

Stacionárius állapotok a kvantumelektrodinamikában 

Az atomi elektronpályákat Bohr még a klasszikus mechanika törvényei alapján vizsgálta. Modelljének kritikus pontja volt, hogy az elektrodinamika szerint a körpályán mozgó elektromos töltésnek a gyorsulás miatt sugározni kell, ami viszont az elektron energiájának fokozatos elvesztését idézné elő. Ez tette szükségessé azt a feltételezést, hogy az elektronok stacionárius pályán nem sugároznak. Később a kvantummechanika ezt igazolta, mert mint korábban láttuk a stacionárius pálya független az időtől, és így nem beszélhetünk gyorsulásról. Hasonlóan alátámasztja ezt az elképzelést a fotonok kvantumos jellege, mert folytonos sugárzás egy gyorsuló töltés esetén csak úgy lehetséges, ha már végtelenül kis energia és impulzusváltozás elegendő a foton kibocsátáshoz.

A kvantummechanikai magyarázat mégsem teljes, mert ha a pályák nem függenek az időtől, akkor mi készteti az elektront, hogy a magasabb energiájú pályáról az alacsonyabbakra átugorjon. Ezt a hiányosságot küszöböli ki a kvantum elektrodinamika, amikor bevezeti a második kvantálás fogalmát. Az elmélet felveti a kérdést, hogy miért vonzza, vagy taszítja egymást két töltés, amelyik egymástól r távolságban van és miért jelentkezik ez a hatás csak r/c idővel később? Ezt a jelenséget a virtuális fotonokkal magyarázza, amelyek egyidejűleg képződnek és elnyelődnek és ezek a virtuális folyamatok közvetítik a kölcsönhatást a részecskék között. Ez létrehozza az elektromos és mágneses mezőt, amelyik azonban „ingadozik” az átlagérték körül és ennek hatása anomális járulékot ad az elektron mágneses momentumához és spontán módon beindítja az elektron átmeneteket. A kísérletileg mért momentum rendkívül jó egyezése a számított értékkel az elmélet legfőbb bizonyítéka. Az elméletnek azonban van egy szépséghibája, mert a részecskék saját energiájára végtelenül nagy értéket ad. Evvel a kérdéssel más helyen foglalkozunk („Nyitott kérdések …”

A blog további bejegyzéseinek összefoglalóját lásd "Paradigmaváltás a fizikában"

Rockenbauer Antal