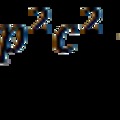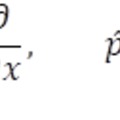Második rész: Az EPR paradoxon

Einstein felfogása a kvantummechanikáról

A bejegyzés első részében azt a kérdést jártuk körül, hogy milyen fordulatokon ment át az általános relativitáselmélet és ez hogyan mutatkozott meg Einstein gondolkozásában. Most egy másik területet veszünk szemügyre a kvantummechanika világát. Einstein mindig fizikai elvekben gondolkozott, ezért számára alapvető volt annak megértése, hogyan fogjuk fel a kvantummechanikai véletlen szerepét, felfogásával ellentétes volt az olyan elmélet, amely tagadja a determinizmust az elemi folyamatokban. Ezeket a nézeteket fejtette ki Podolskyval és Rosennel közös publikációjában (A. Einstein, B. Podolsky and N. Rosen, “Can Quantum-Mechanical Description of Physical Reality be Considered Complete?” Phys. Rev. 47, 777-780 (1935).

Rejtett paraméterek

Az említett publikációban (a továbbiakban EPR) kifejtették azt a nézetüket, hogy a determinizmus hiánya miatt szükség lenne a kvantummechanikát kibővíteni „rejtett” paraméterrel, ami a valószínűségi kép mögött gondoskodna a folyamatok egyértelmű kimenetéről. Ez a kérdés azóta is vita tárgya a szakirodalomban, számos publikáció cáfolja, hogy létezhetnek-e ilyen rejtett paraméterek, de megjelentek Einstein nézetét támogató közlemének is. Azóta is ezt a kérdést mint az EPR paradoxont tárgyalja az irodalom. Itt egy összefoglaló értekezésre is utalok: Guy Blaylock, “The EPR paradox, Bell’s inequality, and the question of locality,” Am. J. Phys. 78 (1), 111-120 (2010).

Gondolatkísérletek 

Nézzük meg, hogy miben is lehetett igaza Einsteinnek és miben tévedett. Korábban már foglalkoztam evvel a kérdéssel (lásd: „Determinizmus és kvantummechanika: a szabadság szintjei a fizikában” és az angol nyelvű „EPR paradoxon”), itt most a kérdést más szemszögből tárgyalom. Einstein módszere a kérdés kiélezése volt különböző gondolatkísérletekkel. Például elképzelte, hogy egy gömb belsejében egy fotonforrást helyezünk el, amelyben szabályozni tudjuk, hogy egyesével lépjenek ki a fotonok. A gömb teljes felületén detektorokat helyezünk el. A kibocsátott foton pályáját gömbfüggvény írja le, amely szerint minden irányban egyenlő valószínűséggel kerülhet sor detektálásra, de végül mégiscsak egyetlen detektor szólalhat meg. Honnan tudja a többi detektor, hogy néma maradjon és mi alapján kerül kiválasztásra szóban forgó detektor? Ehhez kapcsolódik  Einstein gyakran idézett és kritizált kiszólása is: "az Isten nem kockajátékos".

A mikrovilág makroszkopikus vizsgálata 

Először is azt kell végiggondolni, hogyan valósítható meg az előbbi kísérlet. Elvi akadálya nincs, mert a foto-elektronsokszorozóval el tudjuk érni, hogy egyetlen beérkező részecske is detektálásra kerüljön, de természetesen, amit észlelünk, az már makroszkopikus jel. Viszont amikor megállapítjuk, hogy éppen melyik detektor szólalt meg felhasználunk egy fontos kiegészítő információt, hiszen „látjuk”, hogy hol van a detektor. Ez a második pont a lényeg, mert a detektort azért látjuk, mert onnan nagyszámú foton érkezik a szemünkbe. Ugyanez vonatkozik a fotont kibocsátó berendezésre is. E-nélkül a többlet információ nélkül nem tudnánk beszélni az irányról! Tehát az információ nem egyetlen fotontól származik, azaz ebben a tekintetben nem választható szét az egyedi fotonra vonatkozó információ attól, amit makroszkopikusan szerzünk meg a vizsgálathoz használt berendezésről. 

Kétréses kísérletek 

Az előző esetben még gondolhatnánk azt, hogy a fotonok iránya határozza meg, hogy mi történik a részecskével, ekkor a fotonokat korpuszkulának tekintjük. Ez a korpuszkula modell azonban nem alkalmas a kétréses kísérlet értelmezésére.. Ha a gömb felületén két rést nyitunk, és a gömbön kívül elhelyezünk egy fényérzékeny lemezt, akkor a gömb centrumából egyenként indított fotonok bizonyos helyeken gyakrabban, másutt ritkábban hoznak létre elszíneződést, és a maximum és minimum helyek a lemezen periodikusan ismétlődnek. Ez az interferencia jelenség, amit úgy magyarázunk, hogy számításba vesszük az ernyőn a két réstől mért optikai úthosszak különbségét. Ekkor tehát a foton egyidejűleg mindkét résen áthalad és létrehoz egy-egy új gömbhullámot, ami aztán interferenciát produkál. Ezt a viselkedést tekintjük a részecske hullámtermészetének. 

A mikrovilág objektumainak kettős természete 

A hullám és korpuszkuláris természet kettőssége azonban nem csak a fotont jellemzi, megfigyelhető interferencia elektronokkal, protonokkal, sőt kisebb molekulákkal is. Itt az interferencia maximumok távolságát a részecske m tömegéhez rendelhető λ = h/mc Compton hullámhossz adja meg. Ez a hullámhossz megfelel a fénysebességű forgásmodellből származtatható részecske sugárnak a λ = 2πr összefüggés szerint. (Lásd: "Az egységes fizikai világkép" és a  "A fénysebességű forgások és a relativitáselmélet" című írásokat)

A korpuszkuláris tulajdonságokat például a gyorsítókból kibocsátott részecskékkel tanulmányozhatjuk, ha fényérzékeny emulzión halad át a részecske. Ekkor az ionizációs hatás kémia reakciókat idéz elő és ezáltal a részecske pályájának nyomvonalát tanulmányozhatjuk. Ilyenkor is az információt a makroszkopikus megfigyelés teszi lehetővé, részecskét, magát közvetlenül nem láthatjuk, csak az általa létrehozott nyomvonalat. Ebben különbözik az elektron pályája a labdáétól. A labdáról minden pillanatban nagyszámú foton érkezik, és ezáltal láthatjuk, és akár videóra is vehetjük, vagy lefilmezhetjük a pályát. Elektronok esetén erre nincsen mód, például atomokban az állandó (stacionárius) pályán lévő elektron nem bocsát ki megfigyelhető fotonokat, csak akkor szerzünk az elektron pályájáról információt, amikor átugrik az egyik állapotból a másikba. Az atomi pályáról nyert információnk ezért közvetett, csak az ugrások nagyságából (a kibocsátott foton energiájából) számolhatjuk ki, hogy melyik két állapot között történt az átmenet, és az információ pontosságát a foton tulajdonságai szabják meg. (Lásd: Foton: a mikrorendszerek postása és szabályozója). 

A hullámfüggvény redukciója 

Azt a kérdést, hogy a mikro rendszerekről szerezhető információ mindig makroszkopikus megfigyelésekre támaszkodik, azért tartom fontosnak, mert ez segít megérteni a kvantummechanika sokszor félremagyarázott sajátságát. Amikor a mérés előtti állapotot írjuk le, akkor a mikro rendszert olyan hullámfüggvénnyel jellemezzük, amely különböző értékeket enged meg az egyes fizikai paraméterek számára (például a pozíció és impulzus bizonyos valószínűséggel rendelkezik különböző értékekkel), de amikor a mérés bekövetkezik már csak egyetlen érték nyerhető a lehetőségek közül. Ezt nevezi a szakirodalom a hullámfüggvény redukciójának. Sokan, például Penrose is a Hawkinggal folytatott vitájában, erre akarja visszavezetni az agyunk működését is (lásd: Roger Penrose, Stephen Hawking, Abner Shimony, Nancy Cartwright: „A nagy, a kicsi és az emberi elme”, Akkord Kiadó, 2003).  Szerintem viszont csupán arról van szó, hogy a mérés előtti információ korlátozott a mikro rendszerről, amire így csak valószínűségi kijelentéseket tehetünk bizonyos előfeltételek alapján. (Például kiindulhatunk abból, hogy a vizsgált elektron valamilyen ismert molekulában van). A mérést elvégezve már kibővül a mikro rendszerről szerzett információnk és ezt vesszük tudomásul, amikor a hullámfüggvény redukciójáról beszélünk. 

A rejtett paraméter létezésének cáfolata 

Einsteinnek azt a koncepcióját, hogy a kvantummechanikát ki kellene egészíteni valamilyen rejtett paraméterrel többen cáfolták, ennek ma már hosszú irodalma van, amire kitűnő összefoglalást ad Geszti Tamás (lásd: „Kvantummechanika”, Typotex, 2014.). Elsőként Neumann János nevét kell említeni, aki kissé körülményes matematikai bizonyítást adott, a későbbi szakmai irodalom a Bell által felállított egyenlőtlenség alapján mondja ki, hogy olyan rejtett paraméter, amely mindenkoron egyértelmű leírást adna a mikrorendszer állapotára ütközik a kvantummechanika szabályaival. (Lásd: John S. Bell, "On the einstein-podolsky-rosen paradox," Physics 1 (3), 195-200 (1964). Bell ezt az egyidejűleg kibocsátott két részecske (például két foton, vagy egy elektron-pozitron pár) esetén mutatta ki, amikor a kibocsátás helyétől egyenlő távolságban határozzuk meg a részecskék polarizációját különböző kísérleti elrendezésekben (a részleteket lásd Geszti Tamás könyvében). A két mérés várható eredményét összegezve arra az eredményre jutunk a kvantummechanikai törvények alapján, hogy a kibocsátás helyén nem lehet pontosan definiált a részecskék polarizációs értéke. Következésképp Einstein hipotézise hibás, mert a rejtett paraméter jelenléte összeegyeztethetetlen a kvantummechanikával.  

A kvantummechanika fázis kitüntetett szerepe 

Einstein azonban csak részben tévedett. Olyan rejtett paraméter valóban nincs, amelyik minden időpillanatban egyértelműen határozná meg a polarizációs irányt, viszont a hullámfüggvénynek van egy fázisa és ez a fázis éppen ellentétes a két részecske számára. Elvben ez a fázis meghatározhatná a polarizációs irányt is, de nem tudhatjuk, hogy ez milyen irány, mert a részecskék kibocsátási helyén a mérés előtti állapotban az irány fogalmának nincs értelme. Csak akkor beszélhetünk irányról, ha összehasonlításra kerül sor, e-nélkül viszont a mikrorendszerben az irány fiktív. Valóságossá akkor válik az irány, ha a berendezéstől származó fotonok eljutnak a szemünkbe, azaz a mikro rendszerről szerzett információt kibővítjük a makroszkopikus rendszer alapján kapott információval. Amiben viszont nincs igaza Einsteinnek, hogy a rejtett paramétert a kvantummechanikán kívül kereste. A mikro folyamatok eredményét ugyanis a fázis határozza meg, a kvantummechanika amiatt használ valószínűségeket a várható eredmény meghatározására, mert részben, vagy egészben a mikrorendszerek tere és ideje fiktív. 

Schrödinger macskája 

Hasonló gondokozási hiba érhető tetten Schrödingernél is, amikor egy macskával érzékelteti a kvantummechanika szuperponált állapotait. A szuperpozíció azt jelenti, hogy az elektron, vagy a foton bizonyos valószínűséggel lehet egyidejűleg különböző állapotokban. A mérés fogja valamelyik állapotot kiválasztani és ennek eredménye határozza meg, hogy egy méreggel töltött kapszula kinyílik-e és megöli-e a macskát. Mielőtt kinyitnánk azt a zárt dobozt, amiben a macska van, nem tudjuk az eredményt. Schrödinger és követői oly módon tárgyalják a kérdést, hogy az élő illetve a döglött macskaállapotot kvantummechanikai szuperpozíciónak tekintik, más szóval a doboz kinyitása előtti helyzetet az élő és holt állapot szuperpozíciójának tartják, amihez meghatározott valószínűség tartozik. A kép nyilvánvalóan abszurd, csupán úgy lehet felvetni, ha figyelmen kívül hagyjuk, hogy a macska nem mikrorészecske, és emiatt számára a tér és az idő valóságos, nem pedig fiktív. A macska együtt él és lélegzik a környezetével, és ezáltal állandó változásban van, míg az elemi részecskék stacionárius állapotban nem változnak meg semmiben. Más szóval a macska akár él, akár nem, nincs stacionárius állapotban, ezért nem alkalmazhatjuk rá a stacionárius állapotok szuperpozíciós törvényét. 

Interferencia és rezonancia 

Térjünk vissza a fázis szerepére. A hullámok találkozása úgy hozza létre az interferenciát, hogy ahol egyezik két hullám fázisa ott erősítik egymást, ahol ellentétes ott kioltják. A részecskék hullámtermészetének következménye, hogy a foton, az elektron, sőt a nagyobb tömegű atomok és molekulák esetében is megfigyelhető az interferencia. Milyen lehet a fázis szerepe akkor, ha az elektronok és fotonok kölcsönhatásáról van szó? Interferencia ekkor nem jön létre, mert a részecskék frekvenciája eltér egymástól. Létrejön azonban rezonancia, ha a kötött állapotú elektron két állapota között az energiakülönbség ΔE = h.ν, ahol ν a foton frekvenciája. Ez pillanatnyi fázisegyezéssel magyarázható a foton és az elektron között. Hasonlóan értelmezhetjük, hogy az üveglapra beeső fénynek miért 4 százaléka verődik vissza és 96 százaléka megy át az üvegen. Az a foton fog visszaverődni, amelynek fázisa elég közel esik valamelyik elektronhoz. A kvantummechanika nem foglalkozik ilyen esetekben a fázissal, ennek oka, hogy ez a fázis a mérés előtti állapotban mindig ismeretlen, a fizika és ezen belül a kvantummechanika pedig csak avval foglalkozik, ami mérhető. A mikro folyamatok determinizmusa tehát fennáll, de ennek megismerése már meghaladja a fizikai megismerés határait. A mikro folyamatok valószínűségi jellege ezért információnk korlátozottságát tükrözi. 

A korpuszkuláris és hullámtermészet kettőssége úgy értelmezhető a mikro objektumok között, hogy az előbbi esetben egyetlen lökés hozza létre a kölcsönhatást, ha a fázisviszonyok megfelelőek, míg az utóbbi esetben a frekvenciák azonossága szükséges ahhoz, hogy a periodikusan ismétlődő hatás interferenciát okozzon.

Léteznek-e összefonódott kvantumállapotok? 

Térjünk még vissza a kétrészecske problémára, melyek a kezdetben csak gondolatkísérletek voltak, de később megvalósításra kerültek. Először Aspect végzett ilyen kísérletet (lásd: A. Aspect, P. Grangier and G. Roger, "Experimental realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: a new violation of Bell's inequalities,"  Phys. Rev. Lett.  49 (2), 91 (1982))., de vele egyező eredményre jutottak más szerzők is. Az Aspect kísérletben két ellentétes irányban megfigyelt részecske (például egy elektron és pozitron), vagy két foton szerepel, melyeket a kibocsátás helyétől egyenlő távolságban detektálunk. A kísérletek célja az együtt kibocsátott fotonok polarizációs irányának meghatározása. Fotonok polarizációját vizsgálva Aspect és munkatársai azt találták, hogy a két polarizációs állapot, amit egyidejűleg detektáltak éppen ellentétes. A koppenhágai iskola ezt úgy interpretálja, hogy a kibocsátás után is állandó kontaktusban maradnak a fotonok, mintegy „összefonódva” és emiatt, amikor az egyik foton felvesz egy polarizációs irányt, a másik ehhez késlekedés nélkül „igazodik”. Ez a magyarázat viszont azt jelenti, hogy a fotonok közötti információcsere sebessége meghaladná a fény sebességét! De ez csak a fotonok információcseréjét jelenti, a kísérletező erről nem tud, válaszolják erre a koppenhágai iskola követői és bevezetik az összefonódott részecskeállapotok koncepcióját, amely egyetlen egységnek tekinti a két részecskéből álló rendszert. Ez a koncepció a kölcsönhatások nem-lokális jellegének felel meg, azaz nem két pontszerű (vagy szűk térben lokalizált), hanem térben kiterjedt objektumok kölcsönhatásáról van szó.

A valódi magyarázatot a fotonok fáziskoherenciája adja meg. A megmaradási törvények miatt az együtt képződő két foton fázisa ellentétes lesz, és ez megőrződik a továbbiakban is a frekvenciák azonossága miatt. Tehát nem tudjuk ugyan, hogy mi a kezdeti fázis a fotonok kibocsátásakor, de abban biztosak lehetünk, hogy a fázisok különbsége nem változik. Nincs szükség tehát elméleteket konstruálni az összefonódó fotonokról, vagy más részecskékről!

Einstein munkásságának tanulságai 

Bár Einsteinnek csak részben volt igaza, a problémafelvetés mégis serkentően hatott a fizika fejlődésére Ez is jó példa rá, hogy a kutatónak bátran vállalni kell a tévedés kockázatát is. De szólnunk kell még Einstein utolsó évtizedeiről is, ami nem hozott már új eredményeket. Ennek okát abban látom, hogy nem folytatta azt az utat, amit az általános relativitáselmélet megfogalmazásakor elkezdett. Amikor kereste a gravitáció elméletének összekapcsolását az elektromágnesességgel, akkor nem a téridő szerkezetéből indult ki, hanem a kvantumelvből. Pedig a kvantum, ahogyan én látom (lásd: „A kvantumelv határai a fizikában”), nem a mikrovilág végső építőköve. Ez is csak egy megnyilvánulása a fénysebességű forgásoknak, ami extrém geometriai torzulást hoz létre a téridőben. Ha innen indulunk el, akkor természetes kapcsolatot találunk a fizika különböző kölcsönhatásai között. 

További bejegyzések összefoglalását lásd „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”