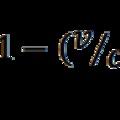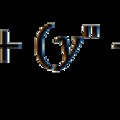Lehetséges-e a csillagközi utazás?
A csillagközi utazás az emberiség nagy álma lehetne, de van-e erre esély, vajon nem ellenkezik ez a fizika, de még inkább az élet törvényeivel? Evvel a kérdéssel foglalkozom a fizikában tett újabb kalandozásban. Egy ilyen kalandra leginkább az Alfa Centauri lehetne alkalmas, mert „mindössze” 4,3 fényévnyire van a mi Naprendszerünktől. A fény tehát 8,6 év alatt megteheti oda-vissza az utat, de mennyi időre lenne szüksége egy ember által irányított űrhajónak?
Az Alfa Centauri már többeknek is felkeltette érdeklődését, így Stephen Hawking javasolta, hogy el lehetne küldeni oda egy vitorlával felszerelt dront, amit lézer sugárral lehetne felgyorsítani megfelelő sebességre. Ez már ésszerű idő alatt megérkezhetne és üzenetet küldene vissza onnan, bár visszatérése nem lenne megoldható. Az űrtechnika szokásos eszközeivel beláthatatlanul hosszú időbe telne (30 ezer év) eljuttatni bármilyen űreszközt oda. A sci-fi irodalom kedvenc ötlete a „féreglyukon” való átlépés egy távoli világba, de még ha tényleg fennáll ez a relativitáselméletből következő lehetőség, a gravitációs viszonyok összezúznának minden életet, sőt objektumot is. Maradjon meg ez a lehetőség ezért a fantázia birodalmában és foglalkozzunk inkább avval, milyen törvényeket kell figyelembe venni, ha évtizedes távlatokban képzelünk el egy űrutazást.
Miért nem alkalmas a rakétatechnika a csillagközi utazásra?
A szokásos rakétatechnika nem lenne alkalmazható több okból sem. Egyrészt a fénysebesség közelébe csak úgy juthatnánk el, ha hosszú ideig a földi gravitáció sokszorosával gyorsulna fel az űrkabin, amit már nem viselne el az emberi szervezet, de a fő kérdés, hogyan lassulna vissza az űrhajó a megérkezéskor és hogyan jönne vissza? Ezért olyan megoldás kellene, ahol az űrhajó állandóan gyorsul, mégpedig az emberi élet szempontjából kedvező 1 g (10 m/s2) gyorsulással. Ez egyúttal megoldaná a súlytalanság állapotában bekövetkező fizikai leépülés problémáját is, hiszen az űrhajósok a földivel azonos erőhatásnak lennénk kitéve. Az utazás első felében gyorsulna, majd félúton megfordulna a hajó és ekkor a sugárhajtóművek 1g –vel már lassítanák az űrhajót, amíg megérkezne a kitűzött tartományba az Alfa Centauri körül. Innen indulhatna vissza az űrhajó először gyorsulva a Föld felé, majd félúton jönne az utolsó lassulási szakasz. A kérdés, hogy mennyi ideig tartana ez az út és mennyi, illetve milyen „üzemanyagra” lenne ehhez szükség. Mint látni fogjuk az utóbbi okozza az igazi problémát, de nézzük meg először az idő kérdését.
Mennyi idő kell az utazáshoz 1 g gyorsulással?
Az egész példát azért választottam, mert kitűnően alkalmas a relativisztikus hatások szemléltetésére és ezáltal az olvasó közelebb kerülhet ehhez a különös világhoz. Nézzük először a megteendő utat. A fény egy év, azaz 365x24x3600 = 31,6 millió másodperc alatt, 9,48x1015 métert tesz meg (a fénysebesség c = 3x108 m/s), azaz az Alfa Centauri távolsága mintegy 4x1016 m. Számítsuk ki azt az időt, ami ennek feléhez (2x1016 m) kell, mert eddig fog gyorsulni az űrhajó. Ha nem vesszük figyelembe a relativisztikus hatást, akkor az út és idő kapcsolatát az s = ½gt2 összefüggés adja meg, ahonnan az idő 6,35x107 s, azaz hozzávetőleg két évnek adódik. A számítás tarthatatlanságát azonnal látjuk, hiszen ekkor az űrhajó hamarabb érkezne meg, mint a fény, a végsebesség pedig v = g.t = 6,35x108 m/s lenne, ami több mint kétszerese lenne annak, amivel a fény halad!
A relativisztikus sebességváltozás
A relativisztikus hatást a hosszúság
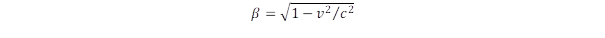
Lorentz kontrakciójával írhatjuk le, amiért a sebesség nem egyenletesen, hanem annál lassabban növekszik a
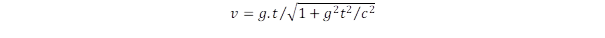
összefüggés szerint. A relativisztikus és nem-relativisztikus sebességváltozást mutatja az ábra:
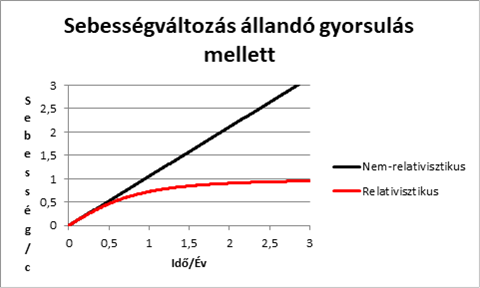
Az út számításához az idő szerinti integrálást elvégezve és kisebb átalakítás után kapjuk a megtett út és az idő közötti relativisztikus kapcsolatot:
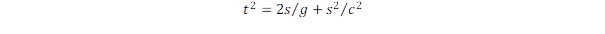
Itt az első tag megfelel a nem-relativisztikus járuléknak 2s/g = 4x1015 s2, míg a relativisztikus tag ennél kissé nagyobb: s2/c2 = 4,44x1015 s2. Az innen számított idő t = 9,19x107 s = 2,9 év. Tehát annyi idő kell az út első feléhez. A teljes utazás ideje ennél négyszer hosszabb, ha nem számítjuk az csillagrendszer felkutatására szánt időt, ami összességében 11,6 év lenne, ami elfogadható időtávnak tekinthető az expedíció életében.
A relativisztikus hatások mértéke
Nézzük meg, hogy az út felénél, amikor a Földhöz képest maximális a sebesség: v = 2,852x108 m/s (lásd a sebesség korábbi képletét) mekkorák a relativisztikus effektusok. Ez a fénysebességnek már a 95 százaléka és a hozzá tartozó Lorentz kontrakció: β = 0,31, ami azt jelenti, hogy a hosszúság ennek mértékében rövidül le és ennyiszer jár lassabban az óra és mintegy háromszor lesz nagyobb a tömeg. Az űrhajó utasai persze ezt nem érzik, számukra minden olyan, mintha a Földön lennének. De képzeljük el, hogy elhaladnak egy másik űrhajó mellett, amelynek sebessége azonos a földivel. Ebből az űrhajóból nézve látszik úgy, hogy a másik űrhajó méterrúdja csak 31 cm, az óra is lassabban jár: egy perc alatt úgy látják, hogy a másik helyen alig 20 másodperc telik el. Ha az egyik űrhajón eldobnak egy súlygolyót, az sokkal rövidebbre száll el, amit úgy értelmeznek, hogy odaát a súlygolyó mintegy háromszor nehezebb.
Mennyivel lesznek fiatalabbak az űrhajósok?
A relativitáselmélet egyik furcsaságát reprezentálja az ikerparadoxon. Ha összehasonlítjuk, hogy mennyi idő telik el az űrhajó utasa számára az otthonihoz képest, akkor megkapjuk, hogy a visszatéréskor mennyivel lesz fiatalabb. Itt a számításnál az idő dilatációjából induljunk ki:
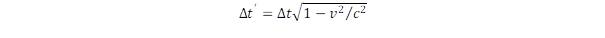
A sebesség növekedésével fokozódik az idő dilatáció. Ezt az első szakaszra integrálva kapjuk meg a teljes időt:
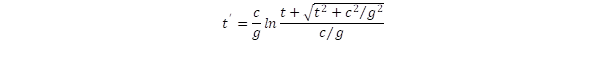
Az idő változását a Földön és az űrhajóban mutatja az ábra:
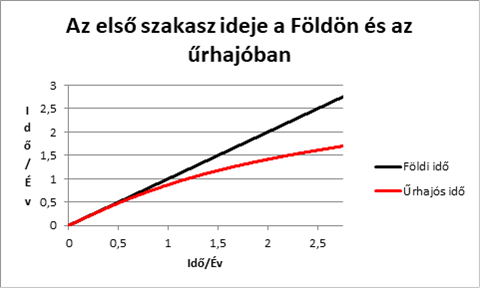
E szerint az űrhajósok által az indulástól mért idő t’ = 5,514x107 s = 1,75 év lesz. A négy szakasz együttvéve így 7 évet tesz ki, tehát hazatérve 11,6 év helyett, csak 7 évet öregszenek, a fiatalodásuk tehát 4,6 év lesz. Ez a hét év még annál is rövidebb 1,6 évvel, ami a fény számára kell, hogy oda-vissza megtegye az utat.
Folytatás a következő bejegyzésben
A csillagközi utazás számára tehát nem a szükséges idő a legfőbb akadály. Az igazi problémát a megfelelő „üzemanyag” és annak előállítása és robbanásveszélye lenne. Erre térek ki a blog következő bejegyzésében.
A korábbi bejegyzések összefoglalását és a megfelelő linkeket lásd: „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”.