A Hawking sugárzás

Az Univerzum már 13,7 milliárd éve fennáll és semmi jel nincs arra, hogy pusztulás fenyegetné. A fizikai törvényeit ezért úgy kell megfogalmazni, hogy módosítsuk az olyan elméleteket, amelyből mégis erre kellene következtetni. Ilyen javaslatot tett meg Stephen Hawking is a feketelyukakról, aki egy olyan tudós, akinek a megnyilvánulásaira mindig érdemes odafigyelni, mert ötleteivel már több alkalommal adott lökést alapvető kérdések megoldásához. Egyik vesszőparipája a feketelyukak sorsa. Ő vetette fel a ma már széles körben elfogadott elképzelést a feketelyukak sugárzásáról, ami megakadályozza, hogy túlnőjenek egy határon, sőt eltűnésükhöz is vezethet. Gondolata tengelyében az információ megmaradás elve van: valamiképp a feketelyuk által elnyelt objektumokban tárolt információnak fenn kell maradni, még ha átváltozott formában is.

Miért létezik az univerzum?

Én a feketelyukak problémáját más irányból indítom el. Mi következik az univerzum stabil létezéséből? Először is a kölcsönhatások véges sebessége. Mert mi történne, ha a kölcsönhatás késleltetés nélkül érkezne meg? Ekkor minden hatásra azonnal érkezne válasz, ami végtelen számú válasz egyidejű halmozódását idézné elő, és ez az univerzum felrobbanásához vezetne. Tehát van egy véges és állandó kölcsönhatási sebesség, ez pedig a fénysebesség, amely viszont Einstein megfogalmazásában a relativitáselmélet alapja. Lásd még: „Miért relativisztikusak a fizikai törvények”

A relativisztikus tömegnövekedés

Az elmélet egyik következménye, hogy a megfigyelőhöz képest a tömeg megnövekszik az

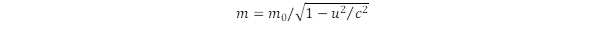
összefüggés szerint, és amiért az u sebesség sem érheti el c-t, hiszen ha az m₀ nyugalmi tömeg nullától különbözik a mozgási tömeg végtelen nagy lenne. Emiatt a fény csak nulla nyugalmi tömeggel rendelkezhet.

Van-e a fénynek tömege?

A relativitáselmélet másik alapvető megállapítása a tömeg és az energia ekvivalenciája E = m.c². De a fotonnak van energiája: E = h.ν,  (ν  a frekvencia), azaz mégis van tömege a fénynek! A foton tehát rendelkezik tömeggel, meg nem is? A látszólagos ellentmondás azonban feloldható, ha a matematika határérték fogalmára gondolunk. Ha egy X szám a végtelenhez tart, akkor 1/X végtelenül közel kerül a nullához, de a két mennyiség szorzata mégis egy marad, hiszen X.(1/X) = 1. A foton nyugalmi tömegét ezért nullához tartó határértéknek kell tekinteni, ahol X a végtelenhez közeledő tömegnövekedési arány és 1/X a nyugalmi tömeg. Más szóval a fénysebességű mozgás teremti meg a tömeget!  Ez az a gondolat, ami utat nyit, hogy megértsük, hogyan jön létre univerzumunk valamennyi részecskéjének tömege, és ezt fogalmaztam meg a fénysebességű forgások elvével.

A fény impulzusnyomatéka: a spin

Minden foton rendelkezik még egy különleges tulajdonsággal, van spinje, azaz saját impulzusnyomatéka, amelynek nagyságát a redukált Planck állandó adja meg: ℏ = h/2π. De mi kell ahhoz, hogy egy fizikai objektumhoz impulzusnyomatékot rendeljünk? Kell egy m tömeg és egy r forgási sugár. Azonosítsuk a foton ν  frekvenciáját a forgás frekvenciájával és legyen a forgás kerületi sebessége a c fénysebesség, azaz c = 2πν.r. Az r sugarú, c kerületi sebességű és m tömegű pontszerű objektum impulzusnyomatéka viszont  I = m.c.r = (h.ν/c²).c.(c/2πν) = h/2π lesz. Tehát, ha a fotonhoz fénysebességű forgást rendelünk, akkor tetszőleges frekvencia, azaz energia esetén a foton impulzusnyomatéka épp a redukált Planck állandó lesz. A foton fénysebességű forgásmodellje ily módon ellentmondásmentesen értelmezi a foton valamennyi fizikai paraméterét! Ezt a modellt kiterjeszthetjük valamennyi részecskére is, így a fermionokra, amelyek spinje ½. Ezek a nyugalmi tömeggel rendelkező részecskék nem mozoghatnak fénysebességgel, de két egymásba ágyazott fénysebességű forgásuknak köszönhetik tömegüket és ez magyarázza a spin feleződését és az elektromos töltés megjelenését is. Lásd a további bejegyzéseket: „Az elemi részecskék mozgásformái”, „A tömeg és töltés kettős arculata”, „Fénysebességű forgások és a relativitáselmélet”.

Milyen erő tartja fent a részecskék sajátforgását?

De válaszolnunk kell egy alapvető kérdésre, hogy milyen erő tartja fenn a részecskék sajátforgását? Erre szükség van, mert ha egy m tömegű test ω = 2πν frekvenciával forog, akkor azt az F  = m.ω²r centrifugális erő akarja kirepíteni! Kell tehát egy centripetális ellenerő, ami a forgást fenntartja. De honnan származik ez az erő? Annak érdekében, hogy a választ megadjuk, szükségünk van a gravitáció elméletére is, aminek alapjait Einstein fogalmazta meg az általános relativitáselméletben. 

A gravitációs elmélet dilemmája

Térjünk ki evvel kapcsolatban a modern fizika talán legnagyobb megoldatlan kérdésére, ami a gravitáció elméletéből fakad. A mai fizika négy alapvető erőt tart számon: a gravitáció és az elektromágneses erők mellett két további erő létezik, az egyik a részecskéket átalakító gyenge kölcsönhatás, a másik a részecskéket összeforrasztó erős kölcsönhatás. A modern fizika úgy képzeli el, hogy minden egyes kölcsönhatást virtuálisan kibocsátott és elnyelt bozonok hozzák létre. Itt a virtualitás azt jelenti, hogy ezek a részecskék közvetlenül nem detektálhatók, de jelenlétük rendkívüli pontossággal írja le a kölcsönhatásokat, a bozon pedig olyan részecske, amelynek egységnyi a spinje, azaz a saját impulzusnyomaték a redukált Planck állandóval egyezik meg. Az elektromágneses kölcsönhatás bozonja a foton, a gyenge kölcsönhatásé a tömeggel rendelkező W és Z bozonok, az erős kölcsönhatást pedig gluonokkal írják le az un. tér- (pontosabban mező-) elméletekben. Ennek mintájára tételezik fel a gravitáció bozonját is, amit gravitonnak neveztek el és spint is rendeltek hozzá. Ezek a mezőelméletek a kvantummechanikán alapszanak, egységes keretek között tárgyalják a kölcsönhatásokat, de nem alkalmazhatók a gravitáció leírására. Lásd még: „Barangolás a kvarkok és elemi részecskék világában”, „A kvark szine”, „Az elektro-gyenge kölcsönhatás és az elemi részecskék átalakulása”

A tér görbülete és a gravitáció

Annak okát, hogy a gravitáció miért nem kezelhető hasonló mezőelmélettel, mint a többi kölcsönhatás, megérthetjük a részecskék fénysebességű mozgását ellensúlyozó centripetális erő eredetének tisztázásával. Kiindulópontunk az általános relativitáselmélet alapelve, mely szerint a gravitáció forrása a nem-euklideszi tér görbülete. Minden körforgás a relativitáselmélet szerint görbületet hoz létre a térben. Ennek oka a Lorentz kontrakció, amely szerint a mozgás irányában a távolságok lerövidülnek:

,

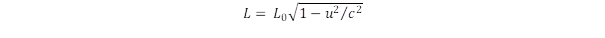
de ugyanakkor a mozgásra merőleges irányban nincs változás. Emiatt az r sugarú kör kerülete nem az euklideszi geometriában érvényes 2r.π lesz, hanem annál rövidebb. A görbület nulla az euklideszi geometriában, ezért úgy jellemezhetjük a körforgás okozta görbületet, ha a rövidülés négyzetét kivonjuk az egységből, azaz a

Görbület =  u²/c² = ω²r²/c²

Az összefüggés megmutatja, hogyan függ a görbület a frekvenciától és a sugártól.  A Görbület ennek értelmében nulla és egy között változhat, hiszen a kerületi sebesség nem haladhatja meg a fénysebességet. Ezt a görbületet kell kapcsolatba hozni a gravitációs erővel.

A Kepler törvény értelmezése virtuális forgásokkal

Először azt vizsgáljuk meg, hogyan értelmezhetjük ily módon a newtoni tömegvonzás törvényét, mely szerint a m és M tömeg közötti vonzó erő a két tömeggel arányos és a távolság négyzetével csökken: F_gr = G.m.M/r², ahol G az általános gravitációs állandó. Legyen M sokkal nagyobb, mint m, ez a Nap körül keringő bolygók esetén teljesül. A körmozgás m.ω²r centrifugális erejét a gravitációs erő egyenlíti ki, és ez az egyenlőség pedig vezet el a bolygómozgás Kepler törvényéhez:

ω²r³ = G.M

 Ez a törvény tetszőlegesen kis tömegű keringő objektumra is vonatkozik, ezért ha a tér pontjait úgy fogjuk fel mint határértékben nulla tömegű objektumokat, akkor maga a tér is végezhet a Kepler törvénynek megfelelő forgásokat. A tér pontjait azonban nem látjuk, ezért ez virtuális forgásnak felel meg. A virtuális forgások tengelye tetszőleges lehet, de amikor már egy véges nyugalmi tömegű objektum (például egy bolygó, hold, vagy egyéb objektum) végez körforgást a Nap körül, akkor ez már valamelyik virtuális pályát fogja kiválasztani. Ez a szemléletmód pontosan megfelel a kvantummechanikának, amikor a mérés előtt csak valószínűségi eloszlást adunk a pályára a hullámfüggvény segítségével, a mérés viszont már egy konkrét pályáról nyújt információt. Ezt nevezi a kvantummechanika a hullámfüggvény redukciójának.

Az erős gravitáció koncepciója

Hasonlítsuk össze a görbületre kapott korábbi kifejezést a Newton törvénnyel:

Görbület.c² = G.M/r

 Itt a jobboldali kifejezés az egységnyi tömegre ható potenciális energiának felel meg, ezért

V_gr = Görbület.m.c²

Mivel a fénysebességű forgás egységnyi görbületet hoz létre, így ehhez a forgáshoz éppen m.c² potenciális energia tartozik, azaz pontosan megegyezik az m tömegű objektum energiájával!

A részecskék két alaptípusánál, a bozonoknál és a fermionoknál, ez azt jelenti, hogy a fénysebességű forgás által létrehozott elemi objektumokban a térgörbület vonzó ereje, amit ERŐS GRAVITÁCIÓNAK lehet nevezni, épp kiegyenlíti a sajátforgások centrifugális erejét. Ahogy azt egyéb bejegyzésekben leírtam valamennyi kölcsönhatási bozon értelmezhető, mint egy fénysebességű forgás, (gluonoknál rezgés) és egy transzláció kombinációja, ezért a mezőelméletek alapelvét, mely szerint minden kölcsönhatás virtuális bozonokkal írható le, úgy is megfogalmazhatjuk, hogy minden kölcsönhatás virtuális forgásokhoz rendelhető. Ez a felfogás már lehetőséget teremt, hogy a gravitáció is hasonlóan értelmezhető legyen, mint a többi kölcsönhatás. A gravitáció annyiban különbözik a többitől, hogy ekkor a virtuális forgások kerületi sebessége nem egyenlő a fénysebességgel. Az egyesített mezőelmélet megteremtésének kudarca ezért arra vezethető vissza, hogy ezek a forgások nem rendelkeznek az alapvető részecske tulajdonsággal, mert csak a fénysebességű forgás hozhat létre tömeget és spint.

A Planck állandó eredete

Megadhatjuk az erős gravitáció potenciális energiájának távolságfüggését is:

V_sgr = m.c² = ℏ.ω = ℏ.c/r

Ebből képezhetjük az erős gravitáció centripetális erejét:

F_sgr = ℏ.c/r²

Ezáltal a Planck állandó eredetére is új értelmezést kapunk: ez az állandó a tér fénysebességű forgásához tartozó kölcsönhatási állandó.

A feketelyukak hígulása

A fentiek alapján már választ adhatunk a feketelyuk problémára is. Az Einstein féle gravitációs egyenletnek szinguláris megoldása van, mert nincs felső határ a tér görbületére és a végtelenhez tartó görbület már csapdába ejtheti a fényt bármekkora is legyen annak energiája. Az általam javasolt elképzelésben viszont a görbület nem lehet akármekkora, mert ez ellenkezik avval az elvvel, hogy a sebesség nem lehet nagyobb, mint a fényé. A Kepler törvény szerint a kerületi sebesség

u² = G.M/r

Mivel u nem lehet nagyobb c-nél, így az M tömegű objektum körül keringő objektum távolsága nem lehet kisebb, mint G.M/c². Ez vonatkozik minden részecskére [1] és a feketelyukakra is. Ez a kritikus sugár arányosan növekszik a tömeggel, de ugyanakkor az objektum  M/r³-al arányos sűrűsége csökkenni fog. Ez okozhatja, hogy a feketelyuk mérete sem lehet bármekkora és a feketelyuk „hígulása” egy határ után már nem tudja visszatartani a sugárzást és beindul a Hawking által javasolt mechanizmus.

A blog további bejegyzéseinek összefoglalóját lásd: „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”

1. Látszólag ennek ellentmond az elektron, amely bizonyos szórás kísérletekben pontszerűen viselkedik. Ennek oka a fénysebességű forgás modellben arra vezethető vissza, hogy az elektron felülete a Lorentz kontrakció miatt nulla lesz, viszont az r sugár továbbra is véges marad, ami a Compton hullámhosszal (h/m.c) egyezik meg.