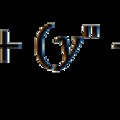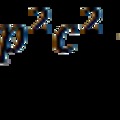A csillagközi utazás ideje
A bejegyzés első részében vettettem fel a kérdést, hogy milyen időtávon oldható meg egy látogatás a legközelebbi csillagrendszerbe, az Alfa Kentaurihoz („Csillagközi utazás az Alfa Centaurira”). Kiindulópontom az élettani szempont volt, hosszabb távon szervezetünk nem bírna el olyan terhelést, amely a földi gravitációt meghaladó gyorsulással járna együtt. Evvel a gyorsulással a relativitáselmélet szabályait figyelembe véve kiszámolható, hogy az oda-vissza úthoz 11,6 év kellene, az űrhajósok korosodása azonban ennél rövidebb, úgy 7 év lenne, ami vállalható hosszúság az expedíció számára. Az igazi probléma azonban, hogy ehhez az úthoz mennyi üzemanyag kell, és milyen veszélyekkel járna az egész emberiségre nézve is, nem beszélve az űrhajósokról.
Mennyi üzemanyag kell a csillagközi úthoz?
Becsüljük meg, hogy mennyi üzemanyagot kell az m tömegű űrhajónak magával vinni, hogy biztosítsa az m.g.s gyorsítási munkát. ahol g = 10m/s2 a gyorsulás és s = 8x1016m (2x4,3 fényév) a teljes út hossza a csillagig és vissza. Az M üzemanyagból nyerhető maximális energia M.c2, ennél csak kisebb lehet a ténylegesen kinyert energia, aminek hatásfokát jellemezzük η-val: ηMc2. Az üzemanyag tömege ezért jóval nagyobb lesz, mint a hasznos tömeg, hiszen:
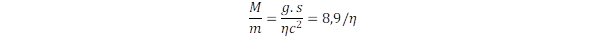
Az üzemanyag hatékonyság szerepe az űrutazásban
Ha bármilyen kémiai üzemanyagot használunk a hatásfok kisebb, mint egymilliárd, nukleáris bomláskor felszabaduló energiát használva sem érhetünk el egy tízezrednél nagyobb hatásfokot, még fúziós reakciókat felhasználva sem remélhetünk többet 1 százaléknál. Még ebben az esetben is legalább ezerszer nagyobb lesz az üzemanyag tömege az űrhajó saját tömegéhez képest. A helyzet azonban ennél sokkal rosszabb, hiszen végig kell biztosítani az üzemanyagot, ezért magát az üzemanyagot is fel kell gyorsítani, még ha útközben fokozatosan csökkenni fog ennek mennyisége. Az állandó gyorsulás miatt a mindenkori fogyás arányos lesz a tömeggel, ezt a

differenciálegyenlet írja le, ami az
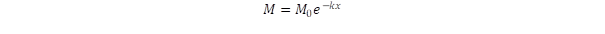
exponenciális fogyási törvényhez vezet. Itt a k arányossági együttható adja meg, hogy egységnyi megtett út során az üzemanyag hanyadrészét kell felhasználni. Ezt megkapjuk, ha az egységnyi úthossz alatt végzett M.g munkát összevetjük a felhasznált ηkMc2 energiával:
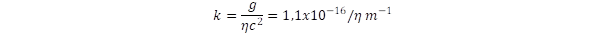
Hogyan viszonyul az üzemanyag mennyisége a hasznos tömeghez?
A teljes út megtétele után az exponenciálisan csökkenő tömeg értéke:
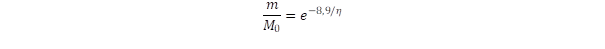
Ez pedig azt jelenti, ha sikerülne 100%-ban hasznosítani az üzemanyag nyugalmi energiáját, akkor is az üzemanyag tömege 7250-szer nagyobb lenne, mint az űrhajóé. Egy ilyen expedíciónak 100 tonnánál kisebb tömegű űrhajónál kisebbel aligha lehetne nekivágni, ezért az induló tömeg legalább egymillió tonna lenne, ami már egy közepes hegy tömege. Ha azonban fúziós folyamatokkal elérhető hatásfokot vennénk alapul, akár az egész Nap tömege is nagyon kevés lenne az úthoz.
A leghatékonyabb energiatermelés antirészecske reaktorral
Tehát az expedícióhoz alapkövetelmény lenne az egységnyi hatásfokú energiafelhasználás. Lehetséges-ez? Elvben igen, ha az anyag-antianyag annihiláció lenne az energiaforrás, mindenek előtt az antiproton és a protonok annihilációja lehetne az alap. A probléma természetesen az antiprotonok összegyűjtése és tárolása lenne, mert olyan tartályra lenne szükség, ahol az antirészecske nem érintkezhetne a tartály anyagával. Az antiproton töltött részecske, ezért mágneses térben körpályára kényszeríthető, emellett ha negatív töltésű lenne a tartály, akkor ez eltaszíthatná magától az antiprotonokat. Tehát elvben létrehozható ilyen elektromágneses csapda, de persze ehhez is energia kell, ami a működést biztosítja.
Az antirészecske reaktor kockázatai
Az antiprotonokat a kozmikus sugárzásból lehetne nyerni, mert annak energiája elég, hogy létrejöjjenek ezek a részecskék, de ha ezek a részecskék nagy tömegben vannak összegyűjtve, akkor a kockázat óriásira nő. Akkora mennyiség kellene, ami sokszorosan meghaladja a földön jelenleg tárolt hidrogénbombák teljes tömegét és egy esetleges robbanás hatásfoka ennek több mint százszorosa lenne. Elég egy apró technikai hiba és ha létrejön a robbanás az nem csak a földi életet pusztítaná el, hanem szétrobbantaná a föld kérgét is. Még nagyobb veszély fenyegetné az űrhajósokat, mert a fénysebesség közelében már nem lehetne előre látni, ha valamilyen nagyobb űrobjektum kerülne a pálya közelébe, és a manőverezés is nehéz ekkora sebességnél. Így aligha lehetne olyan biztonsági rendszert kifejleszteni, amely elegendő mértékben csökkentené az ütközés és emiatt a robbanás kockázatát.
A csillagközi űrutazás esélyei
Az elmondottak miatt bármilyen magas szintre emelkedjen a technika nincs értelme egy csillagközi expedíciónak, túl nagy lenne ennek kockázata. Járható út lehet azonban az automatikus űreszközök, dronok küldése, amelyeket földről irányított energiaforrások (lézerek) segítségével fel lehet annyira gyorsítani, hogy reális idő alatt elérjék a szomszédos csillagokat és onnan küldjenek számunkra híradást a szomszédos csillagok világáról. Folytonos gyorsulású űrhajók esetén erre nincs lehetőség, mert fényévnyi távolságra aligha küldhető már kellően fókuszált sugárzási energia. A csillagközi utazás ezért mindörökre megmarad a fikciók világában.
A korábbi bejegyzések összefoglalását és a megfelelő linkeket lásd: „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”.