A kvantummechanikai alagúteffektus ma már a mindennapi technika részévé vált az alagútdiódák kifejlesztésével, szintén fontos a szerkezetvizsgálatban is a szkenning alagútmikroszkópia területén, sőt ezen keresztül egy új tudományág, a kvantumbiológia kialakulásának is a tanúi vagyunk, de mi ennek a titokzatos jelenségnek az alapja? Ennek megértéséhez szükség van a mikrovilág törvényeinek megismerésére, amely sokban különbözik a klasszikus mechanika megszokott szabályaitól. Induljunk ki először egy klasszikus példából, például, hogyan tudja egy magasugró átugrani a magasra tett lécet?

A magasugró példája

Az a sebesség, amivel egy jó ugró felpattan a rekortánról 5 m/s körül van. Milyen magasra emelkedhet? A felfelé történő mozgás kinetikus energiája ½mv² alakul át az m·g·h potenciális energiává, amikor eléri a maximális magasságot, ezért h =  ½v²/g = 127 cm az elérhető emelkedés, figyelembe véve a test súlypontjának magasságát, ami az ugró testalkatától függ ez megtoldható 80- 100 centiméterrel, de ezzel még csak maximum 227 cm-nél tartunk, aminél a magasugrás világcsúcsa jóval nagyobb (245 cm, Sotomayor, 1993). Ennek oka, hogy megfelelő ugrástechnikával (Fosbury flop) a súlypont alatta maradhat a léc magasságának, mert az ugrás közben a test forgást végez, és amikor a léc fölé ér, a hát meghajlításával a  kéz, a fej és a lábak megfelelő pozíciójával a súlypont alacsonyabbra kerül. Természetesen az elektron nem tud hasonló eszközökkel élni, viszont segíti a kvantummechanika alagúteffektusa.

Kvantummechanikai alapfogalmak

Az alagúteffektus megértéséhez elengedhetetlen a kvantummechanika néhány alapelvének megfogalmazása. Ezt részletezi az „Út a kvantummechanika megértéséhez” című bejegyzés, amelynek itt csak néhány alapelemét ismertetem. Ami a legfontosabb, hogy értsük a klasszikus fizikai és a kvantumelven alapuló gondolkozás különbségét. Amikor mozgásokat írunk le, három alapkérdésre kell válaszolni: mi az ami állandó marad, mi az ami megváltozik és végül, hogy mi hozza létre a változást.

Az energia operátor és az állapotfüggvény

Minden mozgás, minden fizikai átalakulás legfőbb állandója az energia. Ez voltaképp az energia definíciója. Ha valami időben nem változik, arra a fizika azt mondja, hogy a vizsgált rendszer állapota állandó marad. A kvantummechanika alapelve, hogy a fizikai mennyiségeket hatásuk alapján definiálja, ennek megfelelően az energia operátora az a hatás, amely nem változtatja meg időben a fizikai objektum állapotát. Az idő szerinti változtatás matematika megfelelője a δ/δt differenciálhányados, ezt alkalmazzuk valamilyen δ(t) függvényre, amit a vizsgált fizikai objektum állapot meghatározójának tekintünk. Az állapotfüggvény változatlanságán azt értjük, ha képezzük ennek differenciálhányadosát, akkor egy konstans szorzótól eltekintve változatlan alakban kapjuk vissza az eredeti függvényt. Ez a konstans szorzó, amit az operátor sajátértékének nevezünk, határozza meg a klasszikus értelemben vett energiát. Szorozzuk még meg az idő szerinti differenciálhányadost a redukált Planck állandóval és az imaginárius egységgel, hogy eljussunk az energia operátorához (ennek indoklását a fent említett bejegyzés tárgyalja):

 Schrödinger egyenlet

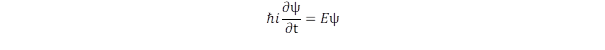
A mechanikai energiát két tag összege adja meg akár a klasszikus, akár a kvantummechanikáról van szó, mégpedig a kinetikus és a potenciális energia: E = E_kin + V. Nem-relativisztikus közelítésben a kinetikus energia:

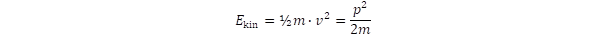
A p = m·v impulzus a mozgás másik fontos „megmaradási” mennyisége, amely a Noether-elv szerint azt fejezi ki, hogy a térkoordináták kezdőpontjának megválasztásától nem függ az impulzus értéke. Fogalmazhatunk úgy is, hogy az impulzus hatása a térbeli eltolással szembeni változatlanságban mutatkozik meg. Válasszuk meg a mozgás irányában az x tengelyt, ekkor a részecske mozgási állapotát jellemző ψ(x) állapotfüggvény x szerinti deriváltja, azaz δ/δx írja le az impulzus hatását. A megfelelő fizikai dimenzióhoz úgy jutunk el, ha a deriváltat szorozzuk a ℏ/i együtthatóval, mely szerint az impulzus operátora: ℏ/i ·δ/δx. Ezt behelyettesítve a kinetikus energiában p helyébe jutunk el az egydimenziós Schrödinger egyenlethez:

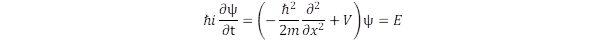
Stacionárius állapot

Ha a potenciális energia csak x-től függ és időben változatlan, akkor az egyenletből származtathatjuk az időtől független E energiát, ezt nevezzük stacionárius megoldásnak, amelyhez olyan állapotfüggvény tartozik, amelyben az idő és térkoordinátától függő rész szétválik:

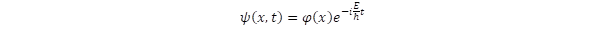
A mozgást leíró klasszikus pálya abban tér el a kvantummechanikai állapotfüggvénytől, hogy az előbbiben nem választható szét a térbeli és időbeli függés, amit a sebességgel és a gyorsulással adunk meg. Stacionárius állapotban viszont nem beszélünk sebességről és gyorsulásról, pontosabban azt mondjuk, hogy kötött állapotban ezek várható értéke nulla. A várható érték egy statisztikai jellemző, amely megmondja, hogy átlagban mekkora az egyes fizikai mennyiségek értéke és az átlagot a Ψ(x,t) függvénnyel képzett integrál adja meg.

A hullámfüggvény rejtett fázisa

Minden kvantummechanikai számításnál, legyen szó a részecske térbeli tartózkodásának valószínűségéről, az egyes fizikai mennyiségek várható értékéről, vagy két stacionárius állapot közötti bekövetkező átmenet valószínűségéről, fellép az állapotfüggvény és ennek komplex konjugáltjának szorzata. Ennek a szorzatnak a teljes térre számított integrálját választjuk egységnek, ami a részecske identitásának kritériuma, amivel azt fejezzük ki, hogy mindig a teljes részecskét definiáljuk a térben és nem annak törtrészeit. Ez a matematikai eljárás a hullámfüggvény normálása.

A szorzat alakban felírt állapotfüggvény (lásd a 4. egyenletet) második tényezője az időbeli változás exponenciális függvénye, amely olyan periodikus változást ír le, ahol az amplitúdó egységnyi:

Itt a periodikus változás körfrekvenciáját az energia határozza meg: ω = E/ℏ. A kvantummechanikai részecske, például az elektron az atomban és molekulákban, eszerint „láthatatlan” körforgást végez, amit az időben változó ω·t fázis jellemez. Ez a fázis azonban rejtett marad, mert az exponenciális függvény szorzata komplex konjugáltjával egyet ad ki, vagyis nem módosítja sem az egyes operátorok sajátértékét, sem az átmeneti valószínűséget, más szóval ez a fázis nem mutatkozik meg méréseink eredményében. A fizikai mennyiségeket kizárólag az állapotfüggvény φ(x) tényezője határozza meg, amely viszont valószínűségi jelleget ad méréseinknek, ennek jól ismert folyománya a Heisenberg féle bizonytalansági reláció. Összefoglalóan úgy is fogalmazhatunk, hogy a stacionárius állapotban történő mozgás nem a tér és idő, hanem a tér és valószínűség dimenzióiban megy végbe.

EPR paradoxon

Bár az időben periodikusan változó fázisnak nincs közvetlen szerepe méréseink kiértékelésében, még is fontosak, ha érteni akarjuk a kvantummechanikai folyamatok statisztikus jellegét és az interferencia jelenségét. Amikor az elektromágneses sugarak elektronokra gyakorolt hatását vizsgáljuk, csak annak valószínűséget tudjuk megmondani, hogy mi lesz a kölcsönhatás eredménye, de mi történik, ha egy konkrétan kiválasztott elektronról, vagy fotonról van szó, akkor mi dönti el a folyamat eredményét? Ilyen és hasonló kérdéseket tárgyal az EPR (Einstein-Podolsky-Rosen) paradoxon. A paradoxon feloldását épp a rejtett fázis segítségével találhatjuk meg (lásd: EPR paradoxon).

Az alagúteffektus potenciálfüggvénye

A kvantummechanikai mozgások jellegének ismeretében már felkészültek vagyunk, hogy megértsük az alagúteffektust is. Kövessük a legtöbb tankönyvben ismertetett utat. Először építsük fel azt a potenciálteret, amiben tanulmányozhatjuk a jelenséget. Egydimenziós közelítést alkalmazunk, amelyben az x koordináta mentén különböztetünk meg szakaszokat. Az első szakasz a negatív x értékekre korlátozódik, ahol a potenciális energia megadása nélkül csak annyit tételezünk fel, hogy a részecske valamilyen E energiájú stacionárius állapotban van. A második szakasz x = 0-tól x = d-ig tart, ahol fellép a V₀ potenciálgát, majd a harmadik szakaszban, ahol x nagyobb d-nél ismét legyen V = 0. Stacionárius állapotról van szó, ezért mindhárom szakaszban az energia E lesz. A Schrödinger egyenlet az időtől való függés leválasztása miatt csak a φ(x) függvényre szorítkozik:

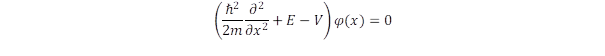
A hullámfüggvényt kielégíti az

exponenciális függvény, ahol a k hullámszámot meghatározó összefüggés:

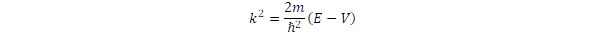
Az exponenciális függvény egydimenziós hullámot ír le. Az első és harmadik szakaszban V = 0, ezért a két esetben megegyezik a k hullámszám. A gáthoz érkező hullám részben visszaverődik, ezt úgy vesszük figyelembe, hogy egy A’ amplitúdójú és negatív exponensű tagot is felírunk. A harmadik szakaszban csak továbbhaladó hullámmal számolunk, amelynek amplitúdóját C-vel jelöljük. A második szakaszban viszont olyan a potenciálgát, amely magasabb az E energiánál, amiért negatív számból kell elvégezni a négyzetgyökvonást a (8) definíciós egyenletben, és így a gátba behatoló hullám elveszti periodikus jellegét és exponenciális növekedésnek, illetve csökkenésnek felel meg, amit a

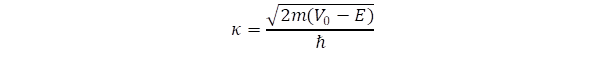
kitevővel és B illetve B’ amplitúdókkal jellemzünk:

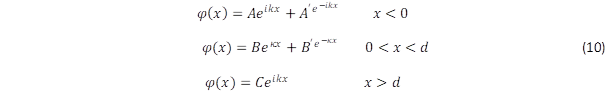
Az állapotfüggvény illesztése

Az alagúteffektus átviteli tényezőjét az A bemenő és a C továbbhaladó hullám amplitúdó négyzetének aránya fejezi ki, amit megkaphatunk a hullámfüggvény szakaszhatárokon való illesztésével. Az illesztés a függvények folytonos áthaladásán kívül megköveteli a deriváltak folytonos áthaladását is, mert csak így értelmezhető a hullámegyenletben szereplő második derivált. Ez négy független összefüggést jelent, amely elegendő az C²/A² arány meghatározásához:

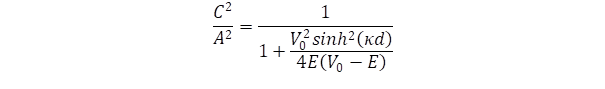
A transzmisszió függése a gátmagasságtól és szélességtől

A transzmissziós valószínűség egyaránt függ a potenciálgát magasságától és szélességétől. Ezt mutatja be az ábra az E = 1 eV = 1,6·10^-19 J energiájú elektron esetében.

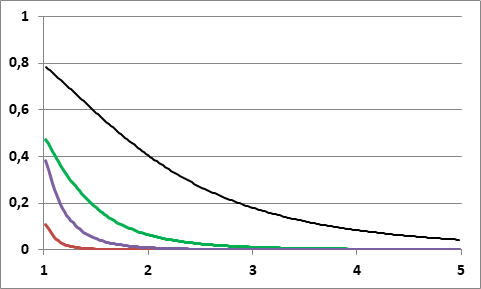
A vízszintes tengelyen a V₀ potenciálgát magassága szerepel 1 és 5 eV között, a fekete vonal felel meg 0,2 nm, a zöld 0,4 nm, a lila 0,6 nm és a piros 1 nm szélességű potenciálgátnak, demonstrálva a körülményeket, amikor a vezetőben egy, kettő, három, vagy öt molekuláris szigetelő rétegen kell az elektronnak átugrani. A függőleges tengely mutatja a transzmissziós valószínűséget, ahol az egység felel meg annak az esetnek, amikor minden elektron áthalad a potenciálgáton.

Látható, ha csak egyetlen szigetelő réteg van, akkor még jelentős magasságú gáton is áthaladhat az 1 eV energiájú elektron.

A számítások szemiklasszikus jellege

Bár a fent bemutatott számítások megfelelő leírást adnak a kísérletileg megfigyelhető alagúteffektusra, a belőle levonható elvi megállapításokat óvatosan kell fogadni, mert az eljárás nem követi a kvantummechanika szigorú szabályait, hanem ötvözi azt a klasszikus fizika elemeivel. Helyesebb ezért a módszert szemiklasszikusnak nevezni, ahogy ez Geszti Tamás könyvében is szerepel („Kvantummechanika”, Typotex, 2014, 67. oldal). Sajnos vannak olyan tankönyvek is (G. Heber – G. Weber, „A modern kvantumfizika alapjai”, Műszaki Könyvkiadó, 1964, 97. oldal), ahol úgy illusztrálják a klasszikus és kvantummechanika különbségét, hogy nem tesznek említést a számítás szemiklasszikus jellegéről, már pedig megtévesztő két módszer különbségéről úgy beszélni, hogy közben a módszerek kombinációját alkalmazzuk.

Vegyük hát sorra, hogy milyen kvantummechanikával ellentétes lépéseket tettünk az előzőekben.

1. A kvantummechanikai függvények megkövetelik a normálhatóságot, mert ez fejezi ki, hogy egy egész részecskét írunk le. A bevezetett hullámfüggvények azonban nem normálhatók.
2. Stacionárius állapotban nem beszélhetünk arról, hogy a részecske valamilyen potenciálgáton áthalad, mert nem tartozik az ilyen állapothoz időfüggés, csak valószínűségi eloszlás. Időbeli folyamatot a kvantummechanika két stacionárius állapot közötti átmenetként tud kezelni.
3. Nem lehet a hullámegyenletet külön szakaszokban megoldani és utólag a hullámfüggvényt összeilleszteni, mert a kölcsönhatásban a teljes térre kiterjedő elektroneloszlás egyidejűleg vesz részt. Ez felel meg annak, hogy az elektron a teljes potenciálteret „letapogatja”, és nem csak a potenciálgátat érzékeli.

Alagúteffektus az alfa-sugárzásban

Térjünk most vissza a magasugró példájához. A mozgás egymás utáni szakaszokra bontható térben és időben, először jön a nekifutás, majd az elrugaszkodás és végül az ugró átlibben a léc felett. Itt az elrugaszkodás pillanatában kell összegyűjteni azt a mozgási energiát, ami elég lesz a potenciálgát leküzdéséhez. Vessük ezt össze egy kvantummechanika példával, az alfa-bomlással, amit az alagúteffektussal lehet magyarázni. Ennek megfigyelése az atomfizika hőskorában történt Henry Becquerel (1896) és a Curie házaspár (Marie és Pierre) által. Az alfa-sugárzás során Hélium atommagok távoznak a radioaktív elemből, míg a béta-sugárzásban elektronok, a gammában nagy energiájú elektromágneses sugarak lépnek ki. A radioaktív elemet száz körüli proton és neutron építi fel. A magot összetartja a nukleonok közötti erős kölcsönhatás, amit gyengít a protonok egymást taszító hatása. A nukleonok mozgása héjakba rendeződik, a legstabilabb héjban, ezt nevezik s héjnak, két proton és két neutron helyezkedik el. A héjakban történő mozgáshoz kinetikus energia tartozik, ami azonban nem elég a magból való kilépéshez. Mégis időről időre egy-egy alfa részecske kiszabadul, ezt lehet magyarázni az alagúteffektussal.

Az alagúteffektus következetes kvantummechanikai számítása

 Ennek következetes kvantummechanika számítása úgy történik, hogy számba vesszük a teljes potenciális energiát és meghatározzuk a soknukleonos rendszer lehetséges energianívóit és a hozzátartozó hullámfüggvényeket. Lesz olyan megoldás, amelyben az alfa-részecskét felépítő nukleonok tartózkodási valószínűsége a potenciálfüggvény belső tartományába esik, de mindig van egy kis valószínűsége annak is, hogy a nukleonok a külső tartományban vannak. Ezek a kötött állapotok. A klasszikus példával szemben, tehát a nukleonok „kívül” is vannak, meg „belül” is egy időben. De olyan megoldást is kapunk, ahol már kikerülnek a nukleonok a belső tartományból. A kvantummechanika játékszabályai szerint képezhetjük a két állapot közötti átmeneti valószínűséget, amelyben kulcsszerepet játszik a kötött állapot hullámfüggvényének külső tartománya. Az ilyen számítás természetesen rendkívül összetett és számos numerikus közelítő eljárást igényel. Emiatt szokás a fentiekben ismertetett szemiklasszikus, vagy úgynevezett szemiempirikus módszerekhez folyamodni, de ilyenkor tisztában kell lenni avval, hogy számításaink csak közelítő érvényűek. 

Csillagok fúziós reakcióinak alagúteffektusa

Az alagúteffektusnak köszönhetjük, hogy a csillagok és közötte Napunk is évmilliárdokig ontják magukból a fényt és a hőenergiát. A csillagok „üzemanyaga” a két nukleon: a proton és a neutron. Ha ebből kettőt-kettőt összeházasítunk, akkor a Hélium mag képződésével óriásai energia szabadul fel: ez a fúziós reakció. Van azonban egy óriási akadály: a protonok közötti elektromos taszító erő, amely olyan potenciálgátat alkot, amelyet először át kell lépni ahhoz, hogy a nukleonok elég közel kerüljenek egymáshoz, amikor is a nukleáris vonzóerők működésbe léphetnek. A potenciálgát átlépéséhez még az a hőmérséklet sem elég, ami a csillagok belsejében uralkodik (14 millió Kelvin), ezért szükség van egy közvetítő láncolatra, amelyben a Hélium mag több lépésben épül fel. Ennek két alaptípusát tételezik fel, amíg a Napban és a hozzámérhető méretű csillagokban a felépülés három lépcsőben történik deutériumon és ³He izotópon át, addig a nagyobb tömegű csillagokban egy hatelemű ciklus jön létre, amelyben részt vesznek a szén, a nitrogén és az oxigén izotópjai, ahol már az alagúteffektus elegendő hatásfokú az egyes reakciólépések fenntartásához. Ez vezet egy jól kontrollált folyamathoz megakadályozva a csillagok felrobbanását szupernóvaként.

Alagúteffektus fémes, fél- és szupravezetőkben

Az alagúteffektus magyarázza, hogy miért tudjuk felgyújtani a lámpát szobánkban. A fémes vezető felülete oxidálódik, ami szigetelőréteget hoz létre a kapcsolóban. Ezt azonban az elektronok átugorhatják az ismertetett okokból. Szupravezetőkben is fellép hasonló effektus, ami különösen jellemző a magas hőmérsékletű szupravezető kerámiákban. Ez a Josephson effektus, amelyet felhasznál a korszerű méréstechnika is. A legismertebb alkalmazás a félvezetőket illeti, amikor az alagúteffektus segítségével alakíthatunk ki olyan vezetési mechanizmust, amelyben az áram csak egy irányban folyhat, ezek az alagútdiódák. Ennek változata, amikor a dióda rezonanciaszerűen működik, mert a diszkrét kvantumnívók közötti átmenet valamilyen kritikus feszültség esetén jön létre.

A fémfelület egyes atomjainak megfigyelését teszi lehetővé a szkening alagútmikroszkóp (STM, scanning tunneling microscope). A működés alapja, hogy az alagúthatás kritikusan függ két fémes vezető anyag közötti távolságtól (az egyik a mérőtű, a másik a vizsgált fémfelület), a mérés pontossága eléri a tipikus atomméret egy százalékát (0,001 nm).

Kvantumbiológia

Az alagúteffektus fontosságát felismerte a biológia is, ami egy új tudományág a kvantumbiológia kifejlődéséhez vezetett. Ez a hatás szerepet játszik a fotoszintézisben, sejtek lélegzésében és különböző enzimatikus folyamatokban, így a DNA spontán mutációjában is. Az utóbbi reakció a protonok alagúteffektusán alapul a hidrogénhidak átrendeződése során.

A blog további írásainak összegzése a megfelelő linkekkel megtalálható a „Paradigmaváltás a fizikában” című bejegyzésben.