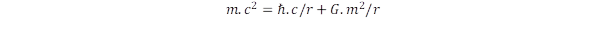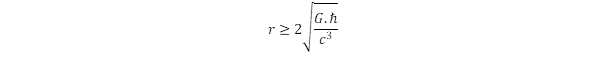A kvantum fogalmának kialakulása és térhódítása

Amikor Planck 1900-ban a fényt fotonokra, azaz kvantumokra bontotta a fekete test hősugárzásának értelmezése kedvéért, forradalmat indított el a fizikában. Ezt követte az atomok által kibocsátott diszkrét energiájú sugárzás értelmezése kvantumugrásokkal. A mikrovilág jelenségeinek matematikai leírására is megszületett a megfelelő eszköz, amelyben az egyes fizikai mennyiségeket hatásuk alapján határozták meg operátorok bevezetésével, az új eljárás a kvantummechanika nevet kapta. Az eredeti nem-relativisztikus Schrödinger és Heisenberg formalizmust Dirac fejlesztette tovább, amikor az energia relativisztikus egyenletét írta át operátorokkal. A módszer továbbfejlesztése a kvantumelektrodinamika, amit második kvantálásnak is neveznek, amelyben a fotonok és elektronok egyenrangú szerepet kapnak, mint a kvantumvilág elemei. Az elméletben valódi és virtuális fotonok szerepelnek, amit bozonoknak neveznek  S = 1 spinjük miatt, és ezek közvetítik az elektromosan töltött objektumok, úgymint az S = ½ spinű fermionok (például elektronok és protonok) közötti elektromágneses kölcsönhatást.

Ezek után a legtermészetesebb volt, hogy az elemi objektumok közötti minden egyéb kölcsönhatás esetén is kvantum természetet tételeztek fel. Az elképzelés sikeresnek bizonyult a részecskék átalakulását előmozdító gyenge kölcsönhatás értelmezésében, amikor is a foton mellett újabb S = 1 spinű bozonok jelentek meg, amelyek azonban tömeggel, sőt akár töltéssel is rendelkeztek. Sikerült végül az elektromágneses és gyenge kölcsönhatás elméletét egyesíteni, ami az elektro-gyenge kölcsönhatás nevet kapta. A következő lépés az atommagot alkotó protonok és neutronok, valamint egyéb rövid élettartamú részecskék (barionok és mezonok, összefoglaló néven hadronok) még elemibb alkotóit, a kvarkokat összetapasztó erős kölcsönhatás kvantumos értelmezése volt. Ebben nyolc  gluonnak nevezett részecske közvetíti a kölcsönhatást, ez az elmélet a kvantumkromodinamika nevet kapta. A sikerek meghozták a fizikusok étvágyát és fölvetették annak lehetőségét, hogy az elektro-gyenge és az erős kölcsönhatást is egyesíthető, aminek már előre nevet is adtak, ez a Nagy Egyesített Elmélet (GUT azaz Grand Unified Theory).

A kvantumelv túlburjánzása és a szuperhúr elméletek

Hátra volt azonban még egy kölcsönhatás, a gravitáció, amelyik sehogy sem akart beilleszkedni a képbe. Pedig a nagy álom az összes kölcsönhatás egyesítése volt, amire rögtön nevet is faragtak és nem kis nagyképűséggel a Mindenség Elméletének (ToE: Theory of Everything) neveztek el. Ez a törekvés már a kvantum fogalom mindenhatóságába vetett hitet tükrözi, ami mára már dogmává merevedett.

Az átfogó fizikai elmélet, a Nagy Egyenlet megalkotása volt Einstein álma is, aki ezen dolgozott élete utolsó harminc évében, de törekvése teljes kudarcot vallott. Einstein az általános relativitáselméletben sikeresen értelmezte a gravitációt, mint a teret torzító tömegek hatását, de ezt nem tudta összekapcsolni az elektromágnesességgel. Hasonló törekvések vezették az utána következő tudósgenerációt is, akik a részecske fogalmát próbálják rezgő húrokkal értelmezni, de mivel a szokásos háromdimenziós térben ilyet nem lehet megfigyelni, feltételezik egy negyedik térdimenzió létezését, ami az idővel együtt ötdimenziós téridőt alkot. A húrelmélet ötdimenziós változatáról hamar kiderült, hogy matematikai ellentmondásokra vezet, ezért nekiláttak újabb és újabb extra dimenziók hozzáillesztéséhez, így születtek meg további elméletek, amit szuperhúr, majd membrán, majd M-elméletnek neveztek el, sőt azóta már több új elnevezés is született. Ezekben az elméletekben már ott tartanak, hogy a bozonok 26, a fermionok 12 dimenzióban léteznek. Azt is kiszámították, hogy ezek a dimenziók olyan parányiak, amelyekhez képest még az atommagok is olyan hatalmasak, mintha egy gombos tű fejét hasonlítanánk a Nap méretéhez. Evvel annyit értek el, hogy magyarázhatták, miért lehetetlen ezeknek az új extradimenzióknak a megfigyelése. Ráadásul a dimenziók számának inflációja abban sem segített, hogy kiküszöböljék az elmélet ellentmondásait. Az elmélet további kiterjesztése a szuperszimmetria fogalmának felvetése (SUSY), amelyben minden bozonhoz egy fermion partnert és minden fermionhoz egy bozon partnert rendelnek, mint szimmetria kiegészítőt, viszont ezek tömege olyan nagy lenne, amely akár egy csillag tömegével is vetélkedhetne és ezért megfigyelésük jelenlegi műszereinkkel lehetetlennek tűnik.

Az Ősrobbanás és az univerzumok végtelen sokasága

Az elemi részecskék elméleteit előszeretettek kapcsolják össze az Ősrobbanás koncepciójával, aminek oka, hogy az elképzelt forró ősállapotban a részecskék olyan kölcsönhatásai is szerepet játszanak, amelyek az univerzum jelenlegi „konszolidált” viszonyai között nem figyelhetők meg. Az egyik kedvenc elképzelés, ami a fizikusok kimeríthetetlen fantáziáját mutatja, hogy párhuzamos univerzumok végtelen sokasága létezik, amiből létre jön a ma létező világ átvéve a többi univerzum energiáját. Ezek a „tudományos” elképzelések komoly szaklapokban kerülnek publikálásra, feltéve, hogyha a publikációt nagyra értékelt egyetem munkatársai írják. A tudományirányításban, a magas presztízsű pozíciók megszerzésében és a finanszírozási lehetőségek elnyerésében domináns szerepet játszanak azok az egyetemek és kutatási intézmények, ahol az ilyen és hasonló elméleti modelleket dolgozzák ki, ami oda vezetett, hogy a tényleges ismereteket feltáró alapfizika egyre inkább háttérbe szorul a technikai jellegű fejlesztéseket szolgáló kutatásokhoz képest. A szociológiai jelenség plasztikus leírását olvashatjuk Lee Smolin könyvében : „Mi a gubanc a fizikával”.

Valóban felfedezték a Higgs bozont?

Szóljunk néhány szót a Higgs bozon körüli felhajtásról, amit a zsurnaliszták előszeretettel neveznek isteni részecskének. Ennek alapja, hogy ezt a részecskét tekintik valamennyi megfigyelhető elemi fizikai objektum „megteremtőjének”. Higgs eredeti elképzelése absztrakt matematikai modellen alapul, amelyben a vákuumot metastabil állapotnak képzeli el. Ezt szokás a mexikói kalaphoz hasonlítani, ahol a kalap gömbszerű tetejére egy golyót helyeznek el, ami metastabil állapotot képvisel, mert bármely irányban legurulhat a golyó. A kiindulás tehát egy szimmetrikus állapot, ahonnan spontán módon, valamelyik irányt kiválasztva gurulhat le a golyó, ami által „megtörik” a szimmetria. Egy ilyen spontán szimmetriatörési folyamat, amikor a kezdő állapotból – ehhez rendelhető a Higgs bozon – létrejönnek az energia átadásával az egyes elemi részecskék. Az elmélet nem mondja meg, hogy mekkora a részecske energiája, viszont rögzíti, hogy mekkora a spin és az elektromos töltés. Az LHC (Large Hadron Collider) munkatársai nagy csinnadrattával jelentették be, hogy találtak egy nagy energiájú részecskét, ami szerintük alátámasztja Higgs hipotézisét. Erre erősített rá a Nobel Bizottság, amikor a felfedezést Nobel díjjal jutalmazta. Pedig az egész eljárás nem több mint „parasztvakítás”, hiszen az új részecskének csak a tömegét lehet tudni, szemben az elmélettel, amelyik nem mond semmit a tömegről, de meghatározza a spint és a töltést, viszont pont ezekről a tulajdonságokról nincs semmi információ. Bizonyítékról tehát szó sem lehet, sőt valójában az újabb eredmények szerint valószínű, hogy létezik az említettnél négyszer nagyobb tömegű részecske is, de akkor talán ez lenne a Higgs bozon? Vagy ez se? Az egész hókusz-pókusz csak arra volt jó, hogy felmutassanak valamit a gigantikus tudományos beruházásért: érdemes volt azt a sok pénzt és munkát befektetni, hiszen ez elősegítette a tudomány fejlődését. Ez nem jelenti azt, hogy Higgs koncepciója hibás lenne, de nem beszélhetünk bizonyítékról sem. Csak annyit mondhatunk, hogy az elemi részecskéket „katalogizáló” Standard Modell kiegészítésre szorul.

Kísérletek az elmélet kiszolgálói

A minél nagyobb energiával ütköztető gyorsító berendezések szükségességét avval indokolják, hogy evvel lehet igazolni bizonyos elméleti modelleket, így Higgs koncepcióját, vagy a szuperhúr elméletből fakadó szuperszimmetriát. Pedig ez az irányzat veszélyekkel jár, mert arra készteti a kutatókat, hogy mindenáron támasszák alá az előzetes elméleti koncepciót. A nagy energiájú folyamatok tanulmányozása valóban adhat lökést a mikrovilág jobb megismeréséhez, de célra vezetőbb, ha az elméletet igazítjuk az új kísérleti tényekhez és nem a fordított utat akarjuk bejárni. 

Mi a spin?

Nézzük meg, hogy valóban általános-e a kvantumelv a mikrovilágban. Ehhez azt kell először tisztázni, hogy mi a kvantum eredete. Ezt a kérdést nem veti fel a modern fizika, pedig ez a kérdés kulcsa. Korábbi írásaimban  („Térgörbület és gravitáció forgó rendszerekben”, „Fénysebességű forgások és a relativitáselmélet”, „A részecskefizika nyitott kérdései”)  már tárgyaltam ezt a témát, a legfontosabb megállapításokat itt összefoglalom. A kiindulópont a spin fogalma, ami megmutatja, hogy az elemi részecske saját impulzusnyomatéka hányszorosa a ℏ redukált Planck állandónak. Az elemi részecskék világában ez a legfontosabb összefoglaló fogalom, mert egyes elemi objektumok rendelkezhetnek nagyon különböző tömeggel, ami lehet nulla is (lásd a foton), lehet, hogy van töltésük (elektron, pozitron, kvark), de lehet a töltés nulla is (foton, neutrínó), viszont egy dologban megegyeznek: van spinjük, ami S = 1 a foton és S = ½ a többi felsorolt részecske esetében. Maga az impulzusnyomaték a forgó testek jellemzője, függ a test tömegétől, kiterjedésétől (például a sugarától) és a forgás frekvenciájától. Mivel az elemi objektumok rendelkeznek spinnel, így adódik a következtetés, hogy rendelkeznek tömeggel, sugárral is és forogniuk is kell. Evvel szemben áll, hogy a fotonnak nincs tömege, az elektron esetén pedig a pozitronnal való szórás kísérletekben (Bhabha szórás) azt találták, hogy a részecskék töltése egyetlen matematikai pontban sűrűsödik, azaz az elektron pontszerű. Emiatt a szakmai irodalom nem is beszél a részecskék forgásáról és úgy tekinti a spint, mint „intrinsic” tulajdonságot, ami van, de nem tudni, hogy miért.

Van-e tömege a fotonnak?

Próbáljuk először megérteni a foton esetét. A foton c sebességgel halad, a relativitáselmélet szerint a tömeg a sebességgel növekszik, minél közelebb van a sebesség c-hez a tömeg annál nagyobb lesz és ez a növekedési arány eléri a végtelent, ha az objektum sebessége a fénysebességgel egyenlő. Emiatt a foton „nyugalmi” tömege csak nulla lehet. Viszont a fotonnak van energiája, ami frekvenciájától függ: E = h.ν = ℏ.ω. A relativitáselmélet legfontosabb felismerése a tömeg és az energia ekvivalenciája: E = m.c². Tehát a fotonnak mégiscsak van tömege. Az ellentmondást úgy oldhatjuk fel, ha a határérték fogalmát használjuk. Ha egy szám határértékben végtelenhez tart, akkor reciproka nulla felé közelít, viszont a két szám szorzata ekkor is 1 (egy) lesz. Tekintsük hát a fotont a határértékben nullatömegű térpontnak, amit ha végtelenhez tartó növekedési aránnyal megszorzunk véges „mozgási” tömeghez jutunk: m = ℏ.ω/c². Más szóval a fénysebességű mozgás a tömeg és a vele ekvivalens energia forrása! Az energia kifejezésében a fénysebesség négyzete szerepel, ebből intuitíve arra gondolhatunk, hogy kétféle fénysebességű mozgás szükséges a tömeg létrehozásához. Erre a „második” mozgásra már azért is szükség van, mert magyarázni akarjuk az impulzusnyomaték eredetét, tehát a térpont nem csak „halad”, hanem forog is fénysebességgel. A foton energiáját egyetlen frekvencia határozza meg, az ω körfrekvencia, ezért ez határozza meg a forgás szögsebességét is. Mivel a c-vel egyenlő kerületi sebesség a sugár és a szögsebesség szorzata, a forgás sugara r = c/ω lesz.   Az impulzusnyomatékot megkapjuk, ha az impulzust, azaz p = m.c = ℏ.ω/c mennyiséget megszorozzuk a sugárral, tehát I = (ℏ.ω/c).( c/ω) = ℏ. Ily módon természetes magyarázatot kapunk a spin eredetére és egyúttal magyarázni tudjuk, hogy miért éppen a foton energiájában szereplő Planck állandó adja meg a foton frekvenciától független impulzusnyomatékát.

Az elemi körforgás centrifugális és centripetális ereje

Meggondolásainkban a klasszikus mechanika formalizmusát alkalmazzuk, mert nem a kvantumelv fogalmaiból akarunk eljutni valamilyen részecske modellhez, hanem  a kvantumok eredetét akarjuk tisztázni. A mechanika szabályai szerint minden körforgás során fellép a kifelé húzó centrifugális erő: F_cf = m.ω².r . A c kerületi sebességű forgásnál ez  F_cf  = m.c²/r értéket ad, ahol felismerhetjük a számlálóban a tömeg és energia ekvivalenciáját kifejező m.c²-et kifejezést. Ez annak felel meg, hogy a centrifugális erő a forgás kinetikus energiájához – ami viszont a „nyugalmi energia” eredete – kapcsolódik.  A centrifugális erő kifejezésébe írjuk be a tömeg m = ℏ.ω/c² kifejezését, az eredmény:  F_cf  = ℏ.c/r². Viszont bármilyen körforgás fenntartásához szükség van egy ellenerőre, amelynek nagysága egyenlő, de iránya fordított, mint a kifelé húzó centrifugális erő. Ennek neve a mechanikában a centripetális erő. 

Az erős gravitáció

Mi lehet a forrása az elemi forgások centripetális erejének? Ennek magyarázatához forduljunk az általános relativitáselmélet alapkoncepciója felé: a gravitációs erőt a tér torzulása idézi elő. A matematikai levezetés korábbi bejegyzésemben (lásd fent) már megadtam, itt most csak a vezérelvet emelem ki. Induljunk ki a Kepler által a bolygómozgásra felírt törvényből, ami a keringési idő (ez a frekvencia reciproka) és az átlagos keringési sugár között állapít meg összefüggést. Ezt a szabályt magyarázta meg Newton a tömegvonzás törvényének kimondásával, amiből az adódott ki, hogy a Nap körül keringő bolygók pályája nem függ a bolygó tömegétől, azaz végtelenül kis tömegű objektumok esetén is érvényes a szabály. Mivel a fénysebességű forgásmodell is végtelenül kis tömeget tulajdonít a tér pontjainak, így indokolt feltételezni, hogy a részecskék tömege körül is a tér Kepler forgásokat végez.. Ez a forgás virtuális és nem rendelkezik kitüntetett pályairánnyal, de valóságossá válik, amikor véges tömegű objektum keringéséről van szó. Nézzük meg, hogy mekkora tértorzulást okoz a Kepler forgás. A speciális relativitáselmélet kontrakciós szabálya szerint a mozgás irányában a távolságok lerövidülnek, körmozgás esetén a kör kerülete ezért nem a szokásos 2r.π szabállyal számítható ki, hanem annál kisebb lesz, a sugár viszont nem változik, mert a mozgásra merőleges irányban nincs rövidülés. A már említett bejegyzésekben kimutattuk, hogy mekkora a keringés miatti rövidülés és az ebből definiált tértorzulást figyelembe véve vezettük le Newton tömegvonzási törvényét. Ezáltal igazoltuk, hogy valóban a térpontok Kepler forgása a gravitáció eredete. De mi a helyzet fénysebességű forgások esetén? Ekkor extrém mértékű torzulás lép fel hiszen a kerület nullára zsugorodik! Evvel az extrém torzulással számolva azt kapjuk, hogy a centripetális erő F_cp  = – ℏ.c/r², tehát pontosan akkora, ami kompenzálni tudja a kifelé húzó erőt. Mivel ez az erő a gravitációval rokon, de annál sokkal-sokkal erősebb, ennek elnevezésére az erős gravitáció kifejezését használom.

Az elektron mint fénysebességű kettősforgás

Eddig a fotonnal foglalkoztunk, de mi a helyzet az S = ½ spinű részecskék, például az elektron esetén? Mi az oka a spin feleződésének, vagy miért tűnik az elektron pontszerűnek? Az elektronnak van nyugalmi tömege, ez megakadályozza, hogy fénysebességgel haladjon. Tételezzük fel, hogy az elektronnál, a fotonhoz hasonlóan kétféle fénysebességű mozgás kapcsolódik össze, de itt nem lehet szó c sebességű haladásról. Ebből adódik, hogy a második mozgás is forgás, amikor is a körforgás tengelye egy másodlagos fénysebességű forgást végez. Ez a kettős forgás a térben már egy gömbfelületet alkot. A második forgás az elsőhöz kétféleképp kapcsolódhat, ez megfelel a jobb és a balkéz viszonyának. Ezt a szimmetriát hívják kiralitásnak, ami a háromdimenziós tér alaptulajdonsága. Tehát kétféle részecske alakulhat ki, azaz kétféle anyag, az egyiket nevezzük anyagnak, a másikat antianyagnak. Ha az anyag és antianyag találkozik, akkor gammasugárzás kibocsátásával annihilál. Miért? Erre is egyszerű magyarázatot kapunk: mivel a második számú forgás a két esetben pont ellentétes, ezért kioltják egymást és csak az elődleges forgás marad meg, ez pedig nem más mint a foton! A kettős forgáshoz tartozik egy tehetetlenségi erő, amit Coriolis erőnek hívnak. Földi körülmények között erre példa, hogy a sarkoktól az egyenlítő felé haladó tenger és légáramlatok megcsavarodnak, de ezek forgási iránya épp ellentétes az északi és a déli féltekén. Az elemi részecskéknél ez a Coriolis hatás az elektromos töltés forrása, ami épp ellentétes az elektron és a pozitron esetén.

Az S = 1/2 spin eredete

Miért feleződik a spin? Mert a kettős forgás duplázza a centrifugális erőt, amit csak úgy tud ellensúlyozni a térgörbület, ha a forgási frekvencia kisebb lesz, ami viszont fele akkora impulzusnyomatékot generál. Miért pontszerű az elektron a szóráskísérletek szerint? Mivel mind a két forgás fénysebességű, így a felület nullára zsugorodik. A modell minden további elemi részecskére (neutrínó, kvarkok, a gyönge kölcsönhatást közvetítő bozonok) kiterjeszthető, evvel kapcsolatban a korábbi bejegyzésekre utalok.

Egydimenziós részecskék

Minden részecskét két fénysebességű mozgással értelmezve azt kapjuk, hogy elvész a felület, elvész két térbeli dimenzió, tehát minden elemi részecske egydimenziós alakzat. Ebben a tekintetben az általam kidolgozott részecskemodell hasonlít a húrelméletre, de óriási a különbség, mert ezt a dimenziót nem a három térbeli dimenzió bővítésével lehet megkapni, hanem fordítva, a három dimenzió csökkenésével egyetlen egyre.

Az egydimenziós részecskemodell összekapcsolható a Higgs féle szimmetriatörési koncepcióval is: elképzelhető, hogy a magas szimmetriájú euklideszi tér torzítása felel meg a szimmetriatörésnek, ami létrehozza a részecskék tömegét.

A kvantum eredete

További hozadéka a fenti modellnek, hogy a részecskék tömegének és spinjének magyarázatán kívül a kvantum eredetére is rávilágít: a kvantum eredete a fénysebességű forgás, amit ezért nevezhetünk a téridő elemi forgásának is. A ℏ Planck állandó a téridő alapvető szerkezeti eleme a c fénysebességhez hasonlóan. Amíg az utóbbi a térben történő hatások állandó határsebességét rögzíti, addig ℏ azt fejezi ki, hogy a tér fénysebességű forgása miatt létrejött torzulásához mekkora visszatartó erő tartozik és ehhez mekkora impulzusnyomaték járul. Az univerzumnak ez a két szerkezeti állandója a tér minden pontjában megegyezik, ami az egyes részecskék azonos impulzusmomentumában, töltésében és tömegében tükröződik.

A gravitáció kvantumelméletének kudarca

Miért nem lehet sikeres a szokásos gravitáció kvantumelmélete? Mert a gravitációs mozgás nem hozhat létre spint, pedig minden kvantumtér elmélet alapja a spin. A spin ugyanis fénysebességű forgást feltételez, a Kepler forgás viszont ezt a sebességet nem érheti el. Ily módon spinnel rendelkező közvetítő részecske sem alakulhat ki, más szóval a gravitációs erő nem jellemezhető kvantumokkal. Ugyanakkor az erős gravitáció a kvantum forrása, ezért nem a kvantumelv alapján kell eljutni a gravitációhoz, hanem fordítva: az erős gravitáció alkotja meg az elemi forgást, azaz a kvantumot.

Az univerzum kvantumelőtti állapota

A gravitáció az egyik terület, ahol nem érvényesül a kvantumelv, de ez határt jelent az Ősrobbanás elméletében is. Ezek az elméletek addig tekintenek vissza, ameddig a bizonytalansági elv megengedi, ez jelöli ki a Planck időt, amikor a bizonytalanság miatt nincs mit mondani az univerzum állapotáról.  De mi a garancia arra, hogy az univerzum korai fázisában is érvényes lenne egy olyan elv, ami a kvantumos felépítésből fakad? Hiszen amikor az ősi állapotban rendkívül gyors a kaotikus mozgás széttöredeznek a részecskéket alakító fénysebességű forgások is, amiért nem beszélhetünk kvantumokról sem. Ezért a Planck idő korszakhatár, kijelöli az univerzum kvantum előtti állapotát.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

A tér és idő fogalmának eredete

Az első részben már foglalkoztunk a téridő sajátságaival a kétréses kísérletek értelmezése során. Ott csak a kölcsönhatásban nem lévő fotonnal foglalkoztunk, itt most kibővítjük a redukált téridő fogalmát az elektronokra is. A redukált téridő a mikrovilág törvényeit határozza meg, a teljes téridő viszont a makroszkopikus világ értelmezési kereteit adja meg. Hétköznapi világunkban rengeteg információ ér minket, aminek hordozói elsősorban a fotonok, amelyek minden irányból és nagy távolságokból is szüntelenül érnek minket. Agyunk nagyszerű munkát végez, amikor összehasonlítja a különböző helyről érkező fotonok tulajdonságait és segít minket a tájékozódásban. Így alkotja meg azt a térfogalmat, ami jól elrendezi az információk sorát. Ebben az értelemben a tér fogalma, ami irányokból és távolságokból tevődik össze, jó összhangban van a kölcsönhatások terével, hiszen minden információ valamilyen kölcsönhatáshoz kapcsolódik. A másik fontos rendezési elv az idő, ami összegzi az események egymásutániságát, gyakoriságát, ismétlődéseit, valamint különbséget tesz az okok és a következmények között. Ahhoz már ki kell lépni a hétköznapi sebességek világból, hogy eljussunk a tér és idő fogalom összekapcsolásához, mert ennek hatása csak felfoghatatlanul nagy sebességeknél jelentkezik. Ezt az összekapcsolást alkotta meg a relativitáselmélet.

A mikrovilág pálya fogalma

 A másik nagy ugrás fizikai szemléletünkben azáltal következett be, hogy műszereink segítségével közvetlen kapcsolatba kerülhettünk a mikrovilággal, melynek törvényeit a kvantummechanika fogalmazza meg. Az elmélet körüli értelmezési vitákat főleg az okozza, hogy az elmélet matematikai kidolgozását nem követte a fogalmi rendszer következetes átértelmezése. A klasszikus fizika pályafogalma ugyanis átalakult a valószínűség fogalmának színrelépésével. Úgy is fogalmazhatunk, hogy a stacionárius pályán már nem azt a kérdést tesszük fel, hogy az objektum mikor ér el a tér egy adott pontjához, hanem azt, hogy mekkora valószínűséggel található meg ott, következésképp a pálya fogalma nem mozgást, hanem állapotot fejez ki. (Lásd még „Az intelligens elektron” c. bejegyzést.) Ha a mérés során a részecskét a tér valamelyik pontjában detektáltuk, akkor megszűnik annak a lehetősége, hogy bárhol másutt legyen. Ez nem jelenti azt, hogy ezáltal a fénynél gyorsabb változást idéztünk elő, mert a valószínűségi dimenzióban történő leírás nem keverhető össze az idő dimenzión alapuló pályafogalommal. Mivel az idő helyébe a valószínűség dimenziója lépett, így helyesebb a mikrovilágban már nem is téridőről, hanem tér-valószínűségről beszélni, amikor kötött állapotról van szó. Itt lényeges a kötött állapot hangsúlyozása, mert az elektromágneses mezőben mozgó elektron, vagy ionizált részecskék esetében a pálya továbbra is az idő függvénye, az energia pedig, nem diszkréten, hanem folytonosan változik. Fontos különbséget tenni a kölcsönhatás különböző szerepei között, stacionárius állapotban a kölcsönhatás – például a töltött részecskék közötti Coulomb vonzás – fenntartja, míg kvantumugrások esetén megváltoztatja az állapotot. A klasszikus fizikában ez a különbségtétel nem lép fel.

Rejtett idő és fázis a kvantummechanikában

Vajon teljesen elvész az idő a stacionárius kvantumállapotban? Nem erről van szó, hanem arról, hogy amikor stacionárius állapotról beszélünk, akkor nem vagyunk kölcsönhatásban a vizsgált mikro-rendszerrel. Ha kapcsolatba lépünk vele, akkor ez már az állapot megváltozását jelenti. De még ez előtt is „történik” valami, ami előttünk rejtve van. Ahogy a fotonnak is van egy „belső órája”, amelyik állandóan változtatja a fázist, de ezt csak az interferencia jelenségek során észleljük, úgy az elektronok és más elemi részecskék „órája” is ketyeg, de erről nem tudhatunk, hiszen a stacionárius állapot a kölcsönhatás hiányát jelenti. Ennek tudomásulvételéről van szó a kvantumelektrodinamikában (lásd később), amikor a fotonokat és az elektronokat is oszcillációként írja le. Minden stacionárius állapotnak van valamekkora energiája, ami meghatározza az oszcillátor frekvenciáját, de mi sohasem ezt a frekvenciát látjuk, csak ennek megváltozását, amikor az elektron ugrást végez két állapot között. Ez a frekvencia igazgatja a fázis periodikus változását, aminek általunk ismeretlen értéke határozza meg, hogy mikor következik be az elektronugrás két állapot között. Mivel számunkra ez a fázis ismeretlen, így csak valószínűségi kijelentéseket tehetünk az állapotváltozás bekövetkezésére. Ezt a valószínűséget hívja a kvantummechanika átmeneti valószínűségnek. A kvantummechanika tehát egy „praktikus” elmélet, mert válaszol minden kérdésre, amit mérhetünk, de nem ad útmutatást az előttünk rejtve maradó folyamatokról.

A kölcsönhatások hierarchiája

Az atomok összetevőinek világáról csak műszerek által közvetített információink vannak, és az elemi részecskékre csak korlátozott számú és minőségű kölcsönhatás hat. Természetesen az utóbbi megállapítás közelítés, ami azon alapul, hogy az elemi részecskék között csak a közvetlen szomszédságtól érkező kölcsönhatásokat vesszük figyelembe. Tudjuk azonban, hogy elvben minden objektum kölcsönhatásban van a teljes fizikai világgal, de ha ebből indulunk ki, akkor megoldhatatlanul bonyolult feladattal találkozunk. Ezért van szükség a kölcsönhatások hierarchiájának megállapítására. Ebben a hierarchiában megkülönböztethetünk fokozatokat és lépésről lépésre közelíthetünk az egyre pontosabb leíráshoz, de a teljeset, a valóságosat sohasem érhetjük el.

A makroszkopikus információk szerepe a mikrovilág tulajdonságainak feltárásában

A mikrovilágról nyerhető információ jellegét az információ hordozójának, a fotonnak a tulajdonságai határolják be. Erről az előző részben már írtam. Most csak azt emelem ki, hogy valójában sohasem egyetlen elemi objektumról szerezhető információt dolgozunk fel, ezt mindig kiegészítjük makroszkopikus ismeretekkel. Követhetjük például egyetlen részecske útját az emulzióban, vagy a ködkamrában, de ekkor azért láthatjuk az ionizáló sugárzás nyomát, mert a nagy energiájú részecske mozgása során nagyszámú molekula szerkezetét változtatja meg, ami „nyomot” hagy. Erről a nyomról pedig nagyszámú foton ad hírt, amikor vizsgáljuk a részecske pályáját. Tehát amikor egyetlen részecske tulajdonságaira következtetünk, akkor hallgatólagosan felhasználjuk azt a tudást, amit a makroszkopikus világ nyújt számunkra. Ugyanez a helyzet a korábban tárgyalt kétréses kísérletben is, ahol a térről szerzett tudást a műszerről szerzett ismereteink biztosították. Amikor a foton, vagy egy elektron pályáját a kölcsönhatás előtti időszakban akarjuk jellemezni, nem állnak rendelkezésre térbeli irányok és távolságok, amihez hasonlítani tudnánk a mozgási pályát, arról sincs információnk, hogy épp hol tartózkodik a részecske.  Viszont amikor a fotont, vagy elektront detektáljuk, akkor látjuk azt a helyet, ahol a kölcsönhatás megtörtént és tudhatjuk annak időpontját is. Ezek azonban makroszkopikus információk.

A kvantumelektrodinamika szemléletmódja

A kvantumelektrodinamika leírja a fotonok és elektronok állapotát, abban az időszakban is, amikor nincs még észlelhető kölcsönhatás. A leírásban a szokásos (makroszkopikus) tér és idő fogalmát használjuk. Ennek elmélete a kvantumelektrodinamika, melyben a fotonok és elektronok együttes rendszerét vizsgáljuk, ahol a mozgásokat és kölcsönhatásokat a foton és elektronok számának változásával jellemezzük. Ez a mezőelméleti megközelítés alkalmasabb a mikro-rendszer állapotának és folyamatainak leírására, mint az elektronok  állapotát önmagában vizsgáló kvantummechanika, mert itt a fotonok a kvantumfolyamatok egyenrangú résztvevőivé válnak. A módszer sajátsága, hogy a fotonokhoz és elektronokhoz egyaránt oszcillációkat rendel. Az általam javasolt fénysebességű forgásmodellel ez teljes összhangban van, mert a forgások vetületi képei oszcillációnak felelnek meg. A ténylegesen kibocsátott és elnyelt fotonokon kívül a mezőelmélet virtuális fotonokról is beszél, melyek szerepe a töltött részecskék (például az atommag és az elektronok) közötti elektromos és mágneses mező létrehozása.  A legkülönösebb az elméletben, hogy megenged fénynél sebesebb mozgásokat, virtuálisan létrejövő elektron-pozitron párokat, sőt az idő megfordulását is, amikor előbb veszi figyelembe az elektron-pozitron pár hatását, mint amikor létrejött. A furcsa jelenségek oka, hogy a kölcsönhatás előtti állapotban a tér és idő fiktív matematikai dimenzió, így minden lehetséges folyamat megengedett, sőt szükséges, amit csak a matematikai feltételek megkívánnak.

A redukált téridő

A kölcsönhatás nélküli eset fiktív térideje és a makroszkopikus téridő a két végletet képviseli, az utóbbit nevezhetjük a teljes téridőnek. Az atomok és molekulák leírásában bevezethetjük a redukált téridő fogalmát, amikor az elektromágneses kölcsönhatásokat figyelembe vesszük, melyek aztán információt adnak a tér szerkezetéről. Másképp fogalmazva, az elektronok teréről csak annyi információnk van, amennyit az elektronok kölcsönhatásai nyújtanak. Ennek első példája legyen a hidrogén atom, ahol egyetlen elektron „kering” (pontosabban tartózkodik) a proton körül. Ekkor az elektromos mező kizárólag a proton és elektron távolságától függ, az irányok között pedig nem lehet különbséget tenni. Ennek leírásához két módszert használhatunk. Ha a szokásos teljes téridővel írjuk le a mikro-állapotot, akkor az állapotot jellemző függvényben minden irányhoz azonos valószínűségi amplitúdót kell rendelni (a valószínűséget az amplitúdó abszolút értékének négyzete adja meg a kvantummechanikában). De bevezethetjük a redukált tér fogalmát is, amikor a teret csak az elektron-mag távolság jellemzi (ez a radiális paraméter) és nem szerepel benne az irány. A két felfogás között a kvantummechanika hidat teremt, mert bevezeti a szuperpozíció fogalmát. Ez azt jelenti, hogy az állapotfüggvény a különböző irányokhoz tartozó állapotok szuperpozíciója. Az egyes állapotokat két kvantumszámmal lehet jellemezni, melyek közül az első a radiális eloszlás maximum helyeinek számát, a másik pedig az impulzusnyomaték nagyságát adja meg (lásd „Miért diszkrétek az energiaállapotok kötött állapotban I-V). Vannak olyan állapotok, melyben az impulzusnyomaték nulla (ezeket nevezik s pályáknak), ekkor az impulzus mindig a centrum felé mutat, vagy avval épp ellentétes irányú, ami a centrumon áthaladó lineáris oszcilláció pályájának felel meg. Az s pálya ezeknek a lineáris oszcillációknak a szuperpozíciója. Tehát a gömbszimmetrikus s pálya nem azt jelenti, hogy a mozgás során az elektron minden irányba eljut, hanem arról van szó, hogy az irány fogalmának hiánya miatt minden irányban azonos valószínűség jellemzi a mikro-állapotot.

Impulzusnyomaték és az atomi pályák

Az elektron olyan pályákon is tartózkodhat, ahol az impulzusnyomaték nem nulla, például lehet ℏ (p pályák), vagy 2ℏ (d pályák) is. A pályacsaládok függvényeit a forgatások átviszik egymásba, a független pályák száma három a p és öt a d pályák esetében. Az irányok definiálatlansága abban nyilvánul meg, hogy az említett függvényterekben nincs kitüntetett pálya, egyenértékű bármelyik szuperpozíció, amennyiben az amplitúdók négyzeteinek összege kiadja az egységnyi, tehát a teljes valószínűséget. Ezek a pályák elkerülik a centrumot és egymástól elhatárolt valószínűségi tartományokból állnak, ahol a határokon nulla a valószínűség. A klasszikus gondolkodás felveti a kérdést, hogyan közlekedhet két tartomány között az elektron, ha az átmeneti régióban egyáltalán nem lehet?  Tipikus kérdés, ami hibásan keveri a klasszikus és kvantumfogalmakat. Az elektronnak nem kell „közlekedni” a tartományok között, mert a pálya nem időbeli, hanem a valószínűség dimenziójában felépülő fizikai entitás.

Elektronpályák a molekulákban

Lépjünk tovább a molekulák világába és vizsgáljuk például a metán molekulában a szénatomban lévő elektronokat. Milyen lesz a redukált tér fogalma, amit az elektronok érzékelnek? Mivel a szén atommagján kívül az elektromos mezőt a tetraéder négy csúcsán levő hidrogénatomok is befolyásolják, a tetraéder csúcsainak iránya kitüntetett lesz. Más szóval bővül a redukált tér fogalma, amivel az elektronpályákat leírjuk, de még nem lesz teljes. Ennek oka, hogy nem tehetünk különbséget a négy hidrogén atom között. Matematikailag ezt a csoportelmélet segítségével vehetjük figyelembe, támaszkodva a tetraéder összes szimmetriaműveletére, aminek segítségével meghatározhatjuk a szuperpozíciós együtthatókat (valószínűségi amplitúdókat), amelyekkel szorozni kell az egyes s, p, d függvényeket, hogy felépítsük az elektronpályát. A számításban először csak a legerősebb kölcsönhatással foglalkozunk az elektronok és a szén atommag között, ezt egészítjük ki második lépésben az elektronok közötti kölcsönhatással, majd a harmadik lépésben kerül sor a hidrogén atomok perturbáló hatására. Ez felel meg annak, hogy a tér fogalmát bővítjük ki lépésről lépésre. Nagy molekuláknál, ahol már nincs geometriai szimmetria, a mikro-rendszer térfogalma már azonos lesz a makroszkopikussal, mert minden térirányban különbözik az elektromos mező. Még ebben az esetben is fennmarad egy szimmetria, ami az elektronok megkülönböztethetetlenségéből következik. Emiatt az elektronpályákat permutálni kell (determináns hullámfüggvény), és különböző matematikai közelítő eljárások révén lehet meghatározni az elektronok egész molekulára kiterjedő pályafüggvényeit. Nem célom az eljárások bemutatása, csak azt akarom kihangsúlyozni, hogy az elektronok nem lokalizálódnak az egyes atomokban, sőt kémiai kötésekben sem, hanem kiterjednek az egész molekulára. A mikrovilágban minden, ami megkülönböztethetetlen a kvantummechanikában mint szuperpozíció jelenik meg, és ezért lesz az elektron molekulapályája az egyes atompályák szuperpozíciója.

Záró gondolatok

A kvantummechanika különös szemléletmódja két alapvető okra vezethető vissza, amelyeket különböző példákon mutattam be négy részletben. Az egyik ok a foton szerkezetéből fakad, a fotonok által nyújtott információ korlátozott, mert a hullámhosszra és az impulzusra, illetve a frekvenciára és az energiára vonatkozó szabályok össze vannak kötve a Planck állandó és a fénysebesség állandósága miatt. A másik fontos tulajdonság, hogy minden foton azonos impulzusnyomatékkal rendelkezik, amely szintén a Planck állandóval egyezik meg. A kvantummechanika másik sajátsága, hogy a mikro-rendszereket, például az elektront magában foglaló térről csak annyit tudhatunk meg, amennyit a ráható kölcsönhatások szimmetriája megenged. Ehhez járul még az elektronok megkülönböztethetetlensége.

Az idő látszólag elvész, amikor stacionárius állapotról beszélünk, de rejtve mégis jelen a fázis formájában, ami majd akkor ad életjelet magáról, ha a stacionárius állapot megváltozik. Ez a jelenség okozza, hogy az átmenetek bekövetkezésének ideje helyett, csak annak valószínűségét mondhatjuk meg. Ez okozza a determinizmus hiányát a mikro-folyamatokban, ami azonban látszólagos, csupán a fázis értékének ismeretlenségét tükrözi.

Ezek a tulajdonságok jelennek meg a kvantummechanikában, melyben a fizikai mennyiségek operátorai, mint hatások jelennek meg, melyek vagy fenntartják, vagy megváltoztatják a mikro-rendszer állapotát. Ha szem előtt tartjuk ezeket az elveket, akkor közelebb juthatunk a mikrovilág rejtélyeinek megértéséhez.

További írások elérhetők: Paradigmaváltás a fizikában...

A kvantum felfedezése és a foton

A mikro-rendszerek energiájának ugrásszerű változása elválasztja egymástól a klasszikus és a kvantummechanikát. A klasszikus fizikában minden fizikai mennyiség értéke folytonosan változik, a kvantummechanikában ez másképp van. Az atomok színképvonalai arra utalnak, hogy az elektronok diszkrét energianívók között végeznek ugrásokat. A kvantummechanika kialakulásának kezdő lökését Planck adta meg, amikor a XIX. század fordulóján kifejtette nézetét a fény kvantumos természetéről. Ennek oka a fekete test sugárzásának értelmezése volt. A sugárzás frekvencia eloszlása a kis energiák tartományában a végtelenhez fut, ha a fekete test által kisugárzott energia egy adott hullámhosszon tetszőlegesen kis intenzitású lehet. Planck feltételezése szerint a monokromatikus, tehát azonos hullámhosszú sugárzás intenzitását fokozatosan csökkentjük, akkor eljutunk egy határhoz, ami alatt már nem osztható tovább az intenzitás, mert a további csökkentés már a fény megszűnését okozza. Van tehát a fénynek egy legkisebb egysége, amit később a fény kvantumának, fotonnak neveztek el. A foton energiája arányos a ν frekvenciával, melynek értéke E = h.ν, ahol h a nevezetes állandó, amit aztán Planckról neveztek el. A foton valamennyi tulajdonságát egyetlen mennyiség, a frekvencia határozza meg, mert a fénysebességű mozgás miatt a hullámhossz λ = c/ν, az impulzus pedig a hosszúság egységre jutó hullámok számával, tehát 1/λval arányos, azaz p = h/λ. Ezt az utóbbi összefüggést érdemes úgy is felírni, hogy λ.p = h. Ennek majd a bizonytalansági elv megértésénél lesz jelentősége. A vizsgálatok azt is kimutatták, hogy a foton impulzusnyomatékkal is rendelkezik, melynek értéke független a frekvenciától és ezt is a redukált Planck-állandó határozza meg: ℏ = h/2π.

A monokromatikus fény energiája tehát nem folytonosan, hanem h.ν lépésekben változik, és azt fejezi ki, hogy a sugárzás hány fotont tartalmaz. Más oldalról viszont folytonos az energia változása, mert a frekvencia, és vele együtt a már említett egyéb tulajdonságok folytonosan, azaz ugrások nélkül változnak.

Elektronmozgás az atomban: a Bohr modell

A kvantummechanika felé a másik fontos lépést Bohr tette meg, aki megalkotta az atom „bolygó” modelljét. Ebben a modellben a negatív töltésű elektronok körpályán mozognak a pozitív töltésű atommag körül és az atomok sugárzásához tartozó színképvonalak a körpályák közötti energiaugrásoktól származnak, ahol az E₁ – E₂ = h. ν szabály határozta meg a kibocsátott foton frekvenciáját. Bohr ebben a modellben az egyes pályákat az impulzusnyomaték segítségével definiálta, amelynek értékét a redukált Planck-állandó egészszámú többszöröse adta meg. Ez a szabály tehát magyarázta az energia ugrások eredetét, de ellentétes volt az elektrodinamika Maxwell-féle törvényével, amely szerint a gyorsuló pályán mozgó töltések folytonos sugárzást bocsátanak ki, márpedig a körmozgás állandó gyorsulással jár. A folytonos sugárzás hiányát avval magyarázta, hogy vannak kivételes pályák, melyek impulzusnyomatéka ℏ egészszámú többszöröse, ahol nem sugároz a keringő elektron és ezeket a pályákat stacionáriusnak nevezte el. A modell alapvető újdonsága, hogy folytonos energiasugárzás helyett kvantumokban történő foton kibocsátást tételez fel. Bár a későbbi vizsgálatok túlhaladták a Bohr-modellt, mégis úttörő jelentőségűnek bizonyult az elképzelés, egyrészt a stacionárius állapotok, másrészt a kvantumos energia kibocsátás fogalma miatt.

Ugrásszerű változások és a matematikai operátorok

A XX. század első harmadában a fizikusoknak egy új feladattal kellett megbirkózniuk. Newton óta rendkívül sikeresen lehetett alkalmazni a folytonosság elvén alapuló fizikai fogalmakat a differenciálszámítás segítségével. Hogyan lehet ezt úgy kiterjeszteni, hogy alkalmas legyen az ugrásszerű változások leírására is?

 A végül megtalált matematikai eljárás megértéséhez induljunk ki a különböző fizikai fogalmak definíciójából! Mi is az impulzus? Az a fizikai mennyiség, ami fenntartja az állandó sebességű, egyenes vonalú mozgásokat. Mi az impulzusnyomaték: ami fenntartja a forgást, és mi az energia: ami az állandóságot képviseli a változó sebességű mozgásokban. Tehát a felsorolt fizikai mennyiségek fenntartják, nem pedig megváltoztatják a vizsgált fizikai rendszerek állapotát. Tehát a fizikai mennyiségek reprezentálásához olyan matematikai eszközre van szükség, ami a mikro-rendszer állapotát leíró függvényt megtartja, azaz nem változtatja meg. Vezessünk be ezért valamilyen függvényt, ami az állapotot jellemzi, és erre hasson az a matematikai eszköz, ami változatlanul hagyja ezt a függvényt, amennyiben megfelelően írja le a mikro-rendszert, de változtassa meg az ellenkező esetben, amikor a választott függvény nem írja le helyesen a vizsgált rendszer állapotát. A fizikusok szerencséjére ezt a matematikai eszközt, amit operátornak neveznek, a matematika már kidolgozta. Ebben az eljárásban a különböző függvényekhez, amit sajátfüggvényeket neveznek, az operátor különböző értékei (sajátértékek) tartoznak, melyek akár diszkréten, akár folytonosan változhatnak.

A fizikai mennyiségek operátorai

A fizikai mennyiségeknek megfelelő operátorokat Schrödinger és Heisenberg alkotta meg, és egyenleteik segítségével indult hódító útjára a fizika új elmélete, amit kvantummechanikának nevezünk. Az elmélet sikereit annak köszönheti, hogy a hatás oldaláról jut el a fizikai mennyiségek matematikai leírásához, a hatás pedig azonos akár a makro- akár a mikrovilágról van szó.  Annak logikáját, hogyan lehet eljutni az egyes fizikai mennyiségek operátoraihoz már bemutattam egy korábbi bejegyzésben („Út a kvantummechanika megértéséhez”). Érdemes megjegyezni, hogy az erő fogalmához a kvantummechanika nem rendel közvetlenül operátort. Ennek oka, hogy az erő nem állapotfenntartó, hanem állapotváltoztató fizikai fogalom! Az erő definíciójához közvetve juthatunk el vagy a potenciális energia térbeli, vagy az impulzus időbeli változásán keresztül.

Diszkrét energiaállapotok kötött rendszerekben

Diszkrét energiájú állapotok kizárólag kötött rendszerekben jelennek meg, ha az elektron szabad pályán mozog, akkor energiája folytonosan változtatható akár elektromos, akár mágneses tér alkalmazásával. Két speciális erőtérben már részletesen bemutattam a diszkrét nívók kialakulását („Miért diszkrétek az energianívók kötött állapotban, I-V”). Ott konkrét kvantummechanikai számításokat mutatok be összehasonlítva a klasszikus mechanika módszertanával. Ebben a bejegyzésben viszont a levonható elvi következtetéseket emelem ki. Két alaptípusát vizsgálom a kötött rendszereknek, az egyik az atomban mozgó elektroné, a másik a molekulában a kémiai kötésben levő atomok vibrációjával foglalkozik. Az első esetben az erő a távolsággal csökken, a másik eset épp fordított, ott a távolság függvényében növekszik a visszahúzó erő. Az első esetben a potenciális energia a centrumban végtelenhez tart, a másokban pedig nulla az egyensúlyi helyzetben. Tehát a két rendszer éppen ellentétes esetét képviseli a kötött állapotnak.

Rezonancia jelenség, mint a diszkrét állapotok oka

Mindkét esetben a mikro-rendszer energiájának diszkrét változását a fotonokkal való kölcsönhatás okozza, amit a fotonok és az atomok, illetve elektronok mozgása közötti rezonancia vált ki. Molekulavibráció esetén a vibráció és a foton frekvenciájának egybeesése vezet rezonanciához, míg az elektron átmeneteknél a különböző energiákhoz rendelhető frekvenciák különbsége egyezik meg a foton frekvenciájával. Vibrációkban mindig ugyanakkora energia felvételre, vagy leadásra kerül sor a rezonancia miatt, azaz nem a molekuláknak van „megtiltva”, hogy a vibráció energiája folytonosan változzék, hanem az elnyelt, vagy kibocsátott fotonok azonos energiája épít fel diszkrét és ekvidisztans energiaállapotokat. Egy hasonlattal élve képzeljük el, hogy egy víztartály töltünk fel és mindig egy-egy teljes vödör vizet öntünk a tartályba. Ekkor a vízszint mindig pontosan azonos mértékben emelkedik. De ha nem egész vödör vizet öntenénk be, akkor a vízszint folytonosan és nem diszkrét egységekben változna. A másik példában, amikor az atommag körül keringő elektron energiaszintjeiről van szó, a foton mindig egységnyi impulzusmomentumot közöl a rendszerrel, vagy vihet el az elektrontól, és emiatt csak olyan nívók alakulnak ki, amelyek impulzusnyomatéka a redukált Planck állandó egész számú többszöröse. Ez viszont már meghatározza az egyes nívók diszkrét energiáját, melyek között rezonanciaszerű átmenetek jöhetnek létre. 

Folytonos változás az ugrások között

Az elmondottak értelmében a kötött állapotú mikroszkopikus rendszerek energiája is folytonosan változhat, de a fotonok rezonanciaszerű kölcsönhatása miatt diszkrét vonalak jelennek meg mind a vibrációs, mind az elektron színképben. Minden fizikai mérésben a fotonok szállítják az információt a vizsgált rendszer állapotának megváltozásáról és ez alapján következtetünk a rendszer állapotára. Kérdés, hogy van-e olyan kísérleti bizonyíték, ami alátámasztja az energia folytonos változását? A válasz igen! A megfigyelt színképvonalak ugyanis sohasem végtelenül élesek, minden vonal véges szélességgel (eloszlással) rendelkezik, így ha jóval kisebb intenzitással, de a diszkrét vonalak között is detektálható átmenet. A kiszélesedés oka a bizonytalansági reláció, ami szintén a fotonok tulajdonságaiból következik.

A fotonoktól származó információ és a bizonytalansági relációk

A jelenséget egy a Rákosi korszakból származó rendőrviccel szemléltetem. A kérdés, miért járőrőznek a rendőrök hármasával? A válasz, hogy az egyik rendőr csak írni, a másik csak olvasni tud. De miért van szükség a harmadikra? Mert ő ellenőrzi a két „intelligenciát”. Hasonló a helyzet a fotonokkal is, vagy a pozíciót, vagy az impulzust tudják pontosan meghatározni. A bevezetésben már említettem, hogy a foton hullámhosszának és impulzusának szorzata épp a Planck állandó. Amikor valamit mérünk szükség van egy skálára és a skálabeosztás finomsága határozza meg a mérés pontosságát. Felhasználhatjuk a fotont a hely, a pozíció mérésére, ekkor a skálabeosztásnak a foton hullámhossza felel meg, de felhasználhatjuk az impulzus mérésére is, ekkor h/λ fogja limitálni a mérés pontosságát. A két hiba pontosságának szorzata ezért h lesz. De miért ne használhatnánk két fotont, az egyiknek legyen kicsi a hullámhossza, a másiknak nagy. A probléma, hogy az első foton a rövid hullámhossz és a nagy impulzus miatt erősen megváltoztatja az elektron, vagy a molekula impulzusát és a második foton már egy megváltozott állapot impulzusáról ad felvilágosítást.  És mi van a vicc harmadik rendőrével? Hát ő a fizikus, aki az információt feldolgozza.

A bizonytalansági reláció másik formája a méréshez rendelkezésre álló időt és az energiamérés pontosságát hozza kapcsolatba. Ha vizsgálunk egy molekulát folyadékban, akkor a molekula csak addig tartózkodik egy megadott állapotban, amíg egy másik molekulával való ütközés nem változtatja meg a tulajdonságait. Ezért amikor felvesszük a színképet fontos szerepe van annak az időtartamnak, amíg a molekula változatlannak tekinthető. Ez azt jelenti, hogy a molekula által kibocsátott, vagy elnyelt frekvencia értékét modulálja az ütközési gyakoriság. A frekvencia modulációja viszont az energiamérés pontatlanságával jár együtt, ami a színképeken a vonalak kiszélesedésében nyilvánul meg.  Az ütközések között eltelt időt szorozva az energiamérés pontatlanságával ismét megkapjuk a Planck állandót.

A nullponti vibráció fizikai oka

A bizonytalansági reláció sajátos megjelenési formája a nullaponti rezgés. Ha melegítünk egy testet, akkor a vibrációk intenzívebbé válnak, ha hűtjük, akkor csak alacsonyabb energiájú vibráció jön létre. Azonban bármennyire is hűtjük a vizsgált tárgyat a vibráció soha sem fagy be teljesen. Ezt hívjuk nullaponti vibrációnak, ahol a nulla az abszolút nulla fokot jelenti a Kelvin skálán. Mi ennek az oka? Ha teljesen megszűnne a vibráció, akkor tetszőleges pontossággal mérhetnénk a pozíciót, miközben az impulzusról tudnánk, hogy nulla, ami ellenkezne a bizonytalansági elvvel. Ez az alapállapotú vibráció azonban már nem bocsát ki fotonokat, csak gerjeszthető magasabb energiájú állapotba, hatása mégis megfigyelhető a Röntgen- vagy neutron diffrakciós szerkezetvizsgálatban, amit az egyes atomok pozíciójának elmosódottsága mutat.

Elektron az atommag belsejében

Az elektronok mozgásánál az atomban szintén a bizonytalansági elvvel magyarázható, hogy még a végtelen mélységű elektromos potenciál sem képes az atommagban tartani az elektront. A nulla impulzusmomentumú pályán azonban véges valószínűséggel a magban is előfordul az elektron. Ez mérésekkel is kimutatható, mert meghatározható az elektron és az atommag között egy irány független mágneses kölcsönhatás. Másik eset, amikor néhány radioaktív izotópban, ahol a protonok relatív száma magas, az elektron egyesülhet a protonnal létrehozva egy neutront és egy neutrínót (K-befogás). Ekkor már az elektron teljes egészében, tehát nem csak egy tört valószínűséggel, az atommagban tartózkodik. Ez látszólag ellentmond a kvantummechanikának, de csak látszólag, mert az elektron ekkor megszűnik eredeti formájában létezni és így az állapotára vonatkozó bizonytalansági törvény már nem érvényesül. Az elektron és a proton kölcsönhatását nem az elektromágnesesség, hanem egy rövidtávú hatás, az un. gyenge kölcsönhatás idézi elő.

Link a folytatáshoz: A kvantumvilág rejtélyei 4.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

Az EPR-paradoxon

Több szálon fut a kvantummechanikai bizonytalansági elv értelmezése. Addig egyeznek az álláspontok, amíg nagyszámú részecske tulajdonságairól van szó, mert ekkor elfogadható a valószínűségekre alapozott statisztikai leírás. A kvantummechanikai korrespondencia elv szerint a határozatlansági törvények belesimulnak a makro-világban a klasszikus fizika determinizmusába. Más a helyzet, ha egyetlen foton, vagy elemi részecske tulajdonságait vizsgáljuk. Erre példa az Einstein, Podolsky és Rosen által felvetett gondolatkísérletek esete (EPR-paradoxon), melyek közül néhányat már tényleges kísérlettel is ellenőriztek.

A jelenséget két nagyon egyszerű esettel fogom szemléltetni. Ha egy üveglapra fényt bocsátunk, akkor annak négy százaléka onnan visszaverődik és 96 százaléka áthalad. Ha a fény fotonjait egyesével vizsgáljuk, akkor egymásután 100 fotonból négy fog visszaverődni és 96 halad át rajta. De mi dönti el, hogy egy kiválasztott foton esetén mi fog történni? A másik példa a neutronbomlás esete. A kísérletek szerint a szabad neutronok negyedóra alatt bomlanak el, amikor az átalakulás során egy proton képződik egy-egy elektron és (anti)neutrínó kiválása mellett. Ha nagyszámú neutront vizsgálunk, akkor a bomlási idő egy statisztikai paraméter, de ha kiválasztunk egyetlen neutront, akkor nem tudjuk, hogy mikor fog bomlani. Lehet, hogy azonnal, lehet, hogy félóra múlva, de az is lehet, hogy napokat, hónapokat kell várni, amíg a bomlás bekövetkezik. A kvantummechanika csak valószínűséget ad meg, de az egyes fotonok, részecskék sorsáról nem ad felvilágosítást. Mi dönti tehát el az egyes fotonok, részecskék sorsát? Eszerint a mikrovilág folyamatait a véletlen irányítaná és csak a makroszkopikus folyamatokban uralkodnának determinisztikus törvények?

 A tudományos megismerés Galilei kritériumai

A tudományos gondolkozás alapjait még Galilei fektette le három pontban: (Párbeszédek: a két legnagyobb világrendszerről, a ptolemaiosziról és a kopernikusziról, 1632, Firenze) 

1. Léteznek matematikai formulákkal leírható általános természeti törvények
2. A törvényeket tudományos kísérletek segítségével kell megállapítani
3. A kísérleti eredmények tökéletesen reprodukálhatók

Galilei módszertana ma is a tudományos kutatás alapelve. Minden kísérletnél törekedni kell az azonos feltételek biztosítására, hiszen e nélkül nem lehet reprodukálhatóság. Ennek megvalósítása azonban még a klasszikus fizika körülményei között is nehézségekbe ütközik. Vegyünk egy egyszerű példát, például a nehézségi gyorsulást akarjuk meghatározni. Mérhetjük azt az időt, ami alatt egy tárgy leesik egy bizonyos magasságról. A mérés pontossága azonban megköveteli, hogy kizárjunk bizonyos tényezőket. Mindenekelőtt a kísérletet vákuumban kell végrehajtani, hogy elkerüljük a légellenállást. Azt is figyelembe kell venni, hogy a Föld különböző pontjain más és más a gravitációs erő. Ha nagy pontosságra törekszünk, akkor standardizálni kell a hosszúságmérést (például a hőmérséklet megváltoztatja a mérő rúd hosszát) és gondoskodnunk kell arról, hogy a leejtés és az érkezés idejét pontosan tudjuk megfigyelni. Nagy pontosságnál még az évszak is számít, mert a Föld keringéséből származó centrifugális hatás is szerepet játszik, sőt még a napszak sem közömbös, mert a Nap és a Hold helyzete is fontos gravitációs hatásuk miatt. A mérést tehát „steril” körülmények között kell végezni. Valójában még így is lesznek figyelmen kívül hagyott finom effektusok.

A mérésnél ki kell zárni a szubjektív hatásokat, nem szabad, hogy a mérést végző „ügyessége” befolyásolja az eredményt, más szóval az eredménynek objektívnek kell lenni. A legnagyobb hiba, amit a kísérletező elkövethet, ha önkényesen kizárja a „váratlan” eredményeket, ami nem illeszkedik az előzetes elmélet keretei közé. Hibát még a legnagyobb körültekintés ellenére is könnyű elkövetni, akár a mérésnél, akár a kiértékelésnél és ez különösen igaz, amikor a mikrovilág jelenségeit kutatjuk. Csak egy példa rá a közelmúltból. Megjelent a hír, hogy a neutrínók sebességmérésénél a fénysebességet meghaladó értéket kaptak, azonban utólag kiderült, hogy egy tényezőt figyelmen kívül hagytak és emiatt lett hibás az eredmény.

Kiegészíthető-e a kvantummechanika rejtett paraméterrel?

Fölvethető a kérdés, vajon nem a reprodukálhatóság hiánya miatt lép fel a valószínűség fogalma, amikor a mikrovilág jelenségeit értelmezzük? Vagy az elméletből hiányzik valami? Einstein végig vitatkozott avval az állásponttal, hogy a mikrovilágban a véletlen határozná meg az események sorsát, nevezetes mondása szerint „Az Isten nem kockajátékos”. Emiatt jutott arra a következtetésre, hogy a kvantummechanika nem teljes elmélet, kell lennie valamilyen rejtett paraméternek, amelyik eldönti, hogy mi történik a mikro-folyamatokban.

Gondolatkísérletek egyedi fotonokkal

Nézzünk meg néhány példát az EPR-paradoxonra, foglaljuk össze az evvel kapcsolatos nézeteket és kíséreljük meg a jelenségek újraértelmezését. A szóban forgó a példák többnyire elképzelt un. gondolatkísérletek, bár hála a technikai fejlődésnek, néhányat már sikerült megvalósítani. Vetítsünk fényt egy üveglapra és helyezzünk el két detektort, az egyik vizsgálja a visszavert fényt, a másik pedig, ami áthalad az üveglapon. Ha egyesével lőjük ki a fotonokat, akkor mindig csak a két detektor egyike adhat jelet. Erre a példára már utaltunk az előzőekben. De válasszunk egy összetettebb elrendezést! Legyen a foton forrás egy gömb középpontjában és helyezzünk el minden irányban detektorokat. Ekkor is, ha egyetlen fotont bocsátunk ki, csak egyetlen detektor adhat jelet. Az einsteini nézőpont szerint a két példa azt bizonyítja, hogy a kvantummechanika nem teljes, szükség lenne rejtett paraméterekre. A koppenhágai iskola viszont avval érvel, hogy a kvantummechanikai kép a detektálás előtt a potenciális valóságot írja le, míg a detektálás pillanatában a hullámfüggvény redukálódik és a lehetséges állapotok közül egyetlen egy valósul meg. Ez a magyarázat azonban nyitva hagyja a kérdést: hogyan valósul meg ez a rejtélyes redukció, honnan tudja a sok néma detektor, hogy hallgatnia kell?

Interferencia jelenségek a mikro-folyamatokban

Ha a fotonok interferenciáját leíró hullámmechanikai képet kiterjesztjük a fotonok és elektronok kölcsönhatásának leírására és újragondoljuk a térről és időről alkotott fogalmainkat a mikrovilág folyamataiban, akkor megérthetjük a jelenséget. A foton hullámtermészetét leíró matematikai függvényben szerepel a frekvencia és a fázis: exp(iφ) = exp(i(ωt+φ₀)). A fázisnak fontos szerep jut a fényinterferencia leírásában. Sikerült kísérletileg bizonyítani, hogy nem csak a foton, hanem az elektron, az atomok és a kisebb molekulák is interferenciát hoznak létre, azaz rendelkeznek hullámtulajdonságokkal.. Ez azt jelenti, hogy az elektron sajátmozgásához is rendelhető egy frekvencia, amit a tömege határoz meg és egy Φ fázis. A foton és az elektron fázisának egyezése a kölcsönhatások egyik feltétele. A kölcsönhatás rezonancia jellegű, ami két elektron nívó közötti ΔE energiakülönbség és a foton energiájának egyezését kívánja meg, melynek értelmében a foton frekvenciája ω = ΔE/ℏ, ami megegyezik a két energiaállapothoz rendelhető frekvencia különbségével, azaz ΔΩ = ω. A ΔΩ frekvencia különbség periodikusan változtatja az elektron hullámfüggvényének relatív fázisát:ΔΦ = ΔΩ.t összefüggés szerint. A rezonancia létrejöttéhez az is szükséges a frekvenciák egyezésén kívül, hogy a fáziskülönbség nulla, vagy ahhoz közeli értékű legyen. Ez mutatkozik meg a spontán emisszió jelenségében, amikor a gerjesztett állapotú elektron alacsonyabb energiájú pályára ugrik foton kibocsátása mellett. Abból kiindulva, hogy a foton és elektron interferencia jelenségeit a φ illetve a Φ fázisuk határozza meg, akkor miért ne játszhatna szerepet ez a két fázis, amikor az elektron és foton egymással kerül kölcsönhatásba? Ha a két fázis egyezik és emellett ΔΦ is nulla, létrejön a kölcsönhatás, ha jelentős eltérés van, akkor nem. Minden egyes detektorban elektronok vannak, az a detektor fog megszólalni, ahol az elektron fázisa a legjobban egyezik a fotonéval a kölcsönhatás pillanatában. Amikor a forrásunk emittál egy fotont, nem ismerhetjük a fázisát, úgyszintén ismeretlen előttünk, hogy a detektorokban éppen mekkora az egyes elektronok fázisa. Emiatt csak azt tudjuk megmondani, hogy az egyes detektorok mekkora valószínűséggel szólalnak meg. Ezt a valószínűséget írja le a kvantummechanika! Úgy is fogalmazhatunk, hogy nem vagyunk képesek két kísérletet úgy végrehajtani, hogy a kezdő feltételek azonosak legyenek a fázisok ismeretlensége miatt. Így a kísérletek várható eredményét úgy tudjuk megmondani, ha számba vesszük a lehetséges fázisokat egy valószínűségi faktorral és erre átlagolunk. Ez felel meg a kvantummechanika módszerének, amikor az állapotfüggvénnyel képzett integrállal meghatározza az egyes fizikai operátorok várható értékét és két állapot között annak valószínűségét, hogy az átmenet létrejön..

Kétrészecske kísérletek és a Bell-egyenlőtlenség

Másik típusú paradoxont képviselnek a kétrészecske kísérletek, melyek a kezdetben csak gondolatkísérletek voltak, de később megvalósításra kerültek. Először Aspen végzett ilyen kísérletet, de vele egyező eredményre jutottak más szerzők is. Az Aspen-kísérletben két ellentétes irányban megfigyelt részecske (például egy elektron és pozitron), vagy két foton szerepel, melyeket a kibocsátás helyétől egyenlő távolságban detektálunk. A kísérletek célja az együtt kibocsátott fotonok polarizációs irányának meghatározása. Fotonok polarizációját vizsgálva Aspen és munkatársai azt találták, hogy a két polarizációs állapot, amit egyidejűleg detektáltak éppen ellentétes. A koppenhágai iskola ezt úgy interpretálja, hogy a kibocsátás után is állandó kontaktusban maradnak a fotonok, mintegy „összefonódva” és emiatt, amikor az egyik foton felvesz egy polarizációs irányt, a másik ehhez késlekedés nélkül „igazodik”. Ez a magyarázat viszont azt jelenti, hogy a fotonok közötti információcsere sebessége meghaladja a fény sebességét! De ez csak a fotonok információcseréjét jelenti, a kísérletező erről nem tud, válaszolják erre a koppenhágai iskola követői és bevezetik az összefonódott részecskeállapotok koncepcióját, amely egyetlen egységnek tekinti a két részecskéből álló rendszert. Ez a koncepció a kölcsönhatások nem-lokális jellegének felel meg, azaz nem két pontszerű (vagy szűk térben lokalizált), hanem térben kiterjedt objektumok kölcsönhatásáról van szó. Evvel ellentétes az EPR által felvetett koncepció, amelyik a kvantummechanikában nem szereplő rejtett paraméterekkel magyarázná, hogy miért van rögzített kapcsolat a két foton polarizációja között. Ennek az elvi lehetőségnek kizárására komoly erőfeszítések történtek, legmesszebbre Bell jutott, aki egy összetett kísérletsorozat feltételezésével zárta ki a rejtett paraméterek létezését. Megállapítása szerint, ha létezne a polarizációt meghatározó rejtett paraméter, ez ütközne a kvantummechanika szabályaival, ugyanis a bizonytalansági elv miatt nem ismerhetjük teljes pontossággal a foton polarizációs irányát a képződéskor is, meg a detektáláskor is. Ez a nevezetes Bell-egyenlőtlenség. Más szerzők a rejtett paraméter koncepciót próbálják helyreállítani megkérdőjelezve Bell gondolatmenetének logikáját, amelyik egyrészt feltételezi a kölcsönhatás lokális jellegét, másrészt abból indul ki, hogy bármely gondolatkísérlet eredménye szükségszerűen egyértelmű (counterfactual definiteness).

Értelmezés a fiktív tér koncepció alapján

Vizsgáljuk meg a rejtett paraméterek problémáját az előző bejegyzésben ismertetett fiktív tér koncepció alapján. Bell gondolatmenetében van egy önkényes feltételezés, mely szerint a rejtett paraméter létezése egyet jelent az egyes részecskék abszolút polarizációjának mérhetőségével. Erre a feltételezésre azonban nincs szükség, elegendő a rejtett paramétertől annyit megkövetelni, hogy rögzítse a két részecske relatív polarizációját. A foton kibocsátásakor nem viszonyíthatjuk a polarizációs irányt a mérő műszer által kijelölt síkhoz, mert a kölcsönhatásban nem levő foton számára erről az irányról nincs információ, vagyis ebben az állapotban az irány fiktív! A két foton relatív fázisa azonban lehet rögzített, mert a megmaradási törvények miatt a két fázis ellentétes lesz, és ez megőrződik a továbbiakban is a frekvenciák azonossága miatt. Tehát nem tudjuk ugyan, hogy mi a kezdeti fázis a fotonok kibocsátásakor, de abban biztosak lehetünk, hogy a fázisok különbsége nem változik. Nincs szükség tehát elméleteket konstruálni az összefonódó fotonokról, vagy más részecskékről! Einstein a rejtett paraméterek feltételezésével arra a következtetésre jutott, hogy a kvantummechanika nem teljes, azt ki kellene bővíteni. Ilyen kibővítésre azonban nincs szükség, mert a hullámfüggvényben már szerepel egy ismeretlen fázis, amely egyértelműen meghatározza a mérés kimenetelét. A mérést végző azonban nem ismerheti ezt a fázist, vagyis a fázis határozatlan, de még is csak létezik. A fázisnak tehát többlet szerepe van annál, mint amit a szokásos kvantummechanikai interpretáció feltételez! Nem csak arról van szó, hogy a fázis a szuperpozíció elve szerint létrehozza az optikai interferenciát, hanem ezen túlmenően rögzíti a relatív polarizációt az egyidejűleg kibocsátott fotonok között. Tehát a fázis határozza meg,hogy mi lesz a kimenetele az egyedi elektronok és fotonok kölcsönhatásának.

A kezdő feltételek bizonytalansága

Térjünk még ki a counterfactual definiteness (feltételezett meghatározottság) fogalmára. Ez abból indul ki, hogy lehetséges megadni egyértelműen a kísérletek kezdő feltételeit, és ha létezik valamilyen rejtett paraméter, az már a fotonok kibocsátásakor rögzíti a polarizációs irányt. Amint már utaltunk rá, ez azért nem fogadható el, mert kölcsönhatásmentes állapotban nem beszélhetünk valódi irányokról, továbbá minden elektron és foton individuális kezdő fázissal rendelkezik, amit azonban nem ismerhetünk, és emiatt nem tudjuk a megismételt kísérletben garantálni, hogy azonosak a körülmények. Ez okozza, hogy a kísérletek eredménye is változó lehet (például az egyik foton visszaverődik az üveglapról, a másik áthalad rajta).

A Pauli elv

Az elektronok eloszlása fémes vezetőkben eltér a termikus rendszerek Boltzmann statisztikájától. A termodinamikai Boltzmann eloszlás azon alapul, hogy a részecskék, vagy molekulák megkülönböztethető tulajdonsággal rendelkeznek. A fémes vezetőkben az eloszlást Fermi statisztikának nevezzük, ami az elektronok megkülönböztethetetlenségéből következik. Ez a Pauli elvre vezethető vissza, ami kimondja, hogy nem lehet két elektron azonos kvantummechanikai állapotban. Ellentmond-e ennek, ha különböző elektronokról beszélünk az individuális fázisok miatt? Nem, mert a kvantummechanika által meghatározott fizikai mennyiségek értéke és a különböző állapotok közötti átmenetek valószínűsége már független a hullámfüggvény fázisától. A kvantummechanika ugyanis olyan elmélet, amelyik jól leírja a kísérleti eredményeket, de nem foglalkozik a kísérletek által meghatározhatatlan tulajdonságokkal, például az egyes elektronok, vagy fotonok fázisával.

A természet hierarchiája és determinizmus

Ha az elemi folyamatok determinisztikusak is, következik-e ebből, hogy a teljes fizikai determinizmus világában élünk? Véleményem szerint nem! Ha ismernénk a testemben lévő összes elektron és más részecske fázisát és összes fizikai paraméterét, vajon ebből meghatározható lenne, hogy éppen mit gondolok? Aligha. A determinizmus csak az egyszerű elemi folyamatokra érvényes, más szóval az elektronoknak nincs szabad akaratuk. Ha a fizika korlátozott szemléletmódjára (a Galilei elvekre) támaszkodunk, akkor sem vezet a részfolyamatok egyértelműsége a magasabb szervezeti formák determinizmusára. Nagyon leegyszerűsítve beszélhetünk a mozgásformák egymásba ágyazott hierarchiájáról. Kezdve a szubatomi részecskék mozgástörvényeivel, amelyre ráépül az atomok világa, majd a molekuláké, ahol a kémia írja le a változások folyamatát a szervetlen és a szerves vegyületek területén. A kémiai folyamatok felett pedig ott vannak a biológia, az élet szervezési formái. A hierarchia sajátja, hogy a sok-sok elemből felépülő struktúrák átrendeződési folyamatai csak részben vezethetők vissza az egyes elemi lépések determinisztikus szabályaira, a hierarchia minden szintjének megvannak a sajátos törvényei. Gondoljunk például arra, hogy milyen bonyolult reakciók mennek végbe a sejt osztódásakor, hogyan csavarodnak fel és le a DNS-szálak, hogyan történik a genetikai információ másolása. A folyamatok sohasem százszázalékosak, mert az egyes elektronok bizonyos fáziskombinációi a szokásostól eltérő utakat engednek meg. Ezért a fizikai és kémiai folyamatok legpontosabb ismeretében sem lehet a biológia folyamatokat és az élet eredetét egyértelműen levezetni. A genetikai kódok másolási hibái a biológia evolúciós törvényeiben jelennek meg. Az összetett folyamatok egymásra épülése egyre nagyobb szabadságot enged meg a folyamatokban, a véletlen egyre inkább teret nyer a determinizmussal szemben, és ez magasabb szinten már elvezet az emberi gondolkozás és cselekvés szabadságához, a szabad akarat megnyilvánulásához.

A szabad akarat világa

Voltaképpen arról van szó, hogy az élet és még inkább a „szellem” szintjén túl kell lépni a Galilei elveken, másfajta gondolkozásra van szükség, amiben az anyagi és szellemi világ egységet alkot. Ezért pont az ellentéte lehet igaz, annak a fizikuskörökben elterjedt felfogásnak (lásd Stephen Hawking és Roger Penrose: „A tér és az idő szerkezete”), amely a kvantumfolyamatok határozatlanságából kiindulva akarja magyarázni a szabad akaratot. Szerintem az elemi folyamatok determináltak, de ez megengedi, hogy a rendkívül összetett – az életet, az emberi tudatot és a társadalmat magában foglaló világban – színre lépjen a szabadság az elemi folyamatok szigorú determinizmusa felett.

Link a folytatáshoz: A kvantumvilág rejtélyei 3.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

Egy korábbi bejegyzésben (Determinizmus és kvantummechanika: a szabadság szintjei a fizikában) már áttekintettem a kvantummechanika néhány olyan jelenségét, aminek összehangolása szokásos fogalmainkkal nehézséget okoz és paradoxonokhoz vezet. Itt most részletesebben és szemléletes példákkal kiegészítve veszem elő ezeket a kérdéseket, elsőként a kétrészes kísérleteket, amelynek értelmezése a legvilágosabban mutatja a klasszikus fizika és a kvantumfizika eltérő szemléletmódjának okait.

Az EPR-paradoxon

A kvantummechanika értelmezési dilemmái ilyen vagy olyan módon a Heisenberg-féle bizonytalansági elvhez kapcsolódnak. Addig egyeznek az álláspontok, amíg nagyszámú részecske tulajdonságairól van szó, mert ekkor elfogadható a valószínűségekre alapozott statisztikai leírás. A kvantummechanikai korrespondencia elv szerint a határozatlansági törvények belesimulnak a makro-világban a klasszikus fizika determinizmusába. Más a helyzet, ha egyetlen foton, vagy elemi részecske tulajdonságait vizsgáljuk. Erre példa az Einstein, Podolsky és Rosen által felvetett gondolatkísérletek esete (EPR-paradoxon), melyek közül néhányat már tényleges kísérlettel is ellenőriztek.

A kétréses kísérlet

Az EPR-paradoxon talán legtöbb vitát kiváltó esetét képviselik a kétréses kísérletek. A kísérlethez monokróm fényforrást használunk, amelyik két keskeny (a hullámhosszal összemérhető) résen halad át és egy fényérzékeny ernyővel vizsgáljuk a beeső fény intenzitását. Eddig a kísérlet nem több mint a jól ismert interferencia jelenség megfigyelése: az optikai úthosszak különbsége által meghatározott helyeken fénymaximumokat és minimumokat észlelünk. A kísérlet akkor ad meglepő eredményt, ha egyesével indítjuk el a fotonokat, és külön-külön detektáljuk a felvillanásokat. Ebben az esetben ott tapasztalunk gyakrabban felvillanást, ahol interferencia maximum van és nincs felvillanás a minimum helyeken. Tehát nem az egyidejűleg kibocsátott fotonok közötti interferenciát látjuk, hanem az egyes fotonok saját magukkal lépnek interferenciába, ami arra mutat, hogy a foton egyszerre halad át mind a két résen!

Milyen információnk van a fotonról a kölcsönhatás előtt?

Ez a jelenség nem fordulhat elő a klasszikus fizikában, viszont jellemző a kvantumos állapotokra. Mi ennek az oka? Képzeljük magunkat a foton helyébe! Milyen információval rendelkezik a kölcsönhatás előtt? Olyan a helyzete, mint magunknak, ha az üres térben lennénk és semmilyen fény, semmilyen információ nem jutna el hozzánk. Ekkor nem jelentene számunkra semmit az irány fogalma. mert környezetünk nem adna számunkra semmilyen összehasonlítási lehetőséget. Emiatt a foton számára a tér fiktív! A foton terjedésérnek leírására mi mégis a szokásos térfogalmainkat használjuk, de mivel nem rendelhető semmilyen határozott irány a mozgáshoz, így azt mondjuk, hogy minden irányban egyenlő valószínűséggel terjed a fény.

A foton karakterisztikus tulajdonságai

A fotonról két dolgot azonban tudunk, egyrészt c sebességgel mozog, másrészt állapota periodikusan változik. A fénysebességű forgás modellben ez a periodikusság a forgásból származik, melynek frekvenciája határozza meg a foton energiáját is. A forgás miatt a foton minden időpillanatban egy kitüntetett fázissal rendelkezik, melynek értéke kizárólag a foton kibocsátásától számított időtől függ. De merre halad a foton, ha nincs irány? Jobbra, balra, előre vagy hátra? Ezeknek a fogalmaknak nincs értelme, ha nem beszélhetünk valódi mozgási irányról. A foton tehát minden időpillanatban tetszőleges irányban haladhat. Mozgásában kizárólag csak a fázis váltakozása játszik szerepet. Ennek felel meg a Huygens által felállított elképzelés, aki úgy értelmezte a gömbhullámokban történő terjedést, hogy minden időben és pontban a fény újabb gömbhullámot kelt és a gömbhullámok összegződése alkotja meg a terjedési képet. Ez kijelöl egy gömbhullám frontot, ameddig egyáltalán eljuthat a fény egy adott idő alatt és ez a front jól definiált fázissal rendelkezik. Mivel a foton mozgási iránya nem határozott, így a gömbön belül bármely ponthoz a foton különböző utakon is eljuthat, ezért a foton a teljes gömbben mindenütt jelen van. Tehát jelen van egyidejűleg mind a két résnél is.

Hogyan halad át a foton a réseken?

De mi történik a fotonnal, amikor eléri azt a felületet, ahol két rést alakítottunk ki? Ott ahol nincs rés sok-sok elektron van több rétegben is és a foton kölcsönhatásba kerülhet ezekkel az elektronokkal Két dolog történhet, vagy reakcióba lép valamelyik elektronnal az első rétegben, vagy tovább halad. Viszont minden ilyen „találkozás” időt vesz igénybe, így az optikai közegben a foton mozgása lelassul. Ez a jelenség okozza vízben és üvegben a fénytörést, ahol a fotonok többsége nem nyelődik el a közeg által. Ha viszont optikailag nagyon sűrű a közeg, akkor előbb-utóbb elnyelődik a foton, tehát a falon nem jut át. De azok a fotonok, amelyek néhány rétegen túljutnak esélyt kapnak, hogy átlépjenek a réseken. Még akkor is így van, ha egyetlen fotonról van szó, ezért mind a két résnél átbújik a foton. A foton ezt persze nem észleli, mert ha nem lép kölcsönhatásba egyetlen elektronnal sem, akkor a réseknél is a szokott módon, tehát gömbhullámokban terjed tovább. Ha végül eljut a fényérzékeny ernyőhöz, akkor attól függ a detektálás esélye, hogy mekkora az optikai úthosszak különbsége a két réstől számítva, ezért a detektálás gyakorisága megfelel az interferencia szabályainak.

A hullámfüggvény redukciója

A foton tehát a detektálás előtt a terjedési gömbön belül bárhol lehet, de a detektálása már csak egyetlen pontban történhet meg. Abban a pillanatban, amikor valamelyik elektronnal kölcsönhatásba lépett már nem lesz csak abban az egyetlen pontban, ahol az elektron tartózkodik. Amikor a kvantummechanika ezt a jelenséget leírja, akkor a hullámfüggvény redukciójáról beszél. A detektálás előtt a foton hullámfüggvénye az egész térrészben való előfordulást írja le, de a detektálás után már egyetlen pontra korlátozódik a foton pozíciója. Azt mondjuk ilyenkor, hogy a foton hullámtermészete megszűnik és a detektálás pillanatában már korpuszkulaként viselkedik. A hullámfüggvénynek ez a „redukciója” sok spekulációra adott már okot, sokan keresik azt a fizikai folyamatot, ami a foton, vagy az elektron állapotváltozását előidézte. Eddig a foton szempontjából vizsgáltuk a kérdést, de hasonló a történet az elektron oldaláról is, a detektáláskor az elektron állapotát leíró hullámfüggvény is „redukálódik” a kölcsönhatás bekövetkeztekor. Véleményem szerint azonban nincs egy rejtélyes fizikai folyamat sem a foton, sem az elektron hullámtermészetének megváltozása mögött, mert a változás az információban, az irány fogalmában történik, amikor a fiktívből reálissá válik. Detektáláskor ugyanis „látjuk”, hogy hová csapódott be a foton. Mégpedig azért látjuk, mert a fényérzékeny ernyőről rengeteg foton jut el hozzánk, ez valójában a „látás”. Tehát amikor a mérést kiértékeljük, akkor már nem csupán az egyetlen fotonról, amit megfigyelünk, kapjuk az információt, hanem a fotonok garmadájától. Ez a sok foton alakítja ki aztán „valós” irányképzetünket! Egyetlen fotontól nyert információról csak akkor beszélhetnénk, ha nem látnánk az egész berendezést, de akkor az egyetlen fotonról sem tudnánk semmit! Tehát ami megváltozik az nem a foton állapot redukciója, hanem az irányról alkotott fogalmunk.

Detektálhatjuk-e, hogy melyik résen halad át a foton?

Próbáljuk meglesni, hogy valóban egyidejűleg hatol-e át a foton a két résen, ezért helyezünk el egy-egy detektort mind a két rés mögött, de gondoskodjunk róla, hogy a detektorok után a foton változatlan elrendezésben érhesse el a fényérzékeny ernyőt. Azt fogjuk tapasztalni, hogy egyszerre csak az egyik detektor szólal meg. Ennek oka, hogy egyetlen foton mindig csak egyetlen elektronnal léphet kölcsönhatásba. Ebben az esetben viszont megszűnik az interferencia, azaz a fényérzékeny ernyőn egyenletes eloszlásban jelennek meg a felvillanások. Az interferencia elmaradásának oka, hogy a detektorból már megváltozott fázisú foton lép ki, és ez a fázis már véletlen módon összegződik a másik résen átjutó fotonéval.  

LINK a folytatáshoz: A kvantumvilág rejtélyei 2.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

Elvek és egyenletek

A fizikai leírásban alapvető szerepet játszanak az egyenletek.  Ezen belül is differenciálegyenletek adják meg a mechanika, a kvantummechanika, az elektrodinamika, a termodinamika alaptörvényeit a kérdés azonban, hogyan definiáljuk a különböző törvényekben szereplő fizikai mennyiségeket. Szokásos ilyenkor az egyenletekből kiindulni és azon keresztül értelmezni a bennük szereplő mennyiségeket. Ezt nevezhetjük a matematikai gondolkodásmódnak, a fizikai gondolkodásmódnak azonban inkább megfelel a fordított út, amikor bizonyos alapelveket fogalmazunk meg és ez alapján jutunk el az egyenletekig.

A mechanika fogalmai

Induljunk ki a mechanikából. Egy mozgó test impulzusát mint tömegének és sebességének szorzatát szokás definiálni, azaz egy egyenlet áll a definíció mögött. Jobb ehelyett egy elvet megfogalmazni: Az impulzus az a fizikai mennyiség, ami egy test mozgásállapotát tartja fenn. Ez a definíció megfelel Newton első törvényének: minden test megtartja egyenes vonalú, egyenletes sebességű mozgását, amíg nem hat rá külső erő. Fogalmazzuk meg az itt fellépő újabb fogalom, az erő definícióját is. Itt Newton második törvényére szokás hivatkozni, mely szerint az erő a tömeg és a gyorsulás szorzata, tehát ismét egy matematikai egyenlet. Ehelyett ismét mondjunk ki egy elvet: az erő az a fizikai mennyiség, amelyik megváltoztatja a testek mozgásállapotát. Ebből már világos az erő és az impulzus kapcsolata: az erő megtartja, az impulzus megváltoztatja a mozgási állapotot.

Lépjünk tovább és határozzuk meg az energia fogalmát. Ezt gyakran a leejtett test potenciális (helyzeti) és kinetikai (mozgási) energiájával jellemzik. Kezdetben nem mozog a test, ekkor csak helyzeti energiája van. Az esés közben felgyorsul, a pillanatnyi sebességet a Newton-egyenlet segítségével határozhatjuk meg, majd a sebesség ismeretében kapjuk meg a mozgási energiát. Eredményül azt kapjuk, hogy a helyzeti és a mozgási energia összege állandó, azaz az energia megmarad. Ez az eljárás szintén a matematikai egyenletekre támaszkodva jut el az energia megmaradás törvényéhez. Az energia definíciója azonban épp a fordított gondolatmenetet kívánja meg: nem az energia megmaradásáról kell beszélni, hanem az energia az a fizikai mennyiség, amelyik a változó mozgásokban is megmarad. Épp ebben különbözik az impulzustól, amelyik csak az állandó sebességű mozgásoknál nem változik meg. Úgy is mondhatjuk, hogy az energia az állandóság a változásban.

Forgások és az impulzusnyomaték

Amit tehát a fizikában – és nem csak a fizikában, hanem más területeken is – vizsgálnunk kell, hogy mi az ami állandó, ami megmarad, és mi az ami változik, vagy változtat. De maradjunk a fizika területén és térjünk át a forgásokra. Ennek szemléltetésére gondoljunk a jégtáncosra, amikor a piruett figurát hajtja végre. Először széttárja a karját, majd kezével és egyik lábával a jégre rúgva lendületet vesz, amitől lassú forgásba kezd. Ezután kezeit szorosan a testéhez szorítja, amitől forgása felgyorsul. Vessük fel a kérdést: mi az a fizikai mennyiség, ami a forgás során állandó marad? Erre a válasz az impulzusnyomaték (impulzusmomentum). Tehát nem egy matematika formulával jutunk el a fogalomhoz, ami ez esetben az impulzus és a forgási sugár vektoriális szorzatával adható meg, hanem fordítva, ismét egy elv a kiindulási alap. Itt a matematikai definícióhoz azt is hozzá kell tenni, hogy a térben kiterjedt test esetén elemi pontokra kell felbontani a testet, minden egyes pontban meg kell adni az impulzust mint a kerületi sebesség és a ponthoz tartozó tömeg szorzatát, majd ezt kell szorozni a forgástengelytől való távolsággal és ezután az összes pontra összegezni (integrálni) kell. A helyes fizikai definícióban először az elvet kell megadni, majd ebből kell származtatni a matematikai eljárást és nem fordítva: megadni először a matematikai eljárást és ebből kimutatni, hogy a matematikai módszerrel adott definícióból már következik, hogy az így definiált mennyiség tényleg állandó a forgás során.

Az elemi részecskék spinje

Ha egy test impulzusnyomatékkal rendelkezik, akkor forog és véges kiterjedéssel (sugárral) rendelkezik. A részecskefizika általánosan elfogadott modellje (Standard Modell) szerint minden valóban eleminek tekinthető részecske rendelkezik impulzusnyomatékkal, azaz spinnel, ahol is a spin a redukált Planck állandó, azaz ℏ együtthatója. A fény elemi részecskéje, azaz a foton esetén a spin S = 1, míg az elektroné, protoné, neutroné ½. A fotonok energiája és frekvenciája a hosszúhullámú rádiófrekvenciás hullámoktól a gamma sugárzásig akár húsz nagyságrenddel is változhat, impulzusnyomatékuk, azaz spinjük mégis hajszálpontosan egyezik. Az S = ½ spinű (fermion) elemi részecskék tömege is különbözhet négy nagyságrenddel, lehetnek töltöttek és semlegesek is, viszont spinjük mégis azonos. A fizikai tankönyvek nem tárgyalják, hogy milyen fizikai jelenség okozza az impulzusnyomatékok egyezését, sőt arról sem írnak, hogy forognának-e ezek a részecskék, az elektron esetén pedig egyenesen pontszerűségről beszélnek. Tehát nem teljesülnek azok a kritériumok, amit minden impulzusnyomatékkal rendelkező fizikai objektumtól elvárnánk. Olyan állításokat is találhatunk, hogy a spin a részecskék saját (intrinsic) tulajdonsága, amihez nem köthető semmilyen klasszikus forgási kép, mert ezt a relativitáselmélet nem teszi lehetővé. Nézzük hát meg, hogy igaz-e az utóbbi állítás!

A speciális relativitáselmélet

A relativitás, pontosabban a speciális relativitás elméletét is valamilyen alapvető fizikai elvre lehet visszavezetni.  Ez az elv a fénysebesség állandóságának elve, ebből már a szokásos matematikai szabályok levezethetők. De miért állandó a fénysebesség és ez valójában mit jelent? Ezt abból következik, hogy az univerzumban minden kölcsönhatás véges sebességgel terjed, tehát nem csak az elektromágneses, hanem a gravitációs kölcsönhatás is. De miért létezik ez a határsebesség, ami nem léphető át semmilyen kölcsönhatásban és semmilyen fizikai objektum által? Ezt magyarázhatjuk egyrészt az univerzum végességével, mert ha az univerzum véges, akkor annak minden objektuma és minden tulajdonsága is véges. Ha végtelen lehetne a sebesség, akkor ezáltal végtelen távolságba juthatnánk egy szempillantás alatt. Másrészt a kölcsönhatások véges sebessége még akkor is szükségszerű, ha végtelen kiterjedésű lenne az univerzum. Képzeljük csak el, mi történne, ha például az egyik csillagrendszerből késleltetés nélkül érkezne meg valamilyen hatás a másikba? Ekkor a válasz is késleltetés nélkül jönne, majd hasonlóan a viszont válaszok végtelen sora. Ekkor a teljes hatás egy végtelen tagból álló mértani sorozat összege lenne, amelynek kvóciense, ha egynél nagyobb, akkor az univerzum felrobbanna, ha kisebb, akkor eltűnne. Viszont tudjuk, hogy az univerzum már milliárd évek óta létezik. Tehát a létezés maga megköveteli, hogy minden kölcsönhatásnak legyen véges határsebessége, ami nem más mint a fény sebessége vákuumban. De miért jelent a végesség egyúttal állandóságot is? Képzeljük el, hogy egy mozgó objektumból bocsátunk ki fényt. Szokásosan azt gondolnánk, hogy ekkor az objektum sebessége és a fényé összeadódik. De ha összeadódna, akkor átléphetnénk a határsebességet. Tehát ha van határsebesség, akkor nem adódhat össze az objektum és a fény sebessége. Ha viszont nem adódik össze, akkor nem is vonódhat ki. Ezért a fény kizárólag a határsebességgel mozoghat, amit szokásosan c-vel jelölünk. Ennek csak látszólag mond ellent, hogy vízben vagy üvegben a fény lassabban terjed. A lassabb terjedést a fotonok és a töltött részecskék kölcsönhatása okozza. Minden egyes „találkozáskor” a fény vagy elnyelődik, vagy tovább halad, de az utóbbi esetben a kölcsönhatás késleltetést idéz elő. És minél többször lép kölcsönhatásba a fény és az elektronok, annál lassabb lesz a terjedés sebessége.

A Lorentz kontrakció és a relativisztikus tömegnövekedés

A sebességet a megtett út és az idő hányadosa adja, ezért ha a sebesség nem adódik össze a szokott módon, akkor ez a megtett hosszakra is igaz. Következésképp a megtett út rövidebbnek látszik. Minden távolságot valamilyen fizikai objektum hosszához viszonyítjuk, ezért a tárgyak hossza is rövidülni fog. Ezt nevezi a relativitáselmélet Lorentz kontrakciónak.  A hétköznapi életben megszokott sebességeknél ez azonban elhanyagolható mértékű, viszont jelentős lesz, ha közeledünk a fény sebességéhez. A fénysebesség pedig egy olyan elvi határ, ahol már a c sebességgel mozgó objektum mérete nullára zsugorodik.  Képzeljük el, hogy egy méterrudat tartok vízszintesen az vonat ablaka előtt párhuzamosan a vonat haladási irányával. Ekkor ez „kintről”, tehát a sínek mellett, rövidebbnek látszik. De ez fordítva is igaz, ha kint tart valaki a kezében egy méterrudat, azt én látom rövidebbnek. Ebben nyilvánul meg a relativitás: a testek mérete nem abszolút, hanem attól függ, hogy a testtel együtt haladó rendszerből (vonatból) nézzük, vagy kívülről. Ha viszont valaki kint eldob egy súlygolyót párhuzamosan a vonat haladási irányával, akkor a dobást kisebbnek látjuk, ami a dinamika szerint akkor lehet, ha megnövekszik a súlygolyó tömege. Ha viszont a vonatunk képes lenne fénysebességgel mozogni, akkor a „kinti” méterrúd hossza nulla lenne, a súlygolyó tömege pedig végtelen nagyra nőne. Viszont a külső megfigyelő számára ez úgy jelentkezne, hogy nullahosszúságúnak látná a szerelvényt, és végtelennek tartaná a tömegét. Ez a végesség kritériuma miatt nem lehetséges, azaz a „vonat” nem érheti el a fény sebességét. Ez vonatkozik valamennyi tömeggel rendelkező fizikai objektumra is: sebességük nem érheti el a határsebességet.

A fény különös természete és a tömeg keletkezése

Létezik azonban egy olyan fizikai objektum, amelyik a határsebességgel mozog, ez a fény, illetve annak kvantuma a foton. Ez az előbbiek szerint úgy lehetséges, ha nulla tömeggel rendelkezik, azaz nincs nyugalmi tömege. Viszont a relativitáselmélet legfontosabb felismerése, hogy a tömeg és az energia ekvivalens, amit az E = m.c² összefüggéssel lehet kifejezni. A foton viszont rendelkezik energiával, amely arányos a rezgési frekvenciával (ν illetve ω = 2π.ν) az E = h.ν = ℏ.ω összefüggés szerint. Tehát az ekvivalencia elv szerint a foton mégis rendelkezik tömeggel! Hogyan lehetséges ez, hiszen az imént még azt jelentettük ki, hogy a fotonnak nincs tömege! Az ellentmondás úgy oldható fel, ha kétféle tömegről beszélünk, az egyik a nyugalmi a másik a mozgási tömeg. A foton nyugalmi tömege határértékben nulla, miként 1/X, ha X minden számnál nagyobb, azaz végtelen. Ekkor bár 1/X minden határnál kisebb szám, de ha szorozzuk X-szel, azaz képezzük az X*(1/X) szorzatot, mégis az egységet, tehát véges értéket kapunk. Legyen hát a fénysebességű mozgáshoz tartozó tömegnövekedési tényező az X szám és 1/X a foton nullához végtelenül közeli nyugalmi tömege, ekkor érthetővé válik, hogyan lehet a foton tömege egyrészt nulla, másrészt véges mennyiség. Evvel eljutottunk a relativitáselmélet másik alapvető fontosságú elvéhez: a fénysebességű mozgás anyagot (tömeget) hoz létre. Ez az elv egyébként kiolvasható a tömeg és energia ekvivalenciájának képletéből is: E = m.c², ahol a tömeget létrehozó fénysebesség négyzete hozza létre a kapcsolatot a tömeg és az energia között! A fotonnak azonban impulzusa is van, ami a már említett elv szerint fenntartja a fénysebességű mozgást. Az elektrodinamika szerint a foton p impulzusa arányos az energiával az E = p.c összefüggés szerint. Az arányosság következik a fénysebességű mozgás elvéből is, hiszen ekkor p = m.c az impulzus, amit c-vel szorozva kapjuk az m.c² energiát.

A foton impulzusnyomatéka

A fotonnak azonban impulzusnyomatéka, azaz spinje is van. Tehát a fotonnak a haladó mozgás mellett valamilyen forgást is kell végeznie. Adjunk ezért új értelmezést a foton energiáját és időbeli hullámait jellemző  ω körfrekvenciának és azonosítsuk ezt a forgás szögsebességével. Ha a forgás r sugarú kört hoz létre, akkor ennek kerületi sebessége u = r. ω lesz. Az r sugár nagyságának azonban határt szab, hogy az u sebesség nem lehet nagyobb, mint a c fénysebesség. A foton viszont fénysebességgel terjed, ezért bármilyen egyéb mozgással összekapcsolva is változatlan lesz az eredő sebesség, tehát a forgás kerületi sebessége is c lesz. Emiatt viszont az ω szögsebesség meghatározza a kör sugarának értékét is, azaz r = c/ω lesz. Ez a sugár pedig megegyezik a fény hullámhosszával! Az I-vel jelölt impulzusnyomatékot a mechanika úgy számítja ki, hogy szorozza a test impulzusát a forgási sugárral: I = p.r = m.c.r. Felhasználva két elvet: a tömeg és energia ekvivalenciáját: m = ℏ.ω /c² és a fénysebességű forgásét: r = c/ω, majd az m tömeg és az r sugarat behelyettesítve azt kapjuk, hogy az impulzusnyomaték I = ℏ, azaz a foton spin S = 1. Az impulzusnyomaték tehát nem függ az szögsebességtől és így érhetővé válik, hogy miért azonos a foton impulzusnyomatéka bármekkora is legyen az energiája.

A fénysebesség mint univerzális állandó

De vessük fel a kérdést, hogy mi az, ami a fénysebességű mozgásokat végzi és ezáltal anyagot, tehát tömeget hoz létre? A kérdéshez először a mozgás fogalmát kell megérteni. A mozgás a tér és az idő kapcsolata, ami matematikailag úgy fejezhető ki, hogy a tér egyes pontjait az idő mint változó függvényeként írjuk fel. Ennek a kapcsolatnak az univerzális – tehát a leíráshoz választott rendszertől független – formája, amikor fénysebességű mozgás jön létre. A fénysebességű mozgás ugyanis az egyetlen abszolút kapcsolat a tér és az idő között. Minden sebesség relatív, mert nincs az univerzumnak olyan centruma, amihez viszonyítva a testek mozgási sebességét egyértelműen megadhatnánk. Ha a vonaton átmegyünk az egyik szerelvényből a másikba, akkor beszélhetünk a vonathoz képesti sebességről, de meghatározhatjuk a sebességet a külső környezethez is. De ez sem abszolút sebesség, mert a Föld forog a tengelye és kering a Nap körül, tehát választhatnánk a Napot, amihez viszonyítjuk a mozgásunk sebességét. De ez sem abszolút, mert a Nap is kering a Tejútrendszerben, sőt ennek centruma sem abszolút vonatkoztatási rendszer, mert a Tejút is változtatja helyét a többi galaxishoz képest. Ugyanakkor bármilyen mozgást is végezzen egy fizikai objektum az általa kibocsátott fény sebessége mindig azonos lesz. A fénysebességű mozgások tehát univerzális kapcsolatot hoznak létre a tér és az idő között. A tér pontjai, melyeket egyébként csak matematikai absztrakciónak tekintünk, a fénysebességű mozgás által anyagi valóságra, azaz tömegre tesznek szert. Ezek lesznek a részecskék! Eddig csak a fotonnal foglalkoztunk, amit tehát egy forgó és egy haladó mozgás kombinációjával írunk le, de most terjesszük ki ezt az elvet valamennyi elemi részecskére!

Az elektron és a kettősforgások

Az S = ½ spinű elemi részecskék (fermionok) nyugalmi tömeggel rendelkeznek. Hogyan jön létre ez a tömeg?  Kézenfekvő a feltevés, hogy a fotonok mozgási tömegéhez hasonlóan fénysebességű mozgásokból. Fénysebességű haladás viszont nem jöhet szóba, tehát csak fénysebességű forgások hozhatják létre a nyugalmi tömeget. A foton pozíciójához nem rendelhető a tér egy kijelölt pontja, más a helyzet a fermionokkal, amihez minden pillanatban rendelhetünk egy tartózkodási helyet. Ez egyébként a kvantummechanika bizonytalansági elvéből is következik: a foton pontos impulzussal rendelkezik, ezért határozatlan a pozíciója, a fermionoknak rögzíthető a helyzete, de ez impulzusának bizonytalansága alapján történhet meg. A pozíció kijelölése az által valósulhat meg, ha két egymásra merőleges forgás kapcsolódik össze, ami létrehoz egy gömbfelületet. Nevezhetjük ezt a kettősforgást gömbforgásnak is. A két összekapcsolt forgás egymáshoz képest kétféle sodrásiránnyal rendelkezhet, az egyiket nevezhetjük jobb- a másikat balsodrásúnak. Ez a háromdimenziós tér sajátsága, amiben kijelölhetjük az egymásra merőleges x, y és z tengelyeket akár a jobb, akár a balkéz irányaival is. Ez a két rendszer nem forgatható egymásba, de egymásnak tükörképe. Ezt a tükrözési szimmetriát nevezzük kiralitásnak. Ez a kép mindjárt magyarázatot ad arra, hogy miért létezik világunkban anyag és antianyag: az egyik lehet a jobb- a másik a balsodrású kiralitás. A másodlagos forgások ellentétes perdülete kiolthatja egymást létrehozva az egytengelyű forgást. Ez felel meg annak, amikor az anyag és antianyag annihilál és gammasugárzást hoz létre.

Mit jelent az elektron pontszerűsége?

A részecskefizika az elektront pontszerűnek tekinti, amit kísérletileg a Bhabha szórás támaszt alá: amikor az elektronokat pozitronokkal bombázzák. Ekkor olyan szórási képet kapunk, mintha a töltések egyetlen matematikai pontba sűrűsödnének össze. A pontszerűség elve viszont ellent mond annak, hogy az elektronnak van impulzus és mágneses nyomatéka is. A látszólagos ellentmondás azonban feloldható fénysebességű forgások esetén. Az r sugarú kör kerülete 2r.π, az r sugarú gömbbé 4r². π. A mozgás irányában azonban a távolság lecsökken a Lorentz kontrakció szerint, ami fénysebességű mozgásnál nulla lesz. De ez csak a mozgás irányában érvényes, arra merőlegesen nem változik a távolság. Mivel a sugár merőleges a körforgás irányára így annak ellenére, hogy a kerület, illetve gömbforgásnál a felület nullára csökken, a sugár változatlan marad. A felület eltűnése miatt így a Bhabha szóráskísérletben azt várjuk, hogy a hatáskeresztmetszet nulla lesz, míg a sugár nem változik létrehozva az impulzus és a mágneses nyomatékot.

Mekkora az elektron spin?

A kettősforgás arra is magyarázatot ad, hogy miért éppen fele a fermionok impulzusnyomatéka a fotonhoz képest. Mivel két független forgás alkotja a részecskét, így a forgás fenntartásához elegendő fele akkora impulzusnyomaték is. Minden forgás azonban létrehoz egy kifele mutató centrifugális erőt, ezt érezzük a körhintában is, de ez hat a Földre is a keringő mozgás miatt. Hasonlóan beszélhetünk kifelé húzó erőről az atomban is az elektronok mozgása miatt. A forgás fenntartásához szükség van egy ellenerőre, amit centripetális erőnek nevezünk. Ennek iránya pont ellentétes a centrifugális erővel és azt kompenzálni tudja. Ez a centripetális erő a körhintában a székeket a tengelyhez rögzítő kényszerhatás, a Föld keringésénél a gravitációs erő, az atomban a negatív töltésű elektronok és a pozitív töltésű atommagok közötti elektromos vonzás. Fölmerül a kérdés, hogy ha az elemi részecskéket a fénysebességű forgás hozza létre, akkor milyen erő egyenlítheti ki a centrifugális erőt?

Gravitáció: az általános relativitáselmélet

A magyarázat megtalálásához a fizika egy újabb fejezetét kell megnyitni, a gravitáció eredetét magyarázó általános relativitáselméletet. Ennek alapelve, hogy a gravitáció a tér görbületétől származik és ezt a görbületet a tömeg hozza létre. A háromdimenziós tér görbületét nehéz elképzelni, ezért gondoljunk ezért egy síkra, például egy gumimatrac felületére. Helyezzünk rá apró gyöngyöket, majd egy nehéz súlygolyót, ami a matracot belapítja. Ekkor a bemélyedés irányában a gyöngyök odagurulnak a mélyedésbe. Ha nagyobb súly helyezünk oda, akkor a gyöngyök gyorsabban és nagyobb távolságból fognak odagurulni. Ebben a képben a kétdimenziós vízszintes sík a mélységi, tehát a harmadik dimenzió irányában görbül be. Háromdimenziós tér esetén viszont a kiegészítő dimenzió már a negyedik lesz, ami a Minkowski által bevezetett négydimenziós téridőben képzelhető el azáltal, hogy a háromdimenziós tér az idő irányában görbülhet meg. Ennek a görbületnek két típusa lehet, az egyik felel meg az általános relativitáselmélet szokásos makroszkopikus térszerkezetének, a másik pedig az elemi részecskéket alkotó mikroszkopikus torzulás. Foglalkozzunk először az előbbivel, mert ez hozza létre a szokásos gravitációs vonzást. Itt most megmutatom, hogy ez a görbület visszavezethető a speciális relativitáselméletre.

A bolygómozgás Kepler törvényei

Induljunk ki a bolygómozgás Kepler törvényeiből. A további gondolatmenet nem kíván ugyan matematikailag nehezen áttekinthető lépéseket, mégis inkább a blog korábbi bejegyzésére utalok (Térgörbület és gravitáció forgó rendszerekben) , mert célom az elvek kiemelése, ami háttérbe szorulhatna a matematikai levezetések során. Kepler a csillagászati megfigyeléseket felhasználva kapcsolatot állapított meg a bolygók Naptól való átlagos távolsága és a keringési idő között: minél távolabb van egy bolygó a Naptól, annál hosszabb idő alatt tesz meg egy teljes fordulatot. Ezt a szabályt magyarázta meg Newton, amikor felírta a gravitációs törvényt, mely szerint két tömeg között akkora vonzó erő jön létre, ami arányos a tömegekkel, de ereje csökken a távolsággal. Ezt a törvényt kívánom magyarázni a speciális relativitáselméletből ismert Lorentz kontrakció segítségével.

Lorentz kontrakció és a gravitáció Newton törvénye

A bolygó keringése során a teljes pálya hossza kissé megrövidül a Lorentz kontrakció miatt, aminek mértéke keringés sebességétől függ a fénysebességhez viszonyítva. A keringő mozgás sajátossága, hogy ha kicsi a bolygó tömege a Naphoz képest, akkor a pálya független a bolygó tömegétől, csak a Nap tömege és a Naptól való távolság számít. Ebből következik, hogy a határértékben nullatömegű térpontok is ugyanolyan pályán mozoghatnak a Nap körül, mint az egyes bolygók. Más szóval maga a tér végezhet körforgást bármely tömeggel rendelkező objektumok körül. A Lorentz kontrakció miatt a pálya hossza rövidülni fog, tehát nem az euklideszi geometriában megszokott 2r.π határozza meg a kör kerületét, hanem ennél kisebb lesz, amit úgy írhatunk le, hogy a valódi sugár helyett egy kisebb „kerületi”, vagy „relativisztikus” sugárról beszélünk. Ezt a rövidebb sugarat hasonlítsuk össze a valódi, azaz a keringő testnek a centrumtól való távolságát mérő sugárral ,és a két sugár arányával jellemezzük a tér görbületét. Ha nincs rövidülés, azaz a két sugár hossza azonos, akkor a tér nem torzul. Ellenkező esetben viszont ez a torzulási arány határozza meg a gravitációs erőt. Ebből a felfogásból indulva eljuthatunk a gravitáció Newton törvényéhez.

Erős gravitáció: a részecskék forgását fenntartó erő

Ezen a sikeren felbátorodva, most nézzük meg, hogy mekkora erőt kapunk, ha a fénysebességű mozgás miatt a pálya kerülete nullára csökken, azaz a két sugár aránya nulla lesz!  Ezt tekintjük extrém mértékű mikroszkopikus torzulásnak. Mivel a mechanika elvei szerint az erő a potenciális energia térbeli változására vezethető vissza, ezért azt vizsgáljuk, hogy egy adott frekvenciával és a hozzá tartozó m mozgási tömeggel rendelkező részecskének mekkora lesz a potenciális energiája, ha a torzulás extrém mértékű a fénysebességű forgás miatt! Az itt nem közölt, de a korábbi bejegyzésben bemutatott számítás szerint a potenciális energia –m.c² lesz! Tehát pontosan megegyezik az m.c² nyugalmi energiával! Ez a nyugalmi energia azonban éppen hogy nem „nyugalmi”, hiszen fénysebességű forgástól származik és megfelel a forgás kinetikus energiájának. (Itt meg kell jegyezni, hogy a nem relativisztikus mechanikában a kinetikus energia kifejezésében szerepel az ½ együttható, de ez a formula csak kis sebességeknél érvényes, a fénysebességű mozgásnál az ½ együttható már elmarad).

A potenciális energia tehát pontosan kiegyenlíti a mozgási energiát, és ebből származtathatjuk a centrifugális és centripetális erőket, amelyek ellentétes irányban hatnak és kompenzálják egymást. Ezt a részecske forgást stabilizáló erőt nevezem erős gravitációnak. A fénysebességű elemi forgások tehát extrém mértékű, de rendkívül parányi kiterjedésű mikro-torzulásokat (tüskéket) hoznak létre a tér szerkezetében. Ezek a parányi torzulások viszont maguk körül lankás –  de nagy távolságba ható – torzulásokat hoznak létre, melyek összegződnek és a hatalmas számú részecske révén létrehozzák a szokásos gravitációs teret.

A forgásmodell kapcsolata a húrelmélettel

Az előzőek szerint a nyugalmi tömeggel rendelkező részecskéket két fénysebességű forgás hozza létre, melyek felülete nulla kiterjedésű, de mégis véges a sugaruk, tehát két dimenzió elvesztése miatt valójában egydimenziós alakzatok. Ebből a szempontból hasonló szerepet játszanak mint napjain fizikájában a húrok, szuperhúrok, bránok, vagy M-alakzatok és még sorolhatnám a divatos elméletek sorát. Az egydimenziós húrok rezgési frekvenciája határozza meg a részecskék tömegét és minél rövidebb a húr, annál nagyobb a tömeg, illetve az energia. Az említett elméletek viszont a szokásos négydimenziós teret további dimenziókkal egészítik ki, melyeket semmilyen kísérleti tapasztalat nem támaszt alá, ráadásul a modellek nem értelmezik az anyag és antianyag kettősségét, nem magyarázzák a spin eredetét és az elektromos töltést sem. Az általam javasolt kép épp fordított irányban ad magyarázatot a részecskék szerkezetére, mert a forgó gömb sugara nem a négydimenziós téridőt kiegészítő további dimenzió, hanem ellenkezőleg a három térbeli dimenzió egyre való redukciója a fénysebességű mozgás miatt.

A mozgás két arca: térgörbület és fénysebességű forgások

A fénysebességű forgás és a tér extrém mikroszkopikus torzulása ugyanannak a jelenségnek a kétféle megközelítése. Mert mi az a mozgás? A tér és az idő dimenziójának összekapcsolása. Ha forgásról beszélünk, akkor a térkoordináták függését vizsgáljuk az idővel kifejezve, ha a forgások által előidézett tértorzulást tárgyaljuk, akkor megfordítjuk a képet és az idő mértékét keressük a tér különböző helyein. Az általános relativitáselmélet szerint más tempóban száguld az idő (az óra lassabban jár) az erős gravitációs terekben, ez az idő dilatáció jelensége. A foton nem is érzékeli az időt, számára a milliárd éves út megtétele egy másik galaxisból csupán egyetlen pillanat. A részecske forgások kerületi sebessége, azaz a c, a nullahosszúságú kerület és a nulla idő aránya. A matematikai analízis szerint  két nullához végtelenül közeli mennyiség aránya lehet véges, ezt nem más mint a differenciálhányados. A sebességet is úgy számítjuk ki, hogy meghatározzuk az arányt a végtelenül rövidnek tekintett út és a végtelen rövid idő között. A matematikai fogalmak fontosak a fizikai törvények megértéséhez, akkor is, ha nem az egyenleteket tekintjük a fizikai elvek alapjának, hanem fordítva a fizikai elvek irányából közeledünk a matematikai egyenletek felé.

Az elektromágnesesség és a Coriolis erő

A modern fizika az elektromosan töltött részecskék közötti kölcsönhatást is kvantumos jelenségként kezeli. Ennek elve, hogy a töltések virtuális, azaz kísérletileg megfigyelhetetlen fotonokat bocsátanak ki és nyelnek el és ezek a fotonok hozzák létre a töltések közötti elektromos kölcsönhatást. Ez az un.  kvantum térelmélet. Az elmélet jól értelmezhetjük, ha a részecskék fénysebességű forgásaiból indulunk ki. A forgások során a már említett centrifugális erőn kívül megjelenik a Coriolis csavaró erő is, ha a forgó rendszeren belül valamilyen objektum mozgást végez. Ennek jól ismert példája, amikor a Föld forgása összekapcsolódik a sarkoktól az egyenlítő irányába történő légköri mozgással vagy tengeráramlással. Ez a Coriolis erő az áramlást megcsavarja és örvényeket, körbefutó áramlatokat hoz létre. Az áramlatok sodrásiránya ellentétes a Föld északi és a déli féltekéjén. Ennek oka, hogy a két esetben ellentétes a forgáshoz viszonyítva az áramlási irány. Hasonló a helyzet a részecskék kettős forgásánál, ahol az egyik forgás a Coriolis hatáson keresztül megcsavarja a másikat. A két eredeti forgás királis szimmetriája szabja meg, hogy milyen lesz a csavarodás körbefutási iránya. A Coriolis erő ily módon egytengelyű forgásokat indukál, ami értelmezésünk szerint nem más mint a foton. A Coriolis erő nagysága a mozgások sebességétől függ, és mivel a sebesség valamennyi részecskénél a fénysebesség, így a kölcsönhatás nem függ a tömegtől és valamennyi töltött részecskénél azonos. Evvel magyarázzuk, hogy az elemi töltés miért azonos valamennyi megfigyelhető elemi részecske esetében. A proton, neutront és hasonló összetett részecskéket alkotó, de kísérletileg megfigyelhetetlen kvarkok kivételt képeznek, mert az elektronhoz képest törttöltéssel rendelkeznek. Ennek oka a kvantummechanikai szuperpozíciós elv, aminek értelmezésével más bejegyzésben foglalkoztunk.

A kölcsönhatások mezőelmélete

A mikrovilág fizikai törvényei kvantumos alakban jelennek meg, emiatt alakult ki a fizikusokban az a meggyőződés, hogy minden kölcsönhatás, minden erő csak kvantumos lehet. Ezen az alapon próbálták meg kidolgozni az egységes mezőelméletet. (Elterjedtebb, de félreérthető térelmélet elnevezés). A mezőelméletben az elektromágneses kölcsönhatást a virtuális fotonok közvetítik, sikerült közvetítő részecskét definiálni az atommagokat  és azok alkotóit, a nukleonokat, valamint a kvarkokat összekötő erős kölcsönhatásra, amit gluonnak neveztek el, úgyszintén felfedezték a részecskéket egymásba alakító gyenge kölcsönhatás közvetítőit is, nem sikerült azonban az egységes mezőelméletbe bevonni a gravitációt. . Ennek oka, hogy nem a kvantumokra kell visszavezetni a gravitációt, hanem fordítva a gravitációs erő alapján lehet értelmezni a kvantumot. Ilyen alapon jutottam el a részecskék fénysebességű forgásaira alapozott részecskemodellhez, amelyben nem csak az elektromágneses kölcsönhatást, hanem az erős és gyenge kölcsönhatást is értelmezni lehet, de erre itt nem térek ki, helyette korábbi bejegyzésekre utalok (Az elektro-gyenge kölcsönhatás és az elemi részecskék átalakulása, Barangolás a kvarkok és elemi részecskék világában, A Dirac egyenlettől az általános fermion egyenletig). Az általam felépített fizikai modellben minden kölcsönhatás azáltal jön létre a fizikai objektumok között, hogy az elemi, kéttengelyű forgások, azaz a részecskék megváltoztatják a környező teret, abban másodlagos forgásokat hoznak létre. Ennek egyik formája, amikor egytengelyű fénysebességű forgások, azaz fotonok lépnek ki és nyelődnek el. Ennek felelnek meg a kvantum térelméletben a virtuális fotonok. 

A részecske környezetének másik perturbációja a gravitációs erő, amely, bár a távolság függvényében azonosan csökken, mint az elektromágneses kölcsönhatás mégis alapvetően eltér abban a tekintetben, hogy függ a részecskék tömegétől. Úgy is fogalmazhatunk, hogy a gravitációs vonzás a részecskék forgási frekvenciájától, míg az elektromágneses a forgás kerületi sebességétől függ. Mivel ez utóbbi mindig a fénysebesség, ezért az elektromos töltés, ami a kölcsönhatás hordozója minden részecskében azonos, de előjele függ a részecske királis szimmetriájától. A kétféle előjel avval magyarázható, hogy a kiralitás determinálja a kibocsátott és elnyelt fotonok forgásának polarizációs irányát. Az előbbiek értelmében a két távolba ható kölcsönhatás úgy fogható fel, hogy az elemi forgások hatása túlterjed a részecskék saját sugarán, más szóval az elemi forgás megváltoztatja a környező teret. Mi határozza meg ennek mértékét? Erre jelenleg nem ad választ a fizika, ez úgy tekinthető mint egy „csatolás” a részecske és a környezete között, ami a tér valamilyen belső sajátsága. A csatolás mértékét az elektromágneses kölcsönhatásban a Sommerfeld-féle állandó (1/137), a gravitációét a gravitációs állandó határozza meg.

Fölvetődik a kérdés, hogy miért nem lehetett a gravitáció kvantumelméletét kidolgozni? Azért, mert ennek a kölcsönhatásnak nincs kvantuma. Miért? Mert a kvantum az elemi forgáshoz tartozó impulzusmomentum, azaz a spin. Az elemi forgás pedig fénysebességű forgást jelent. A gravitáció esetén lassú és a távolság függvényében csökkenő frekvenciájú forgások jönnek létre a gyorsan forgó részecskék körül. Minél nagyobb frekvenciájú a részecske forgása, annál erősebben változtatja meg a mozgás a környező teret. Mivel ez a lassú forgás nem éri el a fénysebességet, így nem járul hozzá tömeg és impulzusmomentum. Ha pedig nincs spin, akkor kvantum se lehet, mert minden kvantum a spinhez kapcsolódik.

Az egységes fizikai világkép: a téridőrészecske

A világ egységes, amit egységes fizikai világképpel írhatunk le. Ennek fontos lépését tette meg Minkowski, amikor bevezette a téridő fogalmát. A tér nem lehet meg idő nélkül, ami fordítva is igaz. A két fogalom áthatja egymást, aminek egyik megfogalmazását adja meg a speciális, a másikat az általános relativitáselmélet. Innen lépünk eggyel tovább, amikor a részecskéket is bevonjuk a fogalomkörbe, mert a részecskék nem külön létezők a téridőben, hanem a téridő speciális megnyilvánulásai a mozgásokon keresztül. Definiálhatjuk a részecskéket a tér elemi, azaz fénysebességű forgásaival, de értelmezhetjük a tér mikroszkopikus görbületei által is. A két értelmezés ekvivalens. A tér viszont azáltal válik leírhatóvá, hogy léteznek benne az elemi forgások, amelyek egymással kölcsönhatásba lépnek és ezáltal értelmet adnak a távolság és az irány fogalmának is. Részecskék nélkül nincs értelme térről beszélni. Ugyanez elmondható az idő és a részecskék kapcsolatáról is. Az idő úgy jelenik meg, ha a részecskék egymáshoz való viszonyát és átalakulásait sorba rendezzük és megkülönböztetjük egymástól az okot és az okozatot és ennek vég eredményeképpen kibontjuk a fizikai idő fogalmát. Az egységes fizikai világkép alapját egyetlen fogalommal a téridőrészecskével adhatjuk meg. Evvel kifejezzük, hogy nincs tér és idő részecskék nélkül, és nincs részecske téridő, azaz mozgások nélkül.

Az ősrobbanás mint fénysebességű kaotikus mozgás

Alkalmazzuk ezt a szemléletet az ősrobbanás elméletében is. Az elmélet kiindulópontja a táguló univerzum, ami a távoli galaktikák vörös eltolódásából következik. Az elmélet másik sarokpontja, a mikrohullámú háttérsugárzás jelensége. Az elmélet szerint az ősrobbanás korai szakaszában először az elemi részecskék alakultak ki, majd ezek összekapcsolódása hozta létre az atommagot, majd az atomokat és később jöttek része az összetettebb objektumok és a csillagok. Ezt megelőzően a kvarkok és gluonok plazmáját tételezik fel. Ez a feltevés szerintem nem állja meg a helyét, mert kvarkokat csak a hadron típusú részecskék (ide tartozik a proton és neutron is) összetevőiként lehet megfigyelni, ezért nem indokolt, hogy létezésük megelőzze az őket stabilizáló formációk keletkezését. A fénysebességű modellből az következik, hogy a kezdeti ősállapot fénysebességű, pulzáló mozgásokból állt, ezek kaotikus mozgások voltak, melyben a gyors ütközések megakadályozták a forgási állapotok kialakulását. Az univerzumnak ebben a korai korszakában tehát nem voltak elemi forgások, így a kvantum sem létezett, ez volt az univerzum kvantum előtti állapota.

 Minél nehezebb egy részecske, annál nagyobb frekvenciájú forgás tartozik hozzá. Amikor az ősállapot kezdett lehűlni már elég volt az idő az ütközések között, hogy a legnehezebb részecskék kialakuljanak, majd később jöhetett létre a könnyebb elektron is. Az utána következő fázis már megfelelhet az ősrobbanás elméletének jelenleg elfogadott menetének. Van azonban az elméletnek egy gyenge pontja, mert nincs meggyőző magyarázat arra, hogyan vált uralkodóvá az anyag az antianyag felett. A nagy energiájú folyamatok a részecske fizika szerint egyszerre hoznak létre mindig egy részecskét és egy antirészecskét, ezért az annihilációs folyamatok nem tennék lehetővé az anyagban túlsúlyos univerzum kialakulását. Ez a dilemma feloldható kaotikus fénysebességű mozgások esetén, mert ekkor a véletlen szabályai uralnák, hogy a rendezetlen mozgásokból éppen milyen részecskék alakulhatnak ki, tehát ekkor nem kötelező, hogy egyidejűleg részecskepárok jöjjenek létre. A részecskék és antirészecskék száma a statisztika szabálya szerint eltérhetnek egymástól és így a rendezetlen ősállapotból a rendezett forgások világába átmehetett az univerzum a protonok és elektronok véletlen szülte többlete által.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

Színhely: Műcsarnok, 2015 december 5

Az emberi gondolkozás szintjei az ókori , mai, a fizikáé, enyém, hallgatóságé

Szemléltetés: az ősrobbanás és a teremtésmítoszok kapcsolata

Vita: rövid kérdések közben, a végén lehet hosszabb álláspontokat kifejteni.

Az ókor: teljesség,  modern kor fragmentált, leszűkített gondolkozására.

Módszer: Virtuális diák

Dia 1: A valóság, mint fizikai objektum, szétdarabolás, alak?

Dia 2. Puzzle: A részek ismerete nem tárja fel a motívumot

Dia 3. Bábel tornya és a tudomány szétaprózottsága. C.P. Snow: A két kultúra (humán és reál)

Cél: összeillesztés az egyes elemek ismeretében

Szakterület: elektronok mágneses tulajdonságai, aminek alapja a spin

Mi a spin? A Dirac egyenlet által bevezetett fizikai mennyiség.

Összhang keresés: Átfogó, ellentmondásmentes fizikai szemléletmód kialakítása a fizikában

Negatív fizikus vélemények.

Mi a modern fizika gondolkodásmódjának legfőbb hibája:

Belevész az egyenletekbe és eltolja magától a fizikai fogalmak értelmezését

Cél: Összességében látni a fizika világát, melynek alkotóeleme az ősrobbanás

Fizikai elvek kimondása matematikai egyenletek helyett!

Impulzus, erő és energia

Kulcs: az állandóság és a változás viszonya

Dia 4: piruett figura a jégtáncban

Dia 5: Kerekes kút

Impulzus-nyomaték, spin

Hogyan lehet egy pontszerű részecskének nyomatéka?

Az összeillesztés módja

Elem_1: speciális relativitáselmélet: Mi az alapelv? A kölcsönhatások véges sebessége. Ez egy még általánosabb törvényből adódik: egy VÉGES rendszerben minden tulajdonságnak végesnek kell lenni.

ÁLLANDÓ:  fénysebesség

VÁLTOZÓ (relatív) : tömeg, távolság

Elem_2: a foton fénysebességgel terjed: nulla nyugalmi tömeg, de E = m.c²!

Elem_3: X*1/X = 1  A nulla és végtelen szorzata lehet véges!

A fénysebesség tömeget (anyagot) hozhat létre!

Elem_4: részecskefizika

Minden tömeget a fénysebességű mozgás hoz létre! Nyugalmi tömeg: lokális mozgás, fénysebességű forgás, anyag és antianyag, elektron, pozitron, neutrínó, kvarkok

Elem_5: Általános relativitáselmélet: Elv: a tér torzulása a gravitációs erő forrása

Dia 6:  Gumimatrac

Elem_6: Kvantummechanika, kvantum: a fénysebességű forgás impulzusnyomatéka

Elem_7: Az ősrobbanás:  Georges Lemaître (ősatom), Fred Hoyle (steady-state univerzum),  Edwin Hubble (galaxisok vörös eltolódása: táguló univerzum). Mi vagyunk a világ közepe?

Dia_7: kocka alakú dobozok

Kínai eredetmítosz: „Az ég naponta három méterrel emelkedett magasabbra, a föld három méterrel vastagodott. Így folytatódott ez 18 ezer éven át, míg az ég elérte a legnagyobb magasságot, és a föld a legnagyobb mélységet”

Polinéz:  Az istenek seregéért van az éj,

Az emberekért van a napvilág.

Az éjben csak az istenek születnek kitágulása óta ennek a világnak…

Nagyobbodott Tumu-nui, nagyobbodott Papa’raharaha, nagyobbodott (az isteneknek és az embereknek) háza, nagyobbodott az égnek alja.

Nőttön-nőtt az ég, szélesbedett az ég, és vele Havai’i földjének cölöpei.

Mi az a hajtóerő, ami az univerzum tágulását előidézi?

Elem_8: Termodinamika. Elv: entrópia. Változás iránya: a valószínűbb (többféleképpen megvalósuló) állapot felé történik

Dia_8: szita és dobókockák

Dia_9: gyöngyök

Kezdeti forró átmenet szakasza: Az óriási hőmérsékleten az ütközések szétverik az atomokat , az atommagokat sőt azok alkatrészeit a nukleonokat is. Ez a kvarkok és gluonok kaotikus plazma állapota?

Dia_10: Piruett a zsúfolt jégen

Szerintem: kaotikus fénysebességű lüktetés. Nincs idő a forgások kialakulására a túl gyors lüktetés miatt. A forgási frekvenciának is van felső határa! Evolúció: a rendezetlen lüktetésből alakul ki a rendezett forgások, azaz a kvantumok világa. Nukleonok, atommagok, atomok, égitestek, galaktikák

Polinéz: Tane üdvözölte Ra’i-tupu’át és így szólott hozzá: „Kelj fel Ra’i-tupu’a és tedd, ami dolgod! Tétessen a helyére a kavargó ég, hogy rend legyen és gyönyörűség!”

Ra’i-tupu’a ekkor helyére tette a kavargó eget. Mint ahogyan a kézművesek rendezik a csónakok pallóit, úgy dolgozott Ra’i-tupu’a a kavargó égen.

Tane gondosan felmérte az egeknek űrét, egének palástját.  Ra’i-tupu’a azután helyére tette a Holdat és a Napot és a csillagokat a tengerkék égben alulról, miközben Ma-tohi rögzítette a helyükön a magasban.

A Nap járásának lassítása

Az anyag kialakulása plasztikusan jelenik meg az indiai mitológiában:

Indiai: „Az egyetemes anyag legfinomabb rezgéseiből létesült a felső kör; a középső kör átmenet volt a finom rezgésű anyag síkjai között; az alsó körben pedig az anyag legsűrűbb, ütköző, nehézkedő rezgései bontakoztak szét megszámolhatatlan alakzattá.”

Az őselem koncepciója is megjelenik az egyiptomi mitológiában:

Egyiptomi: „Kezdetben nem volt sem ég, sem föld, sem élők, sem holtak nem voltak, az alkotó és romboló elemek is dermedt tétlenségben nyugodtak Nun isten örvénylő mélyén. Nun volt az őselem, az ősvíz formájában létező istenlény. Az ő alkotórészeiből keletkezett a mindenség.”

A kínai mitológiában az ég és föld teljes egysége mutatkozik meg:

Kínai: „Kezdetben, amikor az ég és a föld még tojás alakú káosz volt, Pan Ku megszületett a tojásban, és itt élt tizennyolcezer esztendeig. És ekkor a Jang tiszta elemeiből megformálódott az ég, a Jin durvább elemeiből pedig a föld. Pan Ku a középpontban tartózkodott, és nap mint nap kilenc alkalommal alakult át: hol az ég, hol pedig a föld istene volt.”

Az egy-isten hit a kiindulópontja a teremtésnek (Visnu, Pan Ku, Nun, Apszi, Ta’aroa):

Ta’aroa benn nyugodott a burkában, az éjben, a legrégibb  időktől fogva.

Mint egy tojás olyan volt a burok, forgott az űrben, nem volt ég, sem föld, sem hold, sem csillagok. Az éj volt csak egyedül, a végtelen éj, az áthatolhatatlan sötétség…

Hogy alakul ki a föld, ami Japánban a szigeteket jelentette a káoszból:

Japán: „Izanagi és Izanami letekintettek a Menny Lebegő Hídjáról, és azt fürkészték, van-e föld valahol a híd alatt. Csillogó drágakőből hatalmas lándzsát készítettek, a fegyvert lehajították, és rábukkantak a tengerre. Ezután kiemelték a lándzsát a káoszból, a káosz cseppenként aláhullott, megszilárdult, és így keletkezett Onokoro-Jima, a Megdermedt Sziget.”

A tibeti mitológiát a filozófia megfogalmazás tökéletessége jellemzi:

Tibeti: „Kezdetben semmi sem létezett, sem tér, sem idő, sem valóság, sem jel, sem lét, sem nemlét. Ebből keletkezett minden, ami látható és tapintható.

Az első lény varázslatos átalakulási képességgel született. Megnevezte magát: "A Keletkező Világ Ura, Szent Győzedelmeskedő". És boldog volt, mert hatalma mindenre kiterjedt.”

Az ősrobbanás elmélet szerint az első másodpercben több minden történt, mint a rákövetkező 13,7 milliárd év alatt! Fokozatosan alakultak ki a nukleonok, majd az atommagok és jóval később az atomok.

Görög időfogalmak: kronosz és kairosz. Fizika: mérési utasítás. Hogyan mérjük az időt a „forró” univerzumban?  Eseménysűrűséggel. Ha az események exponenciális sebességgel változnak, akkor a logaritmikus idő adja a jó skálát! Ebben a Planck-idő 10^-43s -43 lesz, az egy másodperc  lesz a nulla, mai korunk 17,635. Az ősrobbanás logikai ellentmondás! Mi volt az ősrobbanás előtt? De az „előtt” idő fogalom, aminek nincs értelme, ha nincs univerzum. Ez a fizikai gondolkozás csapdája. Ha a világ keletkezését magyarázni akarjuk, akkor ki kell lépni a szűk fizikai gondolkozás kereteiből. Az anyagi valóságból nyert fogalmaink nem magyarázhatják az anyagi világ keletkezését, csupán az evolúcióját.

Az ókori gondolkozás titka: a világot – beleértve a szellemi és anyagi világot is – annak egységében látták. Az ég és a föld, az isten és az ember, az ideák és a dolgok világa egységében jelenik meg.

Az ideák létrejötte a tibeti mitológiában:

Tibeti: Ekkor a négy évszak még nem vált el egymástól, a nap, a hold, a bolygók és a csillagképek alig mozdultak, a mennydörgés, a villámlás, az eső, a jég, a fagy sem követték az évszakok változásait. A földnek nem volt ura, az erdők, a növények maguktól nőttek és szaporodtak. A kövek és a hegyek már létrejöttek, de még nem mozdultak, és a földrengés is ismeretlen volt. A föld aranyból volt. A folyók is megvoltak már, de még nem indultak el a tenger felé. Madarak és vadak is éltek az erdőkben, de még senki sem vadászott rájuk. Istenek is léteztek, de még nem hallgatták meg a könyörgéseket, és nem uralkodtak ég és föld felett. Létrejöttek a démonok is, de még nem kezdhették el romboló munkájukat. Voltak betegségek, de még nem okoztak kínt és fájdalmat. Volt már táplálék, de még senki nem fogyasztotta. A boldogság is létezett, de nem volt, aki felfogja. A nappal nem különbözött az éjszakától.

Hogyan alkot a szobrász? Az ideák teremtése megelőzi a dolgok teremtését. A platoni ideák évezredekkel Platon előtt léteztek, Platon csak összefoglalta az ókori bölcseletet. Arisztotelész a választó vonal, amikor megszűnik az egységben gondolkozás, szétválik az ideák és a dolgok világa, leválik az anyagi természetről való gondolkozás a szellemiről. Ez a fragmentált modern gondolkozás kezdete

Mi a teremtés:  nyugvó gondolat: ideák, megrezdült gondolat (megnevezés):  dolgok

Indiai : A Világéjszaka sötét, mindent elborító, mozdulatlan tengerének színén összecsavarodva nyugodott Ananta, a Végtelenség Kígyója, s rajta álomba merülve pihent Visnu, a mindenség létesítője és fenntartója, az egyetlen hatalom. Bensejében a világ egész tartalma mint nyugvó gondolat derengett, rajta kívül nem volt élet, nem mozdult semmi. Álmában egyszerre megrezdült benne a gondolat, és Visnu felébredt. Kinyitotta szemét, és látott. Abban a szempillantásban megindult a mozgás az odáig nyugvó ősanyagban. Visnu létesítő akarata kisarjadt, és köldökéből egy lótusz nőtt elő. A lótusz széttárta szirmait, és íme, a lótusz kelyhében ült Brahmá, az Egynek Teremtő Ereje.

Mezopotámiai:  Midőn fönn az ég nevetlen s alant a föld szintazonképp;

Apszu, az ős-kezdet, minden dolgok teremtője-atyja

s Mummu-Tiámat ősanyánk még vizeikkel egybemosódtak;

nem volt szárazföld se, láp se, s egyike sem az isteneknek;

név nélkül szunnyadott a sors is, betöltetlen várt a végzet

Maja: Elmélkedtek (az istenek), és íme, megvilágosodtak, megjelent az Ősfényhajnal, és terveikben megjelent az ember.

Ennek utána elgondolták a teremtést, elgondolták a fák és folyondárok növekedését, az élet születését és az ember alkotását és a sötétségben és fénytelen éjszakában ekképpen szerezte mindezt Égszíve, az, akit Hurakánnak mondanak...

Miképpen legyen élet, és miképpen jöjjön létre világosság? Kinek kell gondoskodnia táplálékról és betévő falatról?

- Jöjjön immár, és legyen! Népesüljön be az üresség!

Az ég teremtése megelőzi a földét, a világosság teremtése megelőzi a Napét:

Mózes: 1. Kezdetben teremté Isten az eget és a földet.

2. A föld pedig kietlen és puszta vala, és setétség vala a mélység színén, és az Isten Lelke lebeg vala a vizek felett.
3. És monda Isten: Legyen világosság: és lőn világosság.
4. És látá Isten, hogy jó a világosság; és elválasztá Isten a világosságot a setétségtől.
5. És nevezé Isten a világosságot nappalnak, és a setétséget nevezé éjszakának: és lőn este és lőn reggel, első nap.

Ősrobbanás elmélet: 380 ezer év után jöttek létre az atomok, ezáltal lett átlátható, azaz világos az univerzum. Ennek nyoma a mikrohullámú háttérsugárzás. A csillagok és galaxisok képződése csak jóval később jöttek létre.

Mózes: 14. És monda Isten: Legyenek világító testek az ég mennyezetén, hogy elválasszák a nappalt az éjszakától, és legyenek jelek, és meghatározói ünnepeknek, napoknak és esztendőknek.

15. És legyenek világítókul az ég mennyezetén hogy világítsanak a földre. És úgy lőn.
16. Teremté tehát Isten a két nagy világító testet, a nagyobbik világító testet, hogy uralkodjék nappal és a kisebbik világítótestet, hogy uralkodjék éjjel; és a csillagokat.
17. És helyezteté Isten azokat az ég mennyezetére, hogy világítsanak a földre;
18. És hogy uralkodjanak a nappalon és az éjszakán, és elválasszák a világosságot a setétségtől. És látá Isten, hogy jó.
19. És lőn este és lőn reggel, negyedik nap.

A blog további írásait összefoglaló bejegyzés: "Paradigmaváltás a fizikában." 

Miért relativisztikusak a fizikai törvények?

A modern fizika törvényeit azért nehéz befogadni, mert következtetései gyakran nem követik gondolkozásunk megszokott menetét.  Erre példa a relativitáselmélet és a kvantummechanika világa. Itt most bonyolult matematikai formulák felhasználása nélkül kívánom bemutatni, hogyan lehet köznapi logikánk segítségével érthetővé tenni, az egyébként a józanésszel ellentmondani látszó fizikai törvényeket is.

Mi következik az univerzum létezéséből?

Kiindulópontunk egy olyan állítás, amit aligha von kétségbe bárki is: az univerzum létezik! Ebből az egyszerű állításból szinte az egész relativitáselmélet levezethető! Az ősrobbanás elmélete szerint az univerzum már régóta, hozzávetőleg 13,7 milliárd éve létezik, és nem mutat semmi jel arra, hogy hirtelen fel akarna robbanni, vagy eltűnni. Univerzumunk tehát stabilis képződmény. De lehetséges lenne ez, ha nem lenne határa a kölcsönhatások sebességének, ha az univerzum bármely pontja késleltetés nélkül megváltoztathatna valamit az univerzum egy másik pontján?  Gondoljuk végig, hogy mi is történne ilyenkor? Természetesen ekkor minden hatásra késleltetés nélkül jönne a válasz. A válaszra pedig azonnal viszontválasz születne. Az egyidejűleg jelentkező végtelen sok hatás és viszonthatás összegeződne, aminek eredménye vagy robbanás, vagy egymás kölcsönös megsemmisítése lenne. Az univerzum tehát nem lehetne olyan stabilis, ami jellemzi az elmúlt néhány milliárd évet. Az univerzum létezése ezért megköveteli, hogy a hatást késleltetve kövesse a válasz, azaz a kölcsönhatások sebessége véges legyen.

A kölcsönhatások határsebessége

Két olyan távolba ható kölcsönhatás van, ahol gyakorlati jelentősége van a kölcsönhatások véges sebességének, az egyik a gravitáció, a másik az elektromágneses kölcsönhatás. Elképzelhető, hogy eltérő a sebessége a két kölcsönhatásnak?  A töltéssel rendelkező fizikai objektumok, például az elemi részecskék tömeggel is rendelkeznek. Ha eltérne egymástól a két kölcsönhatás sebessége, akkor szétválna egymástól a két hatás. Például már éreznénk egy objektum gravitációs vonzását, de elektromos hatása még nem érkezne meg. Ez a megfigyelő számára kettéválasztaná a fizikai objektumot: az egyik már létezne a számára, a másik még nem. Ez szétszakítaná fizikai világunkat, ezért csak olyan lehet a világunk, amelyben a két nevezett kölcsönhatás sebessége azonos. Ezt szemléltetendő képzeljük el, hogy egy a Napnál sokmilliószor nagyobb és fényesebb csillag száguldana el naprendszerünk külső határán, úgy egyfényévnyi távolságban. Ennek hatására áradás indulna meg a tengerekben és az éjszaka is olyan világos lenne, mint a nappal. De mikor vennénk ezt észre? Nem akkor, amikor a legközelebb lenne ez a csillag, hanem csak egy évvel később. A gravitációs és a fényhatás viszont egyszerre érkezne el hozzánk. Evvel logikai úton eljutottunk a relativitáselmélet fontos törvényéhez, mely szerint minden kölcsönhatás a fény c sebességével terjed.

Mi az inercia rendszer?

A relativitáselmélet törvényei azért vannak távol mindennapjainktól, mert csak olyan sebességi tartományban van jelentős hatásuk, amikor már a fény irdatlan sebességéhez közel járunk. Ismert hasonlat, hogy a fény egyetlen másodperc alatt hét és félszer lenne képes körüljárni a Földet. Képzeljünk most magunk elé egy másik világot, ahol sokkal alacsonyabb a határsebesség, legyen mondjuk 100 km/óra. Szálljunk fel egy vonatra, amelyik éppen 99 km/óra sebességgel száguld. Ha a vonat sebessége állandó és nem láthatjuk a külvilágot és nem halljuk a kerekek zakatolását sem, akkor nem is tudjuk, hogy állunk-e vagy nagy sebességgel haladunk. Ekkor semmi nem változik a vonaton, nem fog más ütemben mozogni óránk mutatója sem. Az ilyen rendszert nevezi a mechanika inercia rendszernek. Észrevesszük azonban, ha a vonat gyorsul, vagy lassul, mert akkor a tehetetlenség miatt hátra eshetünk, vagy előre, ha nem kapaszkodunk.

A sebességek relativisztikus összegzési szabálya

Ezen az állandó sebességű vonaton tegyünk néhány lépést a vonat haladási irányában 5 km/óra sebességgel és menjünk át a 10 m hosszú szerelvény másik végébe. A vonaton kívüli pontokhoz képest mekkora sebességgel fogok mozogni? Ez nem lehet 99+5 = 104 km/óra, mert ez már meghaladná a határsebességet, a tényleges sebesség ezért még 100 km/óra alatt fog maradni. Evvel eljutottunk a relativitáselmélet egy meglepő törvényéhez: a sebességek nem adódnak össze a szokott módon. Szemléltessük ezt egy gondolatkísérlettel.  Legyen valaki a sínek mellett, aki egészen közelről egy fényjelet ad le, amikor a szerelvény egyik végében vagyok. A jel olyan közelről érkezzen, hogy ne kelljen számításba venni, hogy mennyi idő alatt jut el hozzám. Abban a pillanatban, amikor a szerelvény másik végébe értem én adok le egy fényjelet valakinek, aki szintén a sín mellett áll. A két ember órája alapján meghatározzák az időt, majd evvel osztva a távolságukat megkapják, hogy mekkora volt hozzájuk képest az én sebességem. Ez nem lehet 100 km/óránál több, mert ha így lenne, akkor sikerülne a két ember között az információt a határsebességnél gyorsabban továbbítani.

A távolság relativisztikus csökkenése: Lorentz kontrakció

Hogyan lehet, hogy hiába tettem meg 10 métert 5 km/óra sebességgel a vonathoz képest mégsem léphettem át a sebességhatárt? Ennek oka, hogy a vonatot kívülről nézve a szerelvény hossza összezsugorodik, tehát kívülről nézve én nem 10 métert tettem meg, hanem rövidebbet. Itt hangsúlyozni kell, hogy ez a rövidülés, amit Lorentz kontrakciónak hívnak a külső és a vonathoz képest 99 km/óra sebességgel elmaradó megfigyelő rendszerére vonatkozik. Hasonlóan, ha a sínek mellett 10 méterenként oszlopok vannak, akkor a vonatból megfigyelve ezek távolsága kisebb lesz. Tehát a zsugorodás relatív, attól függ, hogy melyik inercia rendszerből határozzuk meg egy másik inercia rendszerben lévő távolságot.

Relativisztikus tömegnövekedés

De nem csak a távolság és a sebesség függ az inercia rendszer relatív sebességétől, hanem a tömeg is. Ha valaki 10 méterre képes eldobni egy súlygolyót, de mi a dobást a vonat ablakából figyeljük meg, akkor úgy látjuk, hogy a dobás hossza rövidebb. Ezt a Newton törvény alapján úgy értelmezzük, hogy a dobó csak kisebb gyorsulást adott a golyónak, mert a ténylegesnél nagyobb a tömege. Így jutunk el a tömegnövekedés törvényéhez. Tehát minden relatív, a távolság, a sebesség és a tömeg is, csak egy dolog van, ami minden inercia rendszerben azonos, ez pedig a határsebesség!

A fénysebességű mozgás hatása

De mi történne a 100 km/óra sebességű vonaton? Itt bármekkora sebességgel mozognék a vonaton kívülről nézve az én sebességem mindig 100 km/óra maradna, ami azt jelentené, hogy ekkor a szerelvény hossza nulla lenne, és így hiába mennék át a szerelvény másik végébe nem növekedne tovább a teljes sebesség. A nulla hossz pedig azt jelentené, hogy az eldobott súlygolyó nem repülne el egy parányit sem, mert a tömege végtelenül nagyra növekedne. A tömegnövekedési szabály persze a vonatra is vonatkozik, ezért a vonat sem érhetné el a határsebességet. Mégis van valami, ami képes határsebességgel mozogni, ez pedig maga a fény, illetve annak kvantuma a foton. Ez viszont megköveteli, hogy a foton tömege nulla legyen. Úgy mondhatjuk, hogy a nullatömegű objektumok privilégiuma, hogy fénysebességgel terjedjenek. De nem csak privilégiumuk, hanem „kötelezettségük” is, nullatömegű objektumokról csak akkor van értelme beszélni, ha fénysebességgel haladnak, ettől válnak "anyaggá" és ez megfigyelhetőségük kritériuma. A tömeg és energia ekvivalenciája E = m.c² a modern fizika egyik legfontosabb törvénye, ez minden fizikai objektumra, így a fotonokra is érvényes. Tehát a fotonoknak is van tömegük, de ez nem „nyugalmi” tömeg, ez a fénysebességű mozgásukból fakad. A fénysebességű mozgás azáltal, hogy végtelenszer megnöveli a nulla nyugalmi tömeget, létrehozhat valami végeset, amit mozgási tömegnek nevezhetünk. A matematika ezt úgy írja le, hogy a határértékben végtelenül kis mennyiséget végtelenhez tartó számmal szorozva véges mennyiséghez jutunk:

akkor is, ha X végtelenhez tartó mennyiség.

Az idő dilatáció és az ikerparadoxon

De nem beszéltünk még a relativitáselmélet legnehezebben megérthető jelenségéről, az idő dilatációról. Ha a vonatunk 99 kilométert tesz meg egy óra alatt, akkor a sebessége 99 km/óra. De hogyan ítéli ezt meg a vonaton utazó? Számára a távolság kontrakciója miatt úgy tűnik, hogy csak rövidebb utat tett meg, ezért ha ezt a rövidebb távolságot osztja el a sebességgel, akkor rövidebb menetidőt állapít meg, azaz számára az idő lassabban telik. Ez az idő dilatáció. A jelenség sajátos következménye az ikerparadoxon. Az ikrek egyike világkörüli útra indul, és nagy utakat tesz meg a fényét megközelítő sebességgel, majd évek múltán visszatér. Ez alatt ikertestvére megöregszik, míg ő fiatal marad. Ismételjük meg ezt a 100 km/óra határsebességű világban. Induláskor hasonlítsuk össze óránkat valakivel, majd utazzunk el a 99 km/óra sebességű vonattal, majd utazásunk végeztével térjünk vissza a kiindulópontra. A mi óránk ekkor kevesebbet fog mutatni. Ez látszólag ellentétes avval a megállapítással, hogy az állandó sebességű vonaton semmi nem változik meg az állóhoz képest, így az óra is ugyanolyan ütemben jár. De ebből a gondolatmenetből épp a lényeg hiányzik: csak úgy tudunk nagy sebességgel utazni, ha előzőleg felgyorsult a vonat, majd visszafele lelassult. Amikor nem vagyunk inercia rendszerben már más szabályok érvényesek a tehetetlenségi erő megjelenése miatt. Ez pedig már az általános relativitáselmélet területe, ahol a gravitáció forrása a tehetetlenségi erő.  A valódi világban, ahol a fénysebességet kell megközelíteni, igen intenzív gyorsulásra illetve lassulásra van szükség, amelyik az óriási tehetetlenségi erő miatt lassítani fogja óránk járását, más szóval az eltelt időt. Megtudjuk ebből, hogy hol kell keresni az örökfiatalság titkát: az állandó gyorsulásban.

Hogyan jön létre a tömeg?

A fény kvantumáról, a fotonról megállapítottuk, hogy a fénysebességű mozgás révén energiára, azaz mozgási tömegre tesz szert. Vajon nem lehet, hogy minden fizikai objektum, az összes elemi részecske is, valamilyen fénysebességű mozgásnak köszönheti tömegét?  Induljunk ki a foton tulajdonságaiból és nézzük meg, hogyan vihetjük át annak fizikai jellemzőit az elemi részecskére. A foton energiája frekvenciájától függ, viszont bármekkora is a frekvencia az impulzusnyomaték mindíg hajszálra azonos, amit a ℏ Planck állandó ad meg. Ugyanez a Planck állandó köti össze a frekvenciát az energiával az E = h.ν = ℏ.ω szabályon keresztül. A fotonnak impulzusa is van p = h.ν/c értékben. Ez viszont közvetlen kapcsolatot jelent az energia és az impulzus között: E = p.c. Tehát a fénysebességet úgy is értelmezhetjük, hogy ez az energiát és impulzust összekötő arányossági tényező.

Honnan származik a foton impulzusnyomatéka?

Impulzusnyomaték létezése két dolgot kíván meg: forgást és forgási sugarat. Az ω frekvenciát értelmezhetjük a forgás szögsebességének, és ha a forgás kerületi sebessége c, akkor a sugár is értelmet nyer r = c/ω. Mivel az impulzusnyomaték a szögsebességgel és az objektum sugarával arányos, így már arra a kérdésre is választ kapunk, hogy miért azonos ez a nyomaték bármekkora is legyen az ω szögsebesség. A foton forgása mellett fénysebességgel terjed is, azaz mozgását mint egy  fénysebességű forgás és haladás kombinációját adhatjuk meg.

Az elemi részecskék impulzusnyomatéka

Az elemi részecskék, mint például az elektron és a proton (tehát a fermionok) szintén rendelkeznek impulzusnyomatékkal, aminek értéke ℏ/2, azaz fele akkora, mint a fotoné. A fotonnal szemben viszont rendelkeznek nyugalmi tömeggel és nem mozoghatnak fénysebességgel. Ahogy a fotonnál kétféle fénysebességű mozgás (forgás plusz haladás) hozza létre a mozgási tömeget, így az elemi részecskéknél is lehet kétféle mozgás, ami végül létrehozza a nyugalmi tömeget, de mivel itt a haladás sebessége nem lehet c, így kézenfekvő a feltételezés, hogy mindkét mozgás forgásként valósul meg. Az elemi részecskék nem rendelkeznek kitüntetett iránnyal, azaz forgásuk csak gömbszimmetrikus lehet. A kétféle forgás együttese ezt a kritériumot is teljesíti. Minden forgás centrifugális erőt kelt, a forgást ezért valamilyen centripetális erőnek ellensúlyozni kell. Ezt biztosítja a korábbi bejegyzésekben már tárgyalt erős gravitáció, ami a fénysebességű forgások által létrehozott extrém mértékű tértorzulás által jön létre (lásd az általános relativitáselmélet alapelvét). Fermionok esetén az erős gravitációnak két különböző forgással kell egyensúlyt tartani, ezért lesz az elemi részecskék impulzusnyomatéka fele akkora, mint amekkorával a foton rendelkezik.

A speciális relativitáselmélet energiaegyenlete

Értelmezzük úgy a speciális relativitás alapelvét, hogy az valamennyi részecske esetén az energia és az impulzus arányosságát fejezi ki, ahol az arányossági tényező a c fénysebesség: E = p.c.

A részecske impulzusának két összetevője van: p₀ fejezi ki a sajátmozgást, p₁ a tömeggel rendelkező objektum mozgását a külső térben, azaz

p = p₁ + p₀

Itt a félkövér betű fejezi ki, hogy az impulzus vektoriális mennyiség szemben az impulzus nagyságát megadó skaláris kifejezéssel.  Képezzük az energia és impulzus kapcsolatának négyzetét:

A gyors sajátforgások hatásának csak a várható értékét figyelhetjük meg. A gömbszimmetrikus mozgások miatt <p₀> = 0, így a négyzetre emeléskor a kereszttag eltűnik:

Ez pontosan megfelel a relativisztikus energiaegyenletnek, mely szerint

A két egyenlet azonossága miatt p₀ = m₀.c, ami annak felel meg, hogy az m₀ nyugalmi tömeg valójában a fénysebességű mozgás által tesz szert impulzusra. Evvel kimutattuk, hogy a speciális relativitáselmélet energiaegyenlete az energia és az impulzus arányosságára vezethető vissza. A törvényt eredetileg makroszkopikus testekre állapították meg, de ennek azaz alapja, hogy valamennyi elemi részecske energiája ugyanúgy épül fel a kinetikus és a nyugalmi energiát leíró tagokból.

Összefoglalás

A stabilis univerzum létezése megköveteli, hogy minden kölcsönhatásnak véges legyen a határsebessége, ami a fénysebesség, és ebből következnek a relativitáselmélet törvényei is. A fénysebességű mozgás hozza létre a tömeggel rendelkező anyagot. A határsebesség köti össze az energiát az impulzussal, és ez az összefüggés az alapja a relativisztikus energiaegyenletnek.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.

Az írás második részében ismertetem a ma széles körben elfogadott ősrobbanás elmélet alapjait és kiegészítem a részecskék fénysebességű mozgásából fakadó következményekkel. Az ősrobbanás tükrözi a modern ember gondolkodásmódját, amely a tudományokra alapozott hitre épül. Az ókori kozmológiát a fantázia szabad szárnyalása jellemzi, míg napjainkét a különböző tudományok eredményeinek összevetése. Megjelenik benne az általános relativitáselmélet koncepciója a gravitációról, a részecske fizika törvényei, a kvantumelméletek összefonódása és a termodinamika is. Az elméleti megfontolásokat pedig a csillagászati megfigyelések támasztják alá. Jelentős sikereket mutathat fel az ősrobbanás elmélete, de legalább ennyi kérdésre nem tud válaszolni. Ez utóbbira néhány esetben a fénysebességű forgások koncepciója adhat útmutatást. A legfőbb megválaszolatlan kérdés azonban fennmarad: hogyan lehet átlépni a lét és a nem-lét határát, vagy más fogalmazásban miért következett be egyáltalán az ősrobbanás? Erre a kérdésre a tudomány nem is adhat igazi választ! Az ősrobbanás elméletére ezért úgy tekinthetünk mint napjaink mitológiájára.

Az elmélet születése

Talán nem is véletlen, hogy az elmélet alapjait egy katolikus pap, Georges Lemaître dolgozta ki. Kiinduláspontja Einstein általános relativitáselmélete volt, amivel a spirális galaxisok távolodását kísérelte meg leírni. Már 1927-ben felvetette az „ősatom” koncepcióját feltételezve, hogy a galaxisok távolodása az univerzum alapjelensége, amit visszavetítve a messze múltba, kellett lenni egy olyan kezdő pillanatnak, amikor az összes galaxis egyetlen matematikai pont volt, amelyben az egész univerzum összes energiája benne foglaltatott. Meghökkentő állítás, ha arra gondolunk, hogy milyen óriási energia van a Napban és a Nap csak egy szerény csillag a Tejútrendszer milliárd csillagja közül, és a galaxisok száma is eléri a milliárdot! Szabad-e ilyen messzire extrapolálni, mi a garancia arra, hogy a fizika törvényei változatlanok ilyen extrém körülmények között, amikor a nyomás, az anyagsűrűség és a hőmérséklet elképesztő mértékben megemelkedik? A fizikusok többsége ezért sokáig inkább Fred Hoyle hipotézisét fogadta el, amelyben állandó állapotú (steady state) univerzumot tételezett fel, szerinte a tágulás tömeget hoz létre és így az univerzum tömegsűrűsége és hőmérséklete mindig állandó marad. 

Hubble tágulási törvénye

A tágulási törvényre Edwin Hubble talált bizonyítékot, amikor 1929-ben a galaxisok vöröseltolódása alapján kimutatta, hogy a távolodás sebessége arányosan növekszik a távolsággal, tehát a közeli galaxisok lassan, a távolaik gyorsan távolodnak. (A vöröseltolódás Doppler-jelenség: ahogy a távolodó vonat hangja mélyül, úgy csökken az atomok által kibocsátott fény hullámhossza is, azaz a látható tartományban a kék szín a vörös felé tolódik el).

Itt álljunk meg egy pillanatra, hogy értelmezzük az univerzum tágulását. A térnek csak ott van értelme ahol anyag is van (az anyag fogalmába értsük bele a fényt is!). Tehát az univerzum nem a tőle függetlenül létező térben tágul, hanem magának a térnek tágulásáról kell beszélni. Képzeljünk magunk elé egy háromdimenziós rácsot, amelyet egyforma kockák alkotnak. Ez reprezentálja a teret, amelyben a galaxisok elhelyezkednek. Minden egyes kocka azonos sebességgel tágul, emiatt minél távolabb van két kocka, amely magában foglal egy-egy galaxist, annál gyorsabban fog a közöttük lévő távolság növekedni. A tágulásnak nem kell ezért, hogy legyen valamilyen centruma (bár lehet), az univerzum bármely pontjában ugyanaz a tágulási szabály érvényesül. Az egyes kockákban a galaxisok mozoghatnak, ahogy a bolygók is keringenek a napjuk körül, vagy a csillagok mozognak a galaxisban, vagy a galaxisok is vándorolnak egymáshoz képest. Ha közel van a galaxis, akkor a saját mozgás lehet gyorsabb is, mint a „kockák” tágulása. Példa rá a közeli Androméda köd, amelyik közeledik a Tejútrendszer felé. Viszont a távoli nagysebességű galaxisoknál a saját mozgás sebessége kicsi a táguláshoz képest, ezért ezekre a Hubble-törvény már pontosan érvényesül. A kockák alakja azonban nem tökéletes, eltérhetnek egymástól az egyes oldalak. Ez a makro torzulás hozza létre a gravitációt az általános relativitáselmélet szerint. De van számtalan apró torzulás is a kockákon belül, amit a részecskék fénysebességű forgása hoz létre, ez a részecske sajátforgását stabilizáló erős gravitáció. A sok-sok apró mikro torzulás – azaz részecske – száma határozza meg, hogy mekkora az egyes kockák makro torzulása, azaz a szokásos gravitáció.

Az ősi forró univerzum

Az ősrobbanás elméletével lépésről-lépésre ismerkedjünk meg. A kezdeti rendkívül forró és sűrű állapot a tágulás miatt hűlni kezd. Ez a termodinamikából következik. Hozzá rendelhetünk az univerzumhoz entrópiát is, amelyik növekedni fog a hőmérséklet csökkenése miatt (lásd még az „Energia, entrópia és evolúció” című bejegyzést). A rendkívül intenzív hőmozgás szétveri az általunk ismert elemi objektumokat is, nincs ezért sem molekula, sem atom, sőt atommagok és az összetevő nukleonok (proton és neutron) sem létezhetnek. Ezt az állapotot úgy szokás leírni mint a kvarkok és gluonok rendezetlen plazmáját. (Evvel a felfogással viszont már vitatkoznék, mert minden eddigi kísérleti adat arra mutat, hogy a kvarkok csak a hadronokban (mezon és barion típusú elemi részecskék) létezhetnek, de önállóan nem figyelhetők meg. Mi a garancia arra, hogy éppen a rendkívül nagy termikus mozgások birodalma teszi lehetővé önálló megjelenésüket? Erre a kérdésre később még visszatérek.) A lehűlés tehát megnöveli az univerzum teljes entrópiáját, de ugyanakkor létrejönnek azok a lokális „szigetek”, ahol már életképesek maradnak az összetett objektumok, mint az atommagok, majd az atomok és a molekulák. Az entrópiát mint a rendezettség mértékét lehet definiálni, ebben az értelemben az összetett objektumok létezése éppen hogy csökkenti az entrópiát, mert az alkotóelemek többé nem mozoghatnak szabadon, egymástól függetlenül. Ezt úgy foghatjuk fel, hogy a tágulás, amelyik egyrészt az univerzum teljes entrópiáját növeli, másrészt megteremti annak feltételét, hogy lokális centrumokban csökkenjen az entrópia.  Tehát az univerzum evolúciójának motorja az univerzum tágulása!

A világosság elválik a sötétségtől

Koncentráljunk most az univerzum fejlődésének egy fontos mérföldkövére, amikor annyira lecsökkent a hőmozgás intenzitása, hogy létrejöhettek az atomok. Ez azt jelenti, hogy a negatív töltésű elektronokat már elegendő erő kötötte hozzá a pozitív töltésű atommaghoz, elsősorban a protonokhoz, hogy kialakuljon a stabilis hidrogén atom. Evvel létrejött a semleges töltésű atomok világa. Ennek két szempontból is óriási jelentősége van.  Amíg csak szabad protonokról beszélhetünk a közöttük lévő erős elektromos taszítás nem tette lehetővé, hogy a gravitáció csillaggá forrassza egybe a protonok tömegét. Az elektronok és protonok egymásra találása viszont kiiktatta az erős taszítást és megalakulhattak a csillagok és a galaxisok a gravitáció mindent átható vonzásán keresztül.  A csillagok nagy energia- és anyagsűrűsége ugyanakkor begyújtotta a nukleáris folyamatokat és ennek révén a csillagok fénye bevilágította a sötét univerzumot. Ugyanakkor a szabad töltések eltűnése elvette a szabadon mozgó töltések fényabszorbeáló hatását, más szóval kitisztult az univerzum, átláthatóvá vált. Tehát a sötétség és a világosság szétvált egymástól! Gondoljunk most az ókori mitológiákra, például Mózes teremtés könyvére: a világ teremtésének kezdetén szétválik a világosság és a sötétség!

A kozmikus mikrohullámú háttérsugárzás

Az ősrobbanás elmélete szerint ez a pillanat a kezdetektől számítva 380 ezer évvel később következett be; és az akkor kiszabadult sugárzás azóta is áthatja az egész univerzumot, ez a nevezetes kozmikus mikrohullámú háttérsugárzás (CMBR , azaz Cosmic Microwave Background Radiation). Ennek megértéséhez tegyünk egy kitérőt a fizika fekete test sugárzásának törvényéhez.  Amikor az acélt felizzítjuk, kezdetben a vörös szín jelenik meg, majd tovább hevítve világosodik ki a színe a kék és a fehér felé. Ugyanezt figyelhetjük meg, ha a kályhánkban a tűz kialszik és a hőmérséklet csökkenésével a parázs vörös fénye szökik szemünkbe. A termodinamika szerint minden test sugárzik melynek színét (frekvenciáját) a hőmérséklet szabja meg. Ha alacsony a hőmérséklet, ez akkor is igaz, de ekkor a kibocsátott sugárzás már a szemünk által nem látható, de kellemesen melegítő, infravörös tartományba esik. Minél alacsonyabb a hőmérséklet annál kisebb lesz a sugárzás frekvenciája, lemehet egészen a mikrohullámú tartományba, sőt az alá is. Ezt a jelenséget nevezi a fizika a fekete test sugárzási törvényének. A sugárzás frekvenciájának értékéből ezért meghatározhatjuk, hogy mekkora a hőmérséklete a kibocsátó testnek. Az univerzum egésze is pontosan követi ezt a szabályt, amiből meghatározták a hőmérsékletet, amit 2,73 K-nak találtak. A háttérsugárzás jelenségét George Gamow 1948-ban jósolta meg az ősrobbanás koncepciójából kiindulva, majd később, már 1965-ben, ezt a sugárzást Arno Penzias és Robert Woodrow Wilson fel is fedezte (1978-ban Nobel Díjban részesültek). Ez a felfedezés fordulópontot jelentett az ősrobbanás elméletében, amit azóta fogad el a fizikus társadalom többsége.

Az univerzum korának logaritmikus időskálája

Különböző, itt nem ismertetett csillagászati megfigyelések arra az eredményre vezettek, hogy az univerzum kora 13,7 milliárd év. De hogyan is mérjük az időt a fizikában? Mindig valamilyen periodikus jelenségből indulunk ki, mint a Föld forgása, vagy egy kristály rezgése, az inga lengése, vagy a sugárzás frekvenciája.  Az univerzum kezdetén azonban nem voltak csillagok és bolygók, nem voltak atomok és molekulák sem, tehát nem léteztek azok a fizikai folyamatok sem, ami alapján elvben az időt mérni lehetne. Az ősrobbanás elmélete a kezdetekben az univerzum rendkívül gyors változását tételezi fel, eszerint az első másodperc alatt nagyobb változás következett be, mint az utána következő 13,7 milliárd évben. Az ősrobbanás előtti időről pedig nem lehet beszélni, mert a fizikai átalakulásokat, eseményeket jellemző időnek csak akkor van értelme, ha a fizikai világ egyáltalán létezik. Szükség van ezért a maitól eltérő időfogalomra, ha jellemezni akarjuk az univerzum evolúcióját. Mivel a kezdetekben exponenciális sebességgel zajlottak le az átalakulási folyamatok, ezért logikusnak tűnik, ha a mostani idő logaritmusával jellemezzük az univerzum korát. Számoljuk ki tehát a 13,7 milliárd évet másodpercekbe és adjuk meg ennek logaritmusát: 17,635. Az egy másodperchez tartozó logaritmus a nulla. Az ősrobbanás elméletek a 10^-43s Planck időig tekintenek vissza, mint a kvantummechanikai bizonytalanság miatt értelmezhető időhöz, tehát -43 LI-hez (LI = logaritmikus idő). Ez a skála már szemléletesen mutatja, hogy a -43 és a mai kor 17,635 LI logaritmikus ideje között jóval több minden történt az első másodpercben (tehát a nulla pontig), mint utána összesen! Az univerzumot logaritmikus idővel jellemezve elkerüljük a logikai csapdát is, amikor megkérdezzük, hogy mi volt az ősrobbanás előtt? Nem volt „előtt”, mert nem volt idő sem: a logaritmikus skálán tovább léphetünk -43 LI-it megelőző tetszőlegesen nagy negatív számig anélkül, hogy annak hatványa elérné a nullát. A logaritmikus időskálán tehát nincs kezdete az univerzumnak csak egyre régebbi és régebbi korszakai. Nem kell tehát feltételezni, hogy egykoron a nem-létből megszületett a lét. Az ősrobbanás csupán egy gondolati absztrakció, amikor végtelenül messze nyúlunk vissza az idő folyamatában.

A logaritmikus idő előképének tekinthető a görög kairosz, amit megkülönböztetnek az események kronológiáját leíró kronosztól. A kairosz megszentelt idő, a nagy pillanatok hírnöke. Ennek megfelelően a logaritmikus idő az univerzum nagy fordulatait, átalakulását jellemzi.

A Planck idő

„A véges és végtelen az Univerzumban” című írásban már foglalkoztunk a Planck idő szemléltetésével, amit itt egy kissé eltérő gondolatmenet alapján vezetünk be. A korábbi írásban felvetettük a kérdést, hogy van-e elvi határa az elektromágneses sugárzás frekvenciájának, azaz energiájának és a hozzá tartozó mozgási tömegnek. Induljunk ki a részecskék, így a fotonok, saját energiájának számításából. Ehhez azt a munkát kell alapul venni, ami ahhoz szükséges, hogy a részecskét felépítsük, ha végtelenül távolról rakjuk össze. A fénysebességű forgás modellje alapján az extrém mértékben torzuló tér ℏ.c/r potenciális energiája (erős gravitáció) ellensúlyozza az m.c² = ℏ.ω kinetikus energiát fotonok esetén. Az m mozgási tömegnek azonban van gravitációs hatása is, ami ha az r sugarú hengerpaláston található, akkor a gravitációs sajátenergia G.m²/r lesz (G a gravitációs állandó). Bármely részecskénél és a földi körülmények között megfigyelhető gammasugárzásnál ez a tag 30-40 nagyságrenddel elmarad az erős gravitációtól, ezért mérhetetlenül kicsi a járuléka. Más a helyzet, ha azt a határt keressük, ami a lehető legnagyobb energiájú sugárzáshoz tartozik. Ekkor az m.c² energiában már együtt kell figyelembe venni az erős és a szokásos gravitáció hatását:

Rendezzük át az egyenletet:

Ennek megoldása:

A foton mozgási tömege, azaz energiája csak valós értékű lehet, ami megköveteli, hogy a négyzetgyök alatti kifejezés pozitív legyen, vagy nulla. Ez meghatározza a sugár legkisebb értékét, amely a Planck hossz legalább kétszerese:

Ez behatárolja a foton ω = c/r frekvenciáját, ami maximálisan a Planck idő reciprokának fele lehet:

A gammasugár frekvenciájának felső határa ezért 10⁴³ Hz körül lehet, ami 17 nagyságrenddel haladja meg a földi körülmények között észlelt, illetve gyorsítókban a proton ütközések által létrehozható sugárzás energiáját. Ez azt jelenti, hogy az univerzum Planck korszakának földi laboratóriumban való tanulmányozására nincs esély.

A fénysebességű forgások kialakulása az ősi univerzumban

A fénysebességű forgások modelljében a fotont mint egytengelyű, a fermionokat (elektron, proton stb) mint kéttengelyű forgást értelmeztük. Forgásról azonban csak úgy beszélhetünk, ha legalább egy fordulatra sor kerül, aminek tartama a periódus idő. Ez azt jelenti, hogy a -43 LI-vel jellemzett korszak előtt még a legnagyobb energiájú foton sem jöhetett létre, ennél is jóval később alakulhatott ki a proton, amihez legalább -25, vagy az elektron amihez -22 logaritmikus időegység szükséges.  Ebben az időtartományban azonban még nem maradhattak meg a részecskék, mert a rendkívül magas hőmérséklet rendkívül gyors ütemű ütközéseket hoz létre, a stabilitáshoz az szükséges, hogy az átlagos ütközési idő hosszabb legyen, mint az egyes részecskék sajátforgásának periódus ideje.

Ez fejeződik ki az ősrobbanás elmélete által meghatározott időkben, amit protonok és a hasonló tömegű barionok esetén 10^-4 másodpercnek, azaz -4 LI-nek becsülnek. Még jóval később kerülhet az elektron stabil pályára a proton körül, aminek kötési energiája kilenc nagyságrenddel kisebb a proton nyugalmi energiájánál. Ennek ideje az a bizonyos 380 ezer év, ami a logaritmikus egységben 13,079 LI-nek felel meg.

Az ősrobbanás elméletét úgy szokás ismertetni, hogy a korai korszakban (-4 LI előtt) az univerzumot a kvarkok és gluonok plazmája alkotta. Evvel nem értek egyet, mert a kvarkok kisebb tömege miatt eleve nem jöhettek hamarabb létre, mint a nehezebb barionok és mezonok, másrészt semmi bizonyíték nincs arra, hogy a kvarkok létezhetnének szabadon is. A fénysebességű forgásmodellnek az felel meg, hogy a részecskéket alkotó forgások kialakulása előtt rendezetlen, kaotikus lüktetés jellemezte az univerzumot. Ebben a rendezetlen mozgásban fokozatosan alakultak ki a rendezett forgások, először a legkeményebb gammasugarak, majd később a gyenge kölcsönhatás W és Z bozonjai, majd a hadronok (barionok és mezonok) családja és még később az elektron és a pozitron. Az elemi részecskék három generációja közül mindig a nagyobb tömegű objektumok képződtek először.  Ennek az elképzelésnek mitológiai előképe, ahogy a káosz óceánjából előbukkan földi világunk.

A fizikai erők elkülönülése

A részecskék Standard Modellje négy erőt ismer: az elemi részecskék erős és gyenge kölcsönhatását, az elektromágneses és a gravitációs kölcsönhatást. Az ősrobbanás kozmológiájában úgy képzelik el, hogy kezdetben nem váltak még szét az erőhatások, csak az univerzum lehűlése sorén kezdtek önálló életet. Ismét egy mitológiai előkép, melyben a négy erőt a négy szél képviseli. Leválik tehát az erős kölcsönhatásról az elektrogyenge, majd később ezen belül is szétválik az elektromágneses és a gyenge kölcsönhatás. Az erőhatások szétválását a különböző kvantum mező elméletek alapján értelmezik, melyben minden egyes kölcsönhatásnak megvan a maga közvetítő bozonja: az elektromágneses kölcsönhatást a foton, a gyengét a W és Z bozon, míg az erős kölcsönhatást a gluonok hozzák létre. Az egész elmélet gyenge pontja, hogy a gravitáció mezőelméletét nem sikerült megalkotni.

Az általam képviselt felfogás szerint van egy ötödik erő, az erős gravitáció, amely biztosítja a részecskék sajátforgását. Az univerzum evolúciójának első fázisátmenete ezért az erős és a szokásos gravitáció szétválása, amikor kiválnak a kezdeti rendezetlen mozgásokból a rendezett forgások. A forgások hozzák létre a részecskék saját impulzusmomentumát, a spint. Ennek nagysága egytengelyű forgásoknál a ℏ (bozonok), a kéttengelyű forgásoknál ℏ/2 (fermionok). Amikor ezek a forgások kialakulnak, akkor jelenik meg a forgások alapegysége a kvantum is. A kvantumosság tehát nem egy eleve létező természeti elv, hanem maga is az univerzum evolúciója során jön létre. Tehát az univerzum korai szakaszában nincs is kvantum, ennek megszületéséhez idő kell. Létezik hát egy kvantum előtti és egy kvantum utáni korszak. Ezt a kvantumot az erős gravitáció hozza létre a tér mikro deformációja által. A mikro deformációk (részecskék) sokasága hozza létre a tér makro deformációját, azaz a szokásos gravitációt. Ez a felfogás eltér a modern fizika jelenlegi szemléletmódjától, amelyben minden erőt a kvantumokhoz és a kölcsönhatást közvetítő bozonokhoz próbálnak hozzárendelni. Nem véletlen, hogy ezt az elvet nem lehetett a gravitációra kiterjeszteni, mert a gravitáció a tér alapvető szerkezeti tulajdonsága, amihez nincs szükség „közvetítőkre”. Közvetíteni csak az erős gravitáció által stabilizált mikro deformációk (részecskék) között kell, amikor leírjuk átalakulásukat (gyenge kölcsönhatás) és a közöttük feszülő erőket (erős és elektromágneses kölcsönhatás ).

 A tér kezdeti kaotikusan lüktető szakaszában a rendezett forgások könnyen egymásba alakulnak, ekkor még a kvarkokat összekötő erős kölcsönhatás nem válik szét a forgási módok egymásba alakulásáért felelős gyenge kölcsönhatástól.  Ez a szétválás akkor következik be, amikor a kéttengelyű forgások is stabilizálódnak. Az egytengelyű forgások két típusa, amikor a haladási irány a forgási tengellyel párhuzamos (foton) és amikor merőleges (W és Z bozon), akkor válik szét, amikor elég sok fordulat következik be, hogy jól definiált forgási tengelyről lehessen beszélni.

Az anyag dominanciája az antianyaggal szemben

A jelenlegi ősrobbanás elmélet gyenge pontja, hogy nem tud meggyőző magyarázatot adni a részecskevilág fölényére az antirészecskékkel szemben. Ennek oka, hogy a párképződés során minden részecske az antirészecske párjával együtt képződik. Viszont ez a pár előbb-utóbb annihilál és fotonokat hoz létre. Ennek feloldást úgy magyarázhatjuk, hogy a kaotikusan lüktető és forgásszimmetriával és ezáltal kvantummal nem rendelkező térből alakulnak ki rendezett és kvantumos  forgások. A kvantumok születési folyamata már nem követeli meg ugyanazokat a kiválasztási szabályokat, amit a mai hideg, konszolidált univerzumunkban megfigyelhetünk a gammasugárzás párkeltése során. Emiatt a protonok kialakulhattak antiproton párjuk, illetve az elektronok pozitron nélkül is. Például a fiatal univerzumban létrejöhettek  proton-elektron párok és ugyanakkora valószínűséggel képződhettek antiproton-pozitron párok is, de a kétféle pár tényleges száma a véletlen törvényszerűsége miatt már nem volt azonos. (ezt a szcenáriót alátámasztja, hogy az univerzumot a pozitív és negatív töltések egyensúlya jellemzi). Végül valamelyik pár a kettő közül többségbe került és ez a többség az annihilációs folyamatok lezajlása után már fennmaradt. Ezt a többséget nevezzük ma anyagnak, amely uralkodik az antianyag felett.

A korai univerzum felfúvódása

Végül térjünk ki az ősrobbanás egy sajátos jelenségére, az inflációra vagy felfúvódásra is.  Az univerzum kora 13,7 milliárd év, viszont egyes csillagászati megfigyelések szerint a mérete a vártnál nagyobb, úgy 30 milliárd fényév. Ez csak úgy lehet, ha egyes korszakokban a fénysebességet meghaladó növekedésre került sor. Jelenleg úgy becsülik, hogy -35 és -30 LI között lehetett az a korszak, amikor a térfogat akár 50 nagyságrenddel is megnövekedhetett. De hogyan egyeztethető ez össze a speciális relativitáselmélettel? Ennek magyarázatához gondoljuk végig miért szükségszerű, hogy minden kölcsönhatás sebessége véges legyen. Például az elektromágnesesség és a gravitáció egyaránt c sebességgel terjed. De mi történne, ha minden kölcsönhatás késleltetés nélkül éreztetné hatását? Például az egyik galaxis valamit megváltoztatna a másikon, akkor ennek hatása késleltetés nélkül visszahatna az elsőre. Ez újra hatna a másikra és a hatások végtelen sora jönne létre. Ha ezáltal valami növekedne az egyik helyen, akkor a növekedések egy végtelen sok tagból álló és egynél nagyobb kvóciensű mértani sor összegének felelne meg, ami viszont végtelen lenne és a galaxisok felrobbannának. Csökkentést okozó kölcsönhatás esetén pedig az egynél kisebb kvóciens miatt mindkét galaxis eltűnne. Stabilis univerzum ezért csak úgy alakulhat ki, ha minden kölcsönhatás sebessége véges és ez jelenik meg a hatások véges c határsebességében. Az univerzum felfúvódása nem mond ellent ennek az elvnek, csupán az univerzum jobban szétszakad egymással kölcsönhatásba nem kerülő téridő tartományokra. Ugyanis ha tőlünk egymillió év távolában felrobban egy szupernóva, akkor az nem befolyásolja világunkat, mert hatása csak millió év múlva jelenik meg. Ez azt jelenti, hogy a téridő két tartománya között nincs kölcsönhatás. A felfúvódás miatt viszont megnövekszik az a téridőt tartomány, amellyel nem állunk kölcsönhatásban. Az univerzum stabilitását ez a jelenség tehát megerősíti. De mi azaz erő, ami előidézte a felfúvódást? A kérdés megválaszolásával még adós az ősrobbanás elmélete..

Az ősrobbanás elméletéhez kapcsolható mitológiák: Az ősrobbanás és a teremtészmítoszok_III

Az ősrobbanás és a teremtésmítoszok

Ennek a bejegyzésnek kettős célja van. Egyrészt az ókori ember gondolkozásmódját hasonlítom össze a modern kor tudományokra alapozott felfogásával, másrészt az ősrobbanás mai elméletét vetem össze a részecskék fénysebességű mozgásából származtatható kozmológiával. 

Miért jutottak a különböző kultúrák és vallások a világ teremtésének, keletkezésének gondolatához? Minden ember megszületik, él és meghal, ugyanez vonatkozik valamennyi állatra és növényre is. Az egyes kultúrák emlékezetében él, hogy voltak előző kultúrák is, amelyek létrejöttek, virágoztak majd a semmibe tűntek. Ezért már az ókori ember is úgy gondolkozott, hogy ezen a világon semmi sem örök, mindennek megvan a maga küldetése, mindennek egyszer vége szakad. De ez együtt jár avval, hogy mindennek egyszer meg kellett születni, teremtődni. Ha ez minden létezőre igaz, akkor igaznak kell lenni az egész világra is.

Mózes első könyve

De mi is ez a világ? Van a mi világunk, a földi világ és ami fölöttünk van az égi világ. Ez a kettőség a kiindulópontja a legtöbb teremtésmítosznak is. Idézzünk mindjárt Mózes első könyvéből:

1. Kezdetben teremté Isten az eget és a földet.
2. A föld pedig kietlen és puszta vala, és setétség vala a mélység színén, és az Isten Lelke lebeg vala a vizek felett.
3. És mondá Isten: Legyen világosság: és lőn világosság.
4. És látá Isten, hogy jó a világosság; és elválasztá Isten a világosságot a setétségtől.
5. És nevezé Isten a világosságot nappalnak, és a setétséget nevezé éjszakának: és lőn este és lőn reggel, első nap.

Az ókori ember természetesen a „föld” alatt nem a Földet mint bolygót értette, hanem az egész világot, amiben élünk. De életünk nagymértékben attól függ, ami fentről az „égből” érkezik, onnan kapjuk az éltető napsugarat és az esőt, de félhetünk a viharoktól, erős szelektől és a villámoktól is. Ez a felső függés jelenik meg a korai istenképekben is, gondoljunk a görög-római vagy az egyiptomi mitológiákra. Az istenkép fejlettebb, letisztult formája, amikor kialakul az egy-isten, a mindenható a teremtő tisztelete.

Az első lépés tehát az égi és földi világ megteremtése, és itt nem véletlen a sorrend. A földi világ önmagában halott, a sötétség uralja. Fontos, hogy amire először van szükség az a világosság, amit ma úgy mondunk, hogy a fény. Ez megelőzi a Nap és Hold megteremtését is, amire csak a negyedik napon kerül sor:

14. És mondá Isten: Legyenek világító testek az ég mennyezetén, hogy elválasszák a nappalt az éjszakától, és legyenek jelek, és meghatározói ünnepeknek, napoknak és esztendőknek.

15. És legyenek világítókul az ég mennyezetén hogy világítsanak a földre. És úgy lőn.

16. Teremté tehát Isten a két nagy világító testet, a nagyobbik világító testet, hogy uralkodjék nappal és a kisebbik világítótestet, hogy uralkodjék éjjel; és a csillagokat.

17. És helyezteté Isten azokat az ég mennyezetére, hogy világítsanak a földre;

18. És hogy uralkodjanak a nappalon és az éjszakán, és elválasszák a világosságot a setétségtől. És látá Isten, hogy jó.

19. És lőn este és lőn reggel, negyedik nap.

Érdekes egyezés, amint látni fogjuk a modern kozmológiában is, hogy előbb jött létre a fény, mint a nap a hold és a csillagok! Az ősrobbanás elmélete előtt még úgy gondolhattuk, hogy milyen naiv a biblia megközelítés, ami a csillagok megszületése elé helyezi a fény és világosság megteremtését. Ez figyelmeztetés számunkra: ne becsüljük le az ősi népek gondolatvilágát. Modern elméleteink bizony gyakran tökéletlenek, amit a távoli jövőben fognak majd naivnak tartani.

Minden élet számára kiemelt fontosságú a víz, ezért kerül a víz „szétválasztása” már előre, a második napra. A sorrend tehát azt tükrözi, hogy mit tartott az ókor embere a legfontosabbnak. Mivel az ősi kultúrák a forró és száraz övezetekben alakultak ki, például Mezopotámiában és Egyiptomban, ezért a víz, az eső megjelenése előre kerül:

6. És mondá Isten: Legyen mennyezet a víz között, a mely elválassza a vizeket a vizektől.
7. Teremté tehát Isten a mennyezetet, és elválasztá a mennyezet alatt való vizeket, a mennyezet felett való vizektől.
8. És nevezé Isten a mennyezetet égnek: és lőn este, és lőn reggel, második nap.
9. És mondá Isten: Gyűljetek egybe az ég alatt való vizek egy helyre, hogy tessék meg a száraz. És úgy lőn.  
10. És nevezé Isten a szárazat földnek; az egybegyült vizeket pedig tengernek nevezé. És látá Isten, hogy jó.

Az égi víz, az eső, ami a felhőkből („mennyezet") származik hozta létre a tengereket. Megint egy érdekes egyezés, ahogy ma magyarázzuk a Föld forró korszakának lehűlése után a tengereinek kialakulását. Természetesen nincs arról szó, hogy a bibliai teremtéstörténet mindenben azonos lenne avval a sorrenddel, amit ma elképzelünk, de érdekes módon azért a sorrend sokszor a fontosság mellett kapcsolatba hozható a Föld és az élet evolúciójáról alkotott elképzeléseinkkel is.

A Korán

Az iszlám teremtéstörténet sok hasonlóságot mutat a bibliával, ennek illusztrálására olvassunk el néhány sort a Koránból is:

Allah megparancsolta a víz felett lebegő párának, emelkedjék a magasba. És két nap alatt megalkotta az eget. Ezután elválasztotta az eget a földtől, és létrehozta a hét eget és a hét földet.

Amikor Allah megalkotta a földeket, megparancsolta a szélnek, hogy kavarja fel a vizet. A víz megmozdult, és tajtékzott, magas hullámok tornyosultak, és sűrű pára képződött. Allah elrendelte a tajtéknak: szilárduljon meg,  és a tajték megszilárdult. Ebből alkotta meg két nap alatt a víz színén a földeket. Ekkor megparancsolta a hullámoknak: álljanak meg. A hullámok megmeredtek, és ezekből alkotta Allah a hegyeket.

Mezopotámiai mitológia

A víz különös fontossága jelenik meg a mezopotámiai teremtéstörténetben is, nézzük az első táblát:

Midőn fönn az ég nevetlen s alant a föld szintazonképp;

Apszu, az ős-kezdet, minden dolgok teremtője-atyja

s Mummu-Tiámat ősanyánk még vizeikkel egybemosódtak;

nem volt szárazföld se, láp se, s egyike sem az isteneknek;

név nélkül szunnyadott a sors is, betöltetlen várt a végzet

Az ég és a föld egymásutánisága szintén megjelenik, és kiemelt szerepet kap a víz. Az ókori gondolkozás másik jellegzetessége, hogy a „teremtés” voltaképp nem más mint „megnevezés”, erre utalt a Mózes könyvéből vett idézet 10. sora is! A mezopotámiai mitológiában az egymást követő és egymással harcoló istenek sora felel meg a teremtés egymást követő lépéseinek. Marduk születése kapcsolódik a Naphoz, képviseli a nappalok és éjszakák kettőségét, valamint a négy évszakot és a négy égtájat is. Idézzünk fel néhány sort még e korai költészet remekművéből:

Midőn Éa, nemzőatyja reánéz, örvend és ujjong - megdobog a szíve.

Tökéletesnek teremté őt, kétfejűnek; méltóságban mindenki mást felülmúl;

tagjai tündöklőbbek az elégnél;alig-felfoghatók, hozzá-nem-férhetőek.

Szeme négy és füle is négy vala, szájából lángos tűz csapott elő;

négy füllel fülelt, négy szemmel tekintett - mindent látott és mindent hallott.

Sudárabb a nagy isteneknél, soraikból fejjel kimagaslik:

 tagjai fönségesen nőttek, másokéinál ékesebben.

"Miféle sarj, kinek a magva ez? Miféle sarj, kinek a magva ez?

Az Ifjú Napnak, a Tavaszi Napnak, az Istenek Napjának sarja ő!

Egyiptomi teremtéstörténet

Az egyiptomi teremtéstörténetben is a víz és a fény játssza az alapvető szerepet és a mezopotámiai istenmítoszokhoz hasonlóan ez is egy gyönyörű költői vízió:

Kezdetben nem volt sem ég, sem föld, sem élők, sem holtak nem voltak, az alkotó és romboló elemek is dermedt tétlenségben nyugodtak Nun isten örvénylő mélyén. Nun volt az őselem, az ősvíz formájában létező istenlény. Az ő alkotórészeiből keletkezett a mindenség. Az ősvíz tükrét sűrű sötétség borította, mert a fény szent forrása is Nun keblében pihent. És az istenek létrehozója, a hatalmas Nun megteremtette a napvilágot. Az ősvíz színén zsenge csíra bukkant elő, és hamarosan kecses, sok színben pompázó lótuszvirággá nőtt. A virág áttetsző, zárt kelyhéből sejtelmes fény derengett, szirmai lassan kibomlottak, és egy tündöklő gyermek bújt ki belőle. Nun életre keltette Nefertumot, a napgyermeket. Nefertum felnyitotta szemét, a sötétség eloszlott, s a világot beragyogta az éltető fény.

A virágbölcsőjéből kiemelkedő napgyermek körültekintett, s a végtelen vízen egy cseppnyi hely sem akadt, ahol lábát megvethette volna. Ekkor a mélyből előhívta az őshalmot. Kilépett a szilárd talajra, és megteremtette Maátot, a mindenség törvényét, az igazság istennőjét, a holtak szívének túlvilági bíráját.

Indiai teremtéstörténet

Költői szépségében nem marad el ettől az indiai teremtéstörténet sem, amelyben a „gondolat” hozza mozgásba a mozdulatlan és sötét világot:

A Világéjszaka sötét, mindent elborító, mozdulatlan tengerének színén összecsavarodva nyugodott Ananta, a Végtelenség Kígyója, s rajta álomba merülve pihent Visnu, a mindenség létesítője és fenntartója, az egyetlen hatalom. Bensejében a világ egész tartalma mint nyugvó gondolat derengett, rajta kívül nem volt élet, nem mozdult semmi. Álmában egyszerre megrezdült benne a gondolat, és Visnu felébredt. Kinyitotta szemét, és látott. Abban a szempillantásban megindult a mozgás az odáig nyugvó ősanyagban. Visnu létesítő akarata kisarjadt, és köldökéből egy lótusz nőtt elő. A lótusz széttárta szirmait, és íme, a lótusz kelyhében ült Brahmá, az Egynek Teremtő Ereje.

Brahmá körül akart tekinteni, de nem moccant meg. Hogy mindenfelé láthasson, négy arca keletkezett. A gyökeret azonban, amelyből létre fakadt, nem látta, s ezért azt gondolta, hogy egyedül ő van, kívüle nincsen öntudat. Csak a lótuszt látta, mely őt hordozta, s ez a lótusz a világmindenség volt. Gondolkozni kezdett: "Honnan származott ez a lótusz? Honnan jöttem én magam?" Hosszú-hosszú időkig elmélkedett e kérdéseken, míg végül a szívében, lénye legmélyén felderengett egy kép: a mindenség sötét vizén s a Végtelenség Kígyóján nyugvó Egynek, a Világ Gyökerének a képe.

Tibeti teremtéstörténet

A tibeti teremtéstörténet filozófiai mélységével alkotott maradandót:

Kezdetben semmi sem létezett, sem tér, sem idő, sem valóság, sem jel, sem lét, sem nemlét. Ebből keletkezett minden, ami látható és tapintható.

Az első lény varázslatos átalakulási képességgel született. Megnevezte magát: "A Keletkező Világ Ura, Szent Győzedelmeskedő". És boldog volt, mert hatalma mindenre kiterjedt.

Ekkor a négy évszak még nem vált el egymástól, a nap, a hold, a bolygók és a csillagképek alig mozdultak, a mennydörgés, a villámlás, az eső, a jég, a fagy sem követték az évszakok változásait. A földnek nem volt ura, az erdők, a növények maguktól nőttek és szaporodtak. A kövek és a hegyek már létrejöttek, de még nem mozdultak, és a földrengés is ismeretlen volt. A föld aranyból volt. A folyók is megvoltak már, de még nem indultak el a tenger felé. Madarak és vadak is éltek az erdőkben, de még senki sem vadászott rájuk. Istenek is léteztek, de még nem hallgatták meg a könyörgéseket, és nem uralkodtak ég és föld felett. Létrejöttek a démonok is, de még nem kezdhették el romboló munkájukat. Voltak betegségek, de még nem okoztak kínt és fájdalmat. Volt már táplálék, de még senki nem fogyasztotta. A boldogság is létezett, de nem volt, aki felfogja. A nappal nem különbözött az éjszakától.

Japán teremtéstörténet

A japán teremtéstörténet fő jellegzetessége, hogy nem egy nagy kontinensen, hanem néhány szigeten fejlődött ki ez a kultúra. Megjelenik a mítoszban a káosz is, mint a későbbi világ előképe. Ez a gondolat az alapja a modern kozmológiának is.

Abban az időben, amikor a föld és az ég keletkezett, a magas égi mezőkön három istenség lakozott. Az istenek maguktól születtek, majd elrejtőztek. Később a föld óriás olajcseppként lebegett a víz színén, és úgy mozgott fel s alá, mint egy roppant medúza. Ekkor a bambusznád csírájából két újabb isten támadt, de ezek is elrejtőztek, és számos utódnak adtak életet. E dicső leszármazottak sarja volt az istenek atyja és anyja, Izanagi és Izanami. Az istenek őket bízták meg, hogy megszilárdítsák és megtermékenyítsék a kocsonyás, mozgó földet.

Izanagi és Izanami letekintettek a Menny Lebegő Hídjáról, és azt fürkészték, van-e föld valahol a híd alatt. Csillogó drágakőből hatalmas lándzsát készítettek, a fegyvert lehajították, és rábukkantak a tengerre. Ezután kiemelték a lándzsát a káoszból, a káosz cseppenként aláhullott, megszilárdult, és így keletkezett Onokoro-Jima, a Megdermedt Sziget. Ezután még egy szigetet alkottak a tengerben, és leszálltak a földre.

A japán mitológiában a Napnak és a Holdnak is kiemelt szerepe van, amit a következő sorok mutatnak:

Ekkor megszülték a nap istennőjét, Amateraszut, akit a "nagy istenség éji fényessége" néven ismernek, és már születése után oly gyönyörű volt, hogy szülei nyomban felküldték a mennyei létrán, hogy az égről sugározza le a földre ragyogó fényét.

Következő gyermekük, Tsuki-jumi, a hold ura lett. Tsuki-jumi tompa, ezüstös csillogása elhalványult nővére arany pompája mellett, de azért méltónak mutatkozott arra, hogy Amateraszu hitvese legyen. Ő is felkapaszkodott az égi létrán, de hamarosan civakodni kezdtek. Amateraszu megelégelve az örökös egyenetlenséget, így szólt:

- Távolodj el tőlem, nem akarlak többé szemtől szembe látni.

Ekkor az istenek elválasztották őket, a házastársak szétköltöztek, és a nappal elvált az éjszakától.

Kínai teremtéstörténet

A kínai teremtésmitológia a Jin és Jang egymást kiegészítő ellentétpárjára épül és itt is megjelenik a káosz mint a világ kialakulásának kezdete:

Kezdetben, amikor az ég és a föld még tojás alakú káosz volt, Pan Ku megszületett a tojásban, és itt élt tizennyolcezer esztendeig. És ekkor a Jang tiszta elemeiből megformálódott az ég, a Jin durvább elemeiből pedig a föld. Pan Ku a középpontban tartózkodott, és nap mint nap kilenc alkalommal alakult át: hol az ég, hol pedig a föld istene volt. Az ég naponta három méterrel emelkedett magasabbra, a föld három méterrel vastagodott. Így folytatódott ez tizennyolcezer éven át, míg az ég elérte a legnagyobb magasságot, és a föld a legnagyobb mélységet.

Pan Ku az élet kezdete. Ő az őse tizennyolcezer élőlénynek. Amikor Pan Ku meghalt, fejéből szent szirt lett, szeméből a nap és a hold, zsírjából a folyók és a tengerek, hajából és szőréből a fák és a növények. Pan Ku könnyeiből fakadt a Sárga Folyó és a Kék Folyam. Hangja alkotta a mennydörgést, lehelete a szelet, pillantása a villámot; az ég kiderült, amikor Pan Ku vidám volt, a rosszkedvétől elborult. Pan Ku volt a Jang és felesége a Jin, a teremtés férfi és női eleme.

Maya teremtéstörténet

Nézzünk át Közép-Amerikába is, hogyan képzeték el a mayák a teremtést. Itt is szerepet játszik a gondolat és a szó teremtő ereje, a fény és a vizek szétválasztása a föld létrehozásában:

Elmélkedtek (az istenek), és íme, megvilágosodtak, megjelent az Ősfényhajnal, és terveikben megjelent az ember.

Ennek utána elgondolták a teremtést, elgondolták a fák és folyondárok növekedését, az élet születését és az ember alkotását és a sötétségben és fénytelen éjszakában ekképpen szerezte mindezt Égszíve, az, akit Hurakánnak mondanak...

Miképpen legyen élet, és miképpen jöjjön létre világosság? Kinek kell gondoskodnia táplálékról és betévő falatról?

- Jöjjön immár, és legyen! Népesüljön be az üresség!

- Húzódjanak félre a vizek, és hagyják el helyüket! Tűnjenek elő a szárazok, és szilárduljanak! Legyen!

Így szóltak.

- Legyen élet és legyen világosság az égen és a földön! És ne legyen ragyogás, nagyság és dicsőség művükben és teremtésünkben, míg nem alkottunk embert, míg testet nem öltött az ember!

Így szóltak. És utána megcselekedték és így megteremtették a földet. Igen, így volt, így teremtették a földet. Nem volt föld, és így szóltak:

- Föld! - És egy szempillantás alatt létrejött a föld...

Ekképpen teremtetett a föld, így teremtetett általa, kinek neve Égszíve és Földszíve, és aki termékennyé tette a földet, mikor még várakozás borult az égre, és víz borult a szárazra.

Afrikai legenda

Fejezzük be teremtéstörténeti kalandozásunkat egy afrikai legendával:

Ezt az apám mesélte el nekem, ő meg az apjától hallotta; réges-régtől fogva, a világ kezdetétől száll így ez a történet.

A dolgok kezdetén, mindennek az elején, mikor még semmi se volt, se ember, se állat, se növény, se ég, se föld, semmi, semmi, de semmi, csak az Isten volt, és úgy hívták, hogy: Nzamé. És három Nzamé volt: Nzamé, Mebere és Nkva. Kezdetben teremtette Nzamé az eget és a földet. Az eget magának tartotta fenn. A földre pedig rálehelt, és lehelete nyomán megszületett a szárazföld és a víz, mindkettő a maga helyén.

Nzamé mindent megteremtett: az eget, a napot, a holdat, a csillagokat, az állatokat, a növényeket, mindent, mindent.

Természetesen minden teremtéstörténet eljut az ember megteremtéséig, de mivel szándékunk a modern kozmológiával való összevetés, ezért a természet létrehozására vonatkozó motívumokat emeltük ki. A következő részben térünk rá a modern, tudományra alapozott mitológiára, az ősrobbanás elméletérre: Az ősrobbanás és a teremtésmítoszok_II