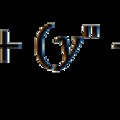A tér és idő fogalmának eredete
Az első részben már foglalkoztunk a téridő sajátságaival a kétréses kísérletek értelmezése során. Ott csak a kölcsönhatásban nem lévő fotonnal foglalkoztunk, itt most kibővítjük a redukált téridő fogalmát az elektronokra is. A redukált téridő a mikrovilág törvényeit határozza meg, a teljes téridő viszont a makroszkopikus világ értelmezési kereteit adja meg. Hétköznapi világunkban rengeteg információ ér minket, aminek hordozói elsősorban a fotonok, amelyek minden irányból és nagy távolságokból is szüntelenül érnek minket. Agyunk nagyszerű munkát végez, amikor összehasonlítja a különböző helyről érkező fotonok tulajdonságait és segít minket a tájékozódásban. Így alkotja meg azt a térfogalmat, ami jól elrendezi az információk sorát. Ebben az értelemben a tér fogalma, ami irányokból és távolságokból tevődik össze, jó összhangban van a kölcsönhatások terével, hiszen minden információ valamilyen kölcsönhatáshoz kapcsolódik. A másik fontos rendezési elv az idő, ami összegzi az események egymásutániságát, gyakoriságát, ismétlődéseit, valamint különbséget tesz az okok és a következmények között. Ahhoz már ki kell lépni a hétköznapi sebességek világból, hogy eljussunk a tér és idő fogalom összekapcsolásához, mert ennek hatása csak felfoghatatlanul nagy sebességeknél jelentkezik. Ezt az összekapcsolást alkotta meg a relativitáselmélet.
A mikrovilág pálya fogalma
A másik nagy ugrás fizikai szemléletünkben azáltal következett be, hogy műszereink segítségével közvetlen kapcsolatba kerülhettünk a mikrovilággal, melynek törvényeit a kvantummechanika fogalmazza meg. Az elmélet körüli értelmezési vitákat főleg az okozza, hogy az elmélet matematikai kidolgozását nem követte a fogalmi rendszer következetes átértelmezése. A klasszikus fizika pályafogalma ugyanis átalakult a valószínűség fogalmának színrelépésével. Úgy is fogalmazhatunk, hogy a stacionárius pályán már nem azt a kérdést tesszük fel, hogy az objektum mikor ér el a tér egy adott pontjához, hanem azt, hogy mekkora valószínűséggel található meg ott, következésképp a pálya fogalma nem mozgást, hanem állapotot fejez ki. (Lásd még „Az intelligens elektron” c. bejegyzést.) Ha a mérés során a részecskét a tér valamelyik pontjában detektáltuk, akkor megszűnik annak a lehetősége, hogy bárhol másutt legyen. Ez nem jelenti azt, hogy ezáltal a fénynél gyorsabb változást idéztünk elő, mert a valószínűségi dimenzióban történő leírás nem keverhető össze az idő dimenzión alapuló pályafogalommal. Mivel az idő helyébe a valószínűség dimenziója lépett, így helyesebb a mikrovilágban már nem is téridőről, hanem tér-valószínűségről beszélni, amikor kötött állapotról van szó. Itt lényeges a kötött állapot hangsúlyozása, mert az elektromágneses mezőben mozgó elektron, vagy ionizált részecskék esetében a pálya továbbra is az idő függvénye, az energia pedig, nem diszkréten, hanem folytonosan változik. Fontos különbséget tenni a kölcsönhatás különböző szerepei között, stacionárius állapotban a kölcsönhatás – például a töltött részecskék közötti Coulomb vonzás – fenntartja, míg kvantumugrások esetén megváltoztatja az állapotot. A klasszikus fizikában ez a különbségtétel nem lép fel.
Rejtett idő és fázis a kvantummechanikában
Vajon teljesen elvész az idő a stacionárius kvantumállapotban? Nem erről van szó, hanem arról, hogy amikor stacionárius állapotról beszélünk, akkor nem vagyunk kölcsönhatásban a vizsgált mikro-rendszerrel. Ha kapcsolatba lépünk vele, akkor ez már az állapot megváltozását jelenti. De még ez előtt is „történik” valami, ami előttünk rejtve van. Ahogy a fotonnak is van egy „belső órája”, amelyik állandóan változtatja a fázist, de ezt csak az interferencia jelenségek során észleljük, úgy az elektronok és más elemi részecskék „órája” is ketyeg, de erről nem tudhatunk, hiszen a stacionárius állapot a kölcsönhatás hiányát jelenti. Ennek tudomásulvételéről van szó a kvantumelektrodinamikában (lásd később), amikor a fotonokat és az elektronokat is oszcillációként írja le. Minden stacionárius állapotnak van valamekkora energiája, ami meghatározza az oszcillátor frekvenciáját, de mi sohasem ezt a frekvenciát látjuk, csak ennek megváltozását, amikor az elektron ugrást végez két állapot között. Ez a frekvencia igazgatja a fázis periodikus változását, aminek általunk ismeretlen értéke határozza meg, hogy mikor következik be az elektronugrás két állapot között. Mivel számunkra ez a fázis ismeretlen, így csak valószínűségi kijelentéseket tehetünk az állapotváltozás bekövetkezésére. Ezt a valószínűséget hívja a kvantummechanika átmeneti valószínűségnek. A kvantummechanika tehát egy „praktikus” elmélet, mert válaszol minden kérdésre, amit mérhetünk, de nem ad útmutatást az előttünk rejtve maradó folyamatokról.
A kölcsönhatások hierarchiája
Az atomok összetevőinek világáról csak műszerek által közvetített információink vannak, és az elemi részecskékre csak korlátozott számú és minőségű kölcsönhatás hat. Természetesen az utóbbi megállapítás közelítés, ami azon alapul, hogy az elemi részecskék között csak a közvetlen szomszédságtól érkező kölcsönhatásokat vesszük figyelembe. Tudjuk azonban, hogy elvben minden objektum kölcsönhatásban van a teljes fizikai világgal, de ha ebből indulunk ki, akkor megoldhatatlanul bonyolult feladattal találkozunk. Ezért van szükség a kölcsönhatások hierarchiájának megállapítására. Ebben a hierarchiában megkülönböztethetünk fokozatokat és lépésről lépésre közelíthetünk az egyre pontosabb leíráshoz, de a teljeset, a valóságosat sohasem érhetjük el.
A makroszkopikus információk szerepe a mikrovilág tulajdonságainak feltárásában
A mikrovilágról nyerhető információ jellegét az információ hordozójának, a fotonnak a tulajdonságai határolják be. Erről az előző részben már írtam. Most csak azt emelem ki, hogy valójában sohasem egyetlen elemi objektumról szerezhető információt dolgozunk fel, ezt mindig kiegészítjük makroszkopikus ismeretekkel. Követhetjük például egyetlen részecske útját az emulzióban, vagy a ködkamrában, de ekkor azért láthatjuk az ionizáló sugárzás nyomát, mert a nagy energiájú részecske mozgása során nagyszámú molekula szerkezetét változtatja meg, ami „nyomot” hagy. Erről a nyomról pedig nagyszámú foton ad hírt, amikor vizsgáljuk a részecske pályáját. Tehát amikor egyetlen részecske tulajdonságaira következtetünk, akkor hallgatólagosan felhasználjuk azt a tudást, amit a makroszkopikus világ nyújt számunkra. Ugyanez a helyzet a korábban tárgyalt kétréses kísérletben is, ahol a térről szerzett tudást a műszerről szerzett ismereteink biztosították. Amikor a foton, vagy egy elektron pályáját a kölcsönhatás előtti időszakban akarjuk jellemezni, nem állnak rendelkezésre térbeli irányok és távolságok, amihez hasonlítani tudnánk a mozgási pályát, arról sincs információnk, hogy épp hol tartózkodik a részecske. Viszont amikor a fotont, vagy elektront detektáljuk, akkor látjuk azt a helyet, ahol a kölcsönhatás megtörtént és tudhatjuk annak időpontját is. Ezek azonban makroszkopikus információk.
A kvantumelektrodinamika szemléletmódja
A kvantumelektrodinamika leírja a fotonok és elektronok állapotát, abban az időszakban is, amikor nincs még észlelhető kölcsönhatás. A leírásban a szokásos (makroszkopikus) tér és idő fogalmát használjuk. Ennek elmélete a kvantumelektrodinamika, melyben a fotonok és elektronok együttes rendszerét vizsgáljuk, ahol a mozgásokat és kölcsönhatásokat a foton és elektronok számának változásával jellemezzük. Ez a mezőelméleti megközelítés alkalmasabb a mikro-rendszer állapotának és folyamatainak leírására, mint az elektronok állapotát önmagában vizsgáló kvantummechanika, mert itt a fotonok a kvantumfolyamatok egyenrangú résztvevőivé válnak. A módszer sajátsága, hogy a fotonokhoz és elektronokhoz egyaránt oszcillációkat rendel. Az általam javasolt fénysebességű forgásmodellel ez teljes összhangban van, mert a forgások vetületi képei oszcillációnak felelnek meg. A ténylegesen kibocsátott és elnyelt fotonokon kívül a mezőelmélet virtuális fotonokról is beszél, melyek szerepe a töltött részecskék (például az atommag és az elektronok) közötti elektromos és mágneses mező létrehozása. A legkülönösebb az elméletben, hogy megenged fénynél sebesebb mozgásokat, virtuálisan létrejövő elektron-pozitron párokat, sőt az idő megfordulását is, amikor előbb veszi figyelembe az elektron-pozitron pár hatását, mint amikor létrejött. A furcsa jelenségek oka, hogy a kölcsönhatás előtti állapotban a tér és idő fiktív matematikai dimenzió, így minden lehetséges folyamat megengedett, sőt szükséges, amit csak a matematikai feltételek megkívánnak.
A redukált téridő
A kölcsönhatás nélküli eset fiktív térideje és a makroszkopikus téridő a két végletet képviseli, az utóbbit nevezhetjük a teljes téridőnek. Az atomok és molekulák leírásában bevezethetjük a redukált téridő fogalmát, amikor az elektromágneses kölcsönhatásokat figyelembe vesszük, melyek aztán információt adnak a tér szerkezetéről. Másképp fogalmazva, az elektronok teréről csak annyi információnk van, amennyit az elektronok kölcsönhatásai nyújtanak. Ennek első példája legyen a hidrogén atom, ahol egyetlen elektron „kering” (pontosabban tartózkodik) a proton körül. Ekkor az elektromos mező kizárólag a proton és elektron távolságától függ, az irányok között pedig nem lehet különbséget tenni. Ennek leírásához két módszert használhatunk. Ha a szokásos teljes téridővel írjuk le a mikro-állapotot, akkor az állapotot jellemző függvényben minden irányhoz azonos valószínűségi amplitúdót kell rendelni (a valószínűséget az amplitúdó abszolút értékének négyzete adja meg a kvantummechanikában). De bevezethetjük a redukált tér fogalmát is, amikor a teret csak az elektron-mag távolság jellemzi (ez a radiális paraméter) és nem szerepel benne az irány. A két felfogás között a kvantummechanika hidat teremt, mert bevezeti a szuperpozíció fogalmát. Ez azt jelenti, hogy az állapotfüggvény a különböző irányokhoz tartozó állapotok szuperpozíciója. Az egyes állapotokat két kvantumszámmal lehet jellemezni, melyek közül az első a radiális eloszlás maximum helyeinek számát, a másik pedig az impulzusnyomaték nagyságát adja meg (lásd „Miért diszkrétek az energiaállapotok kötött állapotban I-V). Vannak olyan állapotok, melyben az impulzusnyomaték nulla (ezeket nevezik s pályáknak), ekkor az impulzus mindig a centrum felé mutat, vagy avval épp ellentétes irányú, ami a centrumon áthaladó lineáris oszcilláció pályájának felel meg. Az s pálya ezeknek a lineáris oszcillációknak a szuperpozíciója. Tehát a gömbszimmetrikus s pálya nem azt jelenti, hogy a mozgás során az elektron minden irányba eljut, hanem arról van szó, hogy az irány fogalmának hiánya miatt minden irányban azonos valószínűség jellemzi a mikro-állapotot.
Impulzusnyomaték és az atomi pályák
Az elektron olyan pályákon is tartózkodhat, ahol az impulzusnyomaték nem nulla, például lehet ℏ (p pályák), vagy 2ℏ (d pályák) is. A pályacsaládok függvényeit a forgatások átviszik egymásba, a független pályák száma három a p és öt a d pályák esetében. Az irányok definiálatlansága abban nyilvánul meg, hogy az említett függvényterekben nincs kitüntetett pálya, egyenértékű bármelyik szuperpozíció, amennyiben az amplitúdók négyzeteinek összege kiadja az egységnyi, tehát a teljes valószínűséget. Ezek a pályák elkerülik a centrumot és egymástól elhatárolt valószínűségi tartományokból állnak, ahol a határokon nulla a valószínűség. A klasszikus gondolkodás felveti a kérdést, hogyan közlekedhet két tartomány között az elektron, ha az átmeneti régióban egyáltalán nem lehet? Tipikus kérdés, ami hibásan keveri a klasszikus és kvantumfogalmakat. Az elektronnak nem kell „közlekedni” a tartományok között, mert a pálya nem időbeli, hanem a valószínűség dimenziójában felépülő fizikai entitás.
Elektronpályák a molekulákban
Lépjünk tovább a molekulák világába és vizsgáljuk például a metán molekulában a szénatomban lévő elektronokat. Milyen lesz a redukált tér fogalma, amit az elektronok érzékelnek? Mivel a szén atommagján kívül az elektromos mezőt a tetraéder négy csúcsán levő hidrogénatomok is befolyásolják, a tetraéder csúcsainak iránya kitüntetett lesz. Más szóval bővül a redukált tér fogalma, amivel az elektronpályákat leírjuk, de még nem lesz teljes. Ennek oka, hogy nem tehetünk különbséget a négy hidrogén atom között. Matematikailag ezt a csoportelmélet segítségével vehetjük figyelembe, támaszkodva a tetraéder összes szimmetriaműveletére, aminek segítségével meghatározhatjuk a szuperpozíciós együtthatókat (valószínűségi amplitúdókat), amelyekkel szorozni kell az egyes s, p, d függvényeket, hogy felépítsük az elektronpályát. A számításban először csak a legerősebb kölcsönhatással foglalkozunk az elektronok és a szén atommag között, ezt egészítjük ki második lépésben az elektronok közötti kölcsönhatással, majd a harmadik lépésben kerül sor a hidrogén atomok perturbáló hatására. Ez felel meg annak, hogy a tér fogalmát bővítjük ki lépésről lépésre. Nagy molekuláknál, ahol már nincs geometriai szimmetria, a mikro-rendszer térfogalma már azonos lesz a makroszkopikussal, mert minden térirányban különbözik az elektromos mező. Még ebben az esetben is fennmarad egy szimmetria, ami az elektronok megkülönböztethetetlenségéből következik. Emiatt az elektronpályákat permutálni kell (determináns hullámfüggvény), és különböző matematikai közelítő eljárások révén lehet meghatározni az elektronok egész molekulára kiterjedő pályafüggvényeit. Nem célom az eljárások bemutatása, csak azt akarom kihangsúlyozni, hogy az elektronok nem lokalizálódnak az egyes atomokban, sőt kémiai kötésekben sem, hanem kiterjednek az egész molekulára. A mikrovilágban minden, ami megkülönböztethetetlen a kvantummechanikában mint szuperpozíció jelenik meg, és ezért lesz az elektron molekulapályája az egyes atompályák szuperpozíciója.
Záró gondolatok
A kvantummechanika különös szemléletmódja két alapvető okra vezethető vissza, amelyeket különböző példákon mutattam be négy részletben. Az egyik ok a foton szerkezetéből fakad, a fotonok által nyújtott információ korlátozott, mert a hullámhosszra és az impulzusra, illetve a frekvenciára és az energiára vonatkozó szabályok össze vannak kötve a Planck állandó és a fénysebesség állandósága miatt. A másik fontos tulajdonság, hogy minden foton azonos impulzusnyomatékkal rendelkezik, amely szintén a Planck állandóval egyezik meg. A kvantummechanika másik sajátsága, hogy a mikro-rendszereket, például az elektront magában foglaló térről csak annyit tudhatunk meg, amennyit a ráható kölcsönhatások szimmetriája megenged. Ehhez járul még az elektronok megkülönböztethetetlensége.
Az idő látszólag elvész, amikor stacionárius állapotról beszélünk, de rejtve mégis jelen a fázis formájában, ami majd akkor ad életjelet magáról, ha a stacionárius állapot megváltozik. Ez a jelenség okozza, hogy az átmenetek bekövetkezésének ideje helyett, csak annak valószínűségét mondhatjuk meg. Ez okozza a determinizmus hiányát a mikro-folyamatokban, ami azonban látszólagos, csupán a fázis értékének ismeretlenségét tükrözi.
Ezek a tulajdonságok jelennek meg a kvantummechanikában, melyben a fizikai mennyiségek operátorai, mint hatások jelennek meg, melyek vagy fenntartják, vagy megváltoztatják a mikro-rendszer állapotát. Ha szem előtt tartjuk ezeket az elveket, akkor közelebb juthatunk a mikrovilág rejtélyeinek megértéséhez.
További írások elérhetők: Paradigmaváltás a fizikában...