Növekvő számú elemi részecskék felfedezése

Univerzumunk alapvető építőkövei az atommagokat alkotó protonok és neutronok és az atomokban, molekulákban az atommagot körülvevő elektronok. Amíg csak ezeket a részecskéket ismerte a fizika, addig a mikrovilág felépítése egyszerűnek tűnt, mert az atomok teljes periódusos rendszere leírható volt ezekkel a részecskékkel, és az atommagok bomlása és fúziója is evvel magyarázhatóvá vált. A kísérleti technika továbbfejlődése és egyre nagyobb teljesítményű gyorsítók készítése azonban újabb és újabb részecskék felfedezésére vezetett. Először a pozitronok, majd később a neutrínók felfedezése még segített tisztázni eligazodásunkat a mikrovilágban, de később újabb és újabb részecskéket sikerült kimutatni az egyre nagyobb energiájú tartományokban az egyre rövidebb élettartamú mikrorészecskék megfigyelésével, ami már komoly gondot okozott eligazodni a világnak ebben a különös tartományában. A részecskék száma gyorsan növekedett és ma már jóval száz fölött jár. Evvel párhuzamosan nőtt az igény egy új rendezőelv megtalálására, amely rendet teremthet az elemi részecskék dzsungelében.

A törttöltésű elemi részecskék

Ezt a rendező elvet vetette fel Murray Gell-Mann és George Zweig 1964-ben, amelynek alapja a törttöltésű részecskék feltételezése volt, ahol is a töltés az elektron töltését alapul véve  ±2/3e illetve ±1/3e értéket vesz fel.  Ehhez a feltételezéshez azonban rendkívüli kutatói bátorság kellett, mert minden addigi – sőt azóta is elvégzett vizsgálat szerint –  csak  olyan elemi részecskéket lehetett kísérletileg kimutatni, amelynek elektromos töltése az elektron, illetve proton töltésének egészszámú többszöröse.  Ez ugyanolyan forradalmat indított el a fizikában, mint a XX. század elején Niels Bohr, aki az atom szerkezetének magyarázata érdekében az elektrodinamika egyik alaptételét felrúgva vetette fel, hogy az atommag körül keringő elektronok a gyorsuló mozgás ellenére sem bocsátanak ki elektromágneses sugárzást.  Ez vezetett annak idején a kvantummechanika kialakulásához, ami mára a mikrovilág értelmezésének alapja lett.

Valódi részecske-e a kvark?

Mivel törttöltésű részecskéket nem lehetett kísérletileg kimutatni (a később elfogadott kvarknak elnevezés James Joyce regényéből, a Finnegen ébredésében szereplő egyik mondatból származik), felvethető a kérdés, vajon a kvark tekinthető-e valóban létező fizikai objektumnak, vagy csupán egy olyan rendezőelv, ami segít osztályozni a mikrovilág legparányibb objektumait, az elemi részecskék világát?  Ebben a bejegyzésben úgy közelítem meg a kérdést, hogy választ keresek arra, miért nem lehet kísérletileg észlelni a kvarkokat. Ehhez ismét onnan indulok el, mint az előző részben, ahol a neutrínók oszcillációját magyaráztam a relativitáselmélet kovarianciájából, ami alapja valamennyi részecske elektromágneses kölcsönhatásának, és amely alapegyenletet neveztem el  mint általános fermion egyenletet.

Kvarkok a Standard Modellben

Tekintsük át röviden, hogy jelenlegi ismereteinket összegző Standard Modell mit is mond a kvarkokról. Mivel a kvarkokat nem tudjuk közvetlenül kimutatni, így minden tulajdonságát az észlelhető részecskékre vezetjük vissza, amelyeket a kvarkok felépítenek. Itt először is az „elemi részecske” fogalmát kell tisztázni, hiszen többé nem tekinthetjük ezeket a fizikai objektumokat valóban eleminek, ha tovább bontjuk még parányibb összetevőkre. Annak idején jogosan neveztük elemi részecskének a protont és a neutront, amiből felépülnek az atommagok, mert akkor még nem merülhetett fel az, hogy ezek az objektumok is felbonthatók.  Bár közvetlenül nem láthatjuk a kvarkokat a proton és neutron összetett jellege mégis kísérleti tény, mert nagyenergiájú ütközési és szóráskísérletek szerint töltésük térben kiterjedt inhomogén struktúrával rendelkezik, eltérően az elektrontól, amely hasonló kísérletekben pontszerűnek mutatkozik. Ezért az elektront és társait, nevezetesen az anti-részecskéjét, a pozitront, valamint az elektron „nagytestvéreit” a müont és a tau részecskét továbbra is valóban eleminek tekintjük. Úgyszintén elemi a neutrínó, ami az elektron típusú részecskékkel együtt alkotja a Standard Modellben a leptonok családját.

Az elemi részecskék osztályozásának elvei

A Standard Modell három alapvető elv alapján osztályozza az „összetett” elemi részecskéket (léteznek további osztályozási szempontok is, de itt csak a mondanivalónk szempontjából a legfontosabbakra térek ki:

• Mekkora a spinjük, azaz a részecskék saját impulzusnyomatéka. Az egyik típusba tartoznak a mezonok, ahol a spin 0 vagy 1 lehet. Ezek a részecskék a bozonokhoz tartoznak. A másik típus a fermionoké, ahol a spin ½ és 3/2 lehet. Ezeket nevezzük barionok A barionokat és a mezonokat együtt hadronoknak nevezi a szakirodalom.
• Mekkora a töltésük. A mezonoké 0, vagy ±e, a barionoké 0, ±e és ±2e
• A részecske és anti-részecske megkülönböztetése. Minden részecskének van anti-részecske párja, az utóbbi töltése mindig ellentétes az előbbivel. Az antiproton töltése –e, a protoné +e. A semleges neutronnak is van anti-részecskéje, amely szintén semleges. A neutron és antineutron ütközéskor megsemmisíti egymást gamma sugárzás kibocsátásával. Egész univerzumunk nagy aszimmetriája a részecskék fölénye az anti-részecskék felett. Ez az univerzum létezésének alapfeltétele, hiszen ha azonos számban léteznének a részecskék és anti-részecskék, akkor az univerzum gamma sugárzásban semmisülne meg.

A kvarkok mint fermionok

A kvarkok alapdefiníciója, hogy ½ spínű fermionok. Ebből már sok minden következik.  Emiatt a 3/2 spínű barionok három kvarkból épülnek fel. Az egységes felépítési elv szerint ez a proton és neutron esetén is három kvarkot jelent, ami úgy adhatja ki a proton +e és a neutron 0 töltését, ha létezik egy részecske +2/3e töltéssel , ezt nevezzük u (up) kvarknak és egy -1/3e töltéssel, ezt nevezzük d (down)-nak, amikor is az összetétel protonnál uud,  neutronnál udd. Ennek megfelelően az antiprotont az uud, az antineutront udd antikvark kombináció építi fel. A barionok családjában azonban léteznek a protonnal és neutronnal azonos tulajdonságú (spínű és töltésű) részecskék is, ami úgy értelmezhető, ha az elektronhoz hasonlóan a kvarkoknak is vannak nehezebb „testvérei” illetve „generációi”. Az u nak pédául a c (charm) és a t (top), a d-nek az s (strange) és a b (bottom). Ugyanez vonatkozik az u és a d antikvarkra is.

A Pauli elv és a szín-kvantumszám

A barionok családjában azonban létezik 3/2 spínű és +2e töltésű részecske is, amit az uuu kombináció hozhat létre.  A fermionokra azonban létezik egy nagyon fontos kizárási elv, amit Pauli fogalmazott meg: a fermionok csak olyan kombinációkat hozhatnak létre, amelybe minden egyes fermion „megkülönböztethető’, ez az elv megengedi az uu kombinációt, mert az u kvarkok két spin vetülettel rendelkeznek (+1/2 és -1/2), de uuu struktúra nem jöhet létre. Ezt oldja fel, ha a kvarkok rendelkeznek egy további tulajdonsággal, amit szín-kvantumszámnak neveztek el, amelyik három különböző értéket vehet fel analógiában a három alapszínnel (piros, kék és zöld). Ahogy a három szín együttese fehér lesz, úgy ha a három szín-kvantumszám mindegyike együtt van, akkor az eredő kvantumszám már nulla lesz. Ez azt jelenti, hogy a szín-kvantumszám kizárólag a kvarkokra jellemző, míg bármely barion (sőt mezon) nem rendelkezik evvel a tulajdonsággal.  Ehhez kapcsolódik a színtöltés fogalma, amely a kvarkok közötti erőskölcsönhatásban hasonló szerepet játszik, mint az elektromágneses kölcsönhatásban az elektromos töltés. A szín-kvantumszám alapvető szerepet játszik az erős kölcsönhatás elméletében, amit a kvantumelektrodinamika mintájára a kvantumkromodinamika ír le, ahol a fotonok szerepét a gluonok veszik át.

Nem beszéltünk még a mezonok kvarkszerkezetéről. Az 1 és 0 spint két kvark (pontosabban egy kvark és egy antikvark) kombinációja hozza létre, hasonlóan a töltésük is így értelmezhető. Az elmondottak lényege, hogy a kvarkok három generációja képes értelmezni az összes eddig detektált mezont és bariont, sőt előre vetítette olyan részecskék létezését, amit utólag sikerült kísérletileg is kimutatni.

Szabad kvarkok és a bezártsági elv

Az elméletnek azonban nem sikerült igazán meggyőző magyarázatot adni arra kérdésre, hogy miért nem lehet detektálni szabad kvarkokat. A nagyenergiájú gyorsítókban több mint két nagyságrenddel nagyobb energiájú ütközéseket lehet létrehozni a töltött részecskék között, mint azok nyugalmi tömege (lásd például az LHC kísérleteket), de kvarkot az óriási számú adat feldolgozása után sem lehetett találni. A kozmikus sugárzás ütközéseit is hiába vizsgálták, ahol a nukleonok nyugalmi energiájának akár tízezerszerese is előfordul, de szabad kvarkot itt sem lehetett felfedezni. A kvarkok hiányát a „bezártsági” elvvel próbálják magyarázni, de véleményem szerint a magyarázat nagyon erőltetett. Feltételezik, hogy a barionokban és a mezonokban a kvarkok közötti vonzóerő a távolsággal növekszik és akkora értéket vehet fel, amit egyetlen az univerzumban létező részecskeütközés sem képes legyőzni. Azért gondolom, hogy ez a magyarázat nem állja meg a helyét, mert ekkor a kvarkokat összekötő energia sok-sok nagyságrenddel  haladná meg a kvarkokból képződő hadronok nyugalmi energiáját. A magyarázatot ezért máshol keresem: olyan következtetésekből, amely a relativisztikus kovariancia elvből és a kvantummechanika alaptermészetévből fakad. Ezt fejtem ki a továbbiakban.

Relativisztikus kovariancia, a töltés és tömeg mint operátor

Az előző bejegyzésben (Hogyan oszcillálnak a nulla nyugalmi tömegű neutrínók?) mutattam be, hogyan alkotható meg a relativisztikus kovariancia elvből egy olyan alapegyenlet, amely egyaránt alkalmazható valamennyi elemi fermionra. A módszer Dirac felbontási technikájának továbbvitelén alapul, amikor a négydimenziós spinorok helyett nyolcdimenziós spinorokat alkalmaztam. A nyolcdimenziós teret három két-két dimenziós tér direktszorzatára felbontva vezettem be a töltés, a tömeg és az impulzus Pauli mátrixokkal definiált kvantummechanikai operátorait:

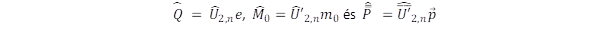
ahol az U_2,n unitér operátor a diagonális σ_z és a nem-diagonális σ_x Pauli mátrixból épül fel:

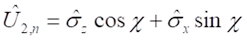
illetve 

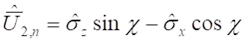
Az n részecske kvantumszám határozza meg a χ szöget, amelynek értéke 3, 2, 1 és 0 lehet és definiálja az elektron-pozitron párt, az up-antiup, a down-antidown kvarkokat, valamint a neutrínót:

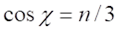
Az állapotfüggvény redukciója a részecskedetektálás során

Az n = 2 eset felel meg az u kvarknak, amikor is a töltés operátor diagonális eleme részecske állapotban 2/3e, míg anti-részecske állapotban -2/3e lesz. A d kvark töltését viszont az n = 1 kvantumszám határozza meg a ±1/3e diagonális elemek által.

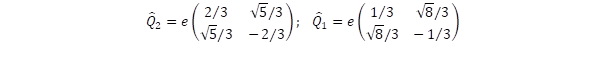
A töltés operátor nem-diagonális elemei miatt azonban a részecske nincs töltés sajátállapotban, azaz a tört töltés csupán a töltés várhatóértékét jelenti és a töltés valószínűség eloszlással jellemezhető. Ugyanez vonatkozik a nyugalmi tömegre és az impulzusra is.

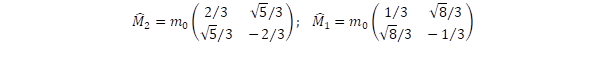
Tehát a részecske valamennyi fizikai paraméterét csak valószínűségi eloszlással jellemezhetjük. Amíg a mérés előtt – ez esetben a részecskedetektálás előtt – a hullámfüggvény valószínűség eloszlással jellemzi az objektum fizikai mennyiségeit, addig a mérés után már egy jól definiált értéket kapunk. Ezt nevezi a kvantummechanika irodalma a hullámfüggvény redukciójának. Ez a redukció megy végbe, amikor egy részecskét azonosítunk, ez a redukció tehát jól definiált töltés és tömeg megjelenésével jár együtt, azaz a mérés olyan kvantummechanikai állapotot hoz létre, amelyben a töltés és tömeg sajátállapotba kerül. Mivel a kvarkok nem lehetnek sem töltés, sem tömeg sajátállapotban, így detektálni sem lehet ezeket a részecskéket.

A kvarkok mint hadron mintázatok

                Lehet-e a kvarkokat önálló fizikai objektumoknak, részecskéknek tekinteni? Csak korlátozottan, mert létezésük a hadronok belsejére korlátozódik. Úgy foghatjuk fel, mint a hadronok azonos szerkezetű belső mintázatát. Ezt a mintázatot azonban nem lehet „kivágni” a hadronok belsejéből, mert az ott uralkodó kölcsönhatások hozzák létre ezeket a strukturális elemeket.

A fermion egyenlet tanulságai

                Az általános fermion egyenlettel egyaránt értelmezni tudunk két fontos jelenséget: egyrészt a neutrínó oszcillációra kapunk magyarázatot, másrészt érthetővé válik, hogy miért nem detektálhatunk olyan részecskét, amelynek tört töltése van.  Érdemes még kitérni arra, hogy miért csak renormált és nem mérhető tömege van a kvarkoknak. Ez szintén a tömeg operátor nem-diagonális jellegéből fakad.

A fizika kalandja blog további bejegyzéseinek összefoglalóját a megfelelő linkekkel együtt: lásd „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”