Einstein általános gravitációs elméletének egyik izgalmas következménye a fekete lyukak létezése, amit később a csillagászati megfigyelések fényesen igazoltak. De valóban csak Einstein elméletéből következik, hogy léteznek fekete lyukak?

Newton egyenlet

Induljunk ki Newton gravitációs egyenletéből, amivel értelmezni lehet a bolygókeringés törvényeit. Ha a bolygó tömege nagyon kicsi a Naphoz képest és körpályákra szorítkozunk, akkor a centrifugális erőt egyensúlyban tartó gravitációs erő:

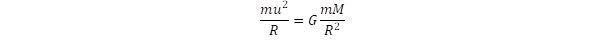
Az egyenlet egyik oldalán szerepel a tehetetlen tömeg, a másikon a gravitáló tömeg. A kettő egyenlősége miatt az egyenlőségből az m tömeg kiesik, és azt kapjuk, hogy

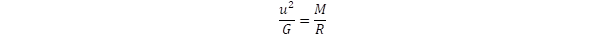
A sebességet meghatározó összefüggés ezért alkalmazható bármilyen kicsi is legyen a keringő tömeg, vonatkozik ez a fényre is, annál is inkább, mert az m = E/c² összefüggés szerint a fotonhoz is rendelhető mozgási tömeg. A foton viszont fénysebességgel mozog, ezért akkor kerül „kötött” pályára az M tömeg körül, ha

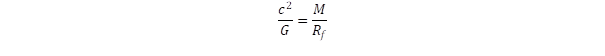
Itt a fénysebesség c = 3x10⁸ m/s és a gravitációs állandó G = 6,673x10^-11 m³/kg×s². (A relativitáselméletben a 2R_f sugár felel meg az eseményhorizontnak, mert ennél az értéknél az Einstein egyenletnek szingularitása van. Ez a kettes faktor a további meggondolások alapjait azonban nem érinti.)

Van egy másik feltétele is a fekete lyuk kialakulásának, mert az M tömeget magába záró objektum R_M sugara nem lehet nagyobb, mint a kötött foton pályasugara, azaz

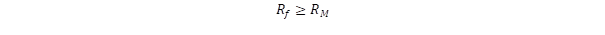
A feltételek teljesüléséhez nem csak extrém nagy tömegsűrűség kell, hanem megfelelő méret is. Azonos sűrűségű égitesteknél azért kedvezőbb a nagyobb méret a fekete lyuk kialakulásához, mert a tömeg R_M harmadik hatványával növekszik, míg az R_f pályasugár arányos a tömeggel.

Milyen csillagok lehetnek fekete lyukak?

Nézzük meg a feltételek teljesülését különböző égitesteknél! A Föld esetén a csapdázott foton pályasugara kisebb, mint 5 milliméter, a Napnál pedig 1,5 km körül van, ami jóval kisebb az égitestek kiterjedésénél. A Földre vagy Napba érkező fényt ezért nem a gravitáció fogja foglyul ejteni, hanem az égitestek felületen nyelődik el, és az égitestek felszínéről kibocsátott fénysugarak zavartalanul távozhatnak. A galaktika óriáscsillagai sem viselkedhetnek fekete lyukként, mert a tömegükhöz tartozó pályasugár nem haladja meg a 200 kilométert, amelynél saját sugaruk sok nagyságrenddel nagyobb.  A fekete lyukhoz szükséges nagy sűrűséget sokkal inkább a neutroncsillagoktól várhatjuk. Ezeknek tömege 1 és 3 Naptömeg között változik és sugaruk 10 km körül van. Egy közepes neutroncsillag 3x10³⁰ kg tömegét alapul véve a sűrűség 6x10¹⁷ kg/m³-nek adódik, míg a kötött foton pályasugara 2,5 km körül lehet. Ebből látható, hogy a 10 km sugarú neutroncsillagok sem viselkednek fekete test gyanánt.

A nukleonok tömegsűrűsége

Mielőtt továbblépnénk, érdemes elgondolkozni rajta, hogy mi határozza meg a neutroncsillagok, illetve a fekete testek tömegsűrűségét. Induljunk ki a nukleonokból, a protonból és neutronból. A szóráskísérletek szerint a proton sugara r_p = 0,87x10^-15 m, tömege pedig m_p = 1,66x10^-27 kg, az ebből számolható sűrűség ρ_p = 6x10¹⁷ kg/m³, egyezően a neutroncsillagoknál becsült értékkel. Tehát a neutroncsillag olyan mint egy sűrűn pakolt hatalmas neutron tömb! Érdemes azt is megjegyezni, hogy ez a sűrűség meghaladja a nagyobb atommagok sűrűségét, ami 3x10¹⁷ kg/m³ körül van. A Standard Modell szerint egyaránt az erős kölcsönhatás tartja egyben a kvarkokat a nukleonokban, és a nukleonokat az atommagokban. A sűrűség csökkenése nagyobb atommagoknál részben az erős kölcsönhatás rövid hatótávolságának, részben a protonok közötti elektrosztatikus taszításnak tulajdonítható.

Egy kis kémia

Az atommagok szerkezetének megismeréséhez segít, ha párhuzamot vonunk az atomi elektronpályákkal. Az elektronok héjakba rendeződnek, mert a spinhez két, az L impulzusmomentumhoz 2L +1 azonos energiájú pálya tartozik, és a Pauli elv szerint minden pályán csak egyetlen elektron lehet. Ez vezet a molekulák kialakulásához, mert az egyik atom zárt héja feletti többletelektronját átadhatja egy másik atomnak, ahol a héjból egy elektron hiányzik, ez az ionos kötés.  Ennél sokkal fontosabb azonban a kovalens kötés, ahol az atomok „megosztoznak” az elektronokon kölcsönösen kialakítva zárt héjakat. Ennek „nagymestere” a szén, amelynek vegyértékhéja félig van tele, azaz félig üres, és ebből fakad, hogy a szerves vegyületek végtelen sokasága jön létre.

Egy kis magfizika

Az atommagot alkotó protonok és neutronok is héjakba rendeződnek, de itt nagyságrendekkel nagyobb az energia és sokkal kisebb a nukleonok közötti távolság. Erre szükség is van, mert az erős kölcsönhatásnak rövid a hatótávolsága. Az atomok szerkezetének kialakításában három erő: az erős- és gyengekölcsönhatás, valamint az elektromágneses erő összjátékára van szükség. Az erős kölcsönhatás nem tesz különbséget a nukleonok között, egyforma erővel köt össze két protont, két neutront, vagy egy protont és egy neutront. De akkor miért nem jönnek létre már normál körülményeink között is neutron agglomerátumok, hiszen ekkor nem kellene legyőzni a töltések miatti taszító erőt! Itt lép be a gyenge kölcsönhatás, amely negyedóránként alakítja át a neutront protonná és így a tiszta neutronból felépülő tömbök nem stabilak. A neutront és protont is tartalmazó atommagokban a gyenge-kölcsönhatás már nem végzi el az átalakítást, mert a protonok számának növekedése egyrészt erősebb taszítást okoz, másrészt a proton is magasabb energiájú pályára kerülhet. A legstabilabb, azaz a legnagyobb kötési energiával rendelkező atommagokban, ilyen a hélium a neutronok és protonok, egyaránt betöltött pályán helyezkednek el. Ha az atommagban a nukleonok száma n, akkor közöttük n(n-1)/2 pár alakul ki, amivel arányosan növekszik az erős kölcsönhatás hozadéka. Ezért lesz a kötési energia egyre nagyobb az ⁵⁶Fe izotópig bezárólag. Ha ennél is nagyobb a nukleonok száma, akkor már gyarapszik az olyan „távoli” párok száma, amelyek között nincs erős-kölcsönhatás, és ráadásul a nagyobb protonszám növeli az elektrosztatikus taszítást, hiszen ez a kölcsönhatás alig csökken a nukleonok közötti távolsággal. Emiatt válnak bomlékonnyá az olyan atommagok, ahol a protonok száma már közelít százhoz.

A neutroncsillagok fizikája

A neutroncsillagokban már egy új játékos ül le az asztalhoz: a gravitációs kölcsönhatás. Ennek ereje már eléri az erős kölcsönhatás szintjét, de „jobb lapokkal” rendelkezik, mert a kölcsönhatás nincs korlátozva az objektum méretével, ezért képes bármennyi neutron összetartására. De ne felejtkezzünk el a gyenge kölcsönhatásról, amelyik a neutron állományt fokozatosan protonná alakíthatja át, és ha túl sok a proton, az elektrosztatikus taszítás megakadályozhatja a neutroncsillag gyarapodását. Ez magyarázhatja, hogy a tömegük nem haladja meg a Nap háromszorosát.

Szupernóva robbanás

 A neutroncsillagok felfedezése 1935-ben James Chadwick (angol csillagász, 1891-1974, Nobel díj: 1935) nevéhez fűződik, aki a szupernóvák robbanását vizsgálta. A robbanás feltételét Subrahmanyan Chandrasekhar (1910-1995, Nobel díj: 1983) indiai csillagász adta meg, mely szerint ehhez akkora csillag kell, melynek tömege legalább nyolcszorosa a Napnak.  Amíg a csillagban elegendő a hélium termelő üzemanyag a fúzióhoz, addig a sugárnyomás megóvja a csillagot az összeroppanástól, de amikor ez kezd kifogyni a csillag összeroskad és hatalmas energia kibocsátás után csak egy viszonylag kis mag marad vissza, ami lehet egy fehér-törpe, vagy egy neutroncsillag. Ez a robbanás nem szállítja el az óriáscsillag eredeti forgásához tartozó impulzusnyomatékot, viszont a tömeg és még inkább a sugár sok nagyságrenddel lecsökken, amiért a forgást akadályozó tehetetlenségi nyomaték sok nagyságrenddel kisebb lesz, felgyorsítva a forgási frekvenciát akár 10 nagyságrenddel is. A neutronok rendelkeznek mágneses momentummal is, mert az alkotó kvarkok töltés súlypontja nem esik egybe. Így a másodpercenként akár több százszor megperdülő csillag mágneses mezője szétküldi az energiát a lágy rádiósugaraktól kezdve a kemény gamma-sugarakig, létrehozva a pulzárokat.

Mi lehet a fekete lyukak anyaga?

A fekete lyukakról csak keveset tudhatunk, mert egyedül azáltal vehetjük észre jelenlétüket, hogy eltakarják a mögöttük lévő csillagokat. Tömegükre is tehetünk becsléseket a csillagok mozgását tanulmányozva, amit befolyásol a fekete lyuk tömege is. Ezek jellemző tömege a neutroncsillagoknál hozzávetőleg egy nagyságrenddel nagyobb, de a galaxisok centrumában létező óriási fekete lyukak ezt a méretet is sokszorosan meghaladják. A Napnál tízszer nagyobb tömegű objektumokban a kötött fotonok pályasugara már 25 kilométer fölé nő, elérve a fekete lyukak kiterjedését, ha ezek sűrűsége a neutroncsillagokéval egyezik meg. Nem kell tehát a fekete lyukak sűrűségének meghaladni a neutroncsillagét ahhoz, hogy képesek legyenek visszatartani saját sugárzásukat. Kérdés azonban, hogy miért lehet tömegük jóval nagyobb, mint a neutroncsillagoké? Ez úgy képzelhető el, hogy itt nemcsak a neutronok, hanem a protonok, sőt az elektronok is csapdázódnak. A hatalmas gravitációs erő az elektronokat olyan pályára kényszerítheti, ahol a protonok belsejében nagy az elektronsűrűség. Nagy tömegű radioaktív atomokban ismert a K-befogás jelensége. Ez azt jelenti, hogy a legbelső pálya elektronja befogódik, és egy proton neutronná alakul át. Ez a folyamat épp fordítottja a béta-bomlásnak. A fekete lyukban a protonok belsejében lévő nagy elektronsűrűség miatt a K-befogás valószínűsége is megnövekszik, kompenzálva a béta-bomlást, és elősegítve, hogy a fekete lyukak tömege jóval nagyobb lehessen a neutroncsillagoknál.

Mekkora lehet a fekete lyukak sűrűsége?

Lehet-e a fekete lyuk tömegsűrűsége nagyobb, mint a neutroncsillagoké? A válasz nem az erős gravitáció koncepciója szerint, mert ennek F_sgr = ℏc/r² erősségét a tér maximális görbülete határozza meg, ami akkor jön létre, ha a fénysebességű forgások olyan geometriájú részecskéket hoznak létre, ahol a felület nullára zsugorodik a Lorentz kontrakció miatt. Ennél nagyobb torzulás már nem képzelhető el, ezért a sűrűség sem haladhatja meg a nukleonokét. De ne legyünk telhetetlenek, hiszen elegendő lenne a parányi kávéskanalat megtölteni evvel az anyaggal, hogy a Gizai piramis tömegének ezerszereséhez jussunk!

A blog további írásaira a "Paradigmaváltás a fizikában” című bejegyzés hívja fel a figyelmet a megfelelő linkek megadásával.