„A kvantummechanikán innen és túl. A fénysebességű forgás koncepciója” című könyvemben (Scolar kiadó, 2017) a modern fizika, mindenekelőtt a kvantummechanika elméletének bemutatására törekedtem, kiegészítve a fénysebességű forgások koncepciójával. Célom az volt, hogy a részecskefizika néhány rejtélyére magyarázatot találjak a tér fogalmának kiterjesztésével, amely nem csupán passzív tartály, amelyben a részecskevilág elhelyezkedik és végzi mozgásait, hanem megalkotja a részecskéket és meghatározza azok tulajdonságait: a tömeget, a töltést és a spint. Ennek megvalósítói a tér lokális tartományaiban fellépő eltérő szimmetriájú forgások, melyek véges kiterjedését a fénysebesség jelöli ki. Az elgondolás utat nyit a modern fizika néhány paradoxonjának feloldására, és közelebb vihet a fizika négy alapvető kölcsönhatásának – a gravitációs, elektromágneses, a gyenge és az erős kölcsönhatásának – egységes elmélete felé. A kiindulópont a relativitáselmélet által feltárt szingularitás, amely a látszólag semmiből anyagot teremt a fénysebesség által.

Vegyük sorra a részecskefizika különböző területeit, hogy lássuk a fénysebességű forgások szerepét az egyes fizikai jelenségek magyarázatában.

1.     A gravitáció és elektromágnesesség hasonlósága és eltérő sajátságai a fénysebességű forgások tükrében

Ez a fejezet jelentős mértékben támaszkodik „A pontszerű elektron legendájától a fénysebességű forgásokig” című bejegyzésre.

1.1 Az elektron pontszerűsége mellett szóló érvek

Pontszerű-e az elektron? Bizonyos kísérletek szerint igen! Erre adnak példát a Bhabha kísérletek. Bombázzunk elektronokat pozitronokkal! A találkozáskor a két részecske gamma sugárzás kíséretében annihilál. Könnyebb egy térben kiterjedt töltésrendszert eltalálni, ha annak nagy a mérete. A nagy energiájú szóráskísérletek azonban azt mutatják, hogy nagyon kicsi a találati valószínűség, és a mérési pontosság határain belül nulla az elektron töltéseloszlásának sugara. Más részecskéknél ez nem így van, így derítették fel különböző szórásvizsgálatokban a proton és neutron töltésének véges térbeli eloszlását.

Más jelenségekkel is összhangban van a pontszerűségi elv: az elektront ugyanis nem lehet kisebb egységekre felbontani. A felbonthatatlanság természetesen biztosan teljesül, ha tényleg pontszerű egy részecske, de ez önmagában még nem bizonyíték a pontszerűség mellett, mert a felbonthatatlanságnak más oka is lehet.

1.2.         Ellenérvek a pontszerűséggel szemben

Más oldalról, milyen érvek hozhatók fel a pontszerűség ellen? Mindenekelőtt feltehető a kérdés, hogy lehet-e bármilyen fizikai objektum végtelenül kicsi, felbontható-e az anyag végtelenül apró darabokra? Itt lép be a démokritoszi atomelv, amelynek álláspontja szerint, kell lenni valahol egy oszthatósági határnak, még ha mai tudásunk szerint ez a határ nem is az, amit ma atomnak nevezünk, sőt az atommag is felbontható nukleonokra (proton és neutron), de még ez sem a végső felbontási határ, hanem annak is vannak kisebb elemei: a kvarkok. Ismereteinket összegző Standard Modell szerint, a már tovább nem bontható elemi objektumok az említett kvarkok, de ide tartoznak még a fermionok közül az elektron és neutrínó család tagjai, valamint a különböző kölcsönhatásokat közvetítő bozonok, jelesül a fotonok, a W és Z részecskék, és a gluonok. A kérdés persze fennmarad, biztosak lehetünk-e abban, hogy amit ma a fizikai világ legapróbb építőköveinek tartunk, nem oszthatók-e mégis tovább, lehet, hogy ezek is valamilyen folytonos anyagból épülnek fel? Ha persze az elektron tényleg pontszerű, lezárhatjuk a kérdést, hiszen a pont az a végső matematikai határ, amely megfogalmazza a felbonthatatlan kiterjedés nélküliséget.

Ami azonban leginkább szembemegy a pontszerű elektron felfogásával, hogy az elektron olyan fizikai tulajdonságokkal rendelkezik, amely csak térben kiterjedt testeknek lehet: ezek a nyomatékot (momentumot) kifejező fizikai mennyiségek, jelesül az impulzus- és a mágneses nyomaték. Az előbbi arra utal, mintha az elektron tömege véges tértartományt foglalna el, az utóbbi szerint ez vonatkozik az elektron töltésére is.

1.3.         Az ellentmondás feloldása fénysebességű forgásokkal

Lehet-e egyáltalán olyan fizikai objektum, amely két ilyen egymásnak ellentmondó tulajdonsággal rendelkezik? Ha a részecskékhez fénysebességű forgásokat rendelünk, akkor igen! Ennek magyarázatát a relativitáselmélet Lorentz transzformációja adja meg. Ha hozzánk képest egy test valamilyen sebességgel mozog, annak méretét a mozgás irányában kisebbnek látjuk, és ha elérjük a fénysebességet, akkor a méret nullára zsugorodik. De ez csak a mozgás irányára igaz, mert a mozgásra merőlegesen a méret ugyanakkora marad. Képzeljünk el egy R sugarú köralakú objektumot, álló esetben a kerület hossza 2Rπ. Kisebbnek látja a külső szemlélő a kerület hosszát, ha forogni kezd a test ω = f/2π körfrekvenciával, és ha eléri a v = ωR kerületi sebesség a c fénysebességet, akkor a kör kerülete már nullára zsugorodik. De mi lesz a sugárral? Mivel a sugár mindig merőleges a mozgásirányra, ez változatlanul ugyanakkora marad. De lépjünk tovább és képzeljünk el egy olyan forgást, amelyik egyszerre két egymásra merőleges tengely körül megy végbe, ez már egy gömb felületét futja be. Ugyanis az első forgás által létrehozott kört, annak átmérője körül forgatva már kialakul a gömb. Kívülről nézve a gömb felülete már nullának látszik, ha a kerületi sebesség c, de sugarát továbbra is „láthatjuk”, ami alatt azt kell érteni, hogy amikor mérjük a gömbhöz tartozó nyomatékokat, annak nagysága arányos lesz a gömb sugarával, viszont hiába bombázzuk a gömböt kívülről, nem fogjuk annak felületét eltalálni. Persze, ha be tudnánk bújni a gömb belsejébe és avval együtt forognánk, a gömböt továbbra is szabályos gömbnek látnánk. Fénysebességgel mozgó rendszerekbe azonban nem tudunk belépni, ezért a fizikai törvényeket a külső megfigyelő szempontjából kell megfogalmazni.

1.     4.   Folytonosság, pontszerűség és diszkrét energiák

Hogyan kapcsolódik a részecskék pontszerűségének cáfolata a fizikai világ folytonosságának kérdéséhez? Az energia estén látszólag megszűnik a folytonosság, hiszen az atomban kötött elektronok diszkrét energiájúak, és adott frekvenciájú fény energiája is E = h·f nagyságú lépcsőkben változik. Fölvethető emiatt, vajon a tér és az idő se lenne folytonos? Nézzük először a klasszikus fizikát! Minden területen a folytonosságból indul ki, és differenciálegyenletekkel írja le törvényeit, akár mechanikáról, elektromágnesességről, vagy termodinamikáról van szó. Ez a szemléletmód abból indul ki, hogy – legalább is elvben – a mozgásokról folytonosan érkezik az információ a folytonosan érkező fény miatt. Gyakorlati szempontból ez a matematikai technika rendkívül hasznos, mert a végtelenül kis változások birodalmában lineárissá válnak a legbonyolultabb összefüggések is, ami nagyon megkönnyíti a számításokat. A bonyodalom az integrálásoknál következik be, amikor makroszkopikus méretekre terjesztjük ki a vizsgálatokat.

Jelenlegi kvantumfelfogásunk szerint sem beszélhetünk kvantált térről, vagy időről. Ennek oka, hogy a kvantummechanika operátorait az idő és a térkoordináták szerint differenciálhányadosok adják meg, már pedig ez megköveteli, hogy a koordinátákat végtelenül kis elemekre tudjuk felbontani, és folytonosnak kell lenni az állapotfüggvénynek is. De mégis hol az a pont, ami kvantumok kialakulásához vezet? Ez a körmozgás, amelyben a szögkoordináta 360 fokonként visszatér önmagába, ez az önmagába való visszatérés vetítődik ki az anyag hullámtermészetében is. Klasszikusan a mozgás pontról pontra követhető, mert elvben tetszésszerinti kis távolságban és időközben érkeznek hozzánk a fotonok, de ez már nincs így a kvantumok világában, mert a stacionárius állapotban „néma” az elektron, nem bocsát ki, vagy nyel el fotont, kizárólag csak a különböző állapotok közötti ugrásokat látjuk. Ha ebből visszakövetkeztetünk az elektronpályákra, az csak az egész pályáról, azaz a teljes körforgásokról adhat információt. Ez az információ a pálya impulzusnyomatéka, amit a redukált Planck-állandó egész számú többszöröse ad meg. Miért kötelező, hogy ez így legyen, miért nem keringhet tetszésszinti pályán az elektron? Ennek oka, hogy az elektron kötött pályára jutását a fotonok segítik elő. A szabadon mozgó elektronnak nincs pálya-impulzusnyomatéka, amikor azonban az atommag közelébe kerül, a vonzás gyorsítást, ez pedig foton kibocsátást okoz, de minden ilyen kibocsátás alkalmából ћ egységnyi impulzusnyomaték változás következik be. Végül, amikor kialakul a kötött stacionárius állapot, egész számú lépés határozza meg, hogy milyen impulzusnyomaték tartozik a landolási pályához.

De hol lép be a kvantummechanikai formalizmusba, hogy az állapotfüggvény által meghatározott impulzusnyomaték csak ћ egész számú többszöröse lehet? Ezt az garantálja, hogy az energia, impulzus és impulzusnyomaték operátoraiban ott szerepel a ћ konstans, mint a differenciálhányadosok együtthatója. Az impulzusnyomaték J_z = iћδ/δφ komponense a tengely körüli forgás poláris szögével képzett differenciálhányados, viszont a szög 360 fokos elfordulás a kezdő állapotnak felel meg. Ennek matematikai következménye, hogy az operátor sajátfüggvénye periodikus lesz, és a teljes fordulat során bekövetkező ismétlődések száma adja meg a diszkrét kvantumszámokat.

1.     5.  A tömeg és az impulzusnyomaték eredete

A tömeggel azonban bajban vagyunk, ugyanis véges tömeg nem mozoghat fénysebességgel, mert a c sebesség miatt végtelenül nagy tömeget észlelne a külső megfigyelő a relativitáselmélet szabályai szerint. Fordítsuk ezért meg a gondolatmenetet, és tegyük fel, hogy épp a c sebességű mozgás felelős a tömeg létrehozásáért! Ez a forgó test legyen az üres tér lokális tartománya, amelynek ugyan nincs tömege, de ez a nulla tömeg matematikai határértékként viselkedik. Az m tömeget, ha megszorozzuk annak reciprokával, akkor egyet kapunk: m·(1/m) = 1. Legyen hát az m tömeg végtelenül kicsi, ha ezt a Lorentz szabálynak megfelelő végtelenül nagy tényezővel szorozzuk, már véges értéket kaphatunk. Ily módon a relativitáselmélet tömegnövekedési szabályát kiterjeszthetjük a tömeg létrehozásának szabályává. A fénysebességű forgás tehát „teremtő” forgás, de az általa létrehozott tömeget már semekkora erő sem tudja úgy felgyorsítani, hogy az elérje a fénysebességet.  Ez a gondolatmenet a fénysebességű forgás koncepciója, amely feloldja az ellentmondást a szóráskísérletekben pontszerűként viselkedő elektron és a véges impulzusnyomaték létezése között. Ez a koncepció új funkciót ad a térnek, amely többé nem passzív tartály, amelyben a részecskék világa elhelyezkedik, hanem a részecskék megalkotója is. A térben minden mozgás sebessége relatív, de van egy nagy kivétel: a fénysebesség, amely a relativitáselmélet szerint mindig azonos vákuumban. Akár hozzánk közelítő, vagy távolodó objektum bocsátja ki a fényt, mindig azonos sebességgel teszi meg felénk az utat. Ezért a fénysebességet mint a tér szerkezeti állandóját foghatjuk fel.

Itt álljunk meg egy pillanatra és gondoljuk végig, hogy mi rejlik három fizikai fogalom: a tömeg, az energia és az impulzus mögött! Hétköznapi tapasztalatainkban az anyagot ösztönösen összekapcsoljuk a tömeg fogalmával, a fizikában azonban az energia és az impulzus játszik főszerepet, különösen a kvantummechanikában. Itt már úgy vetődik fel a kérdést, hogy mi az, ami állandó a változások mögött. Az időbeli állandóságot az energia fejezi ki, de ha a mozgó testre nem hat külső erő, akkor az impulzus jellemzi az állandó sebességű mozgást a térben. Körmozgások esetén, ha nincs külső forgatónyomaték, akkor az impulzusnyomaték képviseli az állandóságot a mozgásban. Ez azt jelenti, hogy az energia, impulzus és impulzusnyomaték a primer fizikai mennyiség, és a tömeg ehhez képest csak másodlagos „segéd paraméter”. Az E = mc² összefüggést úgy kell értelmezni, hogy az energiának van „tömege”, és nem a tömegnek van energiája. Erre a legtisztább példa a foton, amelynek egyaránt van energiája, impulzusa és impulzusnyomatéka, de nem tartozik hozzá nyugalmi tömeg.

 Ha a térben valamilyen ω körfrekvenciával forgás alakul ki, az véges méretű körpályát fog kijelölni, és ennek sugarát az R = c/ω szabály adja meg. Fogjuk úgy fel a fotont, mint a tér forgását, rendeljük hozzá az ω körfrekvenciához az E = ћω energiát. A foton azonban természeténél fogva c sebességgel száguld, vagyis a fénysebességű mozgás által kialakított körpálya egyúttal a forgási tengely irányában is halad szintén fénysebességgel. A foton mozgását úgy is elképzelhetjük, mint a henger palástja mentén feltekeredő csavart. Tisztában kell lenni vele azonban, hogy ez csak szemléltetés, hiszen a fotont alkotó térmozgást nem láthatjuk. Helyesebb ezért a foton és a további elemi részecskék esetén a tér olyan kettős mozgásairól beszélni, amelyet a szimmetriaviszonyok határoznak meg. Körmozgásokban a centrifugális erőn kívül Coriolis erő is fellép, ha ott jelen van egy második mozgás is. Ennek viszont nincs szerepe a fotonoknál, mert ott a haladási irány párhuzamos a forgás tengelyével. A foton másik fontos tulajdonsága, hogy térben nyitott a struktúrája: egy végén nyitott hengerpalást.

Bár a foton nem lehet nyugalomban és így nyugalmi tömege sincs, rendeljük hozzá a tömeg-energia ekvivalencia alapján az m = E/c² fiktív tömeget, ez segíteni fog, hogy kapcsolatot találjunk az energia és az impulzusnyomaték között. Ennek a tömegnek szorzata a fénysebességgel már mérhető mennyiséghez: az m·c impulzushoz vezet, amit ha megszorzunk az R sugárral is, megkapjuk a foton impulzusnyomatékát: ћ = h/2π. A számítás eredménye tehát épp akkora impulzusnyomaték, mint amekkorát Planck annak idején a foton számára megállapított, vagyis a fiktív tömeg fogalmának bevezetése hasznosnak bizonyult! Még arra is választ kapunk, hogy bár a foton frekvenciája és energiája rendkívül széles határok között változik, az impulzusnyomaték mégis pontosan ugyanakkora marad, hiszen amíg a fiktív tömeg a frekvenciával arányos, addig a sugár fordítva arányos vele, a c sebesség pedig állandó.

De térjünk rá a kettős forgással értelmezett elektronra, amely viszont térben zárt struktúra, mégpedig egy gömb. Itt a gömb felülete zsugorodik nullára a fénysebességű forgás miatt, ez tükröződik a Bhabha kísérletben is, amely szerint az elektron hatáskeresztmetszete a szórás kísérletekben nulla. A kettős forgást úgy foghatjuk fel, hogy először egy kiválasztott tengely körül 2π szögű forgatást végzünk el, majd ezt egy erre merőleges tengely körül megismételjük, azaz összességben 4π szögű forgatást hajtunk végre. Ennek a gömbforgásnak frekvenciája az egytengelyű forgáshoz képest fele akkora lesz, azaz Ω = ω/2, a kétszer olyan hosszú szögtartomány miatt. Ezt a gömbfrekvenciát hozzuk kapcsolatba a részecske tömegével: E = mc² = ћΩ, vagyis Planck eredeti gondolatát – aki feltárta ezt az összefüggést fotonokra – kiterjesztjük a részecskékre is. Itt a zárt tértartomány miatt már valódi tömegről beszélhetünk. Ez a felfogás megfelel a kvantumelektrodinamika (QED) szellemének is, ahol az alkalmazott formalizmusban az elektronokat és fotonokat egyaránt oszcillátorok – azaz rezgő objektumok – képviselik. Az impulzusnyomaték egyik komponensét úgy kapjuk meg, ha az egyik tengelyforgás w körfrekvenciáját vesszük alapul, amelyik a fotonhoz viszonyítva kétszeres, azaz ω = 2mc²/ ћ. Ezt behelyettesítve az impulzusnyomaték kifejezésébe, kapjuk, hogy m·c·R = ћ/2. Így jutunk el az S = ½ spinhez, amelyik minden elemi fermion sajátja bármekkora is legyen a tömeg. (Spinnek nevezzük a ћ egységben megadott impulzusnyomaték együtthatóját, ez fotonoknál S = 1, az elektronnál S = ½ értéket vesz fel. Más részecskéket is a spinjükkel jellemezzük, amely bozonoknál S = 1 és fermionoknál S = ½. Az összetett szerkezetű részecskéket is ez alapján osztályozzuk: a spin mindig egész számú bozonoknál, és „félegész” fermionoknál.)

Kvantummechanikában az elektronspin S_z komponenséhez az +½ és -½ sajátértékeket lehet hozzárendelni, és ennek sajátfüggvénye e^±½iφ. Ez a függvény teljes körülforgáskor, azaz φ = 2π értéknél, –1 lesz, és csak a 4π dupla forgásnál lesz +1. Az S = ½ spinekből felépülő rendszerekben a szimmetriákat összegző csoportelmélet ezért a 2π szögű forgást nem tekinti identitásműveletnek, és evvel a szimmetriaművelettel kibővítve bevezeti a kettős csoportokat. Ennek az ad hoc műveletnek a kettős forgás koncepciója adja meg a magyarázatát. A kettős csoport voltaképp a kettős forgásokra épülő matematikai reprezentáció.

1. 6. Centrifugális erő és az erős gravitáció

Ha egy m tömegű test ω körfrekvenciával kering az R sugarú körön, akkor arra F_C = mω²R = mv²/R centrifugális erő hat. Emiatt felvetődik a kérdés, hogy milyen erő képes stabilizálni a forgást a szétrepítő erő kiegyenlítésével? Helyettesítsük be a centrifugális erő képletébe az előzőekben alkalmazott összefüggéseket, ekkor a fénysebességű forgás centrifugális ereje F_C = ћc/R² lesz. Az ellensúlyozó erő megtalálásához forduljunk az általános relativitáselmélethez, amely a tér görbületével magyarázza a gravitációs erőt.

A Newton törvény szerint az M tömegtől r távolságban lévő m tömegre ható gravitációs erő F_G = GmM/r², illetve a hozzá tartozó potenciális energia V_G = GmM/r, ahol G az általános gravitációs állandó. A gravitációs erő tart egyensúlyt az mv²/r centrifugális erővel, amiért

v² = GM/r = V_G/m

Az összefüggés mutatja, hogy a forgás kerületi sebessége nem függ a keringő test tömegétől. Mivel a teret határértékben nulla tömegűnek tekintjük, maga a tér is forog az M tömeg körül, de ennek sebessége messze elmarad c-től. A kerület bizonyos mértékű csökkenése azonban így is bekövetkezik a Lorentz kontrakció miatt, amelyet 2π-vel osztva definiáljuk az r_G < r görbületi sugarat. Ennek segítségével adhatjuk meg a tér görbületét:

. Görbület = 1 – (r_G/r)² = v²/c²

Ez a görbület kis értéket vesz fel a részecskét körülvevő térben, viszont egységnyi lesz fénysebességű forgások esetén. A fenti két összefüggés kapcsolatot teremt a görbület és a gravitációs potenciális energia között:

V_G = Görbület·mc²

A speciális és általános relativitáselmélet összekapcsolásából tehát az adódott ki, hogy a fénysebességű forgás által előidézett egységnyi térgörbület miatt mc² nagyságú potenciális energia jön létre. Eredetileg a görbületet a M tömeg hozta létre, amely vonzza a tőle r távolságban lévő „külső” m tömeget, de amikor a részecske saját tartományába érünk az R sugárnál, ott már nem „külső” tömegről van szó, hanem a fénysebesség által létrehozott saját tömegről, azaz m átveszi M szerepét. Ez a felfogás viszont új értelmet ad a részecskék nyugalmi energiájának, amely nem más, mint a tér torzulásának potenciális energiája fénysebességű forgások esetén. Úgy is fogalmazhatunk, hogy a tér görbülete biztosítja azt az erőt, amely a fénysebességű forgást stabilizálja. Ezt az erőt, amely az R sugarú részecskénél ћc/R² nagyságú lesz, nevezhetjük erős gravitációnak.

A részecskeképződés tehát nem kíván külső energiát, csak az impulzusnyomaték forrását kell biztosítani. Evvel magyarázatot kapunk arra is, hogy a béta-bomlás folyamatában, amikor a neutron protonná alakul át egy elektron és egy neutrínó kibocsátásával, hogyan képződhet olyan közvetítő bozon (W bozon), amelynek tömege közel százszor haladja meg a kibocsátó neutronét.

1. 7. Az elektromos töltés eredete

De honnan származik az elektronok és más részecskék töltése, vagyis hogyan jön létre az elektromágneses kölcsönhatás, és miért van sok nagyságrenddel eltérő tömegű részecskéknek azonos töltése, és miért lehet a töltés előjele kétféle: pozitív és negatív? A QED elmélet részben válaszol a kérdésekre, amikor feltételezi, hogy virtuális fotonok áradnak ki a töltésekből, illetve nyelődnek el. Ezek közvetítik az erőhatást a töltések között, ami lehet vonzás, vagy taszítás, a töltések relatív előjelétől függően. A fotonoknak ugyanis más a polaritása attól függően, hogy a kibocsátó töltés előjele pozitív, vagy negatív, és a fotonok szuperpozíciója dönti el, hogy mikor jön létre taszítás, illetve vonzás a töltött objektumok között. Ha ellentétes a két foton polaritása, akkor a két töltés közötti tartományban az amplitúdók kioltják egymást, ez okozza a vonzást. Ellenkező esetben az amplitúdók összeadódnak ebben a tartományban, és taszítás lesz az eredmény. A QED elmélet azonban nem lép tovább, mert nem válaszol a kérdésre: miért lépnek ki virtuális fotonok a töltésekből? A fénysebességű forgás koncepciója erre a kérdésre is keresi a választ. Ennek magyarázatát egyrészt a tér szerkezetére, másrészt tehetetlenségi erőkre lehet visszavezetni.

A háromdimenziós teret kétféle módon építhetjük fel. Ha megadunk két merőleges koordinátát, nevezzük x-nek és y-nak, akkor a harmadik tengely két irányban is felvehető: z mutathat felfelé, vagy lefelé. A két geometria nem forgatható egymásba, ahogy a jobb és bal kezünk se, viszont ezek egymás tükörképei. Ezt a kettősséget nevezzük kiralitásnak. Ez a kettősség jelenik meg a kettős forgás esetén is. Válasszuk ki az első forgást az óramutató járásával egyezően, a másik erre merőleges forgás iránya viszont lehet akár egyező, akár ellentétes az óramutató járásával, azaz a kettős forgás is lehet kétféle kiralitású. Ennek megfelelően létezhet kétféle részecske, kétféle anyag. Ez áll az anyag és antianyag kettőssége mögött. Mi történik, amikor az anyag találkozik az antianyaggal, például az elektron a pozitronnal? Ilyenkor a két részecske megsemmisül, és két gamma foton távozik. Ezt képszerűen értelmezi a kettős forgás modellje: két ellentétes irányú forgás megsemmisíti egymást, de a második forgás megmarad, ez pedig nem más, mint a két gamma foton!

Ez arra is rámutat, hogy miért sikertelenek azok a matematikai próbálkozások, amikor a részecskefizikában – ilyenek a húrelméletek is – négy, öt vagy még további térdimenziókkal próbálkoznak. Ha például létezne egy negyedik térdimenzió, akkor a térnek nem két, hanem négyféle kiralitása lenne, tehát nemcsak anyag és antianyag létezne, hanem volna még két további anyagtípus is. Ennek hiánya viszont arra mutat, hogy meg kell elégednünk a jól bevált háromdimenziós világképpel. De mi a helyzet Minkowski négydimenziós téridő koncepciójával? Van egy alapvető különbség a tér és az idő dimenziók között. Amíg a térdimenziók kétirányúak: föl-le, jobbra-balra, előre-hátra, az időben nem lehet visszafelé menni a múltba. Emiatt a téridő nem jár további anyagtípusok megjelenésével.

De milyen erő készteti a fotonokat, hogy kilépjenek a töltött részecskékből? Ha forgó rendszereken belül van egy további mozgás, arra hat egy újabb tehetetlenségi erő, amit Coriolis erőnek nevezünk. Ennek iránya egyaránt merőleges a másodlagos mozgás irányára és a forgás tengelyére, amit vektorszorzat fejez ki:

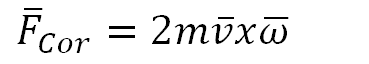
A második forgás iránya az első forgás tengelyéhez képest körbefut, ami szinuszos függést eredményez, melynek amplitúdója c sebesség mellett ħc/R²:

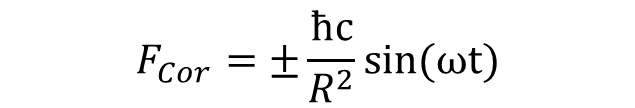
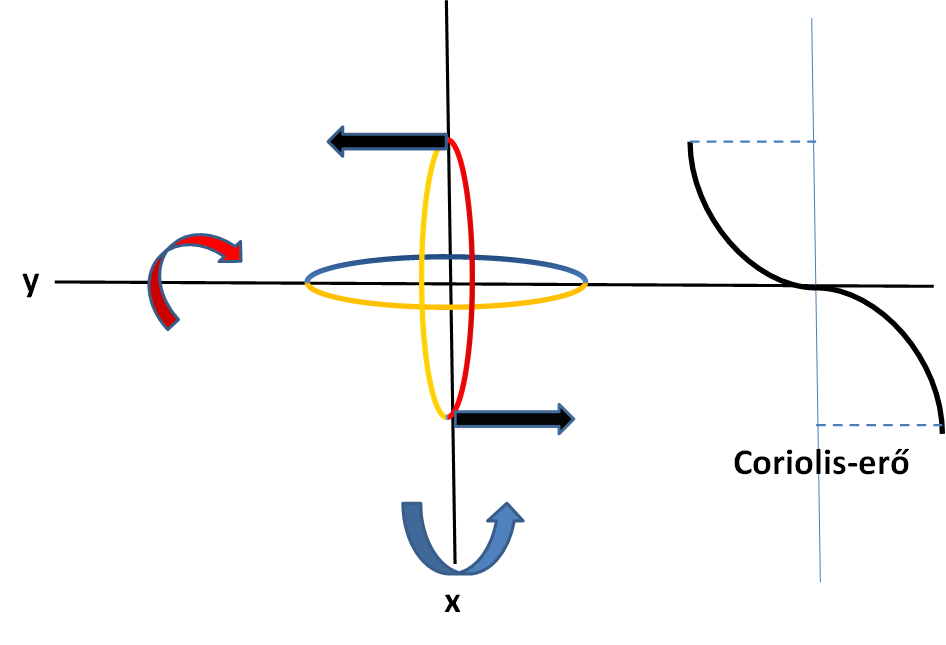
1. Ábra. A Coriolis erő szemléltetése kettős forgások esetén. Az x-tengely körül megy végbe az elsődleges, az y- körül a másodlagos forgás, amire ható erő két maximumát a fekete nyilak mutatják, a jobboldalon pedig a szinuszos változás látható

Ez az erő párhuzamos a második forgás tengelyével, és előjelét a kettős forgás kiralitása határozza meg. A Coriolis erő átlaga nulla, amely viszont ω frekvenciával változó erőt generál a kettős forgás gömbjének felszínén, amelynek nagysága a centrifugális erővel együtt nulla és 2ħc/R² között ingadozik. A részecske sajátforgását stabilizáló erős gravitáció görbületi sugara is ennek ütemében pulzál, amely forrásává válik a külső térbe távozó egytengelyű forgásoknak, amit a QED virtuális fotonoknak nevez.  A kiralitásnak megfelelő előjel a forgás polaritását határozza meg. A kilépési hatásfokot az α = 1/137 Sommerfeld állandó adja meg, amely meghatározza a Coulomb kölcsönhatásban definiált elemi töltés nagyságát: e² =αħc. A töltés tehát nem függ a részecske méretétől! Evvel választ kapunk arra a kérdésre is, hogy a rendkívül eltérő tömegű részecskéknek miért ugyanakkora az elektromos töltése.

De térjünk még vissza az einsteini gravitáció létrejöttének okára is. Ezt az M tömeg körüli térforgásokra és az általa kiváltott térgörbületre vezettük vissza. Két kérdés azonban tisztázatlan maradt. Eddig csak a frekvenciáról beszéltünk, de egyrészt milyen irányban történik a forgás, másrészt miért fog forogni a tér?

Az első kérdés megválaszolásához a kvantummechanika szemléletmódját vehetjük alapul. Amikor atomok és molekulák elektronjainak pályájáról beszélünk, csak valószínűségi kijelentéseket tehetünk az állapotfüggvény segítségével. Ennek oka, hogy nem tudjuk az elektron pályáját stacionárius állapotban nyomon követni, csak az ugrásokat láthatunk két pálya között. Természetesen a tér forgásait sem láthatjuk, ezért konkrét forgási pálya helyett csak annyit mondhatunk, hogy a centrumtól mért valamilyen r távolságban minden pályairányhoz azonos valószínűség tartozik. Amikor egy égitest pályáját nyomon követjük, az már egyet kiválaszt a lehetséges pályák közül. Ennek felel meg a kvantummechanikában, amikor az állapotfüggvény által megengedett lehetőségek közül a mérés egy konkrét értéket ad meg. A kvantummechanikából ezért nem a kvantumot kell átvenni, hanem az elmélet valószínűségi felfogását.

A másik kérdés megválaszolásához segítséget ad az a kép, amivel az elektromágneses kölcsönhatást közvetítő virtuális fotonok kilépését magyaráztuk. De mielőtt ezt bemutatnánk, tegyünk egy újabb kitérőt az elektron anomális mágneses nyomatékának kérdésköréhez.

1.     8. Az elektron anomális mágneses nyomatéka

Az elektronok véges mágneses nyomatékkal rendelkeznek, melyet a relativisztikus Dirac-egyenletből lehet származtatni:

    M_S = 2μ_BS,

ahol μ_B = eћ/2mc a Bohr magneton. Ezt származtatni tudjuk az e elemi töltés fénysebességű forgásából is! Itt hangsúlyozni kell, hogy ebben a mozgásban az elektron saját mágneses nyomatéka végez körforgást külső mágneses mezőben (Larmor precesszió), azaz a fénysebességű kettős forgásra rárakódik egy ahhoz képest lassú egytengelyű forgás is. Alkalmazzuk a mágneses nyomaték számításánál a klasszikus elektrodinamika M = IF/c törvényét! Itt az f frekvenciával forgó e töltés árama I = e·f = eω/2π, a bezárt kör területe F = R²π.  A behelyettesítések után kapjuk, hogy:

M_S = eR/2 = μ_B = 2μ_BS

Az atomban „keringő” elektronok pályamozgásához is tartozik mágneses nyomaték, mégpedig ha a pálya impulzusnyomatéka Lħ, ennek nagysága M_L = μ_BL. Összehasonlítva a két nyomatékot, feltűnik, hogy a spin szorzójaként szerepel egy 2-es együttható, de mi ennek az eredete? Ennek megválaszolásával a fizika már régóta küszködik, és látszólag a klasszikus fizika nem tudja megadni a választ. A kettős forgás koncepciója azonban kézenfekvő magyarázatot ad! A spint kettős forgásból származtatjuk, ezért lesz S = ½, viszont a mágneses nyomaték a mágneses mező körüli Larmor precesszióból – azaz egytengelyű forgásból – ered. Az egytengelyű forgásból származtatott mágneses nyomatékot a kéttengelyű forgásból kapott impulzusnyomatékkal összevetve lép fel a formulában a 2-es faktor.

A mágneses nyomaték rendkívül pontos kísérleti értéke azonban nem pontosan egyenlő a relativisztikus Dirac-egyenletből származtatott faktorral, hanem kissé nagyobb:

 M_S = 2,002319304362 μ_BS

Mi okozza ezt a kis növekményt? A kvantum-elektrodinamika (QED) mezőelmélete erre rendkívül pontos megoldást ad különböző szintű közelítések keretében. A QED alapgondolata, hogy az elektromos töltések vonzó-taszító hatását virtuális (közvetlenül nem detektálható) fotonok hozzák létre, amelyek állandóan kibocsátódnak és elnyelődnek, és így fluktuációt okoznak a részecske pozíciójában. Ez viszont megnöveli a mágneses nyomatékot az áram által körüljárt terület kiterjesztése által. A nehéz veretű időtől-függő perturbációs eljárás számba veszi a fotonok és elektronok legkülönbözőbb mozgásait, emissziós, abszorpciós, párképződési és annihilációs folyamatait, és ezáltal tíz jegy pontossággal tudja reprodukálni a kísérletileg mért értéket. Itt most bemutatjuk, hogy a legfontosabb korrekciós tagok a klasszikus elektrodinamika eszközeivel is származtathatók, ha a fénysebességű forgások elvére támaszkodunk.

A részecske belső tartományából való foton kibocsátást a kettős forgás által kiváltott és ћc/R² amplitúdójú Coriolis-erő oszcillációja okozza, és a fotonok kilépési hatásfokát az α = 1/137,036 Sommerfeld állandó adja meg. Az elektron saját mozgását stabilizáló erős kölcsönhatásnak a ћc/R² nagyságú centrifugális erő és a kiáramló αћc/R² nagyságú Coulomb erő összegét kell ellensúlyozni, ami lecsökkenti az erős gravitáció R_G sugarát a centrifugális erő R_C sugarához képest. Viszont ezt a hatást csak a mágneses mezőre merőleges síkban kell figyelembe venni a gömb egész felületén ható centrifugális erővel szemben, ezért a korrekciós tagban fellép a sugár/kerület 1/2π tényezője is: 

ћc/R_G² = ћc/R_C² + (α/2π)ћc/R_C²

Innen kapjuk a töltés által körüljárt felület megnövekedését:

R_C²/R_G² = 1+ α/2π

Ez az arány jelenik meg az elektron anomális mágneses nyomatékának első korrekciós tagjában. (Bár a mágneses nyomaték lineárisan függ a részecske sugarától, mégis a felülettel való arányosság határozza meg a korrekciót, mert a tömeget létrehozó ω = c/R körfrekvencia azonos marad.) A számítás tovább finomítható, ha figyelembe vesszük, hogy a kiáramló fotonok energiája csökkenti az elektron belső terének energiáját 1 - α/2π mértékében:

R_C²/R_G² = 1+ α/2π(1 - α/2π)

Ekkor a mágneses nyomaték már csak a hetedik tizedes jegyben tér el a kísérleti adattól: M_S = 2,00232010 μ_BS.

A QED számítások még három további tizedes jegyig rekonstruálják a kísérleti értéket, de ekkor már rendkívül összetett virtuális folyamatok sokasága is szerepet játszik, amit a Feynman diagramok foglalnak össze (R. P. Feynman: QED. The strange theory of light and matter, Princeton University Press, 1986). A klasszikus fizika eszközével számított érték is tovább közelíthető a kísérleti adathoz, ha figyelembe vesszük az elektron-pozitron párkeltést is. Ilyenkor nem a tömeg „megtermeléséről” van szó, hanem megfordul az elektromágneses energia áramlási iránya: eredetileg az elektronokból léptek ki a fotonok, ekkor viszont a fotonok építik fel az elektront és a pozitront. A belső energiának α/2π hányadát képviseli a virtuális foton mező a Larmor precesszió síkjában, a párkeltéshez egyfelől két foton kell, másfelől két részecske keletkezik, és ennek megvalósításához a kilépő energia α/8π hányadát kell „befektetni”. Ezt számításba véve a tovább finomított összefüggés:

R_C²/R_G² = 1+ α/2π(1 - 5α/8π)

Az innen számított mágneses nyomaték M_S = 2,00231944 μ_BS még közelebb került a kísérleti adathoz. További korrekciós tagok bevezetése nélkül is figyelemre méltó, hogy a fénysebességű forgások koncepciójára támaszkodva a klasszikus fizika egyszerű eszközei is meglepően jó egyezést adnak a kísérlettel, amihez ugyanakkor a QED rendkívül bonyolult és számítógép igényes integrálásokkal jut el.

A mágneses nyomaték anomáliájának okát szemléletesen avval magyarázhatjuk, hogy az elektronnak kettős héja van. A belső felület határozza meg a tömeget és az impulzusnyomatékot, a külső felület viszont a fluktuációs mozgás miatt alakul ki, amiben a belső gömb „lötyög”, és emiatt megnövekszik a felület, amit a töltés körbejár.  

1.     9. A fénysebességű kettős forgás gravitációs mezője

Folytassuk annak a kérdésnek a vizsgálatát, hogy miért forog a tér az M tömegű fizikai objektumok körül? Erre a rövid válasz, hogy ennek oka, a részecskét alkotó kettős forgás „kiáradása” és elnyelődése a külső térből! Ez annyiban hasonlít a virtuális fotonok szerepéhez, hogy a gravitációs mezőt is folytonos emisszió és abszorpció építi fel. Mivel a távolság négyzetével növekszik az elért felület, így a mezőerősség r² arányában csökken. A két erőtörvény ebben hasonlít egymásra. Másik hasonlóság a két kölcsönhatás között, hogy a mezőt létrehozó és a hatást átvevő objektumok – itt a töltés, ott pedig a tömeg – szimmetrikus, egyenrangú, szerepet töltenek be: gravitációnál két tömeg, a Coulomb kölcsönhatásban két töltés szorzata szerepel. A szorzat két tényezőjének azonos szerepe annak felel meg, hogy az emisszió és abszorpció két egyenértékű tükörfolyamat. Mégis van egy alapvető különbség a két kölcsönhatás között: amíg a foton fénysebességű forgás, amihez kvantált impulzusnyomaték tartozik, addig a lassú kettős forgások nem hoznak létre impulzusnyomatékot és így nincs kvantumuk sem. A különbség abban nyilvánul meg, hogy az elektromágneses kölcsönhatás nemcsak pályafenntartó mező, hanem pályaváltozásokat (ugrásokat) is indukál, ez előbbi közvetítőit nevezi a QED virtuális, az utóbbit valódi – megfigyelhető – fotonoknak. Az energia nyelvén megfogalmazva ez azt jelenti, hogy a fotonok egyrészt megalkotják a kölcsönhatás potenciális energiáját, másrészt van kinetikus energiájuk és ehhez kapcsolódóan impulzusuk is. A lassú gravitációs kettős forgások viszont kizárólag potenciális energiát hoznak létre a térgörbületek által, anélkül, hogy rendelkeznének kinetikus energiával, illetve olyan lökő erővel, amely a pályák között ugrásokat hozhatna létre. Ennek a döntő különbségnek figyelmen kívül hagyása okozhatja, hogy immár száz éve kudarcba fulladnak az erőfeszítések, hogy megtalálják a gravitáció kvantumát, és megalkossák a fizika négy kölcsönhatásának egységes mezőelméletét.

Az utolsó megválaszolandó kérdés, hogy milyen erő indítja útjára a kettős forgásokat a részecske határán kívülre? Ez az Euler erő, ami akkor lép fel, ha a forgási frekvencia megváltozik! Ez a forgás felgyorsításával, vagy lassításával szembeni tehetetlenség, amelynek nagyságát vektoriális szorzat fejezi ki:

A fénysebességű forgás koncepciója szerint a részecske ω frekvenciája gyakorlatilag nullára csökken, amikor átlépjük a részecske R sugarát, és mivel ott a gravitációs forgás frekvenciája nagyon kicsi, a frekvenciaváltozás egyenlő a forgási frekvenciával, azaz Δω = ω. A Δt idődifferencia megadásához az R sugarú elektron αR vastagságú héjának αR/c áthaladási idejét vehetjük alapul, amiért a forgómozgás irányában ható Euler erő:

Ez hatalmas erő, amely még a részecskét stabilizáló erős kölcsönhatást is 137-szer meghaladja, viszont ennek munkavégző képessége az αR szakaszra korlátozódik, azaz V_Euler = ħc/R = Mc². Bár a részecske forgási frekvenciája az R határon átlépve közel nullára csökken, mégis valamennyi megmarad, ezt úgy is felfoghatjuk, mint a nem kvantált folyamatok folytonossági követelményét. A kilépő forgási frekvencia miatt van tömegvonzás! A forgás kiléptetését okozó erőt származtathatjuk az Euler potenciálból. Ennek a potenciálnak viszont két független forgást kell kivinnie a részecske külső terébe, és emiatt a létrehozott V_G/m gravitációs potenciál az Euler potenciál négyzetével lesz arányos:

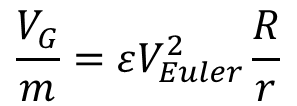
Az ε arányossági konstanst meghatározhatjuk, ha összevetjük a két potenciált a részecske r = R határánál, amiből kapjuk, hogy 

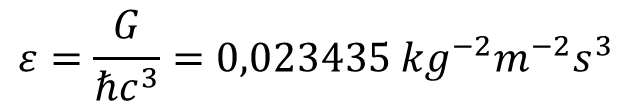
Az ε konstans a fizikában korábban még nem alkalmazott állandó, amely hasonló szerepet tölt be a gravitáció elméletében, mint az a Sommerfeld állandó az elektromágnességben. Ez az állandó úgy fogható fel, mint csillapítási tényező, amely meghatározza az Euler erő képességét gravitációs forgások létrehozására. Mivel a gravitációt két összekapcsolt forgás hozza létre, a vonzóerő nagyságát a tömeg határozza meg, szemben a töltések által meghatározott Coulomb erővel, amelyet egytengelyű forgások, azaz fotonok közvetítenek. A kettősforgás kiralitása viszont nem játszik szerepet a görbületi sugár előjelében, amely magyarázza, hogy a gravitáció kizárólag vonzást, és nem taszítást hoz létre a részecskék között. Arra már korábban utaltunk, hogy az elektromágnesesség vonzási-taszítási kettőssége a fotonok két lehetséges forgási irányával van összefüggésben.

Einstein általános gravitációs egyenletéből Schwartzshield határozta meg a módosított gravitációs potenciált körmozgások esetén, amely kiegészíti az eredeti Newton formulát:

V_G/m = GM/r + G²M²/c²r² 

Ez a kiáramló kettős forgások koncepciójával is magyarázható. Az M és m tömegek közötti GMm/r gravitációs potenciális energia fele-fele arányban hozzájárul a részecskék lokális Mc² illetve mc² energiájához, ami viszont megegyezik a helyi Euler potenciális energiával. Emiatt megnövekszik a kettős forgás kibocsátási hatásfoka is:

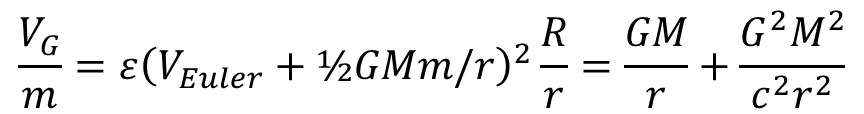
Itt a négyzetre emelésnél az utolsó kis tagot elhagyva reprodukáltuk a Schwartzshield potenciált. Ebből látható, hogy a kettős forgásokra alapozott gravitációs modell összhangban van az általános relativitáselmélet formalizmusával is.

1.     10.   Miért lesz végtelen az elektron sajátenergiája a QED elméletben?

A QED elmélete látványosan szép eredményre vezet az elektron anomális mágneses nyomatékának meghatározásával, mégis van egy súlyos hibája: a sajátenergia első perturbációjának számítása végtelenül nagy értékre vezet. Ha ezt önkényesen elhagyjuk, akkor a további tagok rendkívül nagy pontossággal adják vissza a kísérleti értéket. Az elméletnek ezt a gyenge pontját a klasszikus elektrodinamikától örökölte, amikor számba vette az elektron elektromos kölcsönhatásának sajátenergiáját. Ezt úgy végzik el, hogy az elemi töltést végtelenül kis elemekre bontják fel, és először elviszik ezeket a töltéseket végtelen távolságba, majd kiszámítják a munkavégzést, amikor a töltést egyetlen pontba egyesítik. Az alkalmazott módszer eleve ellentmondáson alapul, amikor felbontja az oszthatatlan elemi töltést. A végtelen sajátenergia pedig onnan származik, hogy az integrálást nulláig viszik, mintha tényleg egyetlen matematikai pontban lenne a töltés, ahol már a taszítási erő ellen végzett munka végtelenül nagy. A QED elmélete is a kölcsönhatást nulláig kiterjesztett integrálokkal írja fel, ezért jelenik meg ott is a szingularitás. Ezt a hibát kiküszöböli a fénysebességű forgás koncepciója, amely véges sugarat határoz meg a részecske számára. Az elektromágneses mező energiája a részecske által a belső tartományból a külső térbe kiküldött hányad, amit az a Sommerfeld-állandó ad meg, míg az mc² sajátenergia döntő hányada (1 – α = 0,9927-ed  része) belül marad. Helytelen ezért az olyan próbálkozás is, amely az elektromágneses mező energiájával akarja értelmezni az mc² nyugalmi energiát (erre alapozzák a klasszikus elektronsugarat).

1.     11.  Összetett részecskék spinje és a véges hatáskeresztmetszet

A pontszerűséggel kapcsolatban érdemes még kitérni arra a kérdésre is, hogy a proton töltéseloszlása a mérések szerint nem pontszerű, bár az elektronhoz hasonlóan a spinje ½. Az elektron impulzusnyomatékát a fénysebességű kettős forgásra vezettük vissza, ezért ha evvel magyaráznánk a proton spinjét is, akkor nulla hatáskeresztmetszetet várnánk proton esetén a szóráskísérletekben. Ha nem tudnánk az elméletből, hogy a proton három kvarkból épül fel, akkor már a véges hatáskeresztmetszet létezéséből levonhatnánk a tanulságot, hogy a proton összetett szerkezetű! Mivel a valóban elemi – tehát tovább nem osztható – fermionoknak a kettős forgás koncepciója szerint ½ a spinje, így a spinek összeadási szabályából már következik, hogy legalább három komponensből épül fel a proton, ugyanis két ½ spin összege nulla, vagy egy lehet. Egyébként az összetett részecskék családjában vannak két kvarkra bontható mezonok is, ahol tényleg a spin 0, vagy 1 értéket vesz fel. Három ½ spin alkothat akár ½, akár 3/2 spint is. Léteznek ennek megfelelően olyan barionok is, melyeknek spinje 3/2. (Barionnak nevezzük a három kvarkból, vagy antikvarkból felépülő részecskéket, ennek legstabilabb két tagja a proton és a neutron).

Következő rész:

 A blog további írásai: "Paradigmaváltás a fizikában"