2. Pillantás az elemi részecskék belsejébe: az erős-kölcsönhatás

Az első részben eljutottunk odáig, hogy alapvető kapcsolatot találtunk az elektromágnesesség és a gravitáció között: amíg az elektromágnesességet az egytengelyű fénysebességű forgások, azaz a fotonok közvetítik, addig a gravitációt spinnel nem rendelkező kettős forgások hozzák létre. A potenciálteret virtuális forgások építik fel a fermionokból kilépve és elnyelődve, de amíg a fotonok a fénysebességű forgások révén impulzusnyomatékkal és így kvantummal rendelkeznek, ez a tulajdonság hiányzik a kilépés után a távolsággal lassuló kettős forgásokból. A második részben tovább lépünk az erős kölcsönhatások birodalmába, és feltesszük a kérdést, vajon a fénysebességű forgások alkalmasak-e arra, hogy választ adjanak az erős kölcsönhatás által feltett kérdésekre, mindenekelőtt megtudjuk-e magyarázni, hogy miért rendelkeznek a kvarkok törttöltésekkel és mi a szín-kvantumszám eredete, amelyet az erős kölcsönhatás közvetítői, a gluonok alakítanak ki.

Ez a fejezet jelentős részben a „Pillantás az elemi részecskék belsejébe: kvarkok és gluonok különös világa” című korábbi íráson alapul.

2. 1. A Kvarkok mozgásformái és a húrrezgések

Közelebb juthatunk a kvarkok és gluonok különleges tulajdonságainak megértéséhez, ha valamilyen geometriai alakzathoz tudjuk kötni mozgásukat és szerkezetüket. A kvarkok fermion típusú elemi részecskék és spinjük S = ½. Evvel szemben a kölcsönhatásokat közvetítő elemi bozonok spinje S = 1, ami egyaránt vonatkozik az előzőekben tárgyalt elektromágneses kölcsönhatást közvetítő fotonokra, a következő részben ismertetésre kerülő gyenge kölcsönhatás W és Z bozonjaira, valamint a mostani rész tárgyául szolgáló erős kölcsönhatáshoz rendelt gluonokra. A fénysebességű forgás koncepciója szerint a fermionok és bozonok tulajdonságai a részecskéket alkotó forgások szimmetriájára vezethetők vissza. Az S = 1 spinhez a tér lokális egytengelyű forgása tartozik, szemben az S = ½ spinű fermionokkal, ahol két egymásra merőleges tengely körül történik a forgás.

Hogyan értelmezhetjük fénysebességű forgásokkal a kvarkok törttöltését, és két alaptípusának (flavour): up (röviden u) és down (d) létezését. Miért lépnek fel épp harmadok a töltésekben: ±2/3e és ±1/3e, és miért épp három kvark alkotja a barionokat? Arra könnyebb válaszolni, hogy a leptonoknál és kvarkoknál miért létezik három generáció: ez értelmezhető a fénysebességű forgások generációnként növekvő frekvenciájával. A Standard Modell szerint a második generációban charm (c) és strange (s), a harmadikban top (t) és bottom (b) tartozik ugyanabba a típusba, mint az up és down kvark.

A forgásmodell felépítéséhez analógiát nyújtanak a húr rezgései. A két végén rögzített húr alaprezgése a fél hullám, de létrejönnek felharmonikusak is: egész hullám, másfél hullám stb. Erre rímelnek a kvantummechanikában a molekulavibrációk, ahol a vegyértékrezgéseket az n = 0, 1, 2 … kvantumszám jellemzi. Az n = 0 típusú oszcilláció feleltethető meg a húr alaprezgésének, amit zérusponti rezgésnek is neveznek, mert még alapállapotban se áll le az összekapcsolt atomok mozgása, és ezáltal megnövekszik a molekula energiája is. Ez eltér a kifeszített húrtól, amelyik nyugalomban van, amíg nem pendítjük meg. Az alapállapotú vegyértékrezgés térbeli eloszlásának egy maximuma van és nincs csomópontja, ebben a húr fél hullámához hasonlít. A gerjesztett n =1 molekularezgés viszont már két maximummal és egy csomóponttal, az n = 2 pedig 3 maximummal és 2 csomóponttal rendelkezik, akárcsak a húrrezgés felharmonikusai. 

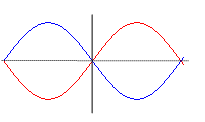
2. ábra. A rezgő húr három alap harmonikusa

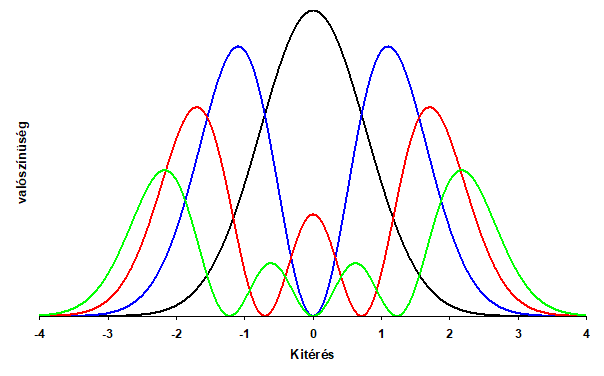
3. ábra. A kvantummechanikai oszcillátor pozíciójának valószínűségi eloszlása a kitérés függvényében, a görbék közül a fekete: n = 0, a kék n = 1, a piros n = 2, a zöld n = 3 kvantumszámhoz tartozik

2.2 . Oszcilláló forgások hármas szerkezete

Beszélhetünk-e hasonló gerjesztett állapotokról, ha nem oszcillációról, hanem forgásokról van szó? A rezgés és forgás kapcsolatba hozható, hiszen ha a forgómozgást az átmérőre vetítjük, akkor oszcillációkat kapunk. Azt kell tehát keresnünk, hogy milyen szerkezetű forgás vetülete felel meg az egyes n = 0, 1, 2 oszcillációknak?  Induljunk ki az egyszerű forgásból, amely folyamatosan körbeszalad! Itt a forgás vetületének közepén fellép egy maximum és nincs csomópont, akárcsak a húr fél hulláma esetén, vagy az n = 0 oszcillációnál. De bontsuk fel a körbejárást részforgásokra (hurkokra), mégpedig oly módon, hogy a mozgás során csomópontok, illetve maximumhelyek alakuljanak ki! Ehhez az kell, hogy az első részforgás félúton lépjen át egy másodikba, ami úgy valósulhat meg, ha az új hurok forgásiránya fordítottja lesz az előzőnek. Például, ha az első részforgás iránya megegyezik az óramutató járásával – jelöljük ezt „+” szimbólummal – akkor a második hurok mozgása már szembe megy az óra járásirányával, amit a „– ” szimbólummal jelölhetünk. Ez viszont azt jelenti, hogy a második részforgás félfordulat megtétele után szembemegy az alapforgással (lásd 4. ábra). Ilyen kételemű „+–” felbontás ezért nem lehetséges. Ki kell tehát zárni a lehetőségek közül a két részforgásból álló és egy csomópontos összetett forgásokat. Viszont, ha a második részforgás átmegy egy harmadikba, akkor a forgáskombináció a félfordulat után egyirányú lesz az alapforgással. Ebből az elvből következik, hogy az összetett forgásban csak páratlan számú hurok lehet, melyek közül a legegyszerűbb a háromhurkos „+–+” felbontás, amelyben két csomópont és három maximumhely található. A csomópontokat tartalmazó forgás koncepciója tehát összhangban van a barion típusú részecskék hármas szerkezetével. (Lehetne még 5 hurkos összetett forgás is, de erre csak akkor lenne szükség, ha a részecskék Standard Modelljében lennének 5 részecskéből álló barionok is.) Leptonokhoz (elektron, pozitron, neutrínó) képest az a döntő különbség, hogy a kvarkoknál nem ekvivalens a két forgás, és ez az aszimmetria új típusú kölcsönhatásokhoz vezet.

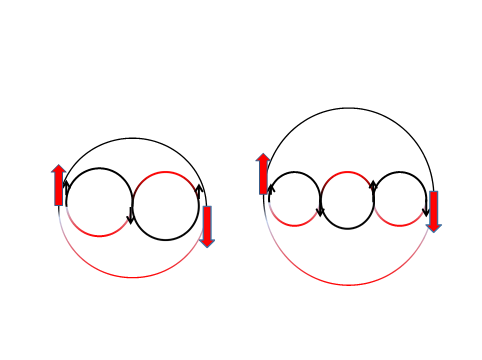
4. ábra. Balra: két hurokra, jobbra: három hurokra bontott forgás körüljárási iránya az egyszerű forgáshoz képest. A kéthurkos bontásban a félfordulat piros nyila fordított a feketéhez képest, míg a háromhurkosban megegyezek az irányok.

2. 3. Miért rendelkeznek a kvarkok törttöltésekkel?

Térjünk most rá a törttöltés eredetére! Az S = ½ spinű fermionokat kettős forgások hozzák létre, melyben nevezzük az egyik forgást X-nek, a másikat Y-nak. Csak a második, azaz Y forgás legyen összetett. A 4. ábrán a hurkokra bontást síkban ábrázoltuk, itt azonban az egyes hurkok síkja eltérő, mégpedig egymásra merőleges (Lásd 5. ábra).

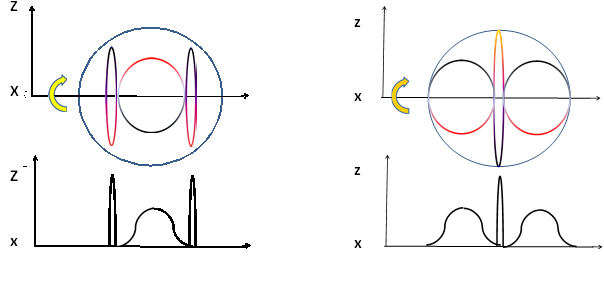
5. ábra. Baloldalon az xyx, jobboldalon az yxy típusú oszcillációs forgások láthatók, lent pedig a vetületek

Ez a geometria már értelmezi a törttöltéseket, mégpedig azáltal, hogy az Y forgás felbontásában szereplő egyes hurkok forgástengelye részben párhuzamos az X forgáséval (ekkor nincs Coriolis-erő), részben viszont merőleges X-re (ekkor van Coriolis-erő), és jelölje az előbbi tengelyt x, az utóbbit y. Ez a felbontás nem változtatja meg az S = ½ spint, vagyis az impulzusnyomatékot, mert a mozgás iránya végig merőleges marad a sugárra egyezően az egyszerű körforgással.

Két lehetséges forgáskombináció jöhet létre: (xyx), illetve (yxy), amit a fenti ábra mutat be. Az y hurkok száma adja ki a töltést, mert csak ott lép fel Coriolis erő, viszont ennek előjele a körüljárási iránytól, azaz a kiralitástól függ. Jelöljük „+” és „–” szimbólumokkal a körüljárási irányt, evvel négy forgáskombinációhoz jutunk: (x⁺y^–x⁺), (x^–y⁺x^–), (y⁺x^–y⁺) és (y^–x⁺y^–). Az egyes forgáskombinációk töltésének nagysága -1/3e, +1/3e, +2/3e és -2/3e lesz, megfelelve a d kvarknak és antikvarknak, illetve az u kvarknak és antikvarknak. Az összetett Y forgás körüljárási iránya azonos az első részforgás előjelével, és ennek megfelelően az Y⁺ és Y^– forgások reprezentálják a részecske és antirészecske kettősséget. Ugyanezt úgy is jelölhetjük, hogy felcseréljük az egyszerű X és az összetett Y forgások szerepét, amit YX típusnak nevezhetünk. Ekkor az Y forgás lesz az egyszerű, és az X forgás az összetett, és az XY, illetve YX kombinációk kvarkot, illetve antikvarkot jelölnek.

.

2. 4. Oszcillációk kötött rendszerekben

Kvarkokra javasolt mozgásformát oszcillációs forgásnak is nevezhetjük, mert az Y forgás három hurkának z-irányú kitérései oszcillációt alkotnak. A kvark oszcilláció összhangban van a kvantummechanika már említett törvényével, miszerint minden kötött rendszer zérusponti rezgés végez, azaz még alapállapotban is van oszcilláció.

Az állítás meg is fordítható: csak akkor alakul ki oszcilláció két objektum kötött, ha valamilyen vonzó erőhatás összeköti őket. A kvarkokból felépülő barionokban és mezonokban az összetartó erőt az erős kölcsönhatás hozza létre, ezért a bezártság elv, mely szerint szabad kvark, azaz törttöltés megfigyelése nem lehetséges, összhangban van avval a felfogással, hogy a kvarkok létrejöttét oszcillációs forgások idézik elő: ha nincs oszcilláció, akkor kvark sincs. Úgy is fogalmazhatunk, hogy a törttöltésű kvark egy alacsonyabb szimmetriájú részállapot (mintázat) a magasabb szimmetriájú összetett struktúra (barion és mezon) belsejében, és a „mintázat” szerkezetét a részecskét egyben tartó erős kölcsönhatás határozza meg. Ez az erő alakítja ki az oszcillációs forgásokat, melyben a pályamozgás során megváltozik a forgástengelyek iránya is.

2. 5. Mi a kvarkok színtöltésének eredete?

A kvarkelmélet meghatározza, hogy a mezonok és barionok szerkezete milyen kvarkkombinációkból épül fel. Vizsgáljuk meg, a felépítési elv hogyan teljesül a kéttengelyű forgások modelljében. Nézzük először a barionokat, amelyek a Standard Modell szerint vagy három kvarkból, vagy három antikvarkból épülnek fel. A barionok spinje lehet ½, vagy 3/2, ez a lehetőség a spinek szokásos összeadási szabályából következik. Mivel a barionokban vagy csak kvarkok, vagy csak antikvarkok vannak, és az előbbi töltése 2/3e, vagy  –1/3e, az utóbbié 1/3e, vagy –2/3e, így belátható, hogy csak az elemi töltés egész számú többszöröse jöhet létre (nulla, ±e és ±2e), amikor három részecske kapcsolódik össze. A kvarkoknak a töltésen és spinen kívül van azonban egy további szabadsági fokuk is: a színtöltés. Ez három különböző értéket (színt) vehet fel, ugyanakkor a belőlük felépülő barionok szín semlegesek, azaz a bariont felépítő három kvark, vagy antikvark különböző színű, amelynek eredője „fehér” lesz. Eddig XY típusú kvarkokról beszéltünk, de ugyanilyen joggal választhatunk YZ és ZX forgásokat is, ahol mindig az első az egyszerű, a második az oszcillációs forgás. Ezt a három forgáskombinációt rendelhetjük a kvarkok három színéhez, viszont a barionok színsemlegessége („fehér színe”) azt követeli meg, hogy a három kvarkban, vagy antikvarkban az XY, YZ és ZX, illetve YX, ZY és XZ forgástípusok egyenlő súllyal szerepeljenek. Ez gömbszimmetrikus (izotrop szerkezetű) barionok esetén teljesül.

A barionok összetételének még eleget kell tenni a Pauli-elvnek is, amely megköveteli, hogy kötött kvantumállapotban ne forduljon elő két olyan fermion, melyek minden kvantumszáma egyezik. Ez azt jelenti, hogy nem lehet két kvarknak mind a töltése, mind a spin vetülete (+½ és –½), mind a szín-kvantumszáma és még generációs indexe is azonos. Három azonos kvarkból álló barion azonban létrejöhet, például az (uuu), vagy (ddd) konfigurációk, éppen a kvarkok különböző színére vonatkozó szabály miatt. Megjegyezzük még, hogy az atommagokat felépítő két nukleon, a proton és a neutron összetétele: (uud), illetve (udd).

A hadronok másik csoportját a mezonok alkotják, amelyek egy kvarkból és egy antikvarkból épülnek fel. Töltésük szintén csak az elemi töltés égésszámú többszöröse lehet, mégpedig 0 vagy ±e. A kvarkokra felírt töltéskonvenció itt is kizárja törttöltésű mezonok létezését. A spin lehet 0, vagy 1, megfelelően annak, hogy bozonokról van szó. A mezonoknak sincs színük, amit az biztosít, hogy az antikvarkok színe a kvarkok színének komplementere. Ez megkívánja, hogy az XY és YX kombinációk színe egymás kiegészítője legyen.

2. 6. Hogyan forrasztják össze a kvarkokat a gluonok?

A Standard Modell 8 független gluonnal értelmezi a kvarkokat összekötő erős kölcsönhatást. A gluon szintén bozon, és spinje S = 1. A fénysebességű forgás koncepciója szerint egytengelyű forgás alkotja a bozonokat, amelyet kiegészít a forgástengellyel párhuzamos másik mozgás is. Ez a párhuzamosság felel meg annak, hogy a gluonoknak a fotonokhoz hasonlóan nincs elektromos töltésük, a gluonok viszont rendelkeznek színtöltéssel. De milyen lehet ez a másik mozgás, amely létrehozza a színtöltést?

Nézzük először, hogyan is közvetíti az erőhatást a foton két töltött részecske között a kvantumelektrodinamika szerint? A töltött részecskék virtuális fotonokat bocsátanak ki (emisszió) és nyelnek el (abszorpció), melynek polaritását a részecske királis szimmetriája határozza meg. Ez a folyamat véletlenszerű fluktuációkat hoz létre a részecske pozíciójában (vákuum fluktuáció), de nem mozdítja el. Ha viszont a virtuális foton egy másik töltött részecskéhez eljut és elnyelődik, akkor vagy meglöki azt, (ha a két töltés előjele azonos), vagy a két részecskét egymás felé húzza (ha ellentétes a töltések előjele). Így jön létre taszítás, vagy vonzás. A virtuális gluonok hatása ettől annyiban különbözik, hogy a gluon a színtöltésen át közvetíti a kvarkok közötti vonzást függetlenül a kiralitástól. A gluon kiralitás függetlensége abban nyilvánul meg, hogy nincs elektromos töltése. Két kvark összekapcsolásához viszont két különböző szín tartozik: az egyik a kibocsátó kvark színe, a másik az abszorbeáló kvark színének komplementere (az abszorpció a szín komplementerét igényli). A kvarkok színét a kér forgás különböző szerkezetére vezethetjük vissza. Például az XY oszcillációs kettősforgást, azaz kvarkot „y⁺” színűnek nevezhetjük, mert y irányban oszcillál a Coriolis-erő, és pozitív indexet használunk, hiszen kvarkról és nem antikvarkról van szó. Evvel szemben az YX antikvarkhoz az „x^–” komplementer színt rendeljük hozzá, az x irányú oszcilláció miatt. A negatív index jelöli, hogy komplementer színeknél az oszcillációs fázis fordított. Ezt az elvet követve vezethetjük be a YZ és ZX kvarkok esetén az „z⁺” és „x⁺” színeket, míg a ZY és XZ antikvarkoknál az „y ^–” és „z ^–” komplementer színeket. Összesen tehát három alapszínről es három komplementer színről beszélhetünk.

Kvarkok esetén az oszcilláló forgás és az egyszerű forgás között fellépő Coriolis-erő bocsátja ki a gluonokat, de ez sokkal erősebb az elektromos erőnél, minthogy a kvarkok közvetlenül érintkeznek a barionokban és mezonokban. Emiatt az erős kölcsönhatásban nem csökken le a ħc szorzattal arányos erő, és így mintegy 137-szer nagyobb lesz a vonzóerő, mint amit az elektromágneses kölcsönhatás létrehozhat. A kölcsönhatás ereje nem változik a barionok mérettartományán belül, viszont az atommagokban, ha nem érintkeznek a nukleonok, a kontaktus hiányában a vonzás gyorsan megszűnik.

2. 7. Gluonok osztályozása a Standard Modellben

Az elmondottak értelmében a gluon tehát irányokat (azaz színeket) összekapcsoló közvetítő részecske, amely az egyik irányú oszcillációt átviszi egy másik irányba, és evvel járul hozzá, hogy a magas szimmetriájú barionokban és mezonokban kialakuljanak alacsonyabb szimmetriájú „mintázatok”, azaz a kvarkok. A gluon ezért elválaszthatatlan tartozéka a két kvarkkonfigurációnak: a háromelemű barionoknak és a kételemű mezonoknak. Sem kvarkokat, sem gluonokat nem észlelhetünk szabadon, ezek a részecskék csak együtt létezhetnek az összetett részecskéken belül. Ez nyilvánul meg abban is, hogy nem tudunk valódi tömeget rendelni az egyes kvarkokhoz, csak renormált tömegekről beszélhetünk, hiszen a részecskék saját energiáját a kvarkok és gluonok együttesen alakítják ki.

A barionok három különböző színű kvarkból, vagy antikvarkból épülnek fel, ennek megfelelően a „színváltoztató” gluonok a következők lesznek:

(x⁺y^–), (x⁺z^–), (y⁺x^–), (y⁺z^–), (z⁺x^–), (z⁺y^–)

Mezonokban viszont a részecske színsemlegességét iránytartó (színtartó) gluonok hozzák létre, melyekben nem változik meg az oszcillációs irány, tehát a szín-kvantumszám, ezek pedig a következők:

(x⁺x^–), (y⁺y^–) és (z⁺z^–)

A negatív indexek jelölik, hogy a komplementer színek oszcillációs fázisa ellentétes a színekhez képest.

A kilenc gluon 3*3-as mátrixba rendezhető:

(x⁺x^–)   (x⁺y^–)   (x⁺z^–)

(y⁺x^–)   (y⁺y^–)   (y⁺z^–)

(z⁺x^–)   (z⁺y^–)    (z⁺z^–)

Összességében gömbszimmetrikus potenciáltér jellemzi hadronokban az erős kölcsönhatást. Ennek megfelelően a háromdimenziós mátrix felbontható a forgáscsoport egy-, három- és ötdimenziós ábrázolására, hasonlóan az L = 0, L = 1 és L = 2 gömbfüggvényekhez. Az L = 0 gluon kombináció szingulett állapotnak felel meg, amelynek létezését a Standard Modell kizárja, emiatt beszél az elmélet nyolc független gluonról. A háromdimenziós L = 1 függvénytér vektoriális, az L = 2 ötdimenziós függvénytér tenzoriális erőmezőt hoz létre.

2. 8. Összetett részecskék spinje és véges hatáskeresztmetszete

A pontszerűséggel kapcsolatban érdemes még kitérni arra a kérdésre is, hogy a proton töltéseloszlása a mérések szerint nem pontszerű, bár az elektronhoz hasonlóan a spinje ½. Az elektron impulzusnyomatékát a fénysebességű kettős forgásra vezettük vissza, ezért ha evvel magyaráznánk a proton spinjét is, akkor nulla hatáskeresztmetszetet várnánk a szóráskísérletekben. Ha nem tudnánk az elméletből, hogy a proton három kvarkból épül fel, akkor már a véges hatáskeresztmetszet létezéséből levonhatnánk a tanulságot, hogy a proton összetett szerkezetű! Mivel a valóban elemi – tehát tovább nem osztható – fermionoknak a kettős forgás koncepciója szerint ½ a spinje, így a spinek összeadási szabályából már következik, hogy legalább három komponensből épül fel a proton, ugyanis két ½ spin összege nulla, vagy egy lehet. Egyébként az összetett részecskék családjában vannak két kvarkra bontható mezonok is, ahol tényleg a spin 0, vagy 1 értéket vesz fel. Három ½ spin alkothat akár ½, akár 3/2 spint is. Léteznek ennek megfelelően olyan barionok is, melyeknek spinje 3/2.

2. 9. Az atommagokat összetartó erő

Az atommagok felépítése további kérdést vet fel: milyen erő köti össze benne a nukleonokat, az (uud) szerkezetű protont és az (udd) neutront. Ez a kvarkokat összekötő erős kölcsönhatás másodlagos hatása, amit a kvantummechanika kicserélődési erőnek nevez. Ez akkor jön létre, ha két összetett objektum, például két atom a molekulában, vagy esetünkben a nukleonok az atommagban, egymás között felcserélik „alkatrészeiket”. A molekulák atomjaiban az elektronok, az atommagban a kvarkok „szabadon járnak-kelnek” a nukleonok között. Precízebben szólva az elektronok, illetve a kvarkok egyidejűleg több objektumban is megtalálhatók bizonyos valószínűséggel. Ez a kicserélődési kölcsönhatás, amely valamennyi fermion alaptulajdonsága, melynek szabályait a Pauli-féle kizárási elv adja meg. Molekulákban például ez az atomokat összekapcsoló kovalens kötés alapja. A kvarkok „átjárásához” a nukleonok közvetlen érintkezése szükséges, ami magyarázza, hogy miért olyan rövidtávú a nukleonokat összekötő vonzóerő.

2. 10. Áttekintés a kvarkok és gluonok világáról

Végül is, milyen képet alkossunk a gluonok és kvarkok világáról?  Képzeljük el úgy a hadronokat (a barionok és mezonok összefoglaló neve), amelyek kívülről gömbszimmetrikusok, de van egy belső szerkezetük is, amit kvarkoknak nevezünk. Mindegyik kvark egy-egy fénysebességű kettős forgás, melyekből az oszcilláló Coriolis-erők körforgásokat indítanak meg felületükön, és ezek összekötő rugóként kapcsolják egymáshoz a kvarkokat. Ezt nevezzük erős kölcsönhatásnak. A körforgások és oszcillációk összetett struktúrája alakítja ki a gluonok kettős színvilágát. Ez a színvilág a hadronon kívül már nem látszik, mert kifelé a hullámzás már gömbszimmetrikus pulzálást idéz elő, ami avval is együtt jár, hogy a hadronok töltése az elemi töltés egész számú többszöröse lesz. Törttöltésű részecske szabadon nem figyelhető meg, mert a gluonok építik ki azokat a több hurkos forgási állapotokat, amelyek megformálják a kvarkokat. A belső mozgásformák spontán módon képesek átrendeződni és kialakíthatnak újabb forgáskombinációkat, miközben kibocsátanak egyéb mozgásformákat is: elektronokat és neutrínókat. Ezeket az átalakulásokat a gyenge kölcsönhatás vezényli le, amivel majd a következő részben foglalkozunk.

Ennek a résznek fő mondanivalója, hogy fénysebességű kettős forgásokkal jól lehet szemléltetni az erős kölcsönhatás jelenségeit is.

Következő rész:

A blog további írásai: "Paradigmaváltás a fizikában"