-
3. Látogatás a részecskék szerelőműhelyében: a gyenge kölcsönhatás
Az előző két részben (első, második) azt kerestük, hogyan találjuk meg a kapcsolatot a gravitáció, az elektromágnesség és az erős kölcsönhatás között a fénysebességű forgások koncepciója alapján. Ez a közös alap nem a mezőelméletek alapelve, a kvantum volt, hanem a tér forgásai. Amíg ez a forgás fénysebességgel megy végbe az elektromágnesességet közvetítő fotonok és az erős kölcsönhatás gluonjai esetén, a gravitáció kettős forgásai lassulnak a távolsággal a Kepler szabály szerint, és messze elmaradnak a fénysebesség mögött. A közvetítő eszköz tehát nem a szokásos bozon a gravitációnál, amihez S = 1 spint rendelhetünk, hanem egy láthatatlan – ha úgy tetszik virtuális – forgás, amit formálisan S = 0 spinnel jelölhetünk. A részecskét alkotó fénysebességű kettős forgások bocsátják ki ezeket a lassú gömbhullámokban terjedő forgásokat, melyek emissziós és abszorpciós egyensúlya alakítja ki a gravitációs potenciált a térben okozott görbületek révén.
Ebben a záró részben tesszük meg a következő lépést, amelyben megvizsgáljuk, hogyan alakulnak át egymásba az elemi részecskék a gyenge kölcsönhatás által, és milyen szemléletes képet tud adni erről a fénysebességű forgások koncepciója. Ez a rész jelentős mértékben „A rejtélyes gyenge kölcsönhatás” című korábbi íráson alapul.
-
1. Két kölcsönhatás eltérő világa
Aligha lehetne két jobban eltérő kölcsönhatást találni, mint az elektromágneses és a gyenge kölcsönhatás. Az elektromágnesesség közvetítője a foton akár milliárd fényév távolságból is megérkezhet hozzánk egy távoli galaxisból, szemben a gyenge kölcsönhatást közvetítő W és Z bozonokkal, melyek hatótávolsága az atommagnál is kisebb, úgy 10–16 m nagyságába esik. Elmondható ez az élettartalmukról is, a távoli galaxisokból érkező foton milliárd éves utazás után is megfigyelhető, míg a W bozon élettartama nem hosszabb 10–24 másodpercnél. Szintén nagyon eltérnek tömegükben és töltésükben is, a fotonnak nincs is nyugalmi tömege, míg a két gyenge kölcsönhatási bozon a részecskevilág nehézsúlyú bajnoka, ha eltekintünk a Higgs bozonnak tulajdonított részecske tömegétől, akkor valamennyi megfigyelhető részecske tömegét meghaladja a W és Z bozoné. Ami pedig a töltésüket illeti, a fotonnak nincs töltése, viszont a W bozonnak van, mégpedig a +e illetve –e elemi töltés, hasonlóan az elektronhoz és a pozitronhoz. A W+ és W– egymás részecske-antirészecske párja, míg a fotonok világa nem ismeri ezt a kettősséget. Abban is nagy a különbség, hogy amíg az elektromágneses erőhatás vonzás, vagy taszítás két objektum között, addig a gyenge-kölcsönhatás szerepe, hogy átalakítsa a részecskéket egymásba. Abban is különböznek, hogy az elektromágneses kölcsönhatás csak töltött objektumokra hat, viszont a gyenge kölcsönhatásban minden részecske részesül. Csupán egy dologban egyeznek: spinjük egyaránt S = 1, azaz bozonokról van szó. Másrészt viszont sokkal nagyobb a hasonlóság az elektromágnesesség és a gravitáció között, nézzük akár az időtávot, vagy a kölcsönhatások távolságfüggését. Ezért hatott a fizikus társadalomban meglepetés erejével, hogy a gyönge és elektromágneses kölcsönhatás közös elméleti alapra helyezhető (elektrogyenge kölcsönhatás), míg a gravitáció nem volt bevonható az egyesített mezőelméletbe (Sheldon Glashow. Steven Weinberg, Abdus Salam, Nobel díj: 1979).
-
2. Az átalakulások megmaradási elvei
A gyenge és elektromágneses kölcsönhatás eltérésének és ugyanakkor mélyen fekvő hasonlóságának megértéséhez szemléletes kulcsot ad a részecskék fénysebességű forgásmodellje. Először azt kell megértenünk, hogy milyen állapotváltozást hoz létre a két kölcsönhatás. Az elektromágnesesség hatását legkönnyebb az elektron példájával szemléltetni. Az atomban, vagy molekulában kötött elektron pályáját az impulzusnyomatékkal jellemezhetjük, melynek értéke a redukált Planck-állandóval fejezhető ki: Lℏ, ahol az L egész szám a pályamozgás kvantuma. Az elektron állapotváltozása során az L kvantumszám eggyel változik, legyen szó foton elnyelésről (abszorpció), vagy kibocsátásról (emisszió). Ilyenkor az elektron pályaugrása hozza létre, vagy tünteti el a foton S = 1 spinjét, azaz annak ℏ nagyságú impulzusnyomatékát. Szemléletesen úgy mondhatjuk, hogy az elektron „keringő” mozgása konvertálódik a foton saját forgásává. Hasonló magyarázat adható, amikor értelmezzük mágneses mezőben Larmor-precessziót végző S = ½ spinű elektronok rezonancia átmeneteit, ekkor a foton abszorpciója, vagy emissziója során a spin mágneses mező irányú komponense egységnyit változik (szokásos jelölésben Sz értéke +½ és ̶½ között ugrik). Ebben az esetben a mágneses mezőben polarizált elektronspin megváltozása biztosít forrást a foton impulzusnyomatékához. Mindkét esetben az energiamegmaradás mellett az impulzusnyomaték megmaradása vezet a kvantumátmenetek kiválasztási szabályához. Ehhez még hozzá kell tenni, hogy az átmenetek során az elektronok nyugalmi tömege ugyanannyi marad.
-
3. Annihiláció és párképződés
Létezik egy másik kapcsolat is a fotonok és a részecskék között, az annihiláció és a párképződés. Az előbbi esetben egy azonos tömegű részecske és antirészecske eltűnik gamma-sugárzás létrejöttével, a másik folyamat ennek fordítottja, amikor létrehoz a foton egy részecske-antirészecske párt, például egy elektront és egy pozitront. Az utóbbi folyamathoz szükséges egy „ütköző” atom is az impulzusmegmaradás miatt. Ezek a folyamatok mutatják, hogy a nyugalmi tömeg képződhet is, meg el is tűnhet, vagyis a nyugalmi tömeg a mikro folyamatokban nem megmaradó mennyiség. Az átalakulások kiválasztási szabálya viszont, hogy az energia, a töltés és a spin (impulzusnyomaték) megmaradjon. Mivel a fotonnak nincs töltése, ez a szabály azt jelenti, hogy a képződő két részecske ellentétes előjelű töltéssel rendelkezik, másrészt a foton S = 1 spinje megköveteli, hogy a két új részecske egyaránt ½ spinnel rendelkezzen. A fénysebességű forgásmodellben a feltétel azáltal teljesül, hogy az elektron és pozitron kettős forgásának ellentétes a kiralitása, és így az annihiláció során kioltódik az egyik forgás az ellentétes sodrásirány miatt, miközben a másik forgás mindkét részecskénél megmarad, ez a megmaradó forgás pedig nem más, mint két gamma foton. A kettős forgás egyik komponensének megszűnéséhez az is kell, hogy a frekvenciák megegyezzenek, azaz csak két azonos nyugalmi tömegű részecske és antirészecske semmisítheti meg egymást. Párképződéskor viszont megfordul a helyzet, ekkor a fénysebességű haladó mozgás két ellentétes perdületű forgásra hasad fel, amiért a képződő kettős forgások kiralitása, azaz töltése ellenkező előjelű lesz, a foton ℏ impulzusnyomatéka pedig két egyenlő részre válik szét.
-
4. Leptonok
3.4.1. Az elektroncsalád tagjai
Térjünk át a részecskeátalakulások megmaradási szabályaira! Nézzük meg ehhez az elektron (e) és „nagy testvérei” a müon (μ) és a tau részecske (τ) esetét! Ezek a töltött leptonok, amit „anyagnak” nevezünk, ha a töltés negatív, és „antianyagnak”, ha pozitív. Szintén a leptonok közé tartoznak a töltéssel nem rendelkező neutrínók (ν). Ebben a „családban” a töltés és a spin azonos, viszont a nyugalmi tömeg erősen különbözik, a müon tömege 207-szer, a tau részecskéké 3477-szer nagyobb az elektronhoz képest. (A három részecske energiája: 0,511 illetve 105,66 és 1776,8 MeV.) Honnan származnak ezek az arányok? Erre a részecskék tulajdonságait összegző Standard Modell sem adja meg a választ, ezért ezeket az értékeket fogadjuk el, mint kísérleti tapasztalatot. A két nehezebb részecske viszonylag rövid életű szemben a stabilis elektronnal: müon: 2,2x10–6 s, tau: 2,9x10–13 s, és bomlásuk egyik végterméke az elektron. A részecskevilágban ez az élettartam nem számít rövidnek, mert amikor gamma-sugárzás jön létre más részecskék bomlásakor, a tipikus felezési idő 10̶–20 s. A viszonylag lassú bomlás oka, hogy leptonoknál egyedül a gyenge kölcsönhatás játszik szerepet, mert itt az elektromágneses átmenet tiltott.
3.4.2. Neutrínók a konzekvens kvantummechanika tükrében
Hogyan lehet a másik leptont, a neutrínót is leírni fénysebességű forgásokkal? Ehhez kölcsön kell venni a kvantummechanikából a szuperpozíció elvét. Ez kimondja, ha valamilyen mikro objektum mozgását két független szimmetrikus pálya – azaz állapotfüggvény – jellemzi, akkor ezek szuperpozíciója is az energiaoperátor sajátfüggvénye lesz. Ha nincs jelen külső elektromos mező, akkor az elektron és pozitron energiája is azonos, mert csupán a királis szimmetriában térnek el. A fénysebességű forgás koncepciója a tér lokális kettős forgásaival azonosítja a fermionokat, ezért az elektron és pozitron kettős forgásaiból kialakulnak különböző lineáris kombinációk. Ha a két királis forgás részaránya egyenlő, akkor az ellentétesen oszcilláló Coriolis erők semlegesítik egymást, és így a mozgási állapotnak nulla lesz a töltése, vagyis nem hat rá az elektromágneses kölcsönhatás. Ez a mozgásforma a neutrínó, amit rendkívül nehéz megfigyelni, mert csupán a gyenge kölcsönhatás révén ad hírt magáról. De ugyanígy a müon és antimüon, illetve a tau és antitau részecskék is alkothatnak semleges töltésű szuperpozíciót, ezért három különböző neutrínóról beszélhetünk.
A neutrínók elmélete több nyitott kérdést vet fel. Az egyik ilyen, hogy létezik-e antineutrínó, vagy pedig a neutrínó önmagának az antirészecskéje. A másik, hogy a kísérletek tanúsága szerint a neutrínó sebessége egyezik a fénysebességgel a mérési pontosság határain belül, ugyanakkor a három neutrínó között oszcilláció lép fel a fluxus vizsgálatok szerint. Ugyanis a különböző égi objektumból érkező neutrínó fluxus kisebb, mint amit az elmélet megkíván, és ez magyarázható, ha oszcilláció jön létre a három típus között. A fénysebességű mozgás viszont csak nulla tömegű részecskék számára lehetséges, de akkor miben különbözik a neutrínó három típusa? Ezekre a kérdésekre keresi a választ a konzisztens kvantummechanika felvetése: (Antal Rockenbauer: „Consequent Quantum Mechanics by Applying 8-Dimensional Spinors in the Dirac Equation”, Physical Science International Journal, 2020, 24, 27-31). Az elképzelés abból indul ki, hogy amíg a szokásos kvantummechanika az energiához, impulzushoz és impulzusnyomatékhoz operátorokat rendel, addig a töltést és tömeget mint konstansokat kezeli. Kiindulva a relativitáselmélet kovariancia törvényéből, amely az energia négyzetét az impulzustag és a nyugalmi energia négyzeteként állítja elő, a publikáció bemutat egy olyan lehetőségét, amikor a Dirac által javasolt négydimenziós spinor felbontás helyett a négyzetgyökvonást nyolcdimenziós spinorokkal végezzük el, ahol már a töltést és a tömeget is a spinhez hasonló operátorok írják le. A módszer olyan általános fermion egyenletet eredményez, amelyben az elektront, az up és down kvarkokat, valamint a neutrínókat, egyaránt le lehet írni egy új kvantumszámmal, amely az elemi töltés háromszorosa. A neutrínók sajátsága ebben a leírásban, hogy jól definiált impulzussal rendelkeznek, viszont tömegük várhatóértéke nulla, akárcsak a fotonnak. Ez már lehetővé teszi, hogy a neutrínók a fotonhoz hasonlóan fénysebességgel haladjanak, miközben különböző impulzusuk miatt oszcillálhatnak is. Az alkalmazott formalizmus szerint nincs külön antineutrínó, azaz a neutrínó önmagának az antirészecskéje.
Kvarkok esetén a két királis állapot súlyaránya eltérő, amit az erős kölcsönhatás idéz elő. A kiralitás eltérő mértéke értelmezi a törtöltéseket, és magyarázza, hogy ilyen részecske szabadon nem figyelhető meg, mert képződésük alapfeltétele az erős kölcsönhatás, ami viszont szabad állapotban nincs jelen.
-
5. A gyönge-kölcsönhatási bozon spirálmozgása
Az előző pontban említettük, hogy a müon és a tau részecske nem stabilis, és a bomlás során elektron jön létre neutrínók kíséretében. Az első kérdés, ami felmerül, hogy miért nem gamma-sugárzás kibocsátásával megy végbe az átalakulás, hiszen ekkor sem a spin megmaradás, sem a töltésmegmaradás szabálya nem sérülne (a töltés nem változik, a spin vetületi kvantumszám ugrását ½ és –½ között pedig kiegyenlíti a foton S = 1 spinje). Az ilyen átmenet tiltását a részecskék fénysebességű forgásmodelljével értelmezhetjük. A foton egytengelyű forgás, amely a fermion kéttengelyű forgása közül csak az egyiket tudja megváltoztatni. Ahhoz, hogy mindkét forgási frekvencia megváltozzon (a müon és tau csak a forgási frekvenciában tér el az elektrontól!), két lépésre van szükség. Első lépésben a gyenge kölcsönhatás a töltést és a tömeget az egytengelyű forgásnak adja át (W- bozon, S = 1), de létrehoz egy töltés semleges és tömeggel nem rendelkező fermiont is (neutrínó, S = ½), amely a kettősforgás jelleget viszi tovább. Az impulzusnyomaték megmaradási törvényét, amit a spinek összegzési szabályai írnak le, úgy is felfoghatjuk mint a forgások számának megmaradási törvényét. A tau részecske bomláskor beszélünk tau neutrínóról, müon bomláskor müon neutrínóról, míg az elektron neutrínó az elektronok képződésében játszik szerepet.
A bomláskor képződő W bozon tehát jelentősen különbözik a fotontól, hiszen átveszi a müon töltését és van jelentős tömege is, mégpedig jóval nagyobb a tömege, mint amekkorával a kibocsátó fermion rendelkezett. Ezt úgy foghatjuk fel, hogy rendkívül rövid időre – ez a már említett 10-24 s – létrejön a térben egy akkora görbület, amelynek potenciális energiája ellentételezi a W bozon képződési energiáját. Mivel a W bozon egytengelyű forgás, csak úgy lehet töltése, ha a forgáshoz olyan haladó mozgás kapcsolódik, amely merőleges a forgási tengelyre, ez ugyanis a Coriolis-erő fellépésének feltétele. Ez a másodlagos mozgás a forgási sugarat fénysebességgel növelni fogja, ami spirális kialakulásához vezet, ahol a sugárnövekedést az r = r0 + ct összefüggés írja le. Itt r0 = h/m0c a W bozon Compton-sugara. Az ω körfrekvenciájú forgás kerületi sebessége c = ωr, ezért a sugárnövekedés a körfrekvencia csökkenésével jár az

egyenlet szerint, ahol az ω0 frekvencia a W bozon m0 tömegéből számolható a ℏω0 = m0c2 ekvivalencia elv alapján. A frekvenciacsökkenés a tömeg, illetve a részecske energiájának csökkenését hozza magával. A W bozon kísérletileg meghatározott tömegét ezért lokális képződési tömegnek kell tekinteni és nem nyugalmi tömegnek, hiszen a fénysebességű terjedés miatt a kölcsönhatási bozon nem lehet nyugalomban. A fotontól eltérően mégis jogunk van tömegről beszélni, mert a W bozon energiája és az ennek megfelelő E/c2 tömege a tér egy szűk tartományára lokalizálódik. (Itt érdemes utalni rá, hogy a W és Z bozonoknak nem a tömegét, hanem az energiáját lehet mérni a nagy energiájú proton-proton ütközések során képződő részecskék detektálásával). A W bozon fokozatosan csökkenő körfrekvenciája teszi lehetővé, hogy a részecske átalakítás „csavarkulcsa” legyen, mert rezonanciába léphet a különböző tömegű – azaz forgási frekvenciájú – részecskékkel.
-
6. Impulzus szerepe az átalakulásban
A gyenge kölcsönhatások által vezérelt átalakulások mellékterméke a neutrínó, amit a folyamat „hulladék anyagának” tekinthetünk. Szerepük kettős, egyrészt az impulzus, másrészt az impulzusnyomaték megmaradási törvényének tesznek eleget. Ez előbbi szempontjából fontos, hogy noha a neutrínónak nincs tömege, impulzusa mégis van. A gyenge kölcsönhatás által előidézett átalakulás első lépésében, amikor a W bozonnal együtt egy neutrínó is kilép, a két részecske impulzusának összege nulla, azaz a neutrínó a W bozon meglökésével tesz szert impulzusra. Mivel fénysebességű mozgásról beszélünk, ez a saját impulzus a pc = E összefüggésből határozható meg, hasonlóan a fotonhoz. Az impulzus viszont irányfüggő mennyiség, ezért a meglökött W bozon mozgásának kitüntetett iránya lesz. Ez a polarizációs irány játszik fontos szerepet az átalakítási folyamat második lépésében. Ez a lépés az első fordítottja, ekkor a W– bozon átalakul elektronná egy második neutrínó kibocsátása mellett, de ez már jóval kisebb energiával történik, mert a spirálmozgás során a körfrekvencia lecsökkent. De mekkora ez a csökkenés? Nézzük meg a forgás fázisának változását, amit a frekvencia változása miatt integrálással határozhatunk meg:
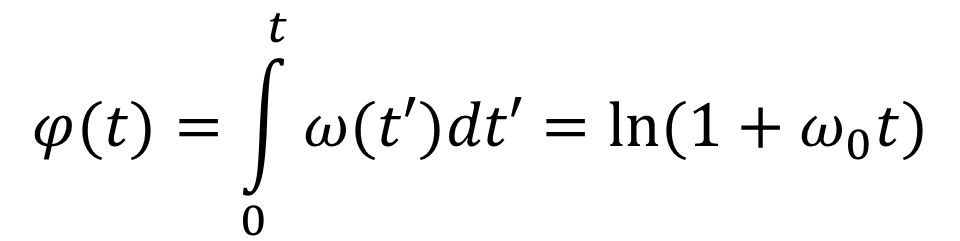
A fázis változását a sugár függvényében logaritmikus skálán mutatja a 6. ábra.
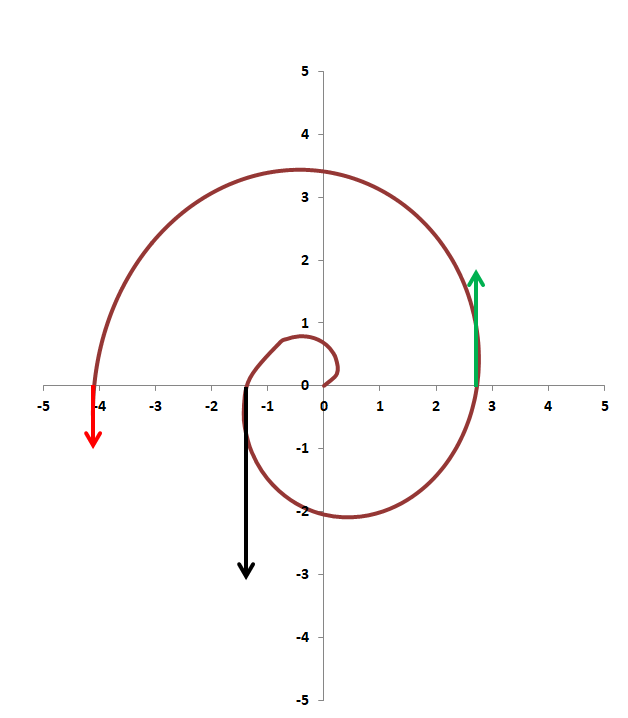
![]()
ábra. A W bozon spirális pályája logaritmikus ábrázolásban, a vastag nyíl az eredeti polarizációs irány, a fekete a tau, a zöld a müon, a piros az elektronkilépés irányát mutatja
-
7. A W bozon aktív fázisai
A következő kérdés, hogy a spirálmozgás milyen fázisánál következik be a második lépés, amikor képződik a két lepton? A spirálmozgás során fokozatosan csökken a W bozon energiája, ami végbemehet, mert a tér görbülete – és így a kiegyenlítő negatív potenciális energia – evvel együtt csökken. A W bozon azonban nyomtalanul nem tűnhet el, mert ekkor sérülne az impulzusnyomaték és a töltés megmaradási törvénye. Létezik azonban három „kijárat”, amikor képződik a két lepton, felhasználva a töltést és az impulzusnyomatékot is. Ezt a kijáratot a W bozon kezdő iránya szabja meg: akkor jön létre átalakulás, amikor egy-egy félfordulat végbemegy, ugyanis ekkor az impulzus újra az eredeti iránnyal lesz párhuzamos. Ennek megfelelően bármelyik π szögű elfordulásnál létrejöhet a két lepton. Vezessük be a ρ = 1 + ω0t tömegcsökkenési arányt, amely π szögű elfordulásnál eπ = 23,14 nagyságú lesz. Ez azt jelenti, hogy amikor az eredeti tömeg ilyen mértékben csökken, bekövetkezhet a W bozon átalakulása. Ezt is szemlélteti a fenti ábra. A W bozon induló energiája E0 = 80,395 GeV a mérések szerint, ez lecsökken az első félfordulat után Eπ = 3,4738 GeV, a másodiknál E2π = 150,1 MeV, a harmadiknál E3π = 6,487 MeV értékre. Ezen az energián osztozik a létrejövő két fermion. Rendeljük a tau, müon és elektron, valamint a megfelelő neutrínókhoz az n = 1, 2, 3 kvantumszámot, az előbbieknél az mn nyugalmi tömegből, az utóbbiaknál a pn saját impulzusból számíthatjuk ki az energiát:
Enπ = mnc2 + pnc
Az összefüggés lehetőséget ad, hogy a neutrínók három típusának megbecsüljük sajátenergiáját, feltételezve, hogy az elektron típusú részecskék kinetikus energiája elhanyagolható. A W bozon eltűnése után visszaáll az eredeti energia (helyreáll az energiamegmaradás szokásos törvénye, amely nem veszi számításba a tér potenciális energiáját), ezért az határozza meg, milyen részecske szabadul ki a W bozonból, hogy melyik saját energiája van közel a félfordulatok Enπ értékéhez. Mivel a tau részecske energiája 1,77682 GeV, azaz Eπ fele, így ez a részecske a W bozon első félfordulatánál jöhet létre, ekkor a tau neutrínóra jutó energia maximum 1,697 GeV lehet, tehát a két képződő részecske közel egyformán osztozik a bozon Eπ energiáján. A müon saját energiája 105,658 MeV, ezért ez már egy teljes fordulat után jön létre, a müon neutrínóra jutó energia pedig 44,44 MeV lesz, tehát kisebb, mint a müon saját energiája. Végül az elektron, melynek sajátenergiája 0,511 MeV, a harmadik félfordulat után jön létre, és ekkor a neutrínóra jut a W bozon maradék energiájának nagyobb hányada: 5,976 MeV. A nagyságrendi változásból látható, hogy a tau, müon és elektron tömege azonos ütemben csökken a W bozon félfordulatainak energiaveszteségével. A harmadik félfordulat a W bozon utolsó „kijárata”, mert az elektron stabilis részecske és spontán módon nem bocsát ki újabb W bozont.
-
8. Hadronok bomlása
Leptonok bomlásánál lényegesen bonyolultabb a kvarkokból felépülő mezonok (kvark + antikvark) és a barionok (három kvark, vagy három antikvark) bomlási mechanizmusa. Ennek egyrészt azaz oka, hogy a kvarkok a hadronok belsejében nincsenek sem tömeg, sem impulzus sajátállapotban, amelyben jól definiált sajátértékkel rendelkeznének, másrészt az összetett hadronokban (ez a barionok és mezonok összefoglaló neve) az erős és az elektromágneses kölcsönhatás is fontos szerepet játszik a gyenge-kölcsönhatás mellett. A kvarkoknak két típusa van a 2/3e töltésű u, és a –1/3e töltésű d, és a leptonokhoz hasonlóan három generációjuk létezik, melyek csak a tömegükben különböznek (pontosabban a renormált tömegükben, mert szabad kvark nem figyelhető meg). Az u típus két magasabb generációja a c és a t kvark, a d típusé az s és a b nevű kvark. A kvarkok három generációjának renormált tömege nagyságrendileg igazodik a W bozon három aktív állapotához: u és d az E3π, c és s az E2π, míg b az Eπ energiával összemérhető nagyságú. Kilóg a sorból a t kvark, amelynek nagy tömege meghaladja a W bozonét, evvel függhet össze, hogy olyan hadron nem is létezik, amelynek t kvark lenne az egyik összetevője.
-
9. Béta-bomlás
Hadronok közül az számít kivételnek, amelyben a gyenge kölcsönhatás hozza létre a bomlást, ennek oka, hogy az elektromágnesesség által előidézett bomlás ennél 10 nagyságrenddel gyorsabb. Ezért amikor a két kölcsönhatás együtt játszik szerepet, a gyenge kölcsönhatás részesedése nem becsülhető meg. Barionok közül a két nukleon (proton és neutron) különösen stabil: a proton (uud) spontán módon nem is bomlik fel, csak neutrínó-, vagy gamma-sugárzással alakítható át, míg a neutron (udd) bomlásának felezési ideje rendkívül hosszú: 880 s. A proton stabilitását az okozza, hogy a barionok közül ez a legkisebb saját energiával rendelkező részecske, neutron pedig azért stabilis, mert az elektromágneses kölcsönhatás nem idéz elő spontán bomlást. Ennek oka, hogy a gamma-sugarak nem rendelkeznek töltéssel, és így más részecskék töltését sem változtathatják meg, legfeljebb részecske-antirészecske párokat hozhatnak létre, ha elég nagy az energiájuk. A neutron spontán béta-bomlásakor proton jön létre, amelyet elektron és (anti)neutrínó kibocsátása kísér, magasabb generációhoz tartozó fermionok nem léphetnek ki, mert a neutron és proton közötti 1,3 MeV energiakülönbség nem elegendő müonok létrehozásához. Bár a képződő W bozon tömege elég nagy, de mindig úgy bomlik, hogy utána a szokásos energiamegmaradási törvény újra érvényes lesz. A béta-bomlás tehát kvark-kvark átalakítási folyamat W– bozon közvetítésével:
u → d + W–→ d + e– + νe
-
10. Mezonok bomlása
A mezonok családjában az ud összetételű (az aláhúzás jelöli az antikvarkot), +e töltésű pion a legstabilabb, melynek tömege 139,6 MeV/c2, a legkisebb a mezonok közül. Ez a tömeg egyrészt összemérhető a W bozon E2π energiájával, másrészt nagyobb a müon tömegénél, ami magyarázza a kvark kombináció átalakulását müonra és neutrínóra:
ud → W+ → μ+ + ν
Ekkor a gyenge-kölcsönhatás a kvark-antikvark kombinációt alakítja át leptonokra. Hasonló bomlási folyamata van az us összetételű +e töltésű kaonnak is, ahol a 493 MeV sajátenergia szintén elegendő müon részecske generálásához.
A gyenge kölcsönhatás által generált átalakításoknak csak egy részére tértünk ki. A Standard Modellben vizsgált nagyszámú átalakulásnak vannak egyéb kiválasztási szabályai is, ami további kvantumszámok megmaradásához kapcsolódik (gyenge izospin, gyenge hipertöltés). A komplex forgásállapotok játékszabályainak ismertetésére más alkalommal kerül majd sor.
-
11. A W bozonokat generáló Euler-erő
Az Euler tehetetlenségi erőről korábban már volt szó, amely fontos szerepet játszik a fermionokból kilépő forgások képződésében. Ennek forrása a fermionokat alkotó térforgás megszűnése a részecskék határánál. Ez a határ azonban nem lehet egyetlen matematikai pont, mert akkor végtelenül nagy lenne az Euler-erő. Véges szélességű héj létezése a kvantummechanikai bizonytalansági elv speciális következményének is tekinthető: a sugár R hosszának bizonytalansága a részecske p impulzusának végességéhez kapcsolódik a pxr = ħ összefüggés miatt.
Az Euler-erő a forgómozgás érintőjének irányába mutat, összhangban avval a képpel, hogy a képződő egytengelyes forgáshoz kapcsolódó haladó mozgás – ellentétben a fotonnal, ahol a haladási irány párhuzamos a tengellyel – ekkor a forgás síkjában lesz.
Az erő nagyságát az határozza meg, hogy mekkora annak a tartománynak a szélessége, ami alatt a részecske M tömegét meghatározó forgási frekvencia nullára csökken le. Az innen számolható Euler-erő a fénysebességű forgás modellben:
FEuler = ħc/RΔR
Itt ΔR a fermionok héjvastagságát jelöli, ami természetesen jóval kisebb, mint a részecske R = ħ/Mc Compton-sugara. Abból a tényből, hogy valamennyi részecskeátalakulási folyamatban ugyanakkora tömegű W bozon jön létre, arra kell következtetni, hogy fermionokban a gyenge kölcsönhatást generáló Euler erő azonos, vagyis minden fermionban megegyezik a héjvastagság RΔR keresztmetszete. Mivel az R Compton-sugár a tömeggel fordítva arányos, így a héjvastagság annál nagyobb, minél nagyobb a tömeg. A vastagság nem haladhatja meg a sugarat, ezért a gyenge kölcsönhatás kijelöl egy maximális tömeget. Ezért annak oka, hogy a mikrorészecskéknek nem lehet bármekkora tömege, visszavezethető a gyönge kölcsönhatása szétbontó szerepére. Úgy is fogalmazhatunk, hogy a térnek a görbülési képessége véges, mert egy határ fölött már nem tudja féken tartani az Euler-erőt. Vagyis a térnek a fénysebesség mellett létezik egy másik átléphetetlen határa is: a legkisebb görbületi sugár, amelynél kisebb tartományba már nem préselhető be fizikai objektum. Ennek a határnak felel meg a W bozon tömege, ahonnan a R = ΔR egyenlőséget feltételezve kapjuk meg a részecskék minimális görbületi sugarát:
Rmin = 2,456·10-18 m
A 173 GeV/c2 tömegű top kvark sugara ennél már kisebb lenne, ami magyarázza, hogy nem figyelhető meg olyan hadron, amelyben a top kvark is jelen lenne.
A kis héjvastagságból fakadó nagy Euler-erő azt is magyarázza, hogyan tudnak a W bozonnál jóval kisebb tömegű fermionok kibocsátani náluk több nagyságrenddel nehezebb kölcsönhatási bozont. Összehasonlítva a héjvastagságot az elektron Compton-sugarával, ez 157 330-szor kisebb, míg müonnál az arány 761 és a tau részecskénél 45,25. Az elektron stabilis részecske, a müon és tau elbomlik W bozonná és egy neutrínóvá
2,2·10-6, illetve 2,9·10-13 s alatt. Ebből arra következtethetünk, hogy a héjvastagság és a Compton-sugár aránya exponenciálisan változtatja meg a fermionok stabilitását, és elektron esetén az élettartam akár az univerzum korát is elérheti.
-
12. A Z bozon színre lépése
A gyenge kölcsönhatás olyankor is megfigyelhető, amikor nem történik részecskeátalakulás. Buborékkamrában vizsgált elektronoknál azt tapasztalták, ha jelentős neutrínó fluxus halad át a kamrán, egyes elektronok mozgása hirtelen megváltozik (Carlo Rubbia, Simon van der Meer, Nobel díj: 1984). Ezt úgy lehetett értelmezni, hogy az elektron lökést kaphat a neutrínóktól, amit viszont csak egy új kölcsönhatás idézhet elő, hiszen gammasugarak nem voltak jelen. Itt arra kell gondolni, hogyan tudja az egyik test meglökni a másikat, amikor nekiütközik? Számunkra ez természetesnek tűnik, pedig ez a lökés nem jöhetne létre elektromágneses kölcsönhatás nélkül! A neutrínó például nem rendelkezik elektromos töltéssel, ezért bár óriási számban áramlanak a Napból, hatásukat nem vesszük észre, gyakorlatilag veszteség nélkül haladnak át az egész Földgolyón! A neutrínó sugárzás során meglökött elektronok töltése változatlan marad, ami töltéssel nem rendelkező bozon jelenlétére utal, ez a részecske zéró töltése miatt a Z bozon nevet kapta. A szakirodalom a folyamatot rugalmas neutrínó szórásnak nevezi, amely az jelzi, hogy a folyamatban nem alakul át a meglökött elektron más részecskévé.
A fénysebességű forgásmodell úgy értelmezi a Z bozont, mint két ellentétes kiralitású spirálmozgás szuperpozícióját. A W bozonhoz hasonlóan a semleges Z bozon tömegénél fogva impulzussal rendelkezik, és ezt ütközéskor átadhatja elektronoknak a gyenge kölcsönhatás révén.
A kísérletek során meghatározták a Z bozon tömegét, amit 91,2 GeV/c2 nagyságúnak találták, ez meghaladja még a W bozon tömegét is. Ez úgy értelmezhető, hogy a semleges neutrínók héjvastagsága valamivel kisebb a töltéssel rendelkező fermionokhoz képest. Vagyis a tér minimális görbületi sugara lecsökken semleges töltésű részecskék formálódása esetén:
Rmin = 2,165·10-18 m
-
13. Higgs bozon és a fénysebességű forgások
Higgs koncepciója is új szerepet ad a térnek, amelynek szimmetriatörésére vezeti vissza az ősi részecske színrelépését, amelynek bomlástermékei hozzák létre a fermionok és bozonok tömegét. Ezt a részecskét nevezzük ma Higgs bozonnak, és az a mező, amely ezt megteremti a Higgs mező. Ennek a részecskének nincs töltése és spinje sem, emiatt fénysebességű forgások sem tartoznak hozzá. Viszont ez a részecske teremti meg az előfeltételét, hogy ebből a szimmetriatörésből kialakuljanak a fénysebességű forgások, azaz a fermionok és a spinnel rendelkező kölcsönhatási bozonok. Az LHC kísérletek egyértelműen bizonyították, hogy létezik egy 127 GeV energiájú részecske, ami megfelel azoknak a tulajdonságoknak, amit a Higgs bozonnak teljesíteni kell. Tömege elég nagy ahhoz, hogy kisarjadjanak belőle a W és a Z bozonok, majd ezek bomlásaiból az elemi részecskék teljes világa. Mivel a Higgs bozont nem fénysebességű forgások alkotják meg, így nem vonatkozik rá a szabály, amely behatárolja a maximális részecske tömeget. A Higgs bozon létezését alátámasztó kísérletek így egyúttal a fénysebességű forgás koncepciójának is bizonyítékai.
-
15. Lépés a kölcsönhatások egyesített mezőelmélete felé
A mezőelméletek, tehát a kvantumelektrodinamika és annak gyenge kölcsönhatással egyesített változata az elektrogyenge kölcsönhatás elmélete, valamint a kvantumkromodinamika (ez írja le az erős kölcsönhatást), egységes keretek között tárgyalja a három kölcsönhatást: az elektromágneses, a gyenge és az erős kölcsönhatást. Viszont hosszú ideje tartó elméleti erőfeszítések ellenére sem sikerült a képbe beilleszteni a gravitációt. Ennek a feloldására tesz kísérletet a fénysebességű forgások koncepciója. A kölcsönhatások véges sebességgel terjednek, ez a fénysebesség, amelynek magyarázata fénysebességű közvetítő folyamatokat igényel. A gravitáció kivételével a közvetítést az S = 1 spinű bozonok végzik el, melyeket a fénysebességű modell egytengelyű forgásokként ír le. Ebben a fénysebesség a kulcsszereplő a kvantum létrehozásával. Az első részben leírtak szerint a gravitációnak is van közvetítője, a kéttengelyű és a távolsággal csökkenő frekvenciájú S = 0 spinű forgáskombináció, amelyhez nem tartozik kvantum. Ha kiterjesztjük a részecskefogalmat, ezt a mozgást is felfoghatjuk részecskének, amely csak virtuálisan létezik, és szerepe, hogy felépítse a tér gravitációs görbületi struktúráját.
A fénysebességű forgásmodell csak egy lépést tesz a végső egységesített elmélet megalkotása felé. A megoldandó feladatot az okozza, hogy a Standard Modell valójában nem több, mint egy adatgyűjtemény, ugyanis hiányzik belőle az elméleti keret, amelyből le tudnánk vezetni a mért adatok hosszú sorát. Példaként vegyük az elektron, a müon és a tau részecskék tömegarányát. Olyan elméletre lenne szükség, mint ami az atomokban meghatározza az egyes elektronpályák diszkrét energiáját. Ennek alapja a fotonok szabályozó szerepe, amely kijelöli az elérhető energiaszinteket, amit az elektronpályák impulzusnyomatékához kapcsol. Ennek mintájára képzelhetjük el, hogy a fénysebességű kettős forgások közül az elektron képviseli az alapállapotot, a müon és tau részecske pedig gerjesztett állapotnak felel meg, ahol a gerjesztési frekvenciákat a gyenge-kölcsönhatás határozza meg a W bozon által. Ez persze bonyolultabb folyamat, mint ami meghatározza az elektronok energiáját az atomokban, mert a bozon mellett egy másik részecske is szerepet játszik a gyenge kölcsönhatásban, mégpedig a neutrínó. Bár a fénysebességű forgásokra alapozott modellel sikerült nagyságrendi magyarázatot adni a részecskék tömegarányára, de továbbra sincs meg az egzakt elmélet, amely pontos értékeket szolgáltatna. Ennek megtalálása még a jövő feladata.
ÖSSZEFOGLALÁS
A fénysebességű forgás mint szemléleti módszer
A fénysebességű forgás a fizika olyan szemléleti módszere, amely maximálisan támaszkodik a modern fizika eredményeire, a speciális és általános relativitáselméletre, a kvantummechanikai mezőelméletekre és a részecskefizikára. Segít megérteni a sokszor nehéz matematikai eszközökkel dolgozó elméleteket, szemléletessé téve azokat. Új megvilágításba helyez fizikai fogalmakat, mindenekelőtt a fizikai teret, amit az anyagi világ aktív szereplőjének tekint, amely önmozgásaival hozza létre a részecskéket. A tér új szerepére épül Higgs koncepciója is, amikor a részecskék és a tömeg keletkezését a tér szimmetriatörésére vezeti vissza, amely maga nem fénysebességű forgás, hanem annak előfeltétele. A fénysebességű forgás új értelmezést ad a tömeg, az elektromos és színtöltés eredetére, és kapcsolatot teremt a fizika különböző területei között. Néhány esetben egyszerűbb számítási módszert kínál fizikai állandók meghatározására, azáltal, hogy szerves kapcsolatot épít ki a kvantummechanikai és a klasszikus fizikai látásmód között. A koncepció segítségével ki lehet küszöbölni néhány paradoxont is, amibe a modern fizika beleütközött.
Mindazonáltal a fénysebességű forgások koncepciója nem teszi fölöslegessé a mezőelméleti és a részecskefizikai módszerek alkalmazását, viszont segíti azok befogadását, amikor új megvilágításba helyezi az alapfogalmakat, és kapcsolatot épít ki a józanész világával. A fénysebességű forgások koncepciója segít abban is, hogy egy lépéssel közelebb juthassunk a négy alapvető fizikai erő közös elméletének megtalálásához. Összeköti a gravitációt és az elektromágnesességet azáltal, hogy mindkettőt a fermionból kiáradó virtuális forgásokra vezeti vissza, viszont amíg a gravitációt közvetítő kettős forgás nem fénysebességű mozgás, addig a fotonoknál az egytengelyű forgások fénysebességgel mennek végbe. A gyenge kölcsönhatást az köti össze az elektromágnesességgel, hogy mindkettő egy forgás és egy haladó mozgás kombinációja, csak az előbbinél a haladási irány merőleges, az utóbbinál párhuzamosa forgástengellyel. Az erős kölcsönhatás annyiban hasonlít az elektromágnesességhez, hogy a másodlagos mozgás iránya párhuzamos a forgástengellyel, de az erős kölcsönhatásnál ez a mozgás nem előrehaladás, hanem oszcilláció. Az erős gravitáció fénysebességű kettős forgásai alkotják meg a fermionokat a térben, azáltal, hogy extrém görbületet hoznak létre, amelynek potenciális energiája kiegyenlíti a centrifugális erőt. Az így képződő fermionok kerülnek egymással kölcsönhatásba a gravitációs és elektromágneses erők, valamint az erős kölcsönhatás révén. Végül a gyenge kölcsönhatás gondoskodik arról, hogy a különböző fermionok átalakulhassanak egymásba, és megszabja a végső határt a tér maximális görbületére, azaz a részecskék maximális tömegére.
Az einsteini gondolat szerint a gravitáció ekvivalens a gyorsulással együtt járó tehetetlenségi erővel. Ezt a gondolatot viszi tovább a fénysebességű forgások koncepciója, amikor a többi kölcsönhatást is kapcsolatba hozza a forgó rendszerek tehetetlenségi erőivel, jelesül a Coriolis, a centrifugális és az Euler-erővel. A kiterjesztett ekvivalencia elv révén közelebb kerülhetünk a régóta keresett célhoz, hogy megtaláljuk a kölcsönhatások egyesített mezőelméletét.
A blog további írásai elérhetők: „Paradigmaváltás a fizikában”
Az einsteini gondolat szerint a gravitáció ekvivalens a gyorsulással együtt járó tehetetlenségi erővel. Ezt a gondolatot viszi tovább a fénysebességű forgások koncepciója, amikor a többi kölcsönhatást is kapcsolatba hozza a forgó rendszerek tehetetlenségi erőivel, jelesül a Coriolis, a centrifugális és az Euler-erővel. A kiterjesztett ekvivalencia elv révén közelebb kerülhetünk a régóta keresett célhoz, hogy megtaláljuk a kölcsönhatások egyesített mezőelméletét.
A blog további írásai elérhetők: „Paradigmaváltás a fizikában”



