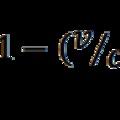A részecskék fénysebességű forgásmodellje

Közelebb juthatunk a kvarkok és gluonok különleges tulajdonságainak megértéséhez, ha valamilyen geometriai alakzathoz tudjuk kötni mozgásukat és szerkezetüket. A kvarkok fermion típusú elemi részecskék és spinjük S = ½. Evvel szemben a kölcsönhatásokat közvetítő elemi bozonok spinje S = 1, ami egyaránt vonatkozik az elektromágneses kölcsönhatást közvetítő fotonokra, a gyenge kölcsönhatás W és Z bozonjaira, valamint az erős kölcsönhatáshoz rendelt gluonokra. A fénysebességű forgás koncepciója szerint a fermionok és bozonok tulajdonságai a részecskéket alkotó forgások szimmetriájára vezethető vissza. Az S = 1 spinhez a tér lokális egytengelyű forgása tartozik, szemben az S = ½ spinű fermionokkal, ahol két egymásra merőleges tengely körül történik a forgás. Mivel a c fénysebességet nem lépheti át a forgás kerületi sebessége, így térben véges alakzatok alakulnak ki, egytengelyű forgásnál a kör sugara, kéttengelyű esetben a gömb sugara lesz véges az r = c/ω szabály szerint, ahol a forgás ω körfrekvenciája határozza meg az energiát: E = ħ ω (itt ħ= h/2p a redukált Planck-állandó). Az energiából származtathatjuk a tömeget is: m = ħ·ω/c². (Fermionoknál ez valódi tömeg, fotonoknál a nyugalmi tömeg nulla, itt effektív, vagy mozgási tömegről beszélhetünk). Szintén eljuthatunk a foton frekvencia független impulzusnyomatékához is az m·r·c = ħ összefüggésből, ahol figyelembe vettük, hogy a kerületi sebesség c és a mozgás merőleges a sugárra. Fermionoknál az impulzusnyomaték feleződik a fotonhoz képest, mert két egymásra merőleges forgás – azaz gömbforgás – hozza létre ezeket a részecskéket. Ez a forgás a gömb 4r²π felületét futja be, vagy másképp fogalmazva, a forgás kétszer járja be a 2rπ kerületet. Ez a felfogás a matematikai csoportelméletben alkalmazott meglepőnek látszó definíciót is érthetővé teszi, ahol az S = ½ spinű rendszerekben nem a 2p szögű teljes forgás az identitás elem, hanem annak duplája, azaz 4π. A forgás szögtartományának duplázódása viszont felezi az ω körfrekvenciát, ami együtt jár az impulzusnyomaték feleződésével is.

Virtuális folyamatok megjelenése a kvantummechanikában

A részecskéket alkotó lokális forgásokat azonban nem tudjuk megfigyelni, mert ezek a forgások nem bocsátanak ki fotonokat, azaz nem „láthatók”. Hasonló a helyzet a mikrovilág más területein is, ennek példája a kvantumelektrodinamika, amely nem detektálható folyamatokkal értelmezi az elektromágneses kölcsönhatást, amikor is megfigyelhetetlen fotonokról – úgynevezett virtuális fotonokról – értekezik. Tulajdonképpen a kvantummechanika stacionárius elektronpályája is virtuális, hiszen ezeken a pályákon a keringő elektron töltése nem bocsát ki, és nem is nyel el fotonokat. Detektálni csak a pályák közötti ugrásokat lehet. Ennek a felfogásnak a szellemében nevezhetjük a részecskéket alkotó elemi forgásokat is virtuálisnak. Ebből az is adódik, hogy a részecskék sajátforgásait a kvantummechanika módszereivel kell kezelni, amely valószínűségi eloszlásokkal és szimmetriákkal operál. Fermionok esetén ez egyfelől gömbszimmetrikus valószínűségi eloszlást, másfelől királis szimmetriát jelent, ahol az utóbbit a két forgás egymáshoz viszonyított polarizációs iránya határozza meg. A kiralitás lehet jobb kéz, vagy bal kéz szimmetriájú, amely megmondja, hogy anyagról (leptonoknál elektron), vagy antianyagról (leptonoknál pozitron) van-e szó, továbbá meghatározza az elektromos töltés előjelét is.

A kvantumelektrodinamika már továbblép azon a felfogáson, hogy nem történik fotonkibocsátás stacionárius állapotban, amikor feltételezi, hogy léteznek állandóan kibocsátott és elnyelt virtuális – tehát nem detektálható – fotonok. Ez a folyamat írja le a fermionok közötti elektromágneses erőhatásokat.

Az elektromágneses kölcsönhatás értelmezése Coriolis-erővel

A fénysebességű forgásmodell Einstein felfogását követi, aki a gravitációt a gyorsulással szembeni tehetetlenségi erőre vezette vissza. Esetünkben az F = e²/r² Coulomb-erőhöz keresünk valamilyen tehetetlenségi erőt. Abból indulunk ki, hogy a forgó rendszerekben mozgó testekre hat a Coriolis-erő, melynek nagysága c sebességű mozgásoknál F = 2mωc lesz, ha a sebesség iránya merőleges a forgási tengelyre. Kettős forgásnál, ha az x tengely az elsődleges forgás, akkor az y tengely körüli forgás y irányban oszcilláló, ħc/r² amplitúdójú, Coriolis-erőt hoz létre, ahol az amplitúdó számításában figyelembe vettük, hogy a kettős forgások által létrehozott fermionok impulzusnyomatéka ħ/2. A Coriolis-erő indítja útjára, vagy fogadja be, a kölcsönhatást közvetítő virtuális fotonokat, amelynek hatásfokát a dimenziómentes α = 1/137 Sommerfeld-állandó adja meg. Ez határozza meg az elektromos töltés nagyságát is: e² = αħc.

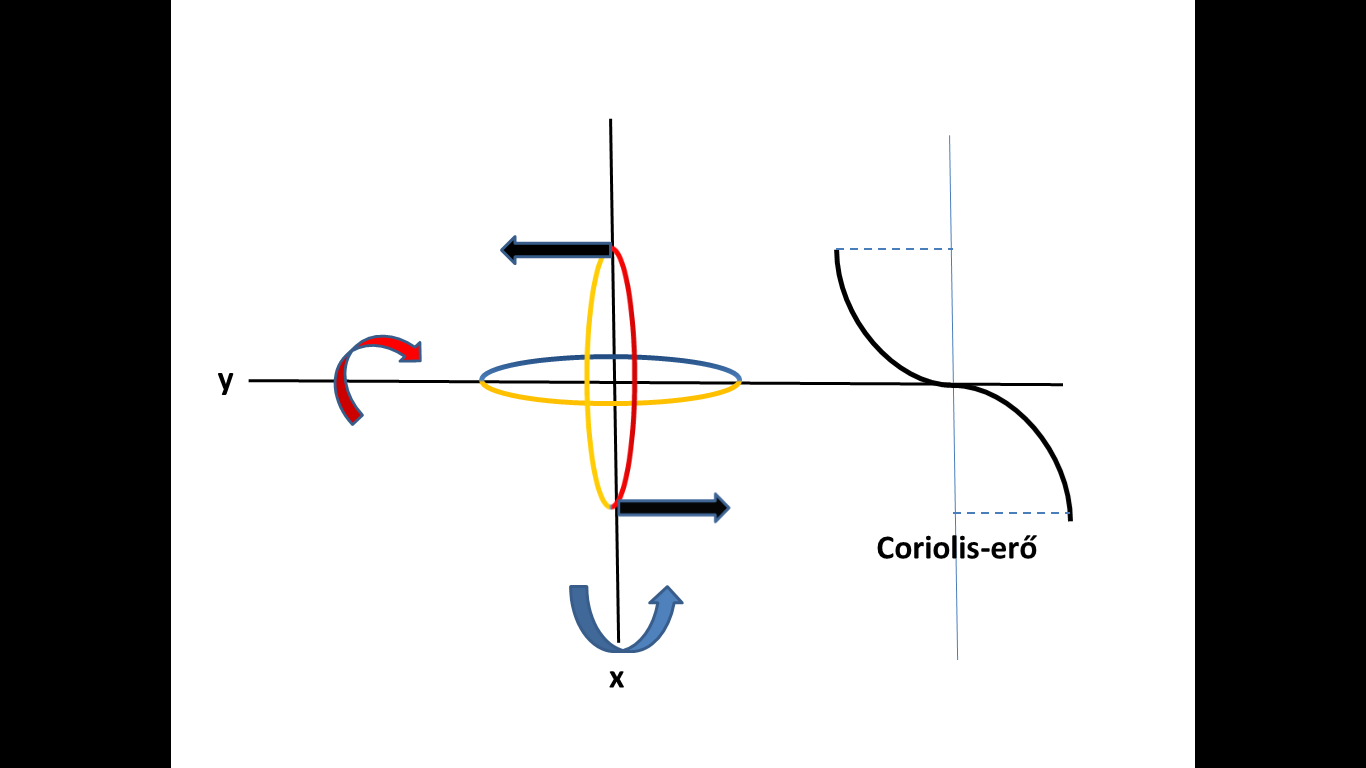
1. ábra. Kettős forgásokban fellépő oszcilláló Coriolis-erő (fekete nyíl mutatja az amplitúdót)

Kvarkok mozgásformái és a húrrezgések

Hogyan értelmezhetjük fénysebességű forgásokkal a kvarkok törttöltését, és két alaptípusának: up (röviden u) és down (d) létezését. Miért lépnek fel épp harmadok a töltésekben: ±2/3e és ±1/3e, és miért épp három kvark alkotja a barionokat? Arra könnyebb válaszolni, hogy a leptonoknál és kvarkoknál miért létezik három generáció: ez értelmezhető a fénysebességű forgások generációnként növekvő frekvenciájával. A Standard Modell szerint a második generációban charm (c) és strange (s), a harmadikban top(t) és bottom (b) tartozik ugyanabba a típusba, mint az up és down kvark.

A forgásmodell felépítéséhez analógiát nyújtanak a húr rezgései! A két végén rögzített húr alaprezgése a fél hullám, de létrejönnek felharmonikusak is: egész hullám, másfél hullám stb. Erre rímelnek a kvantummechanikában a molekulavibrációk, ahol a vegyértékrezgéseket az n = 0, 1, 2 … kvantumszám jellemzi. Az n = 0 típusú oszcilláció feleltethető meg a húr alaprezgésének, amit zérusponti rezgésnek is neveznek, mert még alapállapotban se áll le az összekapcsolt atomok mozgása, és ezáltal megnövekszik a molekula energiája is. Ez eltér a kifeszített húrtól, amelyik nyugalomban van, amíg nem pendítjük meg. Az alapállapotú vegyértékrezgés térbeli eloszlásának egy maximuma van és nincs csomópontja, ebben a húr fél hullámához hasonlít. A gerjesztett n =1 molekularezgés viszont már két maximummal és egy csomóponttal, az n = 2 pedig 3 maximummal és 2 csomóponttal rendelkezik, akárcsak a húrrezgés felharmonikusai. 

Oszcilláló forgások hármas szerkezete

Beszélhetünk-e hasonló gerjesztett állapotokról, ha nem oszcillációról, hanem forgásokról van szó? A rezgés és forgás kapcsolatba hozható, hiszen ha a forgómozgást az átmérőre vetítjük, akkor oszcillációkat kapunk. Azt kell tehát keresnünk, hogy milyen szerkezetű forgás vetülete felel meg az egyes n = 0, 1, 2 oszcillációknak?  Induljunk ki az egyszerű forgásból, amely folyamatosan körbeszalad! Itt a forgás vetületének közepén fellép egy maximum és nincs csomópont. De bontsuk fel a körbejárást részforgásokra (hurkokra), mégpedig oly módon, hogy a mozgás során csomópontok, illetve maximumhelyek alakuljanak ki! Ehhez az kell, hogy az első részforgás félúton lépjen át egy másodikba, ami úgy valósulhat meg, ha az új hurok forgásiránya fordítottja lesz az előzőnek. Például, ha az első részforgás iránya megegyezik az óramutató járásával – jelöljük ezt „+” szimbólummal – akkor a második hurok mozgása már szembe megy az óra járásirányával, amit a „– ” szimbólummal jelölhetünk. Ez viszont azt jelenti, hogy a második részforgás félfordulat megtétele után szembemegy az alapforgással (lásd 1. ábra). Ilyen kételemű „+–” felbontás ezért nem lehetséges. Ki kell tehát zárni a lehetőségek közül a két részforgásból álló és egy csomópontos összetett forgásokat. Viszont, ha a második részforgás átmegy egy harmadikba, akkor a forgáskombináció a félfordulat után egyirányú lesz az alapforgással. Ebből az elvből következik, hogy az összetett forgásban csak páratlan számú hurok lehet, melyek közül a legegyszerűbb a háromhurkos „+–+” felbontás, amelyben két csomópont és három maximumhely található. A csomópontokat tartalmazó forgás koncepciója tehát összhangban van a barion típusú részecskék hármas szerkezetével. (Lehetne még 5 hurkos összetett forgás is, de erre csak akkor lenne szükség, ha a részecskék Standard Modelljében lennének 5 részecskéből álló barionok is.) Leptonokhoz (elektron, pozitron, neutrínó) képest az a döntő különbség, hogy a kvarkoknál nem ekvivalens a két forgás, és ez az aszimmetria új típus kölcsönhatásokhoz vezet.

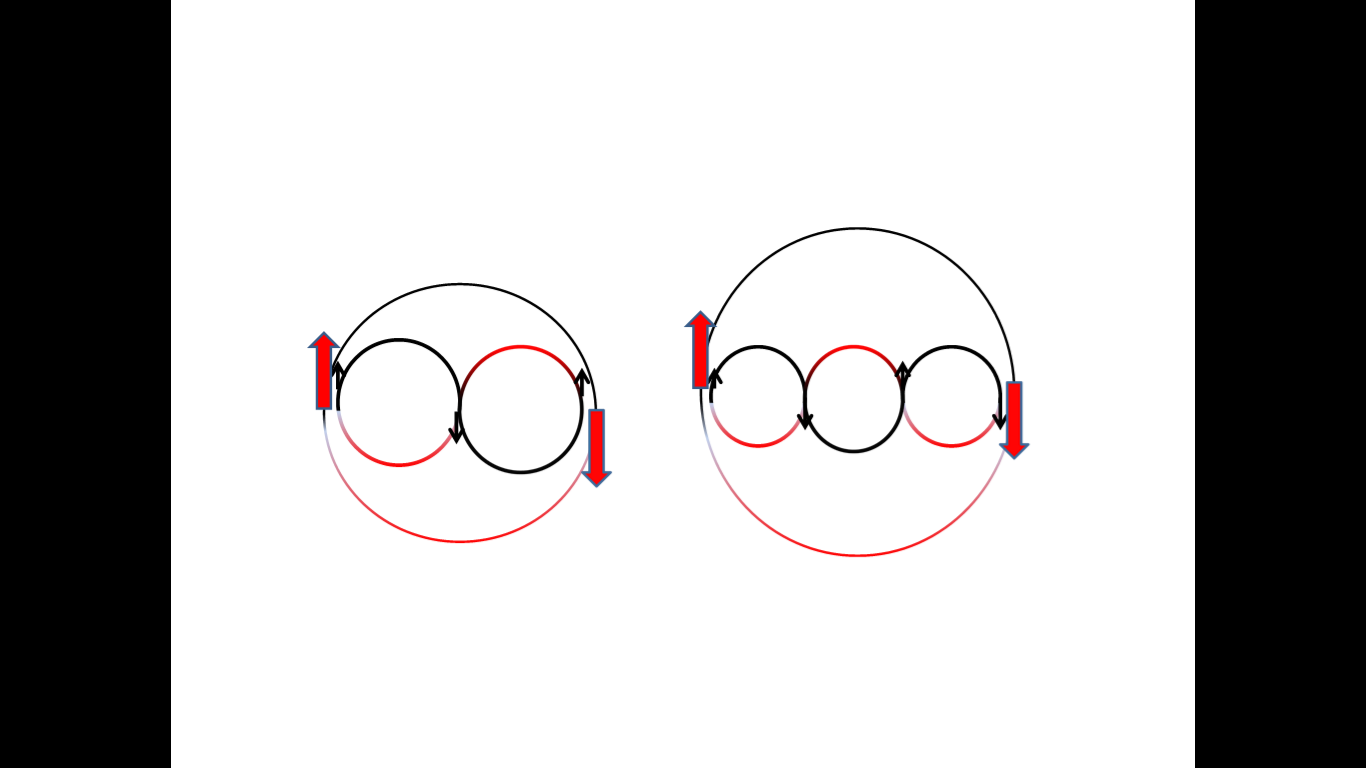
2.ábra. Balra: két hurokra bontott, jobbra: három hurokra bontott forgás körüljárási iránya az egyszerű forgáshoz képest

Miért rendelkeznek a kvarkok törttöltésekkel?

Térjünk most rá a törttöltés eredetére! Az S = ½ spinű fermionokat kettős forgások hozzák létre, melyben nevezzük az egyik forgást X-nek, a másikat Y-nak. Csak a második, azaz Y forgás legyen összetett. A kvarkok törttöltéséhez úgy juthatunk el, ha az Y forgás felbontásában szereplő egyes részforgások tengelye párhuzamos az X forgással (nincs Coriolis-erő), mások viszont merőlegesek X-re (van Coriolis-erő), az előbbi tengelyt x, az utóbbit y jelölje, Ez a választás nem változtatja meg az S = ½ spin értékét, ha az összetett pálya mozgásiránya végig merőleges a sugárra, hasonlóan az egyszerű körforgáshoz. Két lehetséges forgáskombinációt írhatunk fel: (xyx), iletve (yxy).  Az X egyszerű forgás és a felbontott Y forgás között akkor lép fel Coriolis-erő, ha a részforgás tengelye merőleges az egyszerű forgás x tengelyére, ennek megfelelően az (xyx) forgáskombináció esetén ±1/3e, míg (yxy) esetén ±2/3e töltés jöhet létre. A töltés előjelét viszont a körüljárási irány határozza meg, amit „+” és „–” indexekkel jelölhetünk, ily módon négy forgáskombinációhoz jutunk:  (x⁺y^–x⁺), (x^–y⁺x^–), (y⁺x^–y⁺) és (y^–x⁺y^–). Itt a két külső részforgás előjele a teljes Y forgás előjelével egyezik meg, ami lehet „+” és „–”, de evvel szemben a középső részforgás előjele fordított a teljes Y forgáshoz képest. A részecske-antirészecske kettősséget az X és Y forgásirányok egymáshoz viszonyított iránya, azaz a kiralitás határozza meg: a teljes Y⁺ és Y^– forgások közül az előbbit tekintsük olyan kiralitásúnak, amelyik anyagi részecskét hoz létre, míg az utóbbi forgás kiralitása antirészecskének felel meg. Ugyanezt úgy is megfogalmazhatjuk, hogy felcseréljük az X és Y forgások szerepét, amit YX típusnak nevezhetünk. Ekkor az Y forgás lesz az egyszerű, és az X forgás az összetett, és az XY-YX kombináció kvark-antikvark párt alkot. Mindkét esetben a felsorolt négy forgáskombinációhoz tartozó töltés –1/3e, +1/3e, +2/3e és –2/3e lesz. Az így megfogalmazott konvenció miatt a +2/3e töltésű (y⁺x^–y⁺) és a –1/3e töltésű (x⁺y^–x⁺) kombinációk felelnek meg a down és up kvarkoknak, míg a másik két kombináció reprezentálja az antikvarkokat.

.

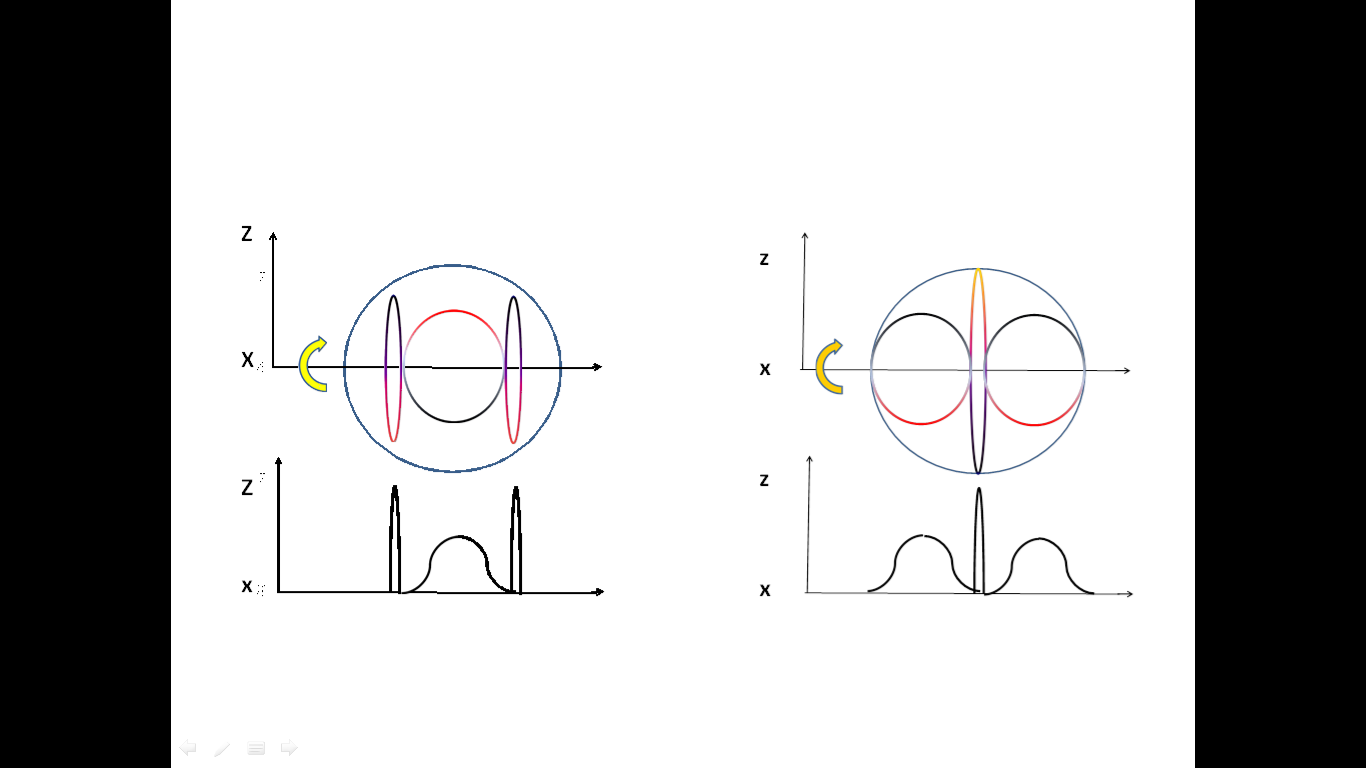
3. ábra. Balra xyx, jobbra yxy típusú oszcillációs forgások és vetületeik

Oszcillációk kötött rendszerekben

Kvarkokra javasolt mozgásformát oszcillációs forgásnak is nevezhetjük, mert az Y forgás három hurkának z-irányú kitérései oszcillációt alkotnak. Az oszcilláció megjelenése összhangban van a kvantummechanika már említett törvényével, miszerint minden kötött rendszer zérusponti rezgés végez, azaz még alapállapotban is van oszcilláció.

Az állítás meg is fordítható: csak akkor alakul ki oszcilláció két objektum kötött, ha valamilyen erőhatás összeköti őket. A kvarkokból felépülő barionokban és mezonokban az összetartó erőt az erős kölcsönhatás képviseli, ezért a bezártsági elv, mely szerint szabad kvark, azaz törttöltés megfigyelése nem lehetséges, összhangban van avval a felfogással, hogy a kvarkokat oszcillációs forgások alakítják ki. Úgy is fogalmazhatunk, hogy a törttöltésű kvark egy alacsonyabb szimmetriájú részállapot (mintázat) a magasabb szimmetriájú összetett struktúra (barion és mezon) belsejében, és a „mintázat” szerkezetét a részecskét egyben tartó erős kölcsönhatás határozza meg. Ez az erő alakítja ki az oszcillációs forgásokat, melyben a pályamozgás során megváltozik a forgástengelyek iránya is.

Mi a kvarkok színtöltésének eredete?

A kvarkelmélet meghatározza, hogy a mezonok és barionok szerkezete milyen kvarkkombinációkból épül fel. Vizsgáljuk meg, hogy a felépítési elv hogyan teljesül a kéttengelyű forgások modelljében. Nézzük először a barionokat, amelyek a Standard Modell szerint vagy három kvarkból, vagy három antikvarkból épülnek fel. A barionok spinje lehet ½, vagy 3/2, ez a lehetőség a spinek szokásos összeadási szabályából következik. Mivel a barionokban vagy csak kvarkok, vagy csak antikvarkok vannak, és az előbbi töltése 2/3e, vagy       –1/3e, az utóbbié 1/3e, vagy –2/3e, így belátható, hogy csak az elemi töltés egész számú többszöröse jöhet létre (nulla, ±e és ±2e), amikor három részecske kapcsolódik össze. A kvarkoknak a töltésen és spinen kívül van azonban egy további szabadsági fokuk is: a színtöltés. Ez három különböző értéket (színt) vehet fel, ugyanakkor a belőlük felépülő barionok szín semlegesek, azaz a bariont felépítő három kvark, vagy antikvark különböző színű, amelynek eredője „fehér” lesz. Eddig XY típusú kvarkokról beszéltünk, de ugyanilyen joggal választhatunk YZ és ZX forgásokat is, ahol mindig az első az egyszerű, a második az oszcillációs forgás. Ezt a három forgáskombinációt rendelhetjük a kvarkok három színéhez, viszont a barionok színsemlegessége („fehér színe”) azt követeli meg, hogy a három kvarkban, vagy antikvarkban az XY, YZ és ZX, illetve YX, ZY és XZ forgástípusok egyenlő súllyal szerepeljenek. Ez gömbszimmetrikus (izotrop szerkezetű) barionok esetén teljesül.

A barionok összetételének még eleget kell tenni a Pauli-elvnek is, amely megköveteli, hogy kötött kvantumállapotban ne forduljon elő két olyan fermion, melyek minden kvantumszáma egyezik. Ez azt jelenti, hogy nem lehet két kvarknak mind a töltése, mind a spin vetülete (+½ és –½), mind a szín-kvantumszáma és még generációs indexe is azonos. Három azonos kvarkból álló barion azonban létrejöhet, például az (uuu), vagy (ddd) konfigurációk, éppen a kvarkok különböző színére vonatkozó szabály miatt. Megjegyezzük még, hogy az atommagokat felépítő két nukleon, a proton és a neutron szerkezete: (uud), illetve (udd).

A hadronok másik csoportját a mezonok alkotják, amelyek egy kvarkból és egy antikvarkból épülnek fel. Töltésük szintén csak az elemi töltés égésszámú többszöröse lehet, azaz 0 vagy ±e. A kvarkokra felírt töltéskonvenció itt is kizárja a törttöltésű részecskék létezését. A spin lehet 0, vagy 1, megfelelően annak, hogy bozonokról van szó. A mezonoknak sincs színük, amit az biztosít, hogy az antikvarkok színe a kvarkok színének komplementere. Ez megkívánja, hogy az XY és YX kombinációk színe egymás komplementere legyen.

Hogyan forrasztják össze a kvarkokat a gluonok?

A Standard Modell 8 független gluonnal értelmezi a kvarkokat összekötő erős kölcsönhatást. A gluon is bozon, és spinje S = 1. A fénysebességű forgásmodell szerint valamilyen tengely körüli mozgás alkotja a bozonokat, amely mozgás csatlakozik egy forgástengellyel párhuzamos másik mozgáshoz. A párhuzamosság abból következik, hogy a gluonoknak a fotonokhoz hasonlóan nincs elektromos töltésük, rendelkeznek viszont színtöltéssel. De milyen lehet ez a másodlagos mozgás?

Nézzük először, hogyan is közvetíti az erőhatást a foton két töltött részecske között a kvantumelektrodinamika szerint? A töltött részecskék virtuális fotonokat bocsátanak ki (emisszió) és nyelnek el (abszorpció), melynek polaritását a részecske királis szimmetriája határozza meg. Ez a folyamat véletlenszerű fluktuációkat hoz létre a részecske pozíciójában (vákuum fluktuáció), de nem mozdítja el. Ha viszont a virtuális foton egy másik töltött részecskéhez eljut és elnyelődik, akkor vagy meglöki azt, (ha a két töltés előjele azonos), vagy a két részecskét egymás felé húzza (ha ellentétes a töltések előjele). Így jön létre taszítás, vagy vonzás. A virtuális gluonok hatása ettől annyiban különbözik, hogy a gluon alkalmazkodik a kvarkok színéhez, és kizárólag vonzást hoz létre függetlenül a kiralitástól. A gluon kiralitás függetlensége abban nyilvánul meg, hogy nincs elektromos töltése. Két kvark összekapcsolásához viszont két szín tartozik: az egyik a kibocsátó kvark színe, a másik az abszorbeáló kvark színének komplementere (az abszorpció a szín komplementerét igényli). A kvarkok színét a kettős forgás aszimmetriájára vezethetjük vissza. Például az XY oszcillációs kettős forgást „y⁺” színűnek nevezhetjük, mert ebben az irányban oszcillál a Coriolis-erő, és pozitív indexet használunk, mert kvarkokról van szó. Evvel szemben az YX antikvarkhoz az  „x^–” komplementer színt rendeljük hozzá. A negatív index annak felel meg, hogy az oszcillációs fázis fordított. Ezt az elvet követve vezethetjük be a YZ és ZX kvarkok esetén az „z⁺” és „x⁺” színeket, míg a ZY és XZ antikvarkoknál az „y ^–” és „z ^–” komplementer színeket. Összesen tehát három alapszínről és  azok komplementer színeiről beszélhetünk.

Kvarkok esetén az oszcilláló forgás és az egyszerű forgás között fellépő Coriolis-erő bocsátja ki a gluonokat, de ez sokkal erősebb az elektromos erőnél, minthogy a kvarkok közvetlenül érintkeznek a barionokban.. Emiatt az erős kölcsönhatás mértékét a ħc szorzat csillapítás nélkül adja meg, azaz mintegy 137-szer lesz erősebb az elektromágneses kölcsönhatásnál. A kölcsönhatás erőssége nem változik a barion mérettartományán belül, viszont azon kívül, ahol már nincs kontaktus, gyorsan megszűnik.

Az elmondottak értelmében a gluon tehát irányváltoztató (színváltoztató) kölcsönhatás, amely az egyik irányú oszcillációt átviszi egy másik irányba, és evvel járul hozzá, hogy a magasabb szimmetriájú barionokon belül létrejöjjenek alacsonyabb szimmetriájú „mintázatok”, azaz kvarkok. A gluon így szerves tartozéka a két alapvető kvarkkonfigurációnak, a háromelemű barionoknak és a kételemű mezonoknak. Sem kvarkokat, sem gluonokat nem észlelhetünk szabadon, ezek a részecskék csak együtt létezhetnek az összetett részecskéken belül. Ez nyilvánul meg abban is, hogy nem tudunk valódi tömeget rendelni az egyes kvarkokhoz, csak renormált tömegekről beszélhetünk, hiszen a részecskék saját energiáját a kvarkok és gluonok együttesen alakítják ki.

A barionok három különböző színű kvarkból, vagy antikvarkból épülnek fel, ezért (x⁺y^–), (x⁺z^–), (y⁺x^–), (y⁺z^–), (z⁺x^–), (z⁺y^–) színváltoztató gluonok játszanak szerepet a kölcsönhatásban. A mezonokban azonban a színsemlegességet iránytartó (színtartó) gluonok hozzák létre, melyekben nem változik meg az oszcillációs irány, tehát a szín-kvantumszám. Jelöljük a színtartó gluonokat az (x⁺x^–), (y⁺y^–) és (z⁺z^–) szimbólumokkal. A negatív index mutatja, hogy a komplementer színek oszcillációs fázisa ellentétes a színekhez képest

Gluonok osztályozása a Standard Modellben

A kilenc gluon 3*3-as mátrixba rendezhető:

(x⁺x^–)   (x⁺y^–)   (x⁺z^–)

(y⁺x^–)   (y⁺y^–)   (y⁺z^–)

(z⁺x^–)   (z⁺y^–)    (z⁺z^–)

Összességében gömbszimmetrikus potenciáltér jellemzi az erős kölcsönhatást. Ennek megfelelően a háromdimenziós mátrix felbontható a forgáscsoport egy, három és öt dimenziós ábrázolásaira, hasonlóan az L = 0, L =1 és L =2 gömbfüggvényekhez. Az L = 0 gluon kombináció szingulett állapotnak felel meg, amelynek létezését a Standard Modell kizárja, emiatt beszél az elmélet nyolc független gluonról. A háromdimenziós L = 1 függvénytér szerepe a mezonokat összetartó erő leírása, míg az L = 2 ötdimenziós függvénytér hozza létre a barionokban uralkodó izotrop potenciálteret.

Az atommagokat összetartó erő

Az atommagok felépítése további kérdést vet fel: milyen erő köti össze benne a nukleonokat (proton és neutron). Ez a kvarkokat összekötő erős kölcsönhatás másodlagos következménye, amit a kvantummechanika kicserélődési erőnek nevez. Ez akkor jön létre, ha két összetett részecske, esetünkben a nukleonok, egymás között felcserélik az „alkatrészeiket”, azaz a kvarkok átjárhatnak a nukleonok között. A kicserélődési kölcsönhatás visszavezethető a fermionokra érvényes Pauli-elvre, hasonlóan ahhoz, ahogy az elektronok összekötik a molekulák atomjait. A kvarkok átjárása nukleonok közvetlen érintkezésekor valósul meg, magyarázva, hogy miért olyan rövidtávú a nukleonokat összekötő vonzó erő.

Pillanatkép az elemi részecskék belsejéből

Végül is, milyen képet alkossunk a gluonok és kvarkok világáról?  Képzeljük el úgy a hadront, mint egy kettősforgás által alkotott gömböt. Ebből az oszcilláló Coriolis-erő csavarmozgást végző fotonokat küld ki a külső térbe, amelyek összekötő rugóként lökik el, vagy húzzák maguk felé a töltött részecskéket. Ennek a gömbnek a felületén – arra merőlegesen – oszcillációk alakulnak ki, amelyek létrehozzák a gluonok kettős színvilágát. Ezt felfoghatjuk úgy is, mint a felszín „fodrozódását”, amely összekapcsolódik a gömb belsejében kialakuló kvark „mintázatokkal”. De ne feledkezzünk meg a gyenge kölcsönhatásról sem! (Lásd: Látogatás az elemi részecskék szerelő műhelyében: gyenge kölcsönhatás). A fodrozatok és mintázatok átalakulhatnak, és az átalakulás „melléktermékeként” létrejönnek további forgáskombinációk is. Erre példa a neutron béta-bomlása, amikor egy d kvark átalakul u kvarkba egy W^– bozon közvetítésével, és közben egy elektron és egy neutrínó távozik. Az átalakítást végrehajtó részecskéket – a W és Z bozonokat – szintén egy tehetetlenségi erő hozza létre: ez az Euler-erő, amely a forgási frekvencia változásakor lép fel. A gyenge kölcsönhatás bozonjai változó frekvenciájú és növekvő sugarú spirálforgások a gömb belsejében, amelyek rezonanciába kerülve az egyes kvarkokkal hajtják végre az átalakítást.

A gravitáció kapcsolata a többi fizikai kölcsönhatással

Fizikai világképünket a gravitációs erő teszi teljessé (Lásd: Térgörbület és gravitáció forgó rendszerekben). A részecskék kettős forgása is kiszabadulhat a gömbök belsejéből az Euler-erő hatására, de a külső forgás kerületi sebessége már lassul a távolsággal, és messze elmarad a fénysebességtől. Ezek a forgások sem láthatók, azaz virtuálisak, de létrehozzák a tér görbületét a fermionok körüli térben, és hatalmas számú részecske összefogásaként megalkotják a gravitációs erőmezőt.

A virtuális külső forgásokat is a kvantummechanika módszerével jellemezhetjük, megadva az állapotfüggvényt, amely leírja a kettősforgások frekvenciájának távolságfüggését, és valószínűségeket adhat meg a lehetséges pályafüggvényekre. Ezek a pályák megfelelnek klasszikusan a Kepler-Newton törvénynek, de az általános relativitáselmélet egyenletéből is származtathatók. Amikor egy bolygó, vagy egy égitest, kering központi csillagja körül, a lehetséges forgási pályák egyike kerül kiválasztásra, hasonlóan ahhoz, amikor az állapotfüggvény által megadott több lehetőség közül a mérés kiválaszt egyet.

A gravitációs keringés nem érheti el a fénysebességet, ezért kvantum sem tartozik hozzá, szemben a másik három kölcsönhatással, amelyet virtuális bozonok közvetítenek. Emiatt a négy alapvető fizikai erőt nem lehet a kvantumelv alapján egyesíteni, ehhez egy másik elv szükséges, amit a kölcsönhatásokat közvetítő virtuális forgások koncepciója adhat meg. A virtuális kettős forgások is fénysebességgel terjednek a térben, érthetővé téve, hogy miért terjed a gravitációs hatás is c sebességgel Einstein általános relativitáselmélete szerint.

A blog további írásait lásd: Paradigmaváltás a fizikában