Bevezetés

Einstein a gravitációt, az egyenletesen gyorsuló rendszerek tehetetlenségi erejével hozta kapcsolatba. Korábbi bejegyzésekben ( „Screw model for quantum electrodynamics” illetve „A részecske fizika nyitott kérdései „ ) kimutattuk, hogy a gravitáció értelmezhető forgó rendszerek segítségével is, mint a forgások révén létrehozott térgörbület centripetális ereje. Az elgondolást fénysebességű forgásokra kiterjesztve bevezettük a részecskék sajátforgását stabilizáló erős gravitáció fogalmát. Ebben a bejegyzésben először összefoglaljuk a gondolatmenet alapjait, majd utalunk rá, hogyan kapcsolódik az elképzelés Higgs spontán szimmetriatörési koncepciójához, kitérünk kozmológiai kérdésekre és a legkisebb hatás elvére is. 

Térgörbület és gravitáció forgó rendszerekben

 A Kepler-féle bolygómozgások törvényéből indulunk ki feltételezve, hogy a Nap a körül a bolygók „együtt úsznak” a tér pontjaival. Az ω körfrekvenciával és a centrumtól R távolságban forgó pont kerületi sebessége u = ω.R,  amely a kerület hosszát a Lorentz-kontrakció miatt lerövidíti r/R = (1 – ω²R²/c²)^1/2 mértékben  Mivel a rövidülés csak a kerületet érinti, míg a mozgásra merőleges R sugár hossza nem változik, így az r/R arány egyúttal a tér görbületét is jellemzi, amit a következő összefüggéssel adunk meg:

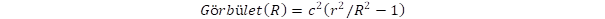
Itt a görbületi függvényt úgy választottuk meg, hogy a tömeggel szorozva megadja a gravitációs potenciális energiát, azaz gravitációs potenciálnak tekinthető. A negatív előjel annak felel meg, hogy a görbület vonzást hoz létre. A Lorentz-kontrakció figyelembe vételével a görbület:

Görbület(R) = –ω²R²

Helyettesítjük be a Kepler által megállapított összefüggést az ω körfrekvencia és az R átlagos távolság között:  ω²R³ = γ.M, ahol M a Nap tömege γ a gravitációs állandó:

Görbület(R) = – γ.M/R

A görbületet szorozva a Nap körül keringő bolygó m tömegével kapjuk a bolygó potenciális energiáját, majd ebből gradiens képzéssel eljutunk a Newton által megállapított gravitációs törvényhez:

F_gr = – γ.M.m/R² 

A Kepler-törvény miatt az u = ω.R kerületi sebesség az R távolsággal csökken, ezért a kerületi sebesség nagy R értékeknél is kisebb lesz a fénysebességnél. Viszont a fénysebességű forgásokon alapuló modellben, ahol az ω körfrekvenciát rendeljük a részecskéhez, van az R sugárnak egy felső határa, ami az u = ω.R ≤ c  szabály miatt nem lehet nagyobb, mint  R_c = c/ω. A modell sarkalatos pontja, hogy a fénysebességű és ezért R_c sugarú forgás hozza létre a tömeget a határértékben nullatömegű térből. Ez a tömeg viszont kizárólag az R_c sugarú körön illetve gömbfelületen jelenik meg, ahol a tömegnövekedési faktor végtelenhez tart, míg az R < R_c tartományban a véges tömegnövekedési faktor nem hozhat létre tömeget. Az R = R_c felületen koncentrálódó m tömegre hat a térgörbület centripetális ereje, amelynek potenciális energiája így V_sgr = –m.c² lesz. Ez épp kiegyenlíti a nyugalmi energiát,és amely a modell szerint nem más mint a forgáshoz tartozó kinetikus energia.

Fotonoknál a tömeg-energia ekvivalencia szabálya ℏ.ω = m.c² határozza meg a mozgási tömeget, ezt az összefüggést alkalmazzuk fermionok esetére is, ahol ω a kettős forgás frekvenciája, m pedig a nyugalmi tömegnek felel meg. Az r = c/ω sugár ekkor a ℏ/m.c  Compton-hullámhosszal egyezik meg, amit felhasználva azt kapjuk a –m.c² potenciális energiából, hogy:

V_sgr = –ℏ.c/r

A térgörbület centripetális ereje pedig:

F_sgr = . –ℏ.c/r²

Fénysebességű forgások és a Higgs-féle spontán szimmetriatörés 

Fénysebességű forgásnál a mozgás irányába eső dimenzió eltűnik, vagyis ekkor maximálisan elfajult térgeometria jön létre, ahol a görbület sok nagyságrenddel meghaladja a szokásos gravitációét, és ennek megfelelően a potenciális energia, illetve a hozzá tartozó erő is sokkal nagyobb. Ennek a ténynek adunk hangsúlyt, amikor a maximálisan elfajult térgörbülethez tartozó erőhatást megkülönböztetésül erős gravitációnak nevezzük, amit az „sgr” indexszel jelölünk. Kimondhatjuk tehát, hogy a térpontok fénysebességű forgása tömeggel rendelkező fizikai objektumot hoz létre a határértékben nullatömegű vákuumból. A téridőnek tehát kettős szereposztása van: a térpontok forgása hozza létre a tér görbületét, a görbület pedig stabilizálja a térpontok forgását. Az erős gravitáció esetén megfordul az Einstein által megfogalmazott logikai sorrend, mert nem a nyugalmi tömeg hozza létre a tér extrém görbületét, hanem a tér görbülete a tömeget. Az energiamérleg szempontjából ez úgy jelenik meg, hogy a térpontok fénysebességű forgásának m.c² kinetikus energiáját a tér görbületének –m.c² potenciális energiája ellensúlyozza. Ugyanez kifejezhető az erőkkel is: . a részecske forgó tömegét kiröpíteni akaró centrifugális erőt visszatartja  az erős gravitáció centripetális ereje. A teljes energia illetve erő, amelyik a téridő két különböző megjelenési formájának összegét fejezi ki, tehát zérus, és ez lehetővé teszi a részecskék spontán képződését a téridőből, ha létezik egy kezdő hatás, ami értelmezhető Higgs spontán szimmetriatörési koncepciója alapján, hiszen a tér torzulása miatt megszűnik a transzlációs szimmetria. Ily módon az erős gravitáció koncepciójában Higgs elképzelése a szimmetriatörésről konkrét formát ölt.

Miért van az anyag túlsúlyban az antianyaggal szemben?

Külső energiára tehát nincs szükség a részecske képződéséhez, szükség van viszont egy kezdő lökésre a két ellentétesen forgó perdület (spin) létrehozásához. Ez a folyamat többnyire két azonos nyugalmi tömegű részecske (például elektron-pozitron, vagy proton- antiproton) keletkezésével jár együtt, de nem zárhatjuk ki, hogy van olyan folyamat is, amikor aszimmetrikus párkeltés során egy elektron és egy proton (tehát nem pozitron!) jön léte. Ilyen folyamatot még nem mutatott ki a részecskefizika, de esetleges megfigyelése alátámasztaná az ismertetett fizikai elképzeléseket. Ez egyúttal magyarázatot adhatna a kozmológia egyik megoldatlan rejtélyére is, hogy miért uralkodik Univerzumunkban az anyag az antianyag felett. Ha minden párképződési folyamatban pontosan megegyezik a részecskék és anti-részecskék tömege, akkor ezek teljesen megsemmisítenék egymást az ütközések során, és így a statisztikai véletlen nem játszhatna szerepet. Ugyanakkor aszimmetrikus párképződések során csak valószínűségi egyezés áll fent az elektron-proton, és a pozitron-antiproton párok képződésénél, és így a statisztikai véletlen már eltérítheti egymástól a két folyamatot, ami utat nyithat az anyag dominanciájához az antianyaggal szemben. 

 A részecske világ és a görbült tér

A téridő két arculata közül csak a részecskevilág jelenik meg szokásos fizikai világképünkben, és ennek leírására szorítkoznak a relativisztikus mozgásegyenletek is. Ez a tárgyalásmód mindaddig kielégítő, amíg nem lép fel olyan erőhatás, amelyik összeköti a részecskéket és annak hátterét adó görbült téridőt. Létezik azonban olyan fizikai folyamat is, erre példa a neutronok béta bomlása, amikor a gyenge kölcsönhatás összeköti a téridő két megnyilvánulási formáját. Evvel a kérdéssel „Az elektro-gyenge kölcsönhatás és az elemi részecskék átalakulása” című bejegyzésben foglalkozunk.

Szemléltessük a látható részecskevilág és a görbült téridő láthatatlan háttérvilága közötti kapcsolatot egy hasonlattal. Képzeljük úgy el egy hajó mozgását a tengerben, hogy felveszünk egy speciális szemüveget, amelyik kiszűri a hajóról érkező fotonokat, de eljutnak hozzánk azok a fotonok, amelyek a tengerből származnak. Ekkor a tengerben csak egy hajó formájú és mozgó bemélyedést látunk. Milyen erőt kell a láthatatlan hajónak legyőzni a haladáshoz? A víz közegellenállását. Cseréljük ki a szemüveget olyanra, amelyik fordítva működik: csak a hajót látjuk, de nem látjuk a tengert. Ekkor úgy képzeljük, hogy a hajó az üres térben mozog. Valójában ez a helyzet akkor is, amikor a részecskék mozgását vizsgáljuk: nem veszünk tudomást arról, hogy a részecske sajátforgása egy erősen görbült térben történik, és úgy fogjuk fel a részecske tehetetlen tömegét, mint a részecskéhez tartozó tulajdonságot. Valójában azonban arról van szó, hogy amikor mozog a részecske, akkor evvel együtt rendeződik át a tér görbült struktúrája is és ehhez az átrendeződéshez le kell győzni a tér tehetetlenségét. Ebben az értelemben a test tehetetlen tömege voltaképp a görbült térnek a gyorsuló átrendeződéssel szembeni közegellenállása.

A fenti hajó hasonlat segít a részecske sajátforgását fenntartó erő szemléltetésében is. A hajó nem süllyed el a tengerben a víz felhajtó ereje miatt. Ezt a felhajtó erőt a hajó alatti bemélyedéshez, azaz görbülethez rendelhetjük az Arkhimédesz által megállapított törvény szerint. Az erős gravitáció ebben az értelemben a részecske által „kiszorított” tér összenyomó ereje. 

Tájkép a mikro-  és makro világról

A görbült tér ideáját először Einstein fogalmazta fel, amikor megalkotta a relativitás általános elméletét. A gravitációt előidéző tér görbülete – legalább is a mi környezetünkben – nagyon szelíd. Einstein elmélete makroszkopikus objektumokra vonatkozik, bolygók, csillagok, galaktikák gravitációs terét és mozgását írja le, ami alkalmazható feketelyukat leírására és elvezet kozmológiai kérdésekre is. Evvel szemben az általunk feltárt gravitációs kép alapvetően mikroszkopikus.  A részecskék eredetére vonatkozó felfogásunk szerint az enyhén görbült tér óriási számú rendkívül éles és hosszú tüskékkel van felszabdalva, és ezek a tüskék állandóan változtatják helyüket a részecskék mozgását követve. Ezek a tüskék középen üresek, tehát csövek, sugaruk R_c , hosszuk (azaz a görbület) pedig c². Ezeknek a csöveknek a belsejében végzi a részecske sajátforgását. Minden csövet egy enyhe lankás tartomány vesz körül körkörösen, a szokásos gravitációs mező. A lankás részek összegződnek és létrehozzák a csillagok, bolygók és egyéb égi objektumok gravitációs terét. Az összegződő görbületek különösen nagyok a feketelyukakban, ott megközelíthetik a tüskék c² görbületét, de ezt a határt nem haladhatják meg, mert ez tartozik a nullára zsugorodó dimenzió extrém térgörbületéhez. Nem ad meg ilyen határt Einstein gravitációs egyenlete, amelyik extrém körülmények között megenged olyan átmeneteket a téridőben, ami lehetővé tenné a fénysebesség meghaladását (féreglyukak). Nincs azonban olyan csillagászati megfigyelés, amely alátámasztaná ezt a lehetőséget, valószínűleg a fantázia világába kell sorolnunk ezt a jelenséget. Kozmológiai szempontból is problémát jelent az einsteini relativitáselméletben, hogy a térgörbület végtelen lehet, mert ez az Univerzumban szingularitást és végtelenül nagy energiasűrűséget idézne elő. Az általunk felírt görbületi kifejezés viszont elkerüli ezt a dilemmát. A lankás görbületi tartományokkal szemben a tüskék hatása nem összegződhet, mert pozíciójuk nem esik egybe a Pauli-féle kizárási elv következtében.

A térgörbület által létrehozott erőt szemléltethetjük egy gumimatrac segítségével is, amin sok apró üveggolyó van. Tegyünk valahol a matracra egy nehéz golyót, ekkor a golyó környezetében a matrac síkja besüpped. Ebbe a süppedésbe legurulnak az apró golyók, annál gyorsabban minél közelebb vannak a súlyos golyóhoz. Úgyszintén a nagy golyó súlyával arányosan növekszik a süppedés és gyorsabban fognak az apró golyók legurulni. Evvel a példával tudjuk érzékeltetni a szokásos gravitációt, ugyanakkor az erős gravitáció hatását is szemléltethetjük egy másik példával, amikor a rulett asztal vályújába dobunk egy golyót, amelyik többször körbe szalad, amíg a súrlódás nem állítja meg. Az elemi részecskék forgásánál nincs ilyen súrlódás, ezért a forgás fennmarad. Ezekben a példákban a kétdimenziós sík görbülete a harmadik dimenzió irányában valósul meg, de azt már nehezebb szemléltetni hogyan görbül a háromdimenziós tér? Ehhez egy negyedik dimenzióra van szükség, ez pedig az idő! Pontosabban nem az idő, hanem annak szorzata a c fénysebességgel. A negyedik dimenzió c faktora ezért megjelenik a fénysebességű forgások által keltett görbületben is a c² faktor alakjában. Azért szerepel a második hatvány a görbület kifejezésében, mert a görbületet a térkoordináták szerinti második differenciálhányados adja meg. A háromdimenziós tér görbületét úgy szemléltethetjük, hogy a térkoordináták „benyúlnak” az idő dimenziójába. Az általános relativitás elmélete szerint az idő lassabban telik, ahol erősen görbül a tér, ott az „órák lassabban járnak”. Ezért az idő lassulásának térkoordinátáktól való függése jeleníti meg a téridő görbületét.

Az elemi objektumok téridőt „görbítő” hatása makroszkopikusan összegződik és a tényleges görbületi struktúra függ az egyes részecskék térbeli elrendeződésétől, emiatt általános esetben a négy téridő koordináta bonyolultan kapcsolódik egymáshoz, amit Einstein gravitációs egyenlete egy négyszer-négy dimenziós tenzor segítségével ír le. Ez a tenzor határozza meg az egyes tömegpontok mozgását és elrendeződését, viszont a változó elrendeződés visszahat a görbületi tenzorra. Ez a kölcsönös függés okozza, hogy az einsteini gravitációs egyenlet megoldása csak speciális esetekben lehetséges. A mi esetünkben, amikor egyetlen elemi részecske gravitációját írjuk le, nem jelentkezik ez a probléma. Tovább egyszerűsíti a helyzetet, hogy a fénysebességű forgás csak egyetlen dimenziót, az R_c sugarat tartja meg, ezért szorítkozhatunk a sugár és az idő kapcsolatának leírására. 

 Gravitáció és a legkisebb hatás elve

Érdemes összevetni a gravitáció relativitáselméletének kiinduló pontját, mely szerint a gravitációs erő alapja a téridő görbülete, a legkisebb hatás elvével, ami az optikában úgy jelenik meg, hogy a fény különböző törésmutatójú közegen áthaladva olyan utat választ, amelyhez a legrövidebb idő szükséges. Amikor például két optikailag eltérő közeg határfelületén megtörik a fény, a jelenséget az okozza, hogy így lesz rövidebb az a szakasz, amit a fény a sűrűbb közegben tesz meg, ahol lassabb a terjedési sebesség. Erről van szó a gravitáció esetén is, mert a nagy tömeg környezetében erősebben görbül a tér, ami annak felel meg, hogy ott a távolság lerövidül, így az arra haladó másik testnek rövidebb utat kell megtenni. Ezt érzékeljük úgy, hogy az egyik tömeg a másikat maga felé húzza. Fénysebességű forgás miatt a részecske felületén nullára zsugorodik a térpontok távolsága, ezért a részecske saját tömege ezen a gömbhéjon végzi mozgását.

A blog további begyzéseinek összefoglalóját lásd "Paradigmaváltás a fizikában"