A mikrovilág fizikai folyamatainak megértésében alapvető szerepet játszik a szimmetria fogalma, de ez a fogalom is a mindennapok tapasztalatain alapul. Nézzük meg először, hogyan találkozunk a szimmetriával szokásos világunkban, majd vizsgáljuk meg, hogy milyen változáson keresztül megy át a fogalom, amikor világunk legapróbb objektumainak tulajdonságait akarjuk megérteni.

Szimmetria a mindennapi életben

Szimmetriával találkozunk, ha tükörbe nézünk, vizsgálhatjuk arcunk formáját, szemünket, vagy két fülünket, de szimmetrikus a két kezünk és lábunk is, a jobb és a bal egymás tükörképei. Szimmetrikusak lehetnek egy ház ablakai, de szimmetrikusnak találjuk a hópelyheket is, ha közelről vizsgáljuk őket, de megcsodálhatjuk a kristályok szimmetriáit is. Szimmetriáról beszélhetünk, ha két tárgy egymásra rakva, esetleg elforgatva fedi egymást. De minden szimmetria viszonylagos, csak addig érvényes, amíg figyelmen kívül hagyjuk az apró részleteket. Így arcunk se szimmetrikus tökéletesen, de létezik-e világunkban egyáltalán tökéletes szimmetria? A makrovilágban erre a kérdésre egyértelműen nem a válasz, melynek fizikai magyarázata az entrópia fogalmához vezet. A tökéletes szimmetria nagyfokú rendezettséget jelent, de ha a véletlen is szerepet kap, akkor megsérül a rendezett állapot és kisebb nagyobb rendezetlenség jön létre, amelynek fokát jellemzi az entrópia.  Érdemes ezért néhány szót szólni az entrópia fogalmáról is.

Mi az entrópia?

Az entrópia valószínűséget fejez ki. Ha néhány dobókockát feldobunk, annak kicsi a valószínűsége, hogy mindegyik ugyanazt a számot, például hatost mutasson. Mondjuk hat kocka esetén csak egyetlen esetben lehet mindegyik szám hatos, de annak esélye, hogy az egyik ötös legyen már hatszor valószínűbb, mert bármelyik kocka átfordulhat az ötös számra. A kombinatorika matematikai szabályai alapján számíthatjuk ki, hogy az egyes számeloszlások hányszor fordulhatnak elő. Itt most nem célunk matematikai formulákat bemutatni, csak az entrópia fogalmához akarunk közelebb jutni. Ez azt mondja ki, hogy ha teljesen a véletlen határozza meg, hogy milyen számok kerülnek felülre az egyes kockákon, akkor az egyes számkombinációk megvalósulási száma határozza meg, hogy mekkora esély van megvalósulásukra. Ez a valószínűség. Rendezzük el először úgy a kockákat egy szitán, hogy felül ugyanazok a számok legyenek és rázzuk meg a szitát alaposan, akkor meggyőződhetünk róla, hogy milyen ritkán fogunk látni egyforma számokat.

Az entrópia és a valószínűség kapcsolata

Gázokban az egyes molekulák átlagos energiáját a hőmérséklet szabja meg, de ez nem azt jelenti, hogy minden egyes molekula energiája egyenlő lenne, mert ennek valószínűsége épp úgy kicsi, mint ahogy a kockáknál sem valószínű, hogy minden egyes kocka ugyanazt a számot mutassa. Ha az energiát tekintjük rendezőelvnek, azt várnánk, hogy minden molekula energiája minimális legyen, ez lenne a teljes rendezettség. Viszont evvel áll szemben a megvalósulási lehetőségek száma, a valószínűség, amelyik megbontja a rendet. Hogyan tudjuk jellemezni a rendezetlenség mértékét és hogyan alakul a két ellentétes rendező elv viszonya? Erre ad választ a termodinamikában az entrópia fogalma, amit Rudolf Clausius (1822-1888) fogalmazott meg. Eszerint az entrópia a valószínűségtől függ, de nem arányosan, hanem logaritmikusan. Miért lép fel épp a logaritmus, miért nem egyenesen arányos az entrópia a lehetséges a kombinációk számával? Ez egy másik elvre vezethető vissza, amely szerint a gázokban az ütközések gyakoriságát az határozza meg, hogy egy adott hőmérsékleten és egy kiválasztott energiájú állapotban hány molekula tartózkodik. Jelöljük az N(E) függvénnyel az E energiájú molekulák számát, a populációt. A molekulák állandó ütközésben vannak, ami az energia megváltozásával jár együtt, és minél több molekula van egy adott energiaállapotban, annál nagyobb az esély az ütközésre és ezáltal az energia megváltozására, amit egy differenciálegyenlettel fejezhetünk ki:

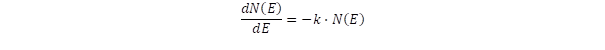
A differenciálegyenlet megoldása szerint a populáció logaritmusa lesz arányos az energiával:

 A negatív előjel annak felel meg, hogy a kisebb energiájú részecskéknek nagyobb a populációja. Ezt az összefüggést a populáció és az energia között nevezzük Boltzmann eloszlásnak, amely a hőmérséklet alapján számítható átlagenergiával veti össze a részecskék számát. Az előbbi érvelés fontos pontja, hogy elvben valamennyi molekula nyomon követhető, azaz megkülönböztethető egymástól.

A populáció és az energia közötti logaritmikus kapcsolatot fogalmazza meg az entrópia az adott energiájú állapot előfordulási valószínűségének logaritmusaként:

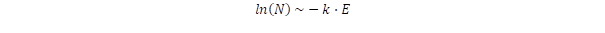
Ebben az összefüggésben k a Boltzmann-állandót jelöli.

Mi az Avogadro szám?

Az entrópia a rendezetlenség irányában hat és ennek mértéke attól függ, hogy hány molekula rendezettségéről van szó. Ez a szám óriási hétköznapi viszonyok között, amelynek nagyságrendjét az Avogadro-féle szám: 6x10²³ adja meg. Ez megmutatja, hogy 18 gramm vízben hány molekula van. Érzékeltessük a szám nagyságát egy hasonlattal. Töltsünk meg egy gyűszűt vízzel és öntsük ki. Képzeljük el, hogy a molekulák nőni kezdenek egész addig, míg akkorák lesznek,. mint egy pingpong labda. Mi fog történni? Ekkor a víz már kifolyik lakásunkból, elárasztja a várost, de folyik tovább, átlép az ország határain, sőt végig fut a kontinensen, beborítja az óceánokat is és csak dagad tovább, amíg elborítja az egész Földet és a végén már csak a legmagasabb hegycsúcsok foglak kilátszani. És ez mindössze egy gyűszű víz! Mivel hétköznapi tárgyaink is ilyen óriási számú molekulából épülnek fel, így rendkívül nagy annak a valószínűsége, hogy sok helyen megbomlik a molekulák szabályos rendje és sérülni fog a tökéletes szimmetria.

A tárgyak megkülönböztethetősége

Van egy másik fontos jellemzője a hétköznapi szimmetriának, ez pedig a megkülönböztethetőség. Bármilyen tárgyról is legyen szó a szimmetria egyes motívumai egymástól függetlenül megfigyelhetők, hiszen minden egyes részletről számtalan foton érkezik szemünkbe. Ez a megkülönböztethetőség fontos szerepet játszik a makrovilágban, de a mikrovilágban gyakran nem érvényesül. Ez utóbbi világban egyrészt a kvantummechanika, másrészt az elemi részecskék elmélete hasznosítja a szimmetria fogalmát, sőt bátran állíthatjuk, hogy szerepe alapvető a mikrovilág kölcsönhatásaiban.

Valószínűség megjelenése a mikrovilágban

Nézzük először az elektronok világát a molekulán belül. Induljunk ki a Hidrogén atomból, ahol egy elektron „kering” a proton körül. A szimmetria formailag hasonló ahhoz, ahogy a Hold kering a Föld körül, aminek lényege, hogy a vonzó kölcsönhatás iránytól független és csak a két fizikai objektum távolsága számít. Mégis van egy döntő különbség: a Hold pozícióját nyomon követhetjük meghatározva az irányt a csillagokhoz képest, de ezt nem tehetjük meg az atomban. Azt mondhatjuk, hogy a Hold mozgásánál az irányok megkülönböztethetők, de ugyanezt nem mondhatjuk az elektronpálya leírásakor. Ezért a Hold pályáját az idő függvényben írja le a klasszikus mechanika, míg az elektronpálya esetén a kvantummechanika csak az irány valószínűségét adja meg a hullámfüggvény segítségével. Hidrogén atomban ez azt jelenti, hogy minden irány egyformán valószínű. A valószínűség oka tehát az irányok megkülönböztethetetlenségében rejlik. A stacionárius elektron állapotokban, amikor tehát az energia nem változik, az idő fogalmát felváltja a valószínűségé. Ha az elektron „keringése” az időben zajlana le, akkor az elektrodinamika szabályai szerint sugároznia kellene, de mivel a pálya a valószínűségi mezőben alakul ki, így az elektronnak sugároznia sem kell. De mi történik, amikor az elektron egy nagyobb energiájú pályáról átugrik egy kisebb energiájúra? Ekkor már időbeli eseményről van szó és emiatt sor kerül foton kibocsátásra is. Minden foton kibocsátás, vagy elnyelés egy ℏ Planck-állandónyi egységgel változtatja meg az elektron impulzusmomentumát, ezért az elektronpályához tartozó impulzusmomentum is csak ℏ többszöröse lehet, ami viszont magával hozza az energiaszintek diszkrét változását.

A szimmetria szerepe a kémiai kötésben

Az atom rendszáma az atommag protonjainak számával egyezik meg és annyi negatív töltésű elektron helyezkedik el a semleges atomban, amekkora a rendszám. A Jupiter holdjainak számát nem korlátozza semmilyen szabály és minden hold pályája külön-külön nyomon követhető, hiszen fotonok serege jut el hozzánk mindegyikről, de ugyanez nem érvényes az atom elektronjai esetén. Ezt fogalmazza meg az elektronok megkülönböztethetetlenségi szabálya. A Jupiter holdjainak mind eltérő pályájuk van, ebben hasonló a helyzet az atom elektronjaival. Ennek analógiája a kvantummechanikában, hogy nem rendelkezhet két elektron azonos kvantumszámokkal (Pauli-féle kizárási elv). Az egyes kvantumszámok az elektronok számára eltérő térbeli valószínűségi eloszlást írnak elő, de ez a tér kiegészül az általunk megszokott háromdimenziós térhez képest. Itt a többletet a spin jelenti, amelyik megduplázza az elektronpályák számát. A pálya-impulzusmomentum „l” kvantumszáma 0, 1, 2, 3 . . .- lehet, ami a spinnel együtt  2·(l + 1), azaz 2, 6, 10, 14 . . . azonos energiájú állapotot hoz létre.   Az elektronok energiáját elsősorban az „n” fő kvantumszám határozza meg (Lásd erről részletesen a „Miért diszkrétek az energia nívók között állapotban” című bejegyzést.) Az atom elektronjai különböző energiájú héjakba rendeződnek. Az egyes héjakon ténylegesen található elektronok számát viszont nem a Boltzmann statisztika mondja meg, hanem a Fermi-féle, amely az elektronok megkülönböztethetetlensége miatt tér el a Boltzmann eloszlástól. Ennek felel meg, hogy csak a legalsó energiaszintek lesznek betöltöttek és az entrópia sem játszik szerepet. Az atommag és az elektronok közötti vonzási potenciál akkor maximális, illetve az elektron rendszer energiája minimális, ha az atommag töltése megegyezik az elektronok számával. Egyes atomoknál ez úgy teljesül, ha egy elektron magasabb energiájú héjba kényszerül, míg másoknál épp egy elektron hiányozhat a betöltött héjhoz. Ilyenkor alakulhat ki ionos kötés, melyben az egyik atom lead egy elektront és így pozitív töltése lesz, míg a másik ezt felvéve negatív iont hoz létre. A kémiai kötésnek azonban nem ez az alapvető formája, hanem a kovalens kötés, amelyik az atomok közötti megosztott pályákon alapul. Ennek magyarázatát egy fontos szimmetria elv adja meg: az időtükrözésé. Az időtükrözéssel szembeni szimmetria alapvetően eltér szokásos világunk tapasztalataitól, ahol alapszabály, hogy a múltba nem lehet visszatérni. A molekulák létrejötte megszünteti a pályák szimmetriáját, ami feloldja az energiaállapotok egyenlőségét, kivéve az időtükrözést. Ez azért fontos, mert így olyan pályák alakulnak ki két atom között, amit két azonos energiájú elektron tölthet be, ami ezáltal lecsökkenti a molekula energiáját.  Ezért úgy fogalmazhatunk, hogy a kémiai kötés alapja a mikrorendszerek időtükrözési szimmetriája.

Paritássértés a gyenge kölcsönhatásban

Lépjünk tovább az atomok és molekulák világából az atommagok és szubatomi részecskék felé, ahol már a gyenge és az erős kölcsönhatás az úr. Itt már a szimmetria a legfontosabb elv, ami meghatározza, hogyan alakulhatnak át az elemi részecskék és milyen erők kötik össze őket. Különösen izgalmas a paritássértés problémája a neutron béta bomlása során, amelyet a gyenge kölcsönhatás idéz elő. Ez olyan, mintha felemelt kezünket a tükörben úgy látnánk, hogy lefelé mutat. Vizsgáljuk meg elektromos és mágneses terek kombinációjával, hogy az elbomló neutronból kilépő elektron és proton milyen pályán halad! Ekkor az energia- és az impulzusmegmaradás törvénye megköveteli, hogy kilépjen egy harmadik nem detektálható részecske is, ez a neutrínó, ami semleges töltése miatt nem hagy észlelhető nyomot a kísérleti berendezésben. Rendezzük úgy át a kísérletet, hogy az elektromos és mágneses terek iránya az előző kísérlet tükörképe legyen! Ekkor azt várnánk, hogy a részecskék pályája a korábbi tükörképe lesz. A tapasztalat viszont a várakozással ellentétes eredményt hozott! Ez azért meglepő, mert bármely más kísérletben, ahol a gyenge kölcsönhatás nem játszik szerepet, csak a gravitáció és az elektromágnesesség, mindig fennáll a paritás, azaz a tükrözés szimmetriája. Helyre áll azonban a szimmetria, ha a tükörkísérletet antineutronnal végezzük el. Tehát az érvényes szimmetriaművelet a térbeli tükrözésen kívül megkívánja, hogy a részecske helyett antirészecske szerepeljen a kísérletben. Ezt hívja a szakirodalom „CP” szimmetriának, amiből „C” a töltéskonjugáció (antineutron bomlásakor a negatív elektron helyett a pozitív pozitron, a pozitív proton helyett a negatív antiproton lép ki), míg „P” jelöli a paritást. Ezt a szimmetriát szemléletesen magyarázza az a javaslatom, amelyben a részecske és antirészecske kettősséget a sajátforgások ellentétes kiralitásával értelmezem (Lásd: „A gyenge kölcsönhatás kiválasztási szabályai és a CPT tükrözés”).

Van azonban az elemi részecskék dzsungelében olyan elemi objektum is, ami még a CP szimmetriának sem engedelmeskedik. A szimmetria azonban helyrehozható, ha az előző két tükrözéseken kívül az idő irányát is megfordítjuk, ez a CPT szimmetria. Az időtükrözés szükségességét az okozza, hogy a tér és idő a relativitáselméletben összekapcsolódik, ezért a teljes tükrözést a négydimenziós téridőben kell végrehajtani.

A blog további írásainak összefoglalása a megfelelő linkekkel együtt megtalálható a „Paradigmaváltás a fizikában” című bejegyzésben