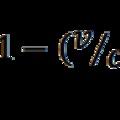Mi az anyag alapvető természete: hullámok vagy részecskék alkotják, vagy egyszerre rendelkezik két látszólag ellentétes tulajdonsággal? Ez a fizika talán legfontosabb és sokáig vitatott kérdése. Simonyi Károly (1916-2001) kitűnő monográfiájában „A fizika kultúrtörténetére” című könyvében foglalja össze a fény hullám, illetve részecske elméletének történetét és ismerteti a végső konklúziót, amit egyrészt a relativitáselmélet, másrészt a kvantummechanika ad meg. Ennek ellenére még ma is találkozhatunk ezt vitató nézetekkel, ezért érdemes ezt a kérdést újra áttekinteni és kiegészíteni a foton mellett a többi részecske kettős természetére vonatkozó ismeretekkel.

Newton és kora

A fény kettős természetének vizsgálata Newtonig (Isaac Newton, 1642-1726) nyúlik vissza, aki nem csak saját korának, hanem az egész fizikának egyik legjelentősebb alkotója volt. A mechanika mozgásegyenletei és a gravitációs törvény megalkotása mellett az optika törvényeit is jelentősen tovább lendítette. Nála még a fizikai különböző jelenségeinek vizsgálata együtt járt a matematikai és filozófiai kérdések tárgyalásával, ami megmutatkozik 1687-ben megjelent főművének címében is : „Principia mathematica philosophiae naturalist”. A tudományt annak egységében látta, erre példa, hogy az optikai törvényeinek – például a fény diffrakciójának – felismerése olyan optikai teleszkóp megalkotásához vezette, amely aztán a csillagászat legfontosabb vizsgálati eszközévé vált.

Newton optikai képének megértéséhez tudni kell, hogy még jóval az elektrodinamika törvényeinek, a Maxwell egyenletek megalkotása (James Clerk Maxwell, 1831-1879) előtt vagyunk, nem is beszélve Planck (Max Planck, 1858-1947) 200 évvel későbbi felismeréséről, amikor a fekete test sugárzás magyarázatához bevezette a foton fogalmát. Logikájának megértéséhez azt is tudni kell, hogy abban az időben még nem vált szét élesen a tudományos, a filozófiai és az okkult gondolkozás.

Newton optikája

Newton 1704-ben megjelent „Optika” című művében a színeket a fény részecskéinek nevezte, amely mögött korpuszkuláris kép volt, azaz apró száguldó gömbök voltak szerinte a fény hordozói. Ebben tükröződött általános természetfilozófiája is, ami könyvében megjelenik: „Kezdetben teremté Isten az űrt és az atomokat”. A részecske koncepció azért jelenhetett meg nála, mert előzőleg a golyók ütközési kísérletei segítették a mechanika törvényeinek megalkotásában. Elképzelése szerint valamennyi fizikai törvény mechanikai eredetű, amely erőcentrumokból és azok hatására létrejövő mozgásokból áll. Optikai elképzeléseit prizmával végzett kísérletei alapozták meg, amelyben a fehér fényt alkotó színeire bontotta. Alaposan ellenőrizte, hogy az egyes színek tovább bonthatók-e prizmákkal, lencsékkel és különböző anyagok átvilágításával és kimutatta, hogy ezek a színek nem bonthatók tovább. Ennél is tovább ment, lencsék és prizmák kombinálásával összegyűjtötte az előzőleg szétbontott színeket és kimutatta, hogy az eredmény ismét a fehér szín lett. Ebből egyértelmű lett, hogy a prizma nem alakítja át a fényt, hanem szétbontja összetevőire, amiket ő a fény részecskéinek tekintett.

Newton magyarázata a fénytörésre

Magyarázatot keresett a fénytörés jelenségére is, megadta annak az okát, hogy ha ferdén éri a sugárzás az üveglapot, vagy a prizma felületét, akkor miért törik meg a fény útja más-más szögben a különböző színek esetén. A jelenséget avval magyarázta, hogy sűrűbb közegben eltérő sebességgel mozognak a különböző fényrészecskék. Magyarázata részben megegyezik mai ismereteinkkel, de abban eltér, hogy ő a sűrűbb közegben a fény felgyorsulásáról beszél. Arra nem volt lehetősége, hogy mérje például üvegben, hogy milyen gyorsan halad a fény, ezért a hang eltérő sebességéből indult ki levegőben és vízben. Mint ismert vízben a hang közel négyszer gyorsabban terjed, mint levegőben. Ennek oka, hogy a hang rezgéseket idéz elő és ennek tovaterjedése sebessége attól függ, hogy milyen gyorsan adható tovább ez a rezgési állapot a közegen belül, ami sűrűbb közegben természetesen gyorsabb.

A fény hullámtermészete: az interferencia

Newton azonban olyan kísérleteket is végzett, amely csak a hullámtermészettel volt magyarázható. Vékony üveglapon (planparalell lemezen) vizsgálta a merőlegesen érkező fény visszaverődését, amit az elülső és a hátsó lapról érkező fény együtt határoz meg. A kísérletben fontos, hogy a fény monokromatikus (egyszínű) legyen és pontosan párhuzamos legyen a lap első és hátsó lapja. A lemez vastagsága és a fény színe (ma úgy mondjuk, hogy hullámhossza) határozza meg, hogy mekkora lesz a visszavert fény eredő intenzitása. Ma már ezt fénymérővel pontosan meghatározhatjuk, ami a vastagság függvényében nulla és 16 százalék körül változik, de Newton természetesen ezt még nem határozhatta meg ilyen pontosan. Viszont így is eljutott a fény térbeli periodikus változásának felismeréséhez. Ma ezt a jelenséget nevezzük a fény interferenciájának. Newton nem jutott el a fény hullámtermészetének kimondásához, hanem a térbeli periodikusságot avval magyarázta, hogy a fény részecskéi előrehaladás közben periodikusan változtatják sebességüket.

Fehér fény esetén is fellép az interferencia, ha például nem egyenletes az üveglap vastagsága, akkor annak két oldaláról visszavert fény helyről-helyre másképp találkozik, ami változatos térképet rajzol ki eltérő színekkel. Mindenütt az a szín jelenik meg, amelynek a hullámhossza kedvező a maximális intenzitás létrejöttéhez. Ugyanezért van, hogy az utca kövezetére kifröcskölt olaj, vagy egy felfújt szappanbuborék is változatos színeloszlást hoz létre.

Az éter fogalom megjelenése

Newton felvetette azt a kérdést is, hogy mi az a közeg, amelyben a rezgés tovább terjed. Hang esetén erre könnyű válaszolni, de hogy lehet, hogy a fény nem csak a levegőn, hanem a vákuumon is áthalad szemben a hanggal? Ezt magyarázta avval, hogy van egy a levegőnél is sokkal ritkább közeg, amit éternek nevezett el és ennek rezgései közvetítik a fényt. Az éterben fellépő erőhatásokra adott magyarázata ma már nem tekinthető tudományosnak, ebben megjelennek az okkult gondolkodás elemei is. Erre már kortársai, így a fénytan megalkotásában szintén jelentős szerepet játszó Huygens is (Christiaan Huygens, 1629-1695)  rámutattak.

Az abszolút tér és idő

Newtonnak az éterre vonatkozó koncepciója szorosan kapcsolódik az abszolút térre és időre vonatkozó elképzeléséhez. Úgy fogta fel a mozgást, hogy ez valamilyen abszolút térhez viszonyítható, amiben az idő is egyenletesen, minden hatástól függetlenül folyamatosan halad előre. Kortársai közül ezt fizikai oldalról Descartes bírálta (René Descartes, 1596-1650), aki csak a testek egymáshoz viszonyított mozgásának látta értelmét, hasonlóan gondolkodott Leibniz is (Gottfried Wilhelm Leibniz, 1646-1716), aki rámutatott, hogy az abszolút térhez való viszonyítás mérésekkel nem igazolható. A relativitáselmélet óta tudjuk, hogy a modern fizika ebben a kérdésben Newton bírálóinak adott igazat.

Huygens hullámfelfogása

De ne menjünk el szótlanul Huygens nagyszerű fénytani felismerései mellett sem, akinek a Newton utáni korszak nem ismerte fel eléggé zseniális meglátását a fény hullámtermészetével kapcsolatban. Ő is a mechanikára vezette vissza a fény terjedését, szerinte az éter finom részecskéi egymást meglökve viszik tovább a mozgásállapotot, amely az előrehaladás során minden pontban egy-egy új gömbhullámot gerjeszt, és a gömbhullámok találkozása hozza létre azt a frontvonalat, ami végül a fény egyenes vonalú terjedését idézi elő. A mai fizikában a kvantumelektrodinamikai leírás valójában ezen az elképzelésen alapul, amit nagyon plasztikusan fejt ki Feynman is (Richard Feynman, 1918-1988)  könyvében: „QED: The strange theory of light and matter”.

Huygens a fénytörést a levegő és az üveg határfelületén mai tudásunknak megfelelően magyarázta a hullámok eltérő sebességével operálva, ahol is eltérő a két közegben a fény hullámhossza (azaz a sebesség és a frekvencia hányadosa). A fény a sűrűbb közegbe érve mindig a merőleges irány felé törik meg, amit helyesen azzal magyarázott, hogy sűrűbb közegben a fény lassabban terjed. Figyelemre méltó Huygens magyarázata a kettős törésről: az izlandi mészpátba beeső fény úgy törik meg, hogy kettőzött kép alakul ki. Helyesen mutatott rá, hogy ez a kristály aszimmetrikus szerkezetéből fakad, ami miatt van két irány, ahol eltérő a fény sebessége. Bár Huygens Newtonhoz hasonlóan az éter részecskéinek mozgásából indult ki, de nem ezeknek a részecskéknek a haladásával magyarázta a fényterjedést, hanem a mozgásállapot továbbterjedésével. Mechanikai alapú modelljéből viszont az következne, hogy a fényterjedés longitudinális rezgés, vagyis a haladás irányában valósul meg. A maxwelli elektrodinamikából viszont tudjuk, hogy a fény tranzverzális elektromágneses hullám, azaz merőlegesen rezeg az elektromos és mágneses mező a terjedés irányához képest.

Descartes fényelmélete

A fény mibenlétére Descartes egy harmadik magyarázatot adott. Ő is az éter és a mechanikai modell alapján értelmezte a fényt, szerinte a mindenséget kitöltő finom anyagrészecskék örvénylése gyakorol nyomást a testekre, ami létrehozza azt a hatást, amit fénynek érzékelünk. Ez az elképzelés is gyorsabb haladást tételez fel sűrűbb közegben, amely ellentmond a fénytörés törvényének. Newton ugyanakkor más okból bírálta ezt az elképzelést, rámutatva, hogy ekkor a bolygók és csillagok mozgását is gátolna ez a nyomás, amely súrlódást hozna létre és ezért megváltoznának a bolygómozgás törvényei.

A Fremat-elv

Newton kortársa volt Fermat is (Pierre de Fermat, 1601-1665), akinek  —  optikai eredményei mellett   — az egyik legfontosabb fizikai elv kimondását is köszönhetjük, amit azóta Fermat-elvnek nevezünk. A különböző optikai közegek közötti törésmutató értelmezésére ő adta a legeredetibb magyarázatot. Huygensszel értett egyet abban a kérdésben, hogy a sűrűbb közeg gátolja a fény terjedését és nem elősegíti, ezért ott lassabban terjed. Ő a fény mozgását mint szélsőértéket képzelte el: a fény mindig olyan utat választ, ami biztosítja, hogy a legrövidebb idő alatt érkezzen meg a célba. Azért törik meg a fény iránya, amikor sűrűbb közegbe érkezik, mert bár emiatt a ritkább közegben hosszabb utat tesz meg, de ezt túlkompenzálja, hogy a lassabb közegben rövidebb lesz az út. Evvel lehetett levezetni a korábbi bejegyzésben („Miért kék az ég? Mindennapi fényjelenségek fizikai magyarázata”) már ismertetett fénytörési törvényt.

Gömbhullámok és a fény egyenes vonalú terjedése

Persze felmerül a kérdés: honnan tudja a fény előre, hogy majd átlép egy másik közegbe, ahol lassabban fog haladni? A kérdésre választ Huygensnek a fény terjedését gömbhullámokkal értelmező modellje adja meg. Egyáltalán miért mozog a fény egyenes vonalban, ha gömbhullámokról beszélünk? Azért mert a tér egyes pontjaiban képződő gömbhullámok között interferencia jön létre és az egyenestől eltérő utak esetén a hullámok fázisa szóródni fog, ami interferencia minimumot hoz létre, szemben az egyenes mentén haladó fényutakkal, ahol a fázisok egyezése interferencia maximumot idéz elő. A fény tehát ’letapogatja’ az összes lehetséges utat, de hatása ott jelenik meg, ahova leggyorsabban eljut az interferencia szabálya miatt. Ugyanez érvényesül, amikor a fény sűrűbb közegbe érkezik, ekkor az egyenes úton az eltérő sebesség miatt szóródni fog a gömbhullámok fázisa, kivéve a leggyorsabb haladást biztosító megtört fényutat. Érdemes itt ismét Feynman kvantumelektrodinamikai magyarázatára utalni, aki nyilak összegzési szabályaival szemlélteti a fázisok szóródását a különböző esetekben.

Maxwell egyenletek magyarázata a fényről

Huygens hullámelmélete ellenére a 18. században uralkodóvá vált a newtoni részecske felfogás, ennek oka, hogy Newton követői leegyszerűsítették és abszolutizálták a nagy géniusz elképzeléseit és figyelmen kívül hagyták, hogy maga Newton is megállapította a fény térbeli periodikus viselkedését. A fény mibenlétének értelmezésében a Maxwell által végső formát nyert elektrodinamikai egyenletek hoztak áttörést a hullámfelfogás javára. Erről szól részletesen a „Mi a fény” című korábbi bejegyzés. Ebben az elektromos és mágneses mező fogalmai játsszák a döntő szerepet, amelyek nemcsak az elektromos töltéssel rendelkező objektumok közötti kölcsönhatást írják le, hanem leírják a fény periodikus változását, azaz a hullámokat is, térben és időben.

A foton fogalmának megszületése

Újabb fordulatot hoztak a fény kettős természetének kérdésében a 20. század fizikai felfedezései. A fizika forradalmát idézte elő Planck hipotézise, amikor a feketetest sugárzás kisenergiájú tartományban a végtelenhez tartó intenzitást úgy tudta elkerülni, hogy bevezette a fény energiájának legkisebb egységét, a fotont. Ez visszatérést jelentett a newtoni részecskekoncepcióhoz anélkül, hogy feladta volna a fény hullámtermészetét. A foton olyan részecske, amely rendelkezik h.ν  energiával (h a Planck állandó), h.ν/c = h/λ impulzussal (ν  a frekvencia, λ a hullámhossz) és ℏ=h/2π impulzusnyomatékkal, és ez a részecske c sebességgel halad. Ez utóbbi tulajdonság eltér Huygens koncepciójától, aki a mozgási állapot tovaterjedését képzelte el az éter finom részecskéi között. Az  impulzusnyomaték létezése viszont térbeli forgásokra utal kapcsolódva a Maxwell egyenletekben szereplő forgó elektromos és mágneses mezőkhöz. A fotont úgy fogjuk fel, amely az elektromágneses kölcsönhatás hordozója.

Az éter létezésének cáfolata a relativitáselméletben

A másik fontos felfedezés Michelson (Albert A. Michelson, 1852-1931) és Morley (Edward W. Morley, 1838-1923) nevéhez fűződik, akik kísérletileg cáfolták az éter létezését, mint az abszolút sebesség viszonyítási alapját. Mérésükben az interferencia jelenségét használták fel, hogy kimutassák a fénysebesség állandóságát a Föld keringési irányához képest. Ebből következik Einstein (Albert Einstein, 1879-1955) relativitáselméletének kiinduló pontja, amely szerint newtoni abszolút tér nem létezik, létezik viszont az abszolút sebesség: a fénysebesség, amely bármely inercia (tehát nem gyorsuló) rendszerből nézve ugyanakkora.

A téridő fogalma

A tér és idő elválaszthatatlan egységet alkot, amit felismerve Minkowski (Hermann Minkowski, 1864-1909) bevezette a négydimenziós téridő fogalmát. A tárgyak hossza már nem a descartesi x²+y²+z², lesz hanem a négydimenziós c²t²-x²-y²-z² mennyiség. Az energia és impulzus is egy négydimenziós kovariánsban kapcsolódik össze. A fenti törvényekből az is következik, hogy a megfigyelőhöz képest nagy sebességgel mozgó tárgyak hosszúsága lerövidül (Lorentz kontrakció, Hendrik Lorentz, 1853-1928)) és megnövekszik a tömegük. Különösen fontos az a határeset, amikor a fizikai objektum sebessége eléri a c fénysebességet: ekkor, ha eredetileg lett volna tömege, ez végtelenül nagyra nőne, ha volt valamilyen fizikai kiterjedése, akkor a mozgás irányában ez nullára csökken.

Beszélhetünk-e a foton tömegéről?

A fénysebességű mozgásból következik, hogy a foton nyugalmi tömege nulla! De a relativitáselmélet legfontosabb eredménye szerint az energia és tömeg egyenértékű, amit az E = m.c² összefüggés fejez ki. Ebből az következik, hogy a foton is rendelkezik tömeggel: m = h.ν/c², de ez nem nyugalmi tömeg, hanem a fénysebességű mozgás által létrehozott mozgási tömeg. Tehát a fénysebességű mozgás a tömeg létrehozója. De mi az a fizikai objektum, ami eredetileg nullatömegű volt, de a fénysebességű mozgás által tömegre tesz szert? Itt én nem keresnék étert, vagy valamilyen misztikus ősanyagot, szerintem a tér egyébként nullatömegű pontjai végzik a c sebességű mozgást. Foton esetén két mozgás kapcsolódik össze, az egyik a transzláció, a másik egy rotáció, amelynek frekvenciája a foton szokásos ν  frekvenciája, amelyik megjelenik az energia kifejezésében. A forgás kerületi sebessége is c, amihez az r = c/2πν sugár tartozik. Ez a sugár véges érték és megegyezik a fény hullámhosszával, mert a Lorentz kontrakció csak a mozgás irányában következik be. A véges sugár, a mozgási tömeg és a c kerületi sebesség pedig magyarázatot ad arra, hogy honnan származik a foton impulzusnyomatéka, azaz a spin (Az okfejtés megtalálható egyéb bejegyzésekben is, például „Az elemi részecskék mozgásformái”, vagy „A tér szerkezete és az elemi részecskék mint rezonanciák”).

Honnan származik a fénysebességű forgást fenntartó erő?

De mi azaz erő, amely fenntartja a körforgást, hiszen kompenzálni kell a kifelé húzó centrifugális erőt! Itt lép be az általános relativitáselmélet koncepciója: a tér görbülete a gravitációs erő forrása. A kör kerülete 2r.π az euklideszi geometriában, de a fénysebességű forgásban a kerület nullára csökken. Tehát egy végtelen mértékben torzult geometriáról van szó! Kimutatható, hogy ez pontosan akkora erőt (ezt nevezem erős gravitációnak, lásd a korábban említett bejegyzéseket) hoz létre, amely kiegyenlíti a centrifugális erőt. A magyarázat megfelel a Fermat-elvnek is. A fotont létrehozó sajátmozgás a legrövidebb utat választja, ez pedig a nullakerületű kör, ahol a térpont forog.

A fény kvantumelektrodinamikai koncepciója

A fény legteljesebb modern elmélete a kvantumelektrodinamika. Ez több is, mint a foton elmélete, mert az elektromágneses kölcsönhatást mint a fotonok és töltéshordozók (például az elektronok) együttesét írja le. Ebben minden fotont és minden elektronállapotot egy oszcillátor ír le, amelyek létrejöttét és eltűnését leíró operátorok képezik a kvantálás második szintjét. Az elmélet legnagyobb sikere az elektron anomális mágneses momentumnak kvantitatív értelmezése. Ez a fizikai állandó a fizika történetének legnagyobb pontossággal mért és elméletileg magyarázott állandója. Az elmélet a Feynman által javasolt diagramokra épül, amelyek számba veszik, hogy milyen átmenetek és átalakulások jöhetnek létre az elektronok és fotonok között beleértve a különböző párképződéseket és annihilációs folyamatokat (elektron-pozitron pár létrejötte fotonokból, és ezek annihilációja). Ezek a diagramok a Huygensi elv továbbfejlesztései, ahol virtuális fotonok és elektronok képződnek és tűnnek el a tér egyes pontjaiban (a virtualitás azt jelenti, hogy kísérletileg nem detektált, de a kölcsönhatás mértékét meghatározó folyamatokról van szó). Feynman már idézett könyvében veszi sorra ezeket a lehetséges folyamatokat és mutat rá, hogy ebben sem a fénysebesség, sem az oksági elv nem jelent korlátot. Van például olyan folyamat, ahol egy foton előbb hoz létre egy elektron-pozitron párt, mint ahogy maga létrejön.

A részecskék fénysebességű forgásmodellje

 Feynman arra az álláspontra helyezkedik, hogy nem lehet semmilyen fizikai képet megadni a bonyolult folyamatokra, elégedjünk meg vele, hogy vannak jól működő egyenleteink. A magam részéről nem adnám fel a lehetőséget, hogy konzekvens fizikai képet rendeljek a jelenségekhez, amit már az említett korábbi bejegyzésekben ismertettem. Itt most összefoglalom a modell főbb pontjait.  A fotont, ahogy leírtam, egy csavarmozgás ábrázolja a térben egy henger felületén. Ennek mintájára az elektron is csavarmozgás egy gömbfelületen, ahol két forgás kapcsolódik össze. A két forgás egymáshoz képesti viszonya a jobb és balsodrású királis szimmetriával értelmezhető, ami megfelel a negatív töltésű elektronnak és a pozitív töltésű pozitronnak. Az elektron és pozitron találkozása annihilációhoz vezet, mert ekkor az ellentétes kiralitású két ’másodlagos’ forgás kioltja egymást és az így megmaradó egyszeres forgás épp a fotonnak felel meg. A fénysebességű forgások nullafelületű gömböt hoznak létre összhangban az elektron és pozitron szórás kísérletekkel (Bhabha-szórás, Homi K. Bhabha, 1909-1966), amely szerint a részecske töltése pontszerű eloszlással rendelkezik. Az elektron spinje fele a fotonénak, mert az erős gravitációnak két különböző forgásból származó centrifugális erőt kell kiegyenlíteni. Már számos kísérlettel igazolták, hogy a fotonhoz hasonlóan az elektron, a proton, sőt kisebb molekulák is kettős természettel rendelkeznek, egyaránt viselkednek korpuszkulaként és hullámként. Az interferencia jelenség hullámhossza a Compton hullámhossz (Arthur H. Compton, 1892-1962), amely a nyugalmi tömegből számítható ki a l = h/m.c összefüggés alapján. Az elektron fénysebességű forgásmodellje ezt a hullámhosszat a forgás sugaraként értelmezi, amely meghatározza az elektron-hullám interferenciaképét.

Virtuális részecskék a virtuális térben

Hogyan kapcsolhatjuk fizikai világképünkhöz a kvantumelektrodinamika virtuális folyamatait? Kétségtelen, hogy szükséges számba venni ezeket a folyamatokat, ha az elektron és a mágneses mező kölcsönhatását helyesen akarjuk leírni, viszont mivel nem detektálható folyamatokról van szó, így az a tér és idő, amelyben leírjuk a folyamatokat szintén virtuális. Ezt a virtuális teret és időt már nem korlátozzák azok a törvények, amelyet a valódi kölcsönhatásokon keresztül ismertünk meg, ezért nem vonatkozik rájuk az oksági elv és a fénysebesség átléphetetlenségi szabálya sem. 

Összefoglaló megjegyzés

Az elemi részecskék és a fény kettős természetére szemléletes magyarázatot ad a fénysebességű forgások modellje. A hullámtermészet onnan származik, hogy minden részecske, így a foton is fénysebességű forgásokat végez, melynek fázisegyezése alakítja ki az interferencia maximumokat. A fénysebességű forgáshoz azonban véges sugár és tértartomány tartozik, ez reprezentálja a korpuszkuláris tulajdonságokat, a tömeget, az impulzus és az impulzusnyomatékot.

A blog egyéb írásainak összefoglalója a megfelelő linkekkel együtt a „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv” című bejegyzésben található meg.