A Newton és Coulomb törvények

A címben szereplő két kölcsönhatás jellege sokban hasonlít, hiszen mindkét erő az r távolság négyzetével csökken és egyaránt arányos a fizikai objektumra jellemző két mennyiség szorzatával, ami a gravitációnál az objektumok m tömege, az elektromos kölcsönhatásnál a q elektromos töltés.

A gravitációs erő Newton által megadott alakja:

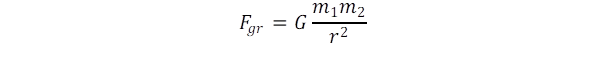
ahol G = 6,674.10^-11m³/kg.s²

Az elektromos erőhatás törvényét két töltés között Coulomb adta meg:

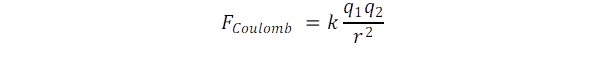
Itt a k együtthatót szokás egységnek választani, ha a két töltést épp az erőtörvény segítségével definiáljuk. Tömegvonzás esetén ez nem bevett gyakorlat, mert először definiáljuk a tömeget mint tehetetlenséget a szintén Newton által megfogalmazott gyorsulási törvény szerint, ahol a tömeg az F erő és az általa létrehozott gyorsulás hányadosa:   m = F/a.

A kölcsönhatási erő kiváltó oka és tárgya

A két erőtörvény abban is hasonló, hogy szimmetrikus szerepet tölt be az erőhatás kiváltó oka (például m₁ és q₁) és az erőhatás tárgya (például m₂ és q₂), azaz a vonzhatóság, vagy taszíthatóság. Annak külön jelentősége van, hogy nincs „kevert” kölcsönhatás, amikor például az m₁ tömeg vonzása a q₂ töltésre hatna. A kétféle kölcsönhatás tehát teljesen elkülönül.

Az erők pontszerű forrása

A két kölcsönhatás távolságfüggése arra utal, hogy mindkettő a fizikai objektum egyetlen matematikai pontjából indul ki és a hatás gömbszerűen terjed, amiért annak csökkenése a gömb felületével arányosan csökken. Ezt fogalmazhatjuk meg az erővonalak törvényével, amely szerint az erővonalak száma nem változik és ezért felületi sűrűsége a felülettel fordítva arányos. Ez nem triviális, mert a nukleáris erős és gyenge kölcsönhatásban az erővonalak eltűnnek az atommagok méretét meghaladó tartományban.

A két törvény további közös vonása, hogy nincs megszabva a távolságra alsó határ sem, tehát elvben nulla távolságra is vonatkozik, ahol az erő már végtelenül nagy lehetne. Itt felmerül, hogy mi az a lehető legkisebb távolság, amilyen közel kerülhet egymáshoz két fizikai objektum, van-e valamilyen saját sugár, ami megakadályozza a további közeledést? Ha van, akkor ez egy további erőhatást jelent, ami az elektromágneses kölcsönhatásnál erősebben választja szét a fizikai objektumokat. Voltaképp ilyen erőhatásnak tekinthetjük a kvantummechanikában a bizonytalansági elvet, ami nem teszi lehetővé, hogy egy fizikai objektum pozíciója és impulzusa egyidejűleg tetszőleges pontos értéket vegyen fel. (Lásd: „Határozatlansági relációk a kvantummechanikában”). A pontszerűség elve komoly gondot okoz a mezőelméletben, amikor végtelen értéket ad az elektron elektromágneses sajátenergiájára.

Vonzás és taszítás a kölcsönhatásokban

Az elemi részecskék világában a gravitáció elhanyagolható, mert erőssége mintegy negyven nagyságrenddel kisebb az elektromos erőhöz képest. Elvi szempontból azonban nem is a nagyságrend a fontos, hanem az, hogy a kölcsönhatási erő az egyik esetben mindig vonzást hoz létre, míg a másik esetben lehet vonzás és taszítás is, amit a töltés előjelével írunk le. A gravitáló tömeg viszont mindig pozitív.

Mágneses kölcsönhatás mint relativisztikus effektus

További különbség, ami azonban csak látszólagos, hogy létezik külön elektromos és mágneses kölcsönhatás, míg erről nem beszélünk a gravitáció esetén. Később azonban látni fogjuk, hogy ennek pusztán gyakorlati oka van. További különbség, hogy a tömeget nem csak a gravitáció útján értelmezhetjük, hanem a gyorsítással szembeni tehetetlenségen keresztül is. A gyorsításhoz erőt kell alkalmazni Newton második törvénye szerint, ami arányos a testre jellemző állandóval, amit tömegnek nevezünk. Pont evvel a tömeggel arányos a test által létrehozott gravitációs erő is, amit Eötvös József nagy pontossággal mutatott ki torziós inga kísérletével.

Rendelkezik-e az elektromos töltés is „tehetetlenséggel” a gyorsítással szemben? A válasz ekkor is igen! Gyorsítjuk fel az elektronokat egy ciklotronban egy körpályán (itt jegyezzük meg, hogy állandó kerületi sebesség esetén is gyorsulásról beszélünk az állandó irányváltozás miatt, ami egyenesen arányos a kerületi sebesség négyzetével, fordítottan a sugárral és létrehozza a centrifugális erőt). Ekkor az elektronok sugározni fognak, amit fékezési sugárzásnak nevezünk és a veszteség pótlásához szükséges erő arányos lesz a gyorsulás és a töltés szorzatával. Ez teljes analógiát jelent a Newton törvénnyel, ahol a gyorsító erő a tömeg és a gyorsulás szorzata. Mégis van egy fontos különbség: amíg a tömeg gyorsítását nem kíséri semmilyen sugárzás, addig a töltés esetén ez sugárzás kibocsátásával és ezáltal energiaveszteséggel jár.

Diszkrét energiaállapotok kötött állapotban

Azokban a mozgásokban, amikor a gravitációs erő gyorsítja a tömeget –  ennek egyik formája, ahogy a bolygók keringenek a Nap körül – a mozgás nem jár energiaveszteséggel. Ha a pozitív és negatív töltésű objektumok között hozunk létre hasonló körmozgást, akkor a sugárzás miatt elvész az energia és előbb-utóbb megszűnik a körmozgás. Ennek az elvnek mond ellent a Bohr-féle atommodell, amelyik a negatív elektronokat a pozitív atommag körüli körpályán képzeli el sugárzási veszteség nélkül. Az ellentmondást a kvantummechanika oldja fel, mert a sugárzást adagokhoz, kvantumokhoz köti, és nem engedi meg, hogy az elektron beleessen a magba. (Lásd: Miért diszkrétek az energianívók kötött állapotban” és „Foton: a mikrovilág postása és szabályozója”) A foton kvantum kibocsátása rezonancia feltételekhez kötött, a magasabb energianívókról bizonyos valószínűséggel az elektron foton kibocsátással alacsonyabb nívóra kerülhet. A fotonkibocsátás ezért nem folytonos folyamat. Hogyan egyeztethető össze ez a kép a ciklotronban keringő elektronokkal? Ott az elektronok nem alapállapotban mozognak a mágneses mező fogságában, ezért bizonyos valószínűséggel alacsonyabb energiájú pályára ugranak és mivel igen nagyszámú elektronról van szó, így a gyakorlatban folytonos sugárzásról beszélhetünk.

Lehetnek diszkrét energiaállapotok gravitációs térben is?

Kötött állapotban az elektronok és az elektronok által a molekulához kötött atomok diszkrét energia nívókat hoznak létre (lásd a négyrészes bejegyzést: „Miért diszkrétek az energianívók kötött állapotban?”. Vajon, ha egyedi részecskék gravitációs térben való mozgását vizsgáljuk, akkor szintén létrejönnének diszkrét energianívók, más szóval lehet-e kvantumos a gravitáció? Képzeljük el, hogy átfúrjuk a Földet az Északitól a Déli sarokig és vákuumot hozunk léte a lyukban, majd elejtünk egy semleges részecskét, például egy neutront. Erre a Föld gravitációs ereje fog hatni, ami legnagyobb a Föld felszínén, majd lefele haladás során a gravitáció csökken és nulla lesz, amikor a részecske a Föld középpontjába ér, majd onnan továbbhaladva a gravitáció visszafelé húzza a neutront , amíg eléri a Föld túloldalát, ahol elfogy a neutron kinetikus energiája és újra esik lefelé. Így hasonló oszcilláció jön létre, mint amikor a vegyértékrezgést vizsgáljuk a molekulában, ahol a Hook törvény szerint a megnyúlással arányosan növekszik a húzóerő. Vegyértékrezgésnél az erőállandó és a tömeg arányával kifejezett frekvencia játszik szerepet, és a kvantummechanika diszkrét energianívókat határoz meg, amelyek különbsége a frekvencia és a h Planck-állandó szorzatával adható meg. Evvel szemben a klasszikus mechanika szerint az energia folytonosan változik. Vajon melyik leírás helyes a neutron oszcillációja esetén? Felhozhatunk más példát is, például egy légkör nélküli bolygó, vagy a Hold körül állítsunk szintén egy neutront keringési pályára. A mozgás kvantummechanikai analógiája az elektronok pályája a pozitív töltésű atommag körül. Vajon itt a klasszikus Kepler törvények írják le a mozgást, vagy a kvantummechanikai egyenletek? A kérdés azért jogos, mert matematikai szempontból azonosak az erőhatások, bár az egyik esetben az elektromos erő, a másikban a gravitációs erő játszik szerepet. A magyarázatot a foton szerepe adja meg. Mivel a gravitációs térben való mozgás során nem kerül sor foton kibocsátásra, így a foton kvantumos tulajdonságai nem játszanak szerepet és ennek folytán a neutron mozgását a klasszikus mechanika törvényei határozzák meg.

Ellenőrizhető-e gravitációs térben a neutron diszkrét energiája?

Fölvetődik a kérdés, hogy van-e kísérleti lehetőség, hogy eldöntsük diszkrét, vagy folytonosan változó a neutron energiája, ha gravitációs térben halad? A neutron rendelkezik mágneses nyomatékkal, tehát mágneses mezőben kölcsönhatást gyakorolhatnánk rá. De ekkor már nem tisztán gravitációs kölcsönhatás érné, így a mérés már nem a gravitációs mezőben kialakuló energianívókról adna felvilágosítást. Ha a neutron más részecskével ütközik, akkor is az elektromágneses kölcsönhatás határozza meg az ütközés eredményét. Az egyes neutronok gravitációs mezeje pedig olyan gyenge, amiért nem hoz létre mérhető hatást. Ezért a neutronok esetleges diszkrét energiája csak elvi jelentőségű kérdés, amely eldönti, hogy a gravitáció lehet-e kvantumos természetű.

Van-e a gravitációnak is „mágneses” komponense?

Korábban felvetettem a kérdést, hogy amíg az elektromágneses kölcsönhatásban két mezőről beszélünk, hasonlót nem említünk a gravitáció során. De honnan származik a mágneses mező? Ennek eredete a fény véges terjedési sebességéhez kapcsolódik, ami késleltetést okoz az elektromos hatás megjelenésében. Mozogjon például az elektron az összekötő egyenesre merőlegesen egy másik töltött objektumhoz képest. Ha az elektron távolsága a másik töltéstől d, akkor az erőhatás t = d/c idővel később érkezik meg. Ez alatt a v sebességű elektron helyzete megváltozik, a korábbi pozícióhoz képest s = v.t = d.v/c távolságra kerül. Emiatt a vonzóhatás nem a valódi helyről, hanem onnan eltérő irányból érkezik, amit úgy foghatunk fel, hogy a tényleges erő két komponensből tevődik össze, az egyik az elektromos, a másik az arra merőleges erő, amit mágneses mezőnek nevezünk és a mágneses mező által kifejtett hatás (Lorentz erő) nagysága az elektromos erőhöz képest v²/c² arányában kisebb lesz. Mivel a gravitáció terjedési sebessége szintén a c fénysebesség, így a gravitáció hatása is késleltetve érkezik, aminek értéke szintén v²/c²-szer lesz kisebb a gravitációnál. Például a Föld keringési sebessége tízezerszer lassabb, mint a fénysebesség, így ez a késleltetett gravitációs hatás száz milliószor gyöngébb, mint amekkora erővel a Nap a Földet vonzza. A földi gyakorlatban ez elhanyagolható, de a pontos pályaszámításokban már ez is szerepet játszik.

Az elektromágneses és gravitációs mező négydimenziós térben

A modern fizika egyik fontos célkitűzése, hogy egybe gyúrja az elektromos és a mágneses kölcsönhatást. Erre Kaluza tett egy érdekes kísérletet, amikor a szokásos háromdimenziós teret kiegészítette egy negyedikkel és így képes volt a két kölcsönhatást egységes keretek között leírni. A baj csak az volt, hogy az elképzelés kizárólag a klasszikus fizika keretei között működik és nem volt kiterjeszthető a kvantummechanikára. Ezen nem is kell csodálkozni, ha arra gondolunk, hogy a gravitáció nem kvantumos, hanem folytonos. Később Kaluza ötlete nagy keletre tett szerint a húrelméletben, de a kvantálás itt sem jött össze, ezért elkezdték szaporítani a dimenziókat, amely a legújabb elméletekben már 26-nál tart, de konzekvens matematikai kép máig sincs.

A gravitációs és elektromágneses mező értelmezése háromdimenziós térben

A blog különböző írásaiban írtam le saját elképzelésemet a részecskék fénysebességű forgásairól, amely a szokásos háromdimenziós tér keretei között ad magyarázatot az elektromos és a gravitációs kölcsönhatás közös eredetére, az elmélet főbb vonásait itt is ismertetem.

A kiindulópont Einstein speciális és általános relativitáselméletének két alapelve: a fény terjedési sebességének függetlensége a vonatkoztatási rendszertől, illetve a gravitáció visszavezetése a tér görbületére. Az előbbi elv megköveteli a tér és idő összekapcsolását, amely szerint a geometriai hosszúság a vonatkoztatási inercia rendszer sebességétől függ, amit a Lorentz-kontrakció ír le. Körmozgás esetén ez azt jelenti, hogy a kör kerülete nem 2r.π, ahogy azt az euklideszi geometriában megszoktuk, hanem ennél kisebb lesz, maga a sugár azonban nem változik, mert ez merőleges a mozgás irányára. A kerület rövidülése jellemzi a tér görbületének mértékét. Ha most a bolygómozgás Kepler-szabályából indulunk ki, akkor kimutatható, hogy a görbület alapján levezethető a Newton-féle gravitációs erő.(lásd: „Térgörbület és gravitáció forgó rendszerekben”, illetve „Fénysebességű forgásokés a relativitáselmélet”. Ha a körmozgás kerületi sebessége a c fénysebesség, akkor a kerület hossza nulla lesz: ez jelenti a tér maximális görbületét és ekkor a gravitációs erőhöz tartozó potenciális energia m.c² lesz, egyezésben az energia és a tömeg ekvivalenciájának törvényével. Fotonok esetén az energiát a h.ν  reláció adja meg (h a Planck-állandó és ν  a frekvencia), ezért felhasználva a relativitáselmélet legfontosabb egyenletét:  m.c² = h.ν  a mozgási tömeget a frekvenciával fejezhetjük ki: m = h.ν / c². Ez a frekvencia a körmozgás frekvenciája, ami meghatározza a kerületi sebességet: c = r. 2πν . Ezt felhasználva a tömegre: m = h/(2 π.r.c) = ℏ/r.c összefüggést kapunk. Ekkor a foton impulzusa p = m.c = ℏ/r és impulzusnyomatéka I = p.r = ℏ lesz. Az impulzusnyomaték, azaz ennek együtthatója a spin tehát a forgási frekvenciától függetlenül mindig azonos lesz és egyezik a ℏ redukált Planck-állandóval. A fénysebességű modell tehát megalapozza a hullámmechanikát, mely szerint: a kvantum eredete a fénysebességű forgás.

Az m tömegű és c kerületi sebességgel forgó rendszerben fellépő centrifugális erő F_cf = m.c²/r = ℏ.c/r², ezt ellensúlyozza a térgörbületből származó erő, amit erős gravitációnak nevezek. A foton képződése tehát önfenntartó forgás, ahol a forgás okozta görbület centripetális ereje tartja egyensúlyban a forgás centrifugális erejét.

Az anyag és antianyag kettősségének magyarázata

A foton létrejötte tehát körforgással magyarázható, amely együtt jár a forgástengely mentén történő fénysebességű terjedéssel, ami hengerfelületen való csavarmozgásnak felel meg, ahol a csavar menethossza a fény hullámhosszát adja meg. Más a szimmetriája az elektronnak, vagy a fermionoknak, melyek gömbszimmetrikus alakzatok, amit két fénysebességű forgás kombinációjával értelmezhetünk. Ekkor a gömb felszíne nulla lesz az euklideszi geometria 4π.r² nagysága helyett. Itt 4π jelenik meg a képletben a kör kerületét meghatározó 2π helyett, amiért az impulzusnyomaték is feleződik és ℏ/2 lesz. Ez magyarázza, hogy az elektron spin miért S = ½. De nem csak a spin értékére kapunk magyarázatot, hanem az is érthetővé válik, hogy miért létezik anyag és antianyag: a két forgás egymáshoz képest két sodrásirányt vehet fel, az egyik a bal kéz, a másik a jobb kéz szimmetriájának felel meg.

Miért nem lesz végtelen a sajátenergia?

A fénysebességű forgás koncepciójában fontos szerepet tölt be a véges r = c/2πν  = ħ/m.c Compton-sugár, amely kettéválasztja a részecske belső és külső tartományát. A gravitációs mező és az elektromos mező a külső tartományra vonatkozik, ezért nem értelmezhető a gömb belsejében. Ezáltal szabadulunk meg a mező elméletek végtelent adó sajátenergiájától, mert nem kell számításba venni a kölcsönhatásoknak az véges r sugárnál rövidebb tartományát.

A töltés forrása a Coriolis erő

Lépjünk tovább az elektromágneses erők világához, mert a modell erre is világos magyarázatot ad. Forgó rendszerekben a centrifugális erőkön kívül fellép a Coriolis erő is, ha van a rendszeren belül egy további mozgás is. Erre példa földi viszonyok között, ahogy a sarkoktól az egyenlítő felé haladó levegő- és vízáramlatok útja elcsavarodik. A kéttengelyű forgásoknál a „második” forgásra hat ez az erő, amelynek nagysága F_Coriolis = ±m.c²/r = ±ℏ.c/r², ez ugyanakkora, mint a centrifugális erő, de előjele lehet pozitív és negatív a sodrásirány függvényében, ami magyarázza, hogy a pozitron töltése miért ellentétes az elektronnal. A Coriolis-erő nem kifelé mutat, mint a centrifugális erő, hanem csavarásmozgást hoz létre. Evvel összhangba kerültünk a kvantumelektrodinamika felfogásával, amelyben az elektromos erőt a virtuálisan kibocsátott fotonok közvetítik, hiszen a csavaró erő épp egytengelyű forgásokat, azaz foton kvantumokat hozhat létre. Ennek az erőhatásnak a külső térben van egy csillapítási tényezője, a Sommerfeld-féle α = 1/137 állandó. A Coulomb kölcsönhatás az elemi töltéssel rendelkező fermionok között:

A tömeg mint a tehetetlenség és a gravitáció forrása

Az elektromos töltés tehát a kettősforgások képessége, hogy egytengelyű fénysebességű forgásokat, azaz foton kvantumokat bocsássanak ki, de most nézzük meg, hogyan magyarázzuk a tömeget mint tehetetlenséget az erőhatással szemben?

Minél nagyobba fénysebességű forgások frekvenciája, annál kisebb lesz a karakterisztikus sugár, és annál nagyobb lesz a tömeg és a tér görbülete. A mozgás Newton törvénye szerint nem lép fel erő az egyenletes sebességű mozgásoknál, ha nincs közegellenállás, vagy súrlódás. Ez abból fakad, hogy nem létezik „éter”, ami kitöltené a teret és akadályozhatná a mozgást. A mozgás sebességének nincs is „abszolút” nagysága, ami a részecske mozgását, azaz értelmezésünk szerint a fénysebességű forgás által létrehozott extrém görbület helyváltoztatását jellemezné. Kivételt csak a fénysebességű mozgás jelent, ahol azonban nem beszélhetünk nyugalmi tömegről. A tehetetlenséget úgy foghatjuk fel, mint a tér a priori ellenállását az extrém görbületek gyorsuló átrendezésével szemben; és minél nagyobb a görbület, annál nagyobb erő kell a gyorsításhoz. Másként szólva a tehetetlenség a tér alapvető szerkezeti tulajdonsága. Egyenletes sebességű mozgáshoz csak akkor kell erő, ha más objektumok gravitációs, vagy elektromágneses erőterében való elmozdulást idézünk elő. Ha nincs ilyen erőtér, akkor az extrém térgörbület, azaz a részecske helyéről nincs értelme beszélni.

A kettősforgások által keltett térgörbület maga körül kismértékű torzulást hoz létre, amely arányos az extrém görbülettel, azaz a tömeggel és mértéke a távolság négyzetével csökken. Ez a szokásos gravitációs mező. Ez a folytonosság elvéből következik, mert a tér görbületéről is feltételezhetjük a folytonosságot. Ez egyúttal feltételezi egy keskeny tartomány létezését, amelyben az extrém görbület átmegy a fénysebességnél sokkal lassabb Kepler forgások által keltett kismértékű görbületbe. Azaz a folytonosság megköveteli egy nagyon keskeny átmeneti tartomány létezését, amely egy rövid hatótávolságú kölcsönhatásnak felel meg, ez a gyenge kölcsönhatás, amely a standard modell szerint valamennyi részecske esetén szerepet játszik.

Folytonosság és kvantumosság a kölcsönhatási mezőkben

Meggondolásunk lényege, hogy a kvantum elv csak az elektromágneses kölcsönhatásra vonatkozik, míg a gravitáció a folytonosság elvére épül.  Ezért nincs olyan kölcsönhatás, amit a bevezetőben említettünk, ahol kevert módon lépne fel a töltés és a tömeg. Ez a kép arra is világos magyarázatot ad, hogy miért sikertelenek azok a próbálkozások, amelyben a gravitációra is kvantumos magyarázatot akarnak adni.

Kiegészítésként megjegyzem, hogy a kvantum elv alapvető a gyenge és erős nukleáris kölcsönhatásban is, de ezt a kérdést máshol tárgyalom, lásd például „Az elemi részecskék mozgásformái”, illetve „Az egységes fizikai világkép” című írásokat.

A blog egyéb írásainak összefoglalása a megfelelő linkekkel megtalálható: „Paradigmaváltás a fizikában”.