A kvantummechanika áthághatatlan korlátot állít a mérési pontosság számára: például egyidejűleg nem lehet tetszőleges pontossággal meghatározni egy kvantummechanikai objektum pozícióját és impulzusát. Ezt szokták szemléltetni hullámcsomaggal, amikor a csomag hossza egyaránt limitálja a pozíció és az impulzus pontosságát, de széles köre van olyan kísérleteknek, ahol az elvi határ visszavezethető optikai törvényekre. Másik gyakori példa, amikor az állapot élettartama korlátozza az energiamérés pontosságát. Az absztrakt matematikai levezetés megtalálható különböző kvantummechanikai tárgyú könyvekben, példa rá Geszti Tamás kitűnő műve: „Kvantummechanika”, Typotex, 2014.

Itt most nem célunk a levezetés teljes ismertetése, csupán a sarkalatos pontokra mutatok rá, amelyből elvi következtetéseket lehet levonni.

A fizikai mennyiségeket hermitikus operátorok reprezentálják, ahol a hermitikusság biztosítja, hogy a sajátértékek valós számok lesznek. Ha A és B két ilyen operátor, akkor a várható érték körüli szórásból képzett  ΔA és ΔB hibákra a következő egyenlőtlenség állítható fel:

ΔA.ΔB ≧ ½<│A.B – B.A│>

Tehát két különböző fizikai mennyiség szorzatának hibája a két operátor kommutátorával határozható meg. Viszont bármely ξ változóból és annak deriváltjából képzett kommutátor olyan operátort alkot, amelynek sajátértéke az 1 szám és sajátfüggvénye tetszőleges, ugyanis a szorzatfüggvényekre vonatkozó deriválási szabály miatt:

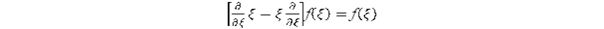
Ha ξ a pozíciót reprezentálja és deriváltját szorozzuk ℏ/i konstanssal, akkor az impulzus és a pozíció közötti határozatlansági relációt kapjuk meg: Δp.Δr ≧ ½ ℏ. Ugyanígy kapjuk meg az időtartam és az energiamérés hibája közötti relációt. A határozatlanság tehát annak a következménye, hogy az impulzus és energia operátorában a véges ℏ állandót választottuk a differenciálok együtthatójának, ez a választás pedig a foton kvantált természetéből következik.

Végeredményben tehát bármely kvantummechanikai objektum impulzusára és pozíciójára vonatkozó határozatlanság az információ hordozójának, azaz a fotonoknak kvantált természetéből ered. Ugyanez vonatkozik a mikroállapot időtartama és az energiamérés pontossága közötti határozatlanságra is. A határozatlanság azonban nem jelenti a pozíció és az impulzus bizonytalanságát, hanem a mikro rendszerről szerezhető információ korlátozottságát mutatja. Külön-külön ugyanis a pozíció és az impulzus tetszőleges pontossággal meghatározható. Például, ha nagy energiájú fotonokkal vizsgáljuk az objektumot, akkor leszoríthatjuk a pozíciómérés hibáját, de ekkor akkorát „lökünk” az objektumon, hogy az impulzusról szerzett információnk lesz bizonytalan. Minden mérésben fotonokat figyelünk meg, gondolkozásunkban azonban szétválasztjuk az információ hordozóit és azt az objektumot, ahonnan a fotonok érkeznek. A határozatlanság azt fejezi ki, hogy ez a szétválasztás a Planck állandó mértékében önkényes. A kvantummechanika egy olyan fizikai elmélet, amelyik hallgatólagosan tudomásul veszi ezt a határozatlanságot és az állapotfüggvény által megfogalmazza a folyamatok valószínűségi jellegét. Az „EPR paradoxon” című bejegyzésben kerül ez a gondolat részletes kifejtésre.

Kvantummechanikai inercia erő

A „Miért diszkrétek az energianívók kötött állapotban” című bejegyzésben az oszcillátorok nulla ponti rezgését a kvantummechanikai bizonytalansági elvre vezettük vissza, és ugyanez az elv magyarázza, hogy miért nem egyesül az elektron a hidrogénatom protonjával a közöttük lévő Coulomb vonzás végtelenhez tartó nagysága ellenére. A jelenséget megvilágíthatjuk más szemszögből is bevezetve a bizonytalansági elvből származó tehetetlenségi erő fogalmát. Kötött rendszerekben a mindenkori vonzóerő egyensúlyban van a gyorsuló mozgások által keltett tehetetlenségi erővel. Erre példa körmozgásokban a centrifugális és a centripetális erők egyensúlya. Felvetjük a kérdést, hogy mekkora tehetetlenségi erő származtatható a bizonytalansági relációnak megfelelő kinetikai energia ingadozásából.

Az impulzus- és a helykoordináták közötti bizonytalansági elv szerint: Δr.Δp ≧ ℏ. (Itt a könnyebb áttekinthetőség kedvéért elhagyjuk az ½ együtthatót). Emiatt a kinetikus energia bizonytalansága ΔE_kin = Δp²/2m ≧ ℏ²/(2m.Δr²) . Az erő definíció szerint a potenciális energia negatív gradiense, ennek mintájára a tehetetlenségi erőt, mint a kinetikus energia negatív gradiensét értelmezhetjük:

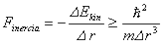
A centrum körüli oszcilláció esetén az ingadozás amplitúdóját azonosnak vehetjük a kitéréssel, azaz Δr = r. Az így értelmezett tehetetlenségi erő gyorsabban növekszik kis távolságban, mint a Coulomb erő, hiszen az előbbi a távolság harmadik, az utóbbi pedig második hatványával arányosan csökken. Emiatt, ha az elektron a kritikus távolságnál közelebb kerül az atommaghoz, akkor a taszító erő meghaladja a vonzóerőt, és így a proton nem ejtheti foglyul az elektront. Az erők egyensúlyi feltétele szerint

Az erők egyensúlyából számolható sugár r₀ = ℏ²/(m.e²) megegyezik a Bohr rádiusszal. Ez az elektron legkisebb pályasugara, ahol a mozgás tisztán oszcillációs jellegű, ezért az erő egyensúlyban nem lép fel a centrifugális hatás. Nagyobb pályasugarak esetén a centrifugális erő járuléka is megjelenhet, sőt dominánssá válhat, mert a bizonytalansági erő a centrumtól való távolság függvényében gyorsan csökken. Ekkor közeledünk a klasszikus képhez, amit jól ír le az eredeti Bohr modell. Klasszikus határesetben a bizonytalansági erő elhanyagolható, és mivel a Coulomb és a centrifugális erő távolságfüggése meggegyezik, így az egyensúly bármekkora sugár esetén megvalósulhat, az energia pedig folytonosan változik. 

Az  inercia erőt  a nem-relativisztikus kinetikus energiából származtattuk. A relativisztikus formulát az

kifejezésből kaphatjuk meg. Ennek negatív gradienséből származó erő, ha p = ℏ/r a bizonytalansági relációból:

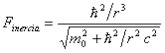
Nem-relativisztikus közelítésben a négyzetgyök alatti második tag elhanyagolható, és emiatt megkapjuk a korábbi kifejezést. A másik határesetben, ha az m₀ nyugalmi tömeg kicsi, vagy nulla, mint a foton esetében, akkor az erő kifejezése F_inercia = ℏ.c/r² éppen azonos lesz avval a vonzóerővel, amit fénysebességű forgások hoznak létre a téridő torzulása miatt (Lásd „Térgörbület és gravitáció forgó rendszerekben”). Ez megfelel annak az elképzelésnek, hogy a foton a térpontok egydimenziós fénysebességű forgása, mert a forgás stabilitását az inercia erő és az erős gravitáció egyensúlya képes biztosítani.

A tehetetlenségi erő alapján értelmezhetjük a nullaponti rezgés energiáját is. Ekkor az x változó szerepel r helyett. A tehetetlenségi és vonzóerő erőegyensúlya

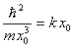: azaz 

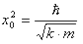
Az x₀ egyensúlyi kitérést az A amplitúdóval azonosítva megkapjuk az energiát

:

Tehát a nullponti rezgés energiája valóban visszavezethető a bizonytalansági elvből származtatott inercia erő és a vegyérték erő egyensúlyára.

A bizonytalansági elvet a részecskékről szerezhető információ korlátozottságára vezettük vissza, de jogosan vethető fel a kérdés: hogyan vezethet bármilyen erőhatáshoz az információ hiánya? Hétköznapi életünkben nagyszámú foton áradata ér el minket, ugyanez érvényes a klasszikus fizikai kísérletekben is. Az általuk szállított információban csak a fotonok átlagos tulajdonsága érvényesül és emiatt elvész az egyes fotonok individuális tulajdonsága: az egyedi fázis. Az így szerzett információt dolgozza fel agyunk és alakítja ki fogalomrendszerét, amit aztán a tudomány rendszeresít és beszél erőről, energiáról, impulzusról és így tovább. A foton áradat által megismert mozgásokat klasszikus fogalmaink jól írják le, de nehézségekbe ütközünk, amikor átlépünk egy határt. Ez a határ, amikor már az egyes fotonok hatása is szerepet játszik, amikor az ismeretlen fázis határozza meg a fizikai kísérlet kimenetelét. Amikor bizonytalanságról beszélünk a pozíció és az impulzus mérése során, akkor azt fejezzük ki, hogy klasszikus fogalmaink csak korlátozott mértékben használhatók a mikrovilág törvényeinek megalkotására. Nem tekinthetjük ezért sem az energiát, sem az erőt, vagy akár az impulzust és a térbeli pozíciót olyan fogalomnak, ami elválasztható attól az úttól, ami elvezetett a fogalmak megalkotásához.  A fotonok kvantumos jellege ezért bizonyos formában megjelenik az energia és erő fogalmában is. Ez nem jelenti azt, hogy tagadni kellene az erő, vagy az energia objektív létezését, csupán azok megjelenési formája függ attól az eszköztől, ami az információt biztosítja számunkra.

A fizika megkülönbözteti a valódi erőt, mint például a tömegek közötti vonzást, vagy az elektromos töltések közötti erőhatásokat a tehetetlenségi erőktől, mert az utóbbit a választott koordináta rendszer tulajdonságaihoz köti, ezek akkor lépnek fel, ha nem inercia rendszerről, hanem valamilyen gyorsuló mozgást végző rendszerről van szó. Az általános relativitás elmélete már lyukat ütött ezen a szétválasztáson, amikor kimondta, hogy nincs különbség aközött, hogy valamilyen nagy tömeg vonzását érezzük, vagy a rendszer gyorsul, ahol a megfigyelést végezzük. Ez az elv vezette Einsteint annak megfogalmazásához, hogy a gravitáció nem más, mint a téridő torzulása az euklideszi geometriához képest. Amikor alkalmazzuk a kvantummechanika elveit, akkor is elfogadunk egy leírási módot, aminek tengelyében a valószínűség elve van. Ez a valószínűségi elv vezet el a bizonytalansági erő fogalmához. A bizonytalansági erő ezért minőségében nem különbözik bármely más erőhatástól, hiszen minden erő attól függ, hogy milyen leírási módot használunk.

            A bizonytalansági elvből származtatott tehetetlenségi erőt értelmezhetjük a kvantumelektrodinamika fogalmaival is. A Coulomb erőt a virtuális fotonok közvetítik. Itt a fotonok széles frekvencia tartománya játszik szerepet, még pedig minél közelebb van az elektron a protonhoz, annál kisebb hullámhosszú, azaz annál nagyobb impulzusú fotonok adják a döntő járulékot. Emiatt az r távolság függvényében a kinetikus energia, amely négyzetesen arányos az impulzussal a távolság reciprokának négyzetével lesz arányos. A kinetikus energia r függéséből a gradiens képzésen keresztül kapjuk az erőhatást, amely így   r^-3 függést mutat.

A blog további bejegyzéseinek összefoglalóját lásd: "Paradigmaváltás a fizikában"