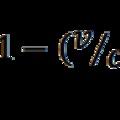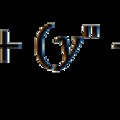Nemes Ilona:
A szakértelemig – és tovább
Korreferátum Rockenbauer Antal: A koldus és királyfi története, avagy hogyan érthetjük meg a mikrovilág titkait? c. tanulmányához.
Azért törekszünk részletes tudásra, hogy minél jobban megismerjük a nagyobb egészet, amiben élünk – és amiből élünk. Ám minél részletesebb-részletezőbb a tudásunk, annál inkább eltávolodhat a nagy egésztől. Viszont: minél inkább eltávolodunk az egésztől, annál inkább szükséges, hogy oda visszakapcsolódjunk (ld. újra: benne élünk, belőle élünk). Tehát: minél szűkebb területen tevékenykedünk, annál nagyobb szükségünk van tudásunk tágítására. Paradox helyzet ez – mondhatja erre akár a hétköznapi gondolkodás is. Ha egy helyzetet paradoxnak érzünk – mondja erre a gondolkodás műveleteit tanulmányozó gyakorlati filozófia – akkor gondolkodjunk róla adekvát módon. Paradoxonokban. Ezek, mint tudjuk, olyan „ellentmondások”, amelyek csupán látszólag feloldhatatlanok. Valójában feloldhatóak, mert egymásra tudnak vonatkoztatni térben és időben nagyon távol álló dolgokat. A szakértelem fenti paradoxona – a résztudás és az egészre vonatkozó tudás látszólagos ellentmondása eszerint szintén feloldható. A feloldás kísérlete évszázados, sőt, talán évezredes: ez a tudományok, művészetek stb. összeadására, az interdiszciplinalitásra való törekvés. Sajátos – itt nem részletezhető – módjai vannak ennek, egyikük éppen a paradoxonos gondolkodáson alapul. Eszerint a paradoxon – tágas látóköréből adódóan tágas lehetőséget ad a a szakértelemnek, hogy másokéval összekapcsolódjék. Ha tehát bármilyen szakmunka interdiszciplináris értékét szándékozunk vizsgálni, azt kell szemügyre vennünk, hogyan működteti a paradoxonokat.
Ezt kutatjuk a továbbiakban Rockenbauer Antal tanulmányában.
Már a cím „paradoxonbarát”: olyan távoli dolgokat hoz össze, mint irodalom és fizika. (A távolságot ne becsüljük le. Létezik olyan gondolkodás, amelyben a „kettő” kizáró ellentétbe, sőt, feloldhatatlan ellentmondásba rendeződik. Erre aztán iskolák épülnek, nemzedékeknek adva tovább a szétdarabolás gondolkodásmódját előidézve az iskolaparadoxont. Erről is érdemes lenne egyszer beszélni – egy más alkalommal.)
Rockenbauer Antal tanulmányában a szakterületek szétdarabolásáról szó sincs. Már az irodalmi hivatkozás sem csupán díszítőelem, hanem műveletté válik a
továbbiakban. Így: „Mark Twain regényében a gazdag környezetben felnövő királyfi állandóan konfliktusba kerül a szegények világával, amikor odakerül, mert magával hozott fogalmi rendszere ütközik a koldusokéval. Mi is hasonló helyzetben vagyunk, amikor az információbőség birodalmából látogatást teszünk az információszűkösség mikrovilágába, mert nem vagyunk képesek hátrahagyni megszokott fogalmainkat. Ez az eredete a mikrovilágról alkotott paradoxonainknak.”
Az irodalom és fizika különállásának és összetartozásának paradoxona sajátosan oldódik itt. Egyrészt úgy, hogy e két „szakterület” kölcsönösen értelmezi egymást. (Közbevetőleg ennek érzelmi katarzisértékét is becsüljük meg: a gondolkodó ilyenkor érzi, hogy nincs egyedül, mert más területek művelői is találkoznak az ő problémájával). A feloldás másik sajátosága abban nyilvánul, hogy az irodalom-fizika kapcsolat újabb paradoxont tesz láthatóvá. Az információbőség és szűkösség különbözőségének és összetartozásának paradoxona ez, amely a fizikus számára a makro- és mikrovilág különbözőségében és összetartozásában nyilvánul meg.
A lecke fel van adva a fizikatudósnak: hogyan lehet úgy – a szerző szavával – hátrahagyni makrovilágon iskolázott fogalmainkat, hogy a makro – és mikrovilágot ne daraboljuk szét (azaz: a szaktudós ne rekessze ki tartósan a valóság egy részét.) Mondanunk sem kell, ez a „hátrahagyás” paradoxona.
A szerző itt is old. Úgy hagyja hátra a makrofizika műveleteit, hogy kipróbálja őket, miközben azok működésben mutatják meg használhatóságukat – és elégtelenségüket egyszersmind.
Mire használható például a makrovilágon iskolázott gondolkodás egyik (kedvelt) művelete a számszerűség? A szerző szerint arra (is), hogy segítségével kialakulhasson egy sajátos hierarchia nagyságrendi alapon. (A tanulmányban: atom, DNS molekula, egysejtűek, ember, emberiség, óceánok, Nap, Galaxis, Univerzum).
Könnyű belátni, hogy a szerző itt is tágít. Bizonyos mértékig „ugyanúgy” ahogy a fizikát és irodalmat összekapcsolta, most a mikrovilágot helyezi el a makroban. Ezért szinte már várjuk, hogy miként ott előbújt egy paradoxon (fizika és irodalom különbözősége és összetartozása) itt is meg fog jelenni egy sajátos változat. Meg is jelenik: ez a műveletátvitel paradoxona. A szerző ezt a következőképpen vezeti be: „ A lego nevű kirakós játékban az egyes elemek ismerete nem határozza meg a belőlük összerakható tárgyakat, ehhez kell egy „terv” vagy „minta”, amely megadja az egyes tárgyak összekapcsolási struktúráját, így a fizika hiába ismeri az atomok összekapcsolási szabályait, ebből még nem juthatunk el az élet törvényeihez”.
Eszerint tehát egy bizonyos szakterület műveletei (példánkban a számszerűségé) szükségesek lehetnek ugyan minden más területen, de nem fedik le, különösen pedig nem oldják meg azok sajátszerű problémáit. (A műveletek csereberéjére, sőt, egyeduralmi törekvésére változatos példák vannak a gondolkodás történetében. Ezekre most nem térhetünk ki, ám tartsuk evidenciában.)
A műveletátvitel paradoxona végigkíséri az egész tanulmányt, miközben különböző módokon oldódik – és újabb paradoxonokkal gazdagodik.
Első lépésben fizikatörténeti áttekintés oldja a műveletátvitel paradoxonát. Egymásra rétegződik ebben Newton mozgástörvénye, a Bohr-féle atommodell és átalakulása a kvantummechanikáig vezető úton egészen a fotonok „mozgástörvényeiig.”
A tanulmánynak ebben a részében találkozik a szerző (és értő olvasója) a történetiség paradoxonával: a kronologikus „leltár” szükségességével és egyben elégtelenségével. A tanulmányban ez is oldódik. Következőképpen: a szerző hangsúlyozottan figyel az egyes fizikatörténeti „vívmányok” egymásból és egymásba alakulására. (Látványos nyelvi nyomai is vannak ennek, ehhez elég csak az alcímeket követnünk: Az atom fogalma is átalakul. A makrovilág fogalmainak átalakulása a kvantummechanikában. A kvantum eredete és az impulzusnyomaték átalakulása, A tér fogalmának átalakulása stb.)
És itt az újabb paradoxon: az átalakulásé. Hogy működik? Ehhez össze kell (és lehet) hoznunk a szerző korábban már idézett két gondolatát. Az egyik: >> kell egy „terv” vagy „minta”, amely megadja az egyes tárgyak összekapcsolásának struktúráját.<< A másik: „nem vagyunk képesek hátrahagyni (a mikrovilágban sem) megszokott fogalmainkat. Ez az eredete mikrovilágról alkotott paradoxonainknak”. Lefordítva az átalakuláséra: kell egy külső mozgató az átalakuláshoz, ám ez magába rejti a megszokotthoz való ragaszkodást, – és ezzel maga válik a változás gátjává.
Feloldódik-e ez a paradoxon (is) a tanulmányban? Mint sejthetjük igen, méghozzá összefoglaló módon: „Összegezve megállapíthatjuk, hogy a forgás makroszkopikus fogalmát érdemes kiterjeszteni a részecskék világára is, mert bár erről a forgásról nincs közvetlen információnk, viszont újszerű összefüggéseket nyerhetünk a részecskék alapvető tulajdonságai között. A forgás időbeli lefutását nem tudjuk nyomon követni, ezért itt is a kvantummechanika valószínűségi elvét kell alapul venni, azaz a forgást nem a klasszikus pályafüggvény írja le, hanem az állapotfüggvény, amelyben az S = 1 spin a fotonoknál és a gyenge kölcsönhatás bozonjainál. Elektronok esetén ezt a kiterjesztést Dirac relativisztikus egyenlete
oldja meg. A fénysebességű forgásnál az idő dimenzióját a valószínűség dimenziója helyettesíti.
Az idézett szövegrészben (valamint a tanulmány egészében) a makrofizka fogalmai és műveletei úgy működnek együtt a mikrofizika fogalmaival és műveleteivel, hogy segítségükkel újszerű összefüggés fogalmazható meg a részecskék alapvető tulajdonságai között. Új értelmet nyer a mikrovilágban a forgás, a valószínűség és az idő.
Így oldódik tehát az átalakulás paradoxona a mikrovilágban. A külső minták (a makrovilág fogalmai és műveletei – ld. újra az idézetet és a tanulmány egészét) előhívják a mikrovilág összefüggéseit, miközben maguk is átalakulnak.
Vajon előhívnak-e újabb paradoxont is? Például a valószínűségét. Természetesen. Ez már a hétköznapi gondolkodás számára látható: valószínű az, ami létezik is meg nem is. A tanulmány természetesen nem éri be a hétköznapi fogalommal. Sőt, a szaktudományossal sem: miközben a valószínűség makro és mikrofizikai fogalmait működteti, rányitja a szaktudományos gondolkodást a legtágasabb összefüggésre: az idődimenzióra.
(Emlékezzünk: a fénysebességű forgásnál az idő dimenzióját a valószínűség dimenziója helyettesíti).
Ha a valószínűség dimenziója és az időé „csereszabatos”, akkor az előbbi paradoxonát az utóbbi is feloldhatja. Ám hogyan működik ebből a szempontból az idő? Lépjünk ki a tanulmány által egyszer már járt útra, és a szemlélhetőséghez hívjuk segítségül újra az irodalmat. Ezúttal József Attilát és az Eszméletet: „Csak ami nincs, annak van bokra,\ csak ami lesz, az a virág,\ Ami van széthull darabokra.” Ebben a szellemben folytathatjuk is a természeti képet akár tapasztalati alapon (magától értetődik: hétköznapi nyelven és prózában): Ami darabokban van, az új dologgá ismét összeállhat, hogy aztán ismét széthulljon új változatokat kínálva. Az idő eszerint úgy oldja fel a paradox dolgokat, helyzeteket, hogy más alakban újrateremti őket. Működteti a változás paradoxonát. Ez nyilvánul meg a fizikában többek között a valószínűségben, irodalomban a képszerűségben, sőt feltételezhetjük, hogy mindenfajta más tevékenységben sajátszerű módon. Folytatva a feltételezést: lehetséges (ám itt és most nem bizonyítható) hogy minden tudományok és művészetek közös nevezője a bennük rejlő paradoxon. Ennek alapján csatlakoztatni lehet őket egymáshoz és az időfolyamathoz. Azaz: ilymódon lehetséges egy időalapú interdiszciplinaritás.
Rockenbauer Antal tanulmánya szerint ehhez kapcsolható a fizika is: a valószínűségen és a feltárt paradoxonokon keresztül.
(A feltárást ebben az esetben a gyakorlati filozófia gondolkodástechnikai ágának műveleteivel végeztük.)