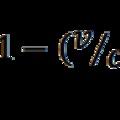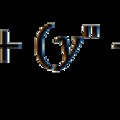Amikor egy tudományágban bizonyos törvények általánosan elfogadottá válnak rendkívül nehéz olyan eredményt elfogadtatni, amely azt részben, vagy egészben cáfolná. Sokkal könnyebb olyan közleményeket elhelyezni a szakirodalomban, amely nem ad igazán újat, hanem a jól bevált és elfogadott nyomon halad, csak azért legyen valami új is benne, akár a vizsgált anyag, akár a módszertan tekintetében. Ennek felel meg saját publikációm többsége is, melyeket részben a legnagyobb tekintélyű fizikai és kémiai folyóiratokban sikerült közölni. Most azonban belefutottam én is a fönt említett korlátba, amikor olyan eredményre jutottam, amely már sérthetett bizonyos tekintélyeket.
Van-e tömege a neutrínóknak?
Miről is volt szó? A részecskefizikának van két erősen vitatható állítása, amit a fizika irányadó kutatói mégis elfogadnak. Az egyik, hogy van-e a neutrínónak nyugalmi tömege. Az első megfigyelések szerint a neutrínó fénysebességgel halad, ezért a részecskék tulajdonságait összegző Standard Modell szerint nincs is nyugalmi tömege. A későbbi vizsgálatok azonban világossá tették, hogy a neutrínónak három különböző típusa van, amit elektron, müon és tau neutrínónak neveznek. Ezek a részecskék minden tulajdonságban egyeznek, a spinjük ½, töltésük nulla, így csak abban térhetnek el, ha mégiscsak van tömegük. Ezt a különbséget az bizonyítja, hogy ezek a részecskék a képződésük után átalakulnak egymásba, amit neutrínó oszcillációnak neveznek. Erről már több alkalommal is írtam a blogban, legutóbb „A neutrínó kalandos története” című írásban. Végül is hogyan lehet eldönteni, hogy van, vagy nincs tömege a neutrínónak? Ebben segít a pontos sebességmérés, mert ha létezik nyugalmi tömeg, akkor a relativitáselmélet tömegnövekedési törvénye szerint a részecske sebessége nem érheti el a c értéket, azaz a fény sebességét vákuumban. Több mérést is végeztek különböző laboratóriumban, de a mérési határon belül mindig azt kapták, hogy a sebesség megegyezik c-vel. Sőt egyszer még az a hír is lábra kapott, hogy c-nél nagyobb a sebesség, de aztán ezt visszavonták, mert a mérés során technikai hibát követtek el. Tehát jelenleg ott tartunk, hogy az eddigi sebességmérések szerint a neutrínó nullatömegű részecske. Van azonban egy kibúvó, hiszen minden mérésnek van hibahatára, ezért nem cáfolható meg, hogy ezen belül mégiscsak kicsit lassabb lenne a neutrínó sebessége c-nél, amiből pedig megbecsülhetjük a tömeg lehetséges felső határát. A mérések fokozódó pontossága mellett most ott tartunk, hogy a neutrínó tömege, legalább is az elektron típusúé, nem lehet nagyobb, mint a parányi elektron tömegének milliomod része. Valljuk be, ez bizony elég gyöngécske magyarázat, de ha a jövőben még pontosabb sebességmérést végeznek, akkor is megmarad a kibúvó, hiszen a mérés akkor sem lesz végtelenül pontos. Nem lenne hát célszerű megnézni, hogy nincs-e olyan elmélet, amelyik magyarázná a neutrínó oszcillációt akkor is, ha a nyugalmi tömeg nulla? Már tettem is egy ilyen javaslatot, amely a „Hogyan oszcillálnak a nulla nyugalmi tömegű neutrínók” írásban olvasható.
Miért nem lehet megfigyelni a kvarkokat?
Mielőtt erre rátérnék, nézzük a másik széles körben elfogadott, de mégis vitatható hipotézist. Ez a kvarkokra, a törttöltésű elemi részecskékre vonatkozik. Addig, amíg csak az atomot felépítő elektront, protont és neutront ismertük tisztának látszott a kép. Bonyolódott a helyzet a pozitron felfedezésével, de ennek még örültünk, mert magyarázatot adott Dirac nagyszerű felfedezésének egy vitatott kérdésére, amikor megalkotta relativisztikus hullámegyenletét, amely negatív energiájú megoldásokra is vezetett. Ez lett az alapja a lyukelméletnek, amely ugyan később nem állta meg a helyét, de most nem evvel akarunk foglalkozni. Az pozitron felfedezésével csaknem egy időben került sor az első neutrínó kimutatására. Ezekre akkortájt még Nobel-díjakat is adtak. De aztán egyre-másra találtak új és újabb elemi részecskét, amire nem volt magyarázat. Ezeket két nagy csoportba lehetett osztani a spinük szerint, a félegész spinüek a barionok, az egész spinűek a mezonok. Ezek száma ma már jóval száz fölött van. De megszületett a nagyszerű elmélet, amikor két alap kvarkkal , a +2/3e töltésű up és -1/3e töltésű down kvarkból és ezek magasabb generációival és antirészecske párjukkal valamennyi bariont és mezont fel lehetett építeni. Lásd például a „Kvark színe” című írást a blogban. Bár meghökkentő volt a feltevés, hogy létezhetnek törttöltésű elemi objektumok is, de olyan jól lehetett evvel valamennyi most már összetettnek tekinthető részecskét értelmezni, ami eloszlatta a kételyeket. Ezután már természetes volt, hogy az elmélet alkotói megérdemelten nyerték el a Nobel-díjat. De itt is van egy bökkenő: ilyen törttöltésű részecskét sehogyan sem lehetett megfigyelni (lásd: „Miért nem lehet szabad kvarkokat megfigyelni". Ez fel is vetette a kérdést, vajon csak egy kitűnő rendezési elvről van szó, vagy tényleg léteznek a kvarkok, mint valódi részecskék, csak a jelenlegi kísérleti körülmények között nem tudjuk detektálni ezeket. Jött is egy magyarázat, amit „bezártsági elvnek” (confinement) neveznek, amely azt mondja ki, hogy olyan nagy erővel kapaszkodnak össze a barionokban és mezonokban a kvarkok, hogy nincs elég nagy erő, ami a kötéseket felhasítaná. Evvel az elvvel is gond van, mert a nukleonok (proton és neutron) energiáját több mint százszor meghaladó ütközési kísérletekben, ahol mindig óriási számú részecske jön létre, nem lehetett látni törttöltésű objektumokat. Hasonló a helyzet a kozmikus sugárzásban, ahol még ennél jóval nagyobb energiájú részecskék is érkeznek. Mit jelent ez? Azt, hogy a kötési energia a bezártsági elv szerint nagyságrenddel kellene meghaladja bármely megfigyelt elemi objektumét beleértve a kvarkoknak tulajdonított renormált tömeget is. Itt is felvetődik a kérdés, hogy nem kellene olyan elméleten gondolkozni, amelyik természetes módon magyarázná a kvarkok megfigyelhetetlenségét? (Lásd: „Miért nem lehet szabad kvarkokat megfigyelni?”)
Egy új elmélet születése
Az ilyen elméletek általában nem úgy születnek, hogy valaki elhatározza ennek kidolgozását, hanem ha teljesen máshonnan indul el és szinte véletlenül jut el a felismeréshez. Ez történt velem is. Érdekelt a dolog, hogy Dirac relativisztikus hullámegyenlete nem terjeszthető-e ki a többi elemi részecskére a törttöltésű kvarkokra és a töltés nélküli neutrínókra. Megpróbáltam Dirac eredeti gondolatából kiindulni, mégpedig az energia relativisztikus kovariancia kifejezéséből (ez egy négyzetes összefüggés az energia különböző összetevői között, lásd pl. „Még egyszer a Dirac egyenletről” és „A Dirac egyenlettől az általános fermion egyenletig”). Dirac zseniális ötlete volt, hogy a négyzetgyökvonást négy lineáris egyenletre bontotta fel négydimenziós mátrixok (spinorok) segítségével. Ennek a felbontásnak köszönhetjük a spin fogalmának megszületését, ami az elemi részecskék legalapvetőbb tulajdonsága, hiszen még a töltéssel és tömeggel nem rendelkező részecskék is rendelkeznek spinnel. A másik következmény az energia előjelének kétértékűsége lett. A spin és az energia két előjelének fellépése arra vezethető vissza, hogy a kovariancia formulában négyzetes kifejezések vannak, és így a pozitív és negatív értékek egyaránt kielégítik az összefüggést. Ez az összefüggés azonban egy harmadik kettősséget is rejteget, ezért számomra indokoltnak tűnt, hogy kibővítsen Dirac ötletét és a felbontást nyolcdimenziós spinorokkal végezzem el. Ez úgy volt lehetséges, ha a tömeg és töltés fogalmát általánosítom, amely ettől fogva nem egy szimpla konstans volt, hanem egy kétdimenziós mátrix, ami kifejezhető a Pauli mátrixok segítségével. Ezáltal a tömeg és töltés hasonló tulajdonságot vett fel, mint a spin. A kvantummechanikában a fizikai mennyiségeket, az energiát, impulzust és impulzusmomentumot operátorok alkotják, viszont azáltal, hogy a tömeget és töltést is mátrixok, azaz operátorok képviselik, egy olyan formalizmushoz jutunk, amelyben már minden egyes fizikai mennyiség operátor lett. Ily módon egy teljes, konzekvens kvantummechanikához lehetett jutni. Ebben a formalizmusban már közös alapra lehetett helyezni a Standard Modell összes valóban eleminek tekintett fermionját: az elektron-pozitron párt, a neutrínót és a kvarkokat is, amelyeket egyetlen új kvantumszám különböztet meg. Ebben a töltést és a tömeget a megfelelő operátorok várhatóértéke képviseli, amit az általánosított Dirac egyenlet – amit fermion egyenletnek neveztem el – határoz meg.
Az új egyenlet meglepő következményei
A meglepetés akkor ért, amikor az új egyenlet következményeit vizsgáltam a neutrínók és a kvarkok esetén. A neutrínóknál a tömeg és töltés várhatóértéke nulla, a relativisztikus sebességfüggés ezt a várható értéket növeli meg a tömeg esetében. De ha ez nulla, akkor nincs akadálya, hogy a neutrínó fénysebességgel haladjon. Ugyanakkor a tömeg spinor jellege avval jár, hogy a nem-diagonális elemek nem lesznek nullák és így különbséget tehetünk a háromféle neutrínó között. Tehát választ kapunk arra is, hogyan oszcillálhat egymás között a három neutrínó típus.
De mi a helyzet a kvarkokkal? A kvarkok törttöltése is mint várhatóérték adódik ki, amely azonban különbözik a töltés operátor sajátértékétől, ami csak +e és –e lehet. De mit mond ki a kvantummechanika? A mikro-objektum állapotát a hullámfüggvény határozza meg, amely bizonyos fizikai mennyiségek számára több lehetséges értéket tesz lehetővé, megadva azok valószínűségét is. A neutrínót úgy foghatjuk fel, mint a részecske olyan kvantummechanikai állapotát, ahol a két sajátérték valószínűsége megegyezik és így a várhatóérték nulla lesz. Kvarkoknál pedig azért alakul ki törttöltés, mert a +e és –e töltésállapotok súlya eltérő lesz. De ha végrehajtjuk a mérést, akkor csupán a sajátértékek egyike valósulhat meg. Ezt hívja a szakirodalom a hullámfüggvény redukciójának. Ez azt jelenti, hogy a részecskék detektálása során kizárólag olyan részecskét láthatunk, ahol vagy –e, vagy +e a töltés. Más szóval a törttöltésű kvark egy mérés előtti kvantummechanikai állapot, és nem ténylegesen detektálható részecske. Ily módon a kvantummechanika alapelve világos választ ad arra, hogy a kvarkok miért nem figyelhetők meg.
Kísérlet az eredmények publikálására
Ha viszont két ilyen alapvető és sokszorosan alátámasztott kísérleti tényre jó választ ad az elmélet, akkor joggal bízhatunk az elmélet helyességében. Ez a részecskefizika szempontjából rendkívül fontos eredmény. Ilyenkor a kutatóban felébred a kétely: lehet, hogy valahol hibádzik az elgondolása, hiba lehet a logikában, vagy a matematikai eljárásban? Ennek legjobb próbája, ha a tudományterület legjobb kutatói ellenőrzik az elmélet és a következtetések helyességét. Erre sor kerül, mielőtt az eredmény publikálásra kerül. Ez a vizsgálat különösen szigorú a legjelentősebb folyóiratoknál. Erre a célra a fizika legtekintélyesebb folyóiratát (Physical Review Letters, PRL) választottam, már csak azért is, mert ebben a folyóiratban is jelentek meg korábban közleményeim. A benyújtás után először a szerkesztőség foglal állást, hogy érdemesnek tartja-e a munkát publikálásra, és ha igen, akkor kiküldi szakmai bírálatra. Az én publikációm nem jutott el erre a második fázisra, de nem azért, mert szakmai hibát találtak volna benne, hanem mert az eredményeket nem tartották elég jelentősnek ahhoz, hogy a PRL közölje. Arra hivatkoztak, hogy az újabban tovább emelt fontossági kritériumoknak nem felel meg az írás, szakmailag viszont nem kritizálták, sőt javasolták, hogy küldjem el a kéziratot egy erre specializált folyóiratnak. Én az elutasítást nem fogadtam el, mert az eredmények alapvető fontosságúnak tartom a részecskefizika továbbfejlődése érdekében. Ezt megírtam a szerkesztőnek, aki tett egy korrekt javaslatot – érdemes ezért a nevét is megemlíteni: Dr. Stojan Rebic – aki javasolta, nyújtsak be fellebbezést a „Divisional Associate Editor” (DAE) testületéhez. A fellebbezést be is nyújtottam, amelyben rámutattam, hogy tévedés történt az előzetes elbírálás során, mert az eredmények jelentősége egyértelműen bizonyítja, hogy a kéziratnak a PRL-nél van a helye. Kértem ezért, hogy küldjék ki a kéziratot szakmai bírálatra. Hosszú ideig nem jött válasz, majd kétszeri sürgetés után csaknem két hónap elteltével jött az újabb elutasítás. De ismét szó sem volt szakmai kifogásról, ezúttal nem tértek ki arra sem, hogy ne lenne igazán fontos az eredmény. Mit is írt a bírálatot elkészítő DAE szerkesztő? Indulásként megjegyezte, hogy ő miben hisz: egyrészt abban, hogy a neutrínók lassabban mozognak mint a fény, másrészt abban, hogy a kvarkok bezártságát az erős kölcsönhatás okozza. Más szóval azt fejtette ki, hogy ő a mai elfogadott részecskefizikai koncepciókban hisz. A következő mondatban viszont elismerte, hogy nem tudja megítélni a beküldött kézirat szakmai helyességét és javasolja a kézirat speciális folyóirathoz küldését. Ez a vélemény annyira meghökkentő egy tekintélyes szerkesztőség tekintélyes tagjától, hogy érdemes az eredeti angol szöveget itt változtatás nélkül leírni:
The author proposes a generalization of the Dirac equation that leads to the possibility of neutrinos traveling at the speed of light and explains quark confinement. I believe the neutrinos don't travel at the speed of light due to their non-zero mass and quark confinement has to do with properties of the strong interaction. Since my confusion may be due to some technicality that I don't understand properly I would suggest the author to send his work to a more specialized journal, where his work could be better appreciated.
- E.M. Wagner
Divisional Associate Editor
Physical Review Letters
A közlés elutasításának oka
Az alsóbb szintű szerkesztőség erre a véleményre alapozva utasította el végül a kéziratot. Tehát fontosabb, hogy mit hisz az önmagát inkompetensnek nevező bíráló, mint bármely tudományos szakmai érv? Néhány századdal a Galilei-per után is kísért még az inkvizíció szelleme?
Az elutasítás valódi okát csak sejthetem. A nagy tekintélyű tudósok véleményével szemben hogyan jelentethetnének meg egy közleményt, amely avval szembemegy? Itt tart hát a fizikai véleményalkotás szabadsága napjainkban!
A blog további írásai a megfelelő linkekkel megtalálható a „Paradigmaváltás a fizikában” című bejegyzésben.