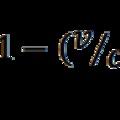Kaptam egy levelet az egyik olvasótól, amit itt idézek a név kezdő betűjét feltüntetve, mert a megjegyzés nem mint nyilvános komment érkezett:
Tisztelt R. A. !
Olvastam „Az ikerparadoxon: a látszat valósága” blog bejegyzést. Igaz, hogy másutt is olvastam már többször erről a problémáról. A leírásokban mindenütt megjelenik az idő dilatáció kérdése. Ami együtt jár azzal, hogy idő múlása változhat. Vagyis nagy sebességű mozgások esetén az idő lelassul, a levezetések és magyarázatok alapján. És ennek megfelelően az órák lassabban járnak. A változások mértékét a relativitáselmélet Lorentz-kontrakciós szabálya szerint számolják ki. Amit két óra eltérésének összevetésével igazolnak. /Hafele-Keating kísérlet/ Az idő dilatáció még a gravitációs mezővel is kapcsolatban van. Erős gravitációs erőtérben az idő szintén lelassul a ma elfogadott álláspont szerint.
Egyetlen egy dologról nem esik szó sehol, az idő múlásának méréséről. Minden esetben természetesnek tekintik, hogy az idő mérhető, és mi ezt az óráinkkal mérni tudjuk.
Vizsgáljuk meg az óráinkat, vagyis mérőeszközeinket az időméréssel kapcsolatban.
Segítségképpen először vizsgáljuk meg, hogy mérjük a különböző fizikai mennyiségeket. Nézzük a legalapvetőbbeket. A tömeget, az elektromos áramot, a hőmérsékletet. A tömeg mérése erőmérésre vezethető vissza, ha a tömeg változik, akkor a mérlegre ható erő is változik. Az elektromos áram változása szintén mérhető az erőhatás változásával, de mérhető anyag kiválasztással is. A hőmérséklet változása akár térfogat változással, nyomásváltozással is mérhető, de még színváltozással is. Vagyis azt mondhatjuk, hogy valamilyen fizikai mennyiség vagy változásának mérése, mindig valamilyen, az általa kiváltott valamilyen másik fizikai mennyiséggel, vagy annak változással mérhető. Ami valamilyen mérőeszközre hatással van. Azonban az idő múlása, vagy esetleg múlásának sebesség változása környezetünkben nem köthető semmilyen fizikailag érzékelhető változáshoz. Nincs ilyen ismert tulajdonsága.
Ezek után vizsgáljuk meg az időmérő eszközeinket.
A napórát, az ingaórát, az atomórát.
Kezdjük a legősibb legegyszerűbb eszközzel a napórával. A napóra mutatójának árnyéka azért mozog, mert múlik az idő vagy azért, mert a Föld forog és kering a Nap körül. Elég egyértelmű választ lehet adni. Ezt bizony a Föld forgása és keringése miatt van. A Föld forgására nincs befolyással az idő múlása vagy annak változás. Tehát az idő múlása nem befolyásolja a Napórát. Itt viszont ellentmondás van a tudomány mai állása és a napóra között. Ha ugyanis nőne a Föld forgási vagy keringési sebessége napóra árnyéka gyorsabban mozogna, vagyis az általa mért idő gyorsabb lenne. Az Einsteini elmélet szerint a nagy sebességű mozgás esetén az idő lelassul. A napóra nem így viselkedik.
Nézzük az ingaórát, és a matematikai ingát mivel ez az ingaóra alapja. A matematikai inga lengésideje.
T=2π√(L/g) Nézzük meg a képletet! Látjuk, hogy az inga hosszának /L/ a változása, vagy a gravitáció /g/ megváltozása esetén, megváltozik az inga lengésideje. Azt tudjuk, hogy az inga hosszára az idő nincs semmilyen hatással. Marad a gravitáció változása, ami változik is a környezetünkben. A gravitáció változása a képlet alapján módosítja az ingalengés idejét. Ez viszont azt jelenti, hogy az időnek befolyással kellene lenni az gravitációra, ha így időt akarunk mérni. Azonban ma nincs bizonyíték arra, hogy az idő bármilyen befolyással lenne a gravitációra, vagy lenne olyan tulajdonsága, ami a gravitációt bármilyen módon is befolyásolni tudná. Ha az idő múlása befolyásolná a gravitációt, akkor annak folyamatosan változnia kellene, de ez nem így van. Ez viszont így azt jelenti, hogy az ingaórával mi nem tudunk időt mérni. Ezzel így mi a gravitáció intenzitását tudjuk, mérni és a gravitációval arányos ütem jeleket tudunk előállítani.
Akkor nézzük az ellenkezőjét, hogy a gravitáció van befolyással az időre. Erre van tudományos álláspont. A tudomány mai álláspontja szerint az erős gravitációs erőtérben az idő lelassul. Azonban a képlet alapján az ingaóra ennek pont ellent mond. Ha nő gravitációs térerő /g/, a képlet alapján az inga lengésideje csökken, vagyis az óra siet, az idő gyorsabban múlik. Tehát ez sem felel meg a ma elfogadott álláspontnak. De akkor mit mérünk? A valós időt biztosan nem, mert az nincs semmilyen befolyással az ingára vagy a gravitációra. Ezek után azt kell feltételeznünk, amit mi az időmérésére kitaláltunk az valójában egy általunk létre hozott virtuális vagy saját idő, de ennek semmi köze nincs a valóságos időhöz. Ami vagy van, vagy nincs. Ami a legfontosabb, az általunk vizsgált ingaóra, vagy matematikai ingára semmilyen befolyással nincs a valós idő vagy annak változása. A mi időmérésünk csak egy segédeszköz a számításainkhoz, az életünkhöz. Így az ingaóra sem tudja érzékelni sem a valós idő, sem a virtuális idő változását. Tehát az idő gyorsulását, sem lassulását nem érzékeli az ingaóra sem.
Ezek után nézzük meg a nagy pontosságú atomórát. Ma ez a legpontosabbnak mondott időmérő eszköz. Jelenleg atomórát csak a Földön és földi környezetben tudunk előállítani. Az atomórának sincs egyetlen olyan alkatrésze sem, amire az idő befolyással lenne és ezt tervezésnél figyelembe vennék. A földi gravitációs erőtérben legyártott és üzembe állított atomórától mért várjuk el, hogy pontosan úgy viselkedjen, más fizikailag megváltozott körülmények közt is, mintha nem változott volna semmi a környezetében. Elég, ha a Földön más és más magasságban üzemeltetjük. Ha a gravitációs erőtérben az atomórát magasabb helyen üzemeltetjük, már a földön is kimutatható, hogy az óra sietni kezd. A kérdés itt is az, hogy ezt nagy pontosságú mérőeszközt miként tudja befolyásolnia a mérni kívánt mennyiség, az idő. Mert továbbra sem tudunk bármilyen fizikai mennyiség változásáról, amit az idő gyorsulása vagy lassulása idézne elő a Földön és ezt mérni is tudnánk vagy befolyásolni tudná az atomórát. Jelen esetben is, ami a körülményekben változik az nem más, mint a gravitációs erőtér nagysága. Ez ellen még semmilyen árnyékolást nem ismerünk. Jelenlegi ismereteink szerint a gravitáció és változása nem függ az idő múlásától. Összefoglalva a mi időmérő eszközeink nem mások, mint jeladók. Akár a mechanikus akár az atomórákról beszélünk. Ezekkel mi nem időt mérünk, hanem saját részünkre egy virtuális idő állítunk elő. Tehát arról beszélni, hogy az időmérő eszközeink érzékelik az időmúlását, vagy lassulását és gyorsulását igen erősen kétséges. Nem tudunk olyan alkatrészről sem a mechanikus órában sem az atomórában amire az idő bármilyen befolyással lenne. Helyezzünk egymás mellé egy ingaórát és egy atomórát. Vajon, hogy tudja az idő a két időmérő eszközt úgy befolyásolni, hogy egymásnak ellentmondóan mérjenek. Az egyik siessen, ha nő a gravitációs erőtér, míg a másik késsen, egymás közelében. Ezért nagyon aktuálisak az alábbi kérdések.
- kérdés: vajon tudjuk-e az időt mérni?
- kérdés: mért van ellentmondás a tudomány mai állítása, hogy erős gravitációs térben az idő lelassul, míg a napóra, az ingaóra vagy matematikai inga szerint éppen az ellenkezője történik?
III. kérdés: vajon létezik-e az idő, vagy csak egy számítási segédeszköz?
- kérdés: honnan tudja az időmérő eszköz, hogy megváltozott az idő múlásának sebessége, ha az időnek nincs olyan ismert tulajdonsága, ami hatna rá?
- Mit jelent a fizikában, ha a mi időmérésünk nem az időt méri, csak jeleket ad, vagy események sorát állítja elő?
Tisztelettel F. J.!
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Válaszomat egy előrehozott állítással kezdem: Nincs értelme egy inercia rendszeren belüli idő dilatációról, tömegnövekedésről vagy a hosszúság Lorentz kontrakciójáról beszélni, ezek a szabályok csak akkor játszanak szerepet, ha két inercia rendszert összehasonlítunk és az egyikben megállapított mértékrendszer alapján írjuk le a másik rendszerben a mozgásokat. Ez természetesen vonatkozik az idő mérésére is.
A levél első bekezdése pontosan foglalja össze a relativitáselmélet néhány szabályát, amit magam is leírtam az egyes bejegyzésekben. De térjünk rá az időmérés kérdésére. Mint a fizikában bármely területen az időmérés alapja is összehasonlítás. Kiindulhatunk bármilyen periodikus mozgásból (a Föld körforgása, inga lengése, kristályok rezgése, vagy valamilyen atom által kibocsátott fénysugár periódus ideje, és ezek alapján definiálunk egy időegységet, például a másodpercet, és erre vonatkoztatjuk az egyes mozgások, átalakulások idejét. A lényeg, hogy mindig arányokról van szó, és az összehasonlítás alapja (például a másodperc) egy megadott inercia rendszerre vonatkozik, amelyben ráadásul a gravitációs mezőt (a szabadesés gyorsulását) is állandónak vesszük. Ezt vették figyelembe a Hafele-Keating kísérletben is, amikor a magukkal vitt atomóra által mért időt (ennek másodperc egysége a sebességtől és a repülés magasságától függött), a földön letétbe helyezett másik atomórával hasonlították össze.
Az időmérésre adott példák közül nézzük a napóra és a Föld forgása közötti kapcsolatot. Szemléltessük a dolgot egy űrutazással, amikor elhagyjuk a Naprendszert, miközben felgyorsítjuk az űrhajót akkora sebességre, amelyik Lorentz kontrakciója eléri például a 90%-ot. Ha egyenletes a sebesség, mit veszünk észre ebből az űrhajóban? Semmit! Nem észleljük a tömeg növekedését, nem vesszük észre, hogy lassabban ketyegne az óra, vagy bármi rövidebb lenne. Ott belül minden a szokásos, mert ha minden arányosan változik, akkor semmi eltérés nem vehető észre. Pillantsunk azonban vissza a Földre. Ha figyeljük a Föld megfordulási idejét (lásd napóra), akkor az űrhajó órája szerint az derül ki, hogy a nap hossza csupán 2,4 óra lesz. Ha ebben a lerövidült napban határozzuk meg a Föld keringési idejét, az megmarad 365-nek, de ha az űrhajó napjaiban számolunk ez csak 36,5-nak adódik. Ha a Földről leadott jelek időbeli távolságát az űrhajón mérjük, akkor ezt az időt is hosszabbnak vesszük, mint amit a Földön mérnek.
A levél megállapítása szerint nagyobb g-nél – ellentétesen a relativitáselmélettel – az inga lengésideje nem hosszabb lesz, hanem rövidül az L/g négyzetgyökével arányos képlet szerint. Ez az újabb tévedés az általános relativitáselmélet félreértéséből adódik! Az erős tömegvonzás, amit a helyi g reprezentál, nem csak az időt változtatja meg, hanem a tér geometriáját is. Ezt írja le a formalizmus négydimenziós metrikus tenzora. Az inga esetén ez az „L” hosszúságot úgy változtatja meg, hogy emiatt a lengési idő megnövekszik, mert ez túlkompenzálja g növekedését. Egyébként sem arról van szó, hogy az idő befolyással lenne a gravitációra, hanem fordítva: az idő egységének (másodperc) hossza függ a gravitációtól!
Valóságos és virtuális idő? A kérdést nem így vetném fel! A lényeg, hogy az idő egységének megválasztása tőlünk függ. Egy vonatkoztatási (inercia) rendszeren belül – ismételve a kezdeti megállapítást – nincs értelme idő dilatációról beszélni. Ennek csak akkor van értelme, ha különböző inercia rendszereket, illetve eltérő gravitációs rendszereket hasonlítunk össze egymással.
A levél végén lévő öt pontra a fentiek megadják a választ, ezekre külön nem térek ki.
Köszönöm az észrevételt, mert alkalmat ad rá, hogy rámutassak néhány közkeletű tévedésre a relativitáselmélettel kapcsolatban.
A blog további írásait lásd: Paradigmaváltás a fizikában
- A.