Az elektron mágneses momentumát azért tekintik anomálisnak, mert a Dirac egyenlet alapján képzett momentum aránya a spinhez kétszerese a pályamozgás esetén tapasztalt értéknek. Ennek a kettes faktornak az értelmezése a klasszikus elektrodinamika szabályai alapján nem lehetséges (lásd például R.P. Feynman, R.B. Leighton, M. Sands: „Mai fizika’, Műszaki Könyvkiadó, Budapest, 1970) .
Köráramok mágneses momentuma az elektrodinamika szerint arányos az áramerősség és a terület szorzatával, ezért ha q töltés ω frekvenciával forog az r sugarú körön, akkor a momentum q.ω.r2 kifejezéssel arányos, míg az m tömeghez tartozó impulzusmomentum m.ω.r2 lesz Bármilyen forgó objektumot felbonthatunk elemi körforgásokra, ezért függetlenül a geometriától, ha a tömeg és töltés térbeli eloszlása megegyezik azonos arány várható a pályamozgástól és a spintől, amennyiben a spint is valamilyen töltéssel és tömeggel rendelkező objektum forgásával értelmezzük. Bár a Dirac egyenletből származtatott kétszeres mágneseses momentum jó közelítésben megegyezik a kísérletileg mért értékkel, de az arány ennél kismértékben nagyobb. Ennek a korrekciónak a magyarázatára vállalkozott a kvantumelektrodinamika (QED).
Az elektron mágneses momentumának értelmezése végül is a QED igazi sikertörténete lett. Ahogy a kísérleti pontosság határát sikerült egyre több tizedes jegyre kiterjeszteni, avval lépést tartott az elmélet, amikor a QED perturbációs formalizmusában egyre magasabb rendű közelítéseket alkalmaztak (Lásd R.P. Feynman „QED, The strange theory of light and matter”, Penguin books, Princeton University Press, 1985 ). Nem tekinthetjük célunknak, hogy ekkora pontossággal értelmezzük a mágneses momentumot a részecskék fénysebességű forgásmodelljével, de bemutatjuk, hogy ennek segítségével feloldhatjuk az anomáliát és becslést adhatunk még a legfontosabb korrekciós tagra is.
A μ mágneses momentum adja meg az elektron energiaváltozását B mágneses mezőben: E = –μ.B. Amikor mágneses térről beszélünk voltaképp igen nagyszámú kollektív körforgást végző elektron hatásáról van szó, amelyik megváltoztatja egy kiszemelt elektron energiáját. Természetesen a kiválasztott elektron is hat az említett elektron rendszerre, de ez a hatás elhanyagolható a teret felépítő elektronok nagy száma miatt. A Zeeman által felfedezett kölcsönhatás energia operátorát a relativisztikus Dirac egyenletből lehet származtatni. A kölcsönhatás két tagból áll: az elektron atommag körüli pályamozgásából, amit az L.ħ pálya momentum jellemez (lásd „Miért diszkrétek az energianívók kötött állapotban” bejegyzést) és az elektron saját forgásból (perdületéből), aminek nagyságát az S.ħ spin adja meg. A mágneses momentum kifejezése:
μ = μB(L + 2S)
Itt μB = e.ℏ/(2m.c) a Bohr magneton.
A klasszikus elektrodinamika szerint a köráram által létrehozott mágneses momentum μ = j.f/c, ahol j = e.ν az áram, f = r2.π a köráram által bezárt terület. Ennek megfelelően a pályamozgás által létrehozott mágneses momentum:
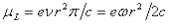
Vegyük figyelembe a klasszikus és a kvantummechanika impulzus momentum definícióit: L.ℏ = m.ω.r**2, ami elvezet a mágneses momentum pályajárulékának kifejezéséhez:

A gömbhéjon történő kettős forgás modellje annak felel meg, hogy az elektron töltése és tömege az r = R_c sugarú héjon helyezkedik el egyenletes eloszlásban. Ez abból következik, hogy tömeg a vákuumból csak úgy képződhet, ha a mozgás eléri a fény sebességét. Ennek járulékát a mágneses momentumhoz úgy számíthatjuk, ha a gömbhéjat körszeletekre vágjuk, az egyes szeletek köráramát pedig összegezzük, ekkor az eredmény megegyezik a pályamozgástól származó fenti formulával. Viszont a Dirac féle mágneses momentumban szerepel még egy kettes faktor a spin esetén, felmerül a kérdés, hogy honnan származik ez a kettes szorzó? Erre a kérdésre a klasszikus fizika látszólag nem tudja megadni a választ. A kudarc oka, hogy nem vettük eddig figyelembe, hogy az elektron spin nem egytengelyű, hanem kéttengelyű forgásból származik! Arról van ugyanis szó, hogy a mágneses tér körüli egytengelyű Larmor precesszió szuperponálódik a spint létrehozó kettősforgásra. A kettősforgás miatt feleződik az elektron spin, de ez a mágneses momentumra nem vonatkozik, hiszen a Larmor precesszió egy tengely – a mágneses tér – körül történik. Ezt figyelembe véve már eljutunk a Dirac egyenletnek megfelelő mágneses momentumhoz
μS = 2μB.S
A növekvő pontosságú kísérletekből azonban kiderült, hogy a Dirac egyenletből származó fenti kifejezés sem pontos, a tényleges együttható nem 2, hanem kissé nagyobb 2.0023…. Honnan származik ez a járulék? Ez a kérdés vált a QED elmélet próbakövévé. Ennek megértéséhez a mezőelmélet módszertanát kell követni. Eszerint a töltött részecskék közötti Coulomb kölcsönhatást virtuális fotonok közvetítik: az egyik elektron kibocsát egy fotont, amit a másik elnyel és ez az állandó foton csere hozza létre a taszítást, ha viszont különböző előjelű töltések vannak, akkor a vonzást. De ez csak a legegyszerűbb eset, az elektronok és a virtuális fotonok a közvetlen csatlakozáson kívül összetettebb utakat is választhatnak, sőt akár a virtuális fotonok átmenetileg létrehozhatnak elektron-pozitron párokat is. Ezek közül a legegyszerűbb, un. egyhurkos út adja az anomális momentum legfőbb járulékát, aminek értéke a Sommerfeld féle finomstruktúra állandóval arányos:
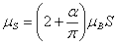
Értelmezzük ezt a további járulékot is a fénysebességű forgásokkal! Az elektron spinjének származtatásakor a végtelenül elfajult térgeometriából származó erős gravitáció és a kettős forgás centrifugális erejének egyensúlyából indultunk ki. De amint arra rámutattunk, fellép a Coriolis erő is, aminek csavaró hatása nyilvánul meg a Coulomb erőben, ami α mértékében gyöngébb az erős gravitációnál. Ennek hatása hozzáadódik a centrifugális erőhöz a mágneses tér iránya körüli 2π szögtartományban, amiért módosul az egyensúly
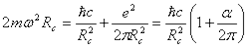
Ezt az összefüggést átrendezve kapjuk a mágneses momentum származtatásához szükséges kifejezést:
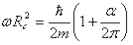
Evvel a gondolatmenettel illusztráltuk, hogy a fénysebességű kettősforgásokkal jól lehet szemléltetni a bonyolult mezőelméleti számítások eredményét, nem célunk azonban, hogy az anomális mágneses momentumra olyan teljes leírást adjunk, mint amire alighanem csak a komplett mezőelmélet képes
A QED elmélet sikerei mellett azonban divergencia problémák lépnek fel a sajátenergia számítása során. Ennek oka, hogy amikor felhordjuk a töltéseket egy gömb felületére végtelen távolságból indulva, akkor az elvégzett munka végtelenül nagy lesz abban az esetben, ha a gömb sugarát nullának vesszük, már pedig erre van szükség, mert a QED kiindulópontja az elektront pontszerűnek tekinti. Ez a probléma nem merül fel a fénysebességű forgásoknál, mert a mozgásirányra merőleges sugár nem redukálódik, miközben a felszín nullára zsugorodik. Másik lehetséges ok, amiért divergenciák lépnek fel a mezőelméletben, hogy nincs felső korlátja a virtuális fotonok energiájának. Fénysebességű forgásoknál viszont a virtuális fotonok energiája nem haladhatja meg a tér görbülete által stabilizálható mc2 értéket.
A spin függvények 4π szögű periodikusságának rejtélye
Az S = ½ spin hullámfüggvénye Ψ = exp(±½ϕ) rendelkezik egy különös tulajdonsággal: a 360 fokos, azaz 2π szögű forgatáskor előjelet vált és a függvény csak 720 fokos forgatáskor megy át önmagába. Ezzel szemben a pálya-impulzusmomentum operátor exp(iml Φ) függvényei „normális” módon viselkednek a teljes fordulat hatására, mert az ml kvantumszám csak egész értéket vehet fel. A különbség onnan adódik, hogy a pálya-impulzusmomentum egyetlen tengely körüli forgáshoz tartozik, szemben a spinnel, ahol a kettősforgatás miatt a Φ szögű transzformációt két tengely körül hajtjuk végre, és amíg az egytengelyű forgatások egy 2π kerületű kört alkotnak, addig a kéttengelyű forgatások egy kétdimenziós 4π felületű gömbfelszínt fednek le, ha a sugarat egységnyinek vesszük.
A hullámfüggvények szimmetria tulajdonságait a matematikai csoportelmélet segítségével aknázhatjuk ki, ahol azt vizsgáljuk, hogy milyen forgások és tükrözések viszik át a rendszert önmagába. Identitás műveletnek tekintjük, amikor nem változtatunk meg semmit, ilyen például szokásos esetben a 360 fokos forgatás. Mivel az S = ½ hullámfüggvény ekkor előjelet vált szükség volt a csoport műveleteit kiegészíteni a 2π forgatással is. Így jött létre a Bethe féle kettős csoport, amelynek un. „irreducibilis ábrázolásai” már kezelni tudták az olyan hullámfüggvényeket is, ahol a spin ½ volt. Ez a matematikailag korrekt, bár a józanész számára meghökkentő módszer, a kettősforgások koncepciójával már jól értelmezhető, hiszen ekkor tényleg csak a 4π forgatás lesz identitás művelet.
Miért rendelkezik az elektron S = ½ spinnel?
Forgások esetén a Lorentz kontrakció miatt a kerület olyan mértékben csökken, amilyen mértékben a tömeg nő, miközben a sugár állandó marad (lásd „Térgörbület és gravitáció forgó rendszerekben”. Fénysebességű forgásoknál ebből következik, hogy az impulzusmomentum a forgási frekvenciájától függetlenül mindig ℏ lesz egytengelyű forgások esetén, legyen szó akár gyenge rádióhullámokról, vagy kemény gamma sugárzásról, vagy a nagy tömegű gyenge kölcsönhatási bozonokról. Kéttengelyű forgásoknál az impulzusmomentum feleződik, azaz a spin ½ lesz, amit avval értelmezünk, hogy ekkor az erős gravitációnak két különböző forgás centrifugális erejét kell kiegyenlíteni. Az impulzusmomentum feleződését értelmezhetjük a tehetetlenségi nyomaték elvével is: a tehetetlenségi nyomaték és a forgási frekvencia szorzata adja meg az impulzusmomentumot. Egytengelyű forgás annak felel meg, mintha egy „karikát” a szimmetriatengely körül forgatnánk, amíg a kéttengelyű forgatás úgy fogható fel, hogy az első forgatás „karikáját” a második a főtengely körül perdíti meg. Az utóbbi esetben fele lesz a tehetetlenségi nyomaték és ezáltal az impulzusmomentum is.
Minek köszönhetjük, hogy a Dirac formalizmus is evvel egybecsengő eredményre vezet? Külső elektromágneses tér nélkül az elektron energiája nem függ az iránytól és ebből következően a relativisztikus invariancia felhasználásával generált mennyiségek, így a spin sem irányfüggő. Az irányfüggetlenség abban nyilvánul meg, hogy a spin három vetületének négyzete egyformának adódik
: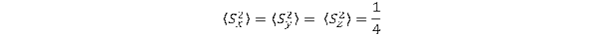
A három komponens négyzetösszege, azaz S2 viszont S(S+1) az operátorok felcserélési szabályai miatt. A két követelmény egyidejűleg csak S = ½ esetén teljesül. Ez azt jelenti, hogy az elektron izotróp szerkezete megköveteli, hogy S = ½ legyen. Ez összhangban van a kettősforgás koncepciójával is, mert az egytengelyű forgás nem lehet gömbszimmetrikus. A kettősforgás koncepcióját az is alátámasztja, hogy ekkor fellép egy jobb és egy balsodrású forgásállapot is, ami két részecske létezésére utal ellentétes előjelű töltéssel a Coriolis erő királis függése miatt. Ezért léteznek a részecske és anti-részecske párok.
A blog további bejegyzéseinek összefoglalóját lásd "Paradigmaváltás a fizikában"




