Az előző részben („A kvark színe”) a részecskék sajátmozgásait kapcsoltam össze a Standard Modellben összegzett tulajdonságokkal és erőhatásokkal, ebben a folytatásban a kvantummechanika matematikai formalizmusával alapozom meg az elmondottakat.

A mozgási és a nyugalmi tömeg 

A relativitáselmélet a tömeg két típusát különbözteti meg, az egyik a nyugalmi tömeg, ami azt mutatja meg, hogy a fizikai objektum saját rendszerében mekkora ez az érték. A másik a mozgási tömeg, ami a megfigyelt részecskéhez képest állandó sebességgel mozgó inercia rendszerben érvényes. A mozgási tömeg tetszőleges lehet, mert értéke attól függ, hogy éppen mekkora az a sebesség, amivel a részecske a megfigyelőhöz képest mozog, ezt a sebességet ugyanis tetszőlegesen inercia rendszerhez viszonyíthatjuk. A relativisztikus energia a sebességtől függő kinetikus energia és az attól független nyugalmi energia négyzetes összegéből számolható, amit c²-tel osztva kapjuk a teljes mozgási tömeget. 

Az elektron Dirac egyenlete 

Dirac relativisztikus hullámegyenletében a fentiek úgy jelennek meg, hogy egy 2x2 dimenziós mátrixalakban az m₀c² nyugalmi energia a diagonális, az impulzussal arányos relativisztikus  p.c mozgási energia a nem-diagonális pozícióban jelenik meg, másképp fogalmazva az előbbi a diagonális σ_z, az utóbbi a tisztán nem-diagonális σ_x  Pauli mátrixszal van megszorozva, ahol a két Pauli mátrix alakja: 

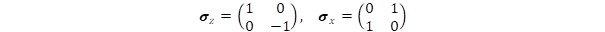
A diagonális mátrixszerkezetnek alapvető jelentősége van a kvantummechanikai operátorformalizmusban, mert a diagonális elemek felelnek meg az adott fizikai mennyiség mérhető sajátértékeinek. Dirac formalizmusában ezért az impulzustag nem diagonális szerkezete annak felel meg a relativitáselméletben, hogy az impulzus nagysága nem abszolút, hanem attól függ, hogy a tetszőlegesen választott inercia rendszerhez képest a fizikai objektum mekkora sebességgel mozog.

Az általános fermion egyenlet 

 „A Dirac egyenlettől az általános fermion egyenletig” című bejegyzésben vittem tovább Dirac eljárását annak érdekében, hogy tetszőleges elemi fermion (kvarkok és neutrínó) esetén is fel lehessen bontani az energiát nyugalmi és mozgási tagra. Ennek technikája, hogy a Dirac által bevezetett 4x4 dimenziós spinorok helyett 8x8 dimenziós spinorokat alkalmaztam, amelyek viszont felépíthetők három Pauli mátrix direkt szorzataként. Bevezettem a Pauli mátrixból felépíthető diagonális és nem diagonális elemeket egyaránt tartalmazó uniter mátrixot is: 

U_n = σ_z.cosρ + σ_x.sinρ és U^†_n = -σ_z.sinρ + σ_x.cos ρ 

Ez az uniter mátrix kerül a nyugalmi energia együtthatójába σ_z helyébe, míg ennek U^†_n  adjungáltja váltja fel σ_x-et p.c szorzójaként. A ρ szög értéke az n kvantumszámtól függ a cos ρ = n/3 szabály szerint, ahol n = ±3 felel meg az elektronnak és pozitronnak, n = ±2 az u, míg n = ±1 a d kvarknak és végül n = 0 a neutrínónak. Ily módon valamennyi elemi fermion elektromágneses kölcsönhatása egyetlen egyenlettel írható le. 

A tömeg és töltés kvantummechanikai operátora

 Az U_n uniter mátrix egyúttal az e töltés szorzójaként is megjelenik. Az eljárás a kvantummechanikai operátor technika továbbfejlesztését is jelenti, mert ezáltal a tömeg és a töltés is valós szám helyett operátor lesz, melyek definíciója:

m = U_nm   és q = U_ne

Az operátorként kezelt tömeg és töltés azt jelenti, hogy az energiaoperátor által kijelölt állapot határozza meg a két mennyiség várható értékét és annak a hibáját. Ha az m és q operátorok felcserélhetőek az energia operátorával, akkor a részecske tömege és a töltése pontosan megadható. Ez valósul meg az elektron és a pozitron esetében, ezért ezeknek a részecskéknek jól definiált tömege és töltése van, ami pontosan mérhető. A neutrínó képviseli a másik végletet, ekkor az impulzus tag lesz diagonális, míg a töltés és a tömeg tisztán nem-diagonális. Ez vezet oda, hogy a neutrínó töltésének és tömegének várható értéke nulla lesz, viszont impulzusa pontos értékkel rendelkezik. A részecskéket emiatt egy sajátos bizonytalansági reláció jellemzi, ami a relativitáselméletből következik: vagy a nyugalmi tömegük rendelkezik jól definiált értékkel és ekkor impulzusuk a választott inercia rendszertől függ, vagy impulzusuk független az inercia rendszertől, de ekkor a tömeg lesz a választott rendszer függvénye.  Ez feloldja a neutrínó oszcilláció értelmezése körüli zűrzavart. Nem azért létezik három különböző neutrínó, amelyek a kísérletek tanúbizonysága szerint egymásba periodikusan átmennek, mert van nyugalmi tömege a neutrínónak, hanem azért mert rendelkeznek három különböző sajátimpulzussal. Úgy is mondhatjuk, hogy a neutrínó „impulzus típusú”, az elektron és pozitron „tömeg típusú” részecske.

Kvarkok anomális töltése és a renormálási tömeg

A kvarkok külön esetet képviselnek, mert ekkor a tömeg és töltés operátor egyaránt tartalmaz diagonális és nem-diagonális elemeket és ez a helyzet az impulzussal is. Emiatt mind a tömeg és mind a töltés esetén nem az operátorok sajátértéke határozza meg ezeket a mennyiségeket, hanem az állapotfüggvénnyel értelmezett várható érték. Ez a várható érték adja ki a kvarkok anomális ±⅓e és ±⅔e töltéseit. A tömegek esetén is ez a helyzet, a Standard Modellből származtatott renormálási tömegek felelnek meg a várható értékeknek. Szabad kvark viszont azért nem figyelhető meg, mert a részecske nincs sem tömeg, sem impulzus állapotban, és így nem rendelkezik olyan tulajdonsággal, ami a detektáláshoz szükséges..

A tömeg és töltés operátorok fotonok és W bozonok esetén 

Érdemes még arra is rámutatni, hogy a tömeg és töltés operátordefiníciója alkalmazható fotonok esetében is. Ekkor a nulla nyugalmi tömeg és töltés annak felel meg, hogy a tömeg és töltésoperátor egyaránt tisztán nem-diagonális, így a két mennyiség várható értéke nulla lesz. Az impulzus azonban diagonális, ezért pontos értékkel rendelkezik és megadja a teljes energiát, illetve a mozgási tömeget. A gyenge kölcsönhatás W bozonja esetén megfordul a kép, mert ekkor a Pauli mátrix orientációját kijelölő haladási irány merőleges a fénysebességű forgás tengelyére. Ez a formalizmusban úgy jelentkezik, hogy a tömeg és töltés operátor diagonális lesz és így ezek a bozonok jól definiált tömeggel és töltéssel rendelkeznek, más szóval a W bozonok is tömeg típusú részecskék. Az egytengelyű forgások S = 1 állapotai azonban nem teljesen azonosak az S = ½ spinű kettősforgásokkal, ami abban mutatkozik meg, hogy létezik a semleges Z bozon, melyben a két kiralitás együtt szerepel és ekkor eltűnik a töltés, viszont szemben a neutrínóval a tömeg megmarad.

Az alábbi linkre kattintva lehet eljutni a "Paradigmaváltás a fizikában" című bejegyzésre, ahonnan további bejegyzésekre történik utalás.