Ha feldobunk egy követ, akkor a kezdeti lendület felfelé viszi, majd a haladás lassulni kezd, majd megáll és gyorsulva esik lefelé, ha fellövünk egy rakétát kellő sebességgel, akkor nem zuhan vissza, hanem elszakad a Földtől, de azt is megtehetjük, hogy vízszintes pályára álljon és keringjen Földünk körül. Mindegyik esetben a mozgási energia és a gravitáció potenciális energiájának egymásba alakulása írja le a folyamatot. Sokkal nagyobb méretekben is hasonló jelenség játszódik le az Univerzumban az ősrobbanás után.
A szökési sebesség
Nézzük először a földi példát, hogy könnyebben értsük az Univerzum korszakváltásait. Ha az m tömegű rakétát v sebességgel lőjük fel, akkor a kinetikus energia ½ m.v2 lesz. Az R = 6378 km sugarú Föld felszínén a potenciális energia V = G.m.M/R, ahol G = 6,67x10-11.m3/s2kg az általános gravitációs állandó és M = 5,97x1024 kg a Föld tömege. A rakéta elszökik a Földről, ha kinetikus energiája meghaladja a potenciális energiát, azaz
½ m.v2 > G.m.M/R
ahonnan a szökési sebesség v = 11,1 km/s a v2 = 2G.M/R összefüggés alapján. A pályára állítás sebessége ennél kisebb (7,86 km/s), amit a centrifugális erő és a gravitációs vonzóerő egyensúlyából számolhatunk ki:
m.v2/R = G.m.M/R2 , azaz v2 = G.M/R
Az Univerzum lehetséges modelljei
Az Univerzum kialakulása az ősrobbanás után természetesen ennél bonyolultabb jelenség. A hasonlóság annyi, hogy ekkor is három alapszcenárió lehetséges: a táguló, az összehúzódó és az egyensúlyi modell. A lehetséges modellek szempontjából az M tömeget az Univerzum teljes tömege, illetve homogén rendszert feltételezve annak sűrűsége képviseli, míg további fontos szerepet játszik az Univerzum teljes kiterjedésének „A” sugara.
Einstein gravitációs egyenlete
Mielőtt az Univerzum fejlődését tárgyalnánk, először lépjünk vissza az időben, amikor Einstein kidolgozta gravitációs elméletét. Ő a gravitáció eredetét a tér görbületével hozta kapcsolatba: szerinte a tömeg maga körül begörbíti a teret és emiatt nem az egyenes út lesz a mozgás legrövidebb útja, hanem az a trajektória, amely a görbületeket mentén halad. Einstein, amikor a csillagos égre nézett, úgy képzelte, hogy amit látunk az ősidők óta hasonló, bár a csillagok és galaktikák egymáshoz képest vándorolhatnak, de sűrűségeloszlásuk alapjába véve változatlan. Ebben az értelemben egyensúlyi világképben gondolkozott. De miért nem zuhan önmagába az Univerzum a gravitáció miatt, vagy miért nem szalad szét a benne rejlő kinetikus energia miatt? Azaz elgondolás, hogy az egyensúlyt a keringő mozgások miatti centrifugális erő tartja fent nem volt számára elfogadható, mert akkor a távoli galaxisok sebessége messze meghaladta volna a fény sebességét, ami pedig a speciális relativitáselmélet kiinduló pontja. Ezért gondolt egy merészet és feltételezte, hogy a térnek van egy immanens antigravitációs hatása, ami egyensúlyt alkot a gravitációval és létrehozza az „örök” Univerzumot. Ezt az elképzelést úgy valósította meg, hogy a gravitációs alapegyenletébe berakott egy új tagot, amit Λ-val jelölt, és amit kozmológiai állandónak nevezünk.
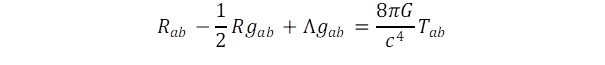
A fenti egyenlet magyarázatát korábbi írásomban („Einstein igazsága és tévedései”) már megadtam, de a könnyebb olvashatóság kedvéért újra összefoglalom a fontosabb megállapításokat.
A gravitációs egyenlet paraméterei
A tömegek pozíciója és sebessége adja a „forrást” az egyenlet jobb oldalán, amit matematikailag az energia-impulzus tenzor Tab ír le, ahol az alsó index a görbült téridő koordinátáit jelöli. Ez alapján kell meghatározni a gab metrikus tenzort, ami a koordináta szorzatok együtthatója. A speciális relativitáselméletben (Minkowski téridő) gab egy négydimenziós diagonális mátrix: (1, -1,-1,-1) sajátértékekkel, ahol az első index az idődimenziónak felel meg. Ha ismerjük a görbült tér gab metrikus tenzorát, akkor ebből parciális deriválások segítségével képezhetjük az Rab görbületi tenzort, amit Ricci tenzornak nevez az irodalom. A Λgab tag nem függ a görbületi tenzortól csak a metrikától és előjele pozitív, ami a taszítást (antigravitációt) jeleníti meg.
A Hubble-féle tágulási törvény
Néhány évvel Einstein publikációjának megjelenése után Hubble a távoli galaxisok vörös eltolódása alapján kimutatta, hogy az Univerzum nem sztatikus, hanem tágul. Einstein azonnal elismerte tévedését és a kozmikus állandó bevezetését élete legnagyobb tévedésének nevezte. Az utókor mégis igazat adott Einsteinnek a kozmológiai állandó létezését illetően, mert a távoli szupernóva robbanások vörös eltolódása arra mutat, hogy az Univerzum gyorsulva tágul, szemben a tisztán gravitációt feltételező modellel, amely lassuló tágulást hozna létre.
Hubble 1929-ben publikált megfigyelésének lényege, hogy minél távolabb van tőlünk egy galaktika, annak távolodási sebessége arányos a d távolsággal: v = H.d, ahol a H állandó értéke a legújabb mérések szerint H = 73,00±1,75 km/Mpc.s.
Az ősrobbanás elméletének születése
Érdekes módon a Hubble törvény magyarázata két évvel megelőzte a törvény megszületését, amikor Georges Lemaître 1927-ben Einstein általános relativitáselmélete alapján adott magyarázatot a spirális galaxisok távolodására. Felvetette az „ősatom” koncepcióját feltételezve, hogy a galaxisok távolodása az Univerzum alapjelensége, amit visszavetítve a messze múltba, kellett lenni egy olyan kezdő pillanatnak, amikor az összes galaxis egyetlen matematikai pont volt, amelyben az egész Univerzum összes energiája benne foglaltatott. Meghökkentő állítás, ha arra gondolunk, hogy milyen óriási energia van a Napban és a Nap csak egy szerény csillag a Tejútrendszer milliárd csillagja közül, és a galaxisok száma is eléri a milliárdot! Szabad-e ilyen messzire extrapolálni, mi a garancia arra, hogy a fizika törvényei változatlanok ilyen extrém körülmények között, amikor a nyomás, az anyagsűrűség és a hőmérséklet elképesztő mértékben megemelkedik?
Lemaître koncepciója szerint, amikor az „ősatom” szétszakad – később ezt nevezték el ősrobbanásnak – az egyes elemek minden irányban, de különböző sebességgel távolodnak az eredeti pozícióhoz képest. Ha például az egyik sebessége v1, a másiké v2, akkor T idő alatt v1T illetve v2T az eltávolodás a kezdőponttól és így a közöttük lévő távolság d = (v2 – v1)T arányos lesz a sebességkülönbséggel és a T idő – amit a mai számítások 13,788 milliárd évre becsülnek – a H állandó reciprokának felel meg, legalább is akkor, ha idő közben a sebességek nem változnak meg. Bár az egyes galaxisok távolságát saját magunktól mérjük, ebből nem következik, hogy magunkat tekinthetnénk az Univerzum centrumának, mert a távolodási törvény az Univerzum bármely pontjáról nézve azonos lesz.
Friedmann koncepciója az Univerzum tágulásáról
Alexander Friedmann orosz matematikus és fizikus foglalkozott avval a kérdéssel, hogy a Hubble állandó hogyan változik Einstein gravitációs egyenlete alapján. Az Univerzumot homogén és izotróp folyadéknak képzelte el, amelyben a galaxisok minden irányban és minden távolságban egyforma számban és sűrűségben találhatók meg. Számba vette a gravitáció és a kozmikus taszítási tagon kívül a fénynyomást és a tér görbületét leíró „k” faktor hatását is, ahol az utóbbi a sík euklideszi geometriában nulla, míg a két lehetséges előjelű görbületet +1 és -1 közötti érték írja le. A jelenkori H0-hoz viszonyítva adta meg a változó H értéket:
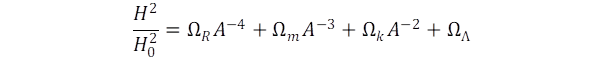
A tágulási paraméterek szemléletes értelmezése
A Friedmann egyenletet szemléletesen értelmezhetjük a bevezetőben bemutatott szökési sebességek alapján. A szökési sebesség négyzete függ az M tömeg és a Föld R sugarának arányától. A négyzetes összefüggés itt a H állandóban jelenik meg, az omega együtthatók hozhatók kapcsolatba a sűrűség jellegű mennyiségekkel, és fellép a formulában A, tehát az Univerzum teljes mérete, hasonlóan ahhoz ahogy a szökési sebességnél a Föld R sugara játszik szerepet.
Értelmezzük először A hatványait! Az első tag, ami a fénynyomás hatását írja le A-4-el arányos. Ennek oka, hogy egyrészt a nyomás az Univerzum felületével, vagyis A2-tel arányosan csökken, másrészt a fény intenzitása is csökken a galaxisok távolságának négyzetével. A második tag Ωm jellemzi az anyagsűrűség gravitációs hatását, itt A-3 azért lép fel, mert a sűrűség fordítva arányos a térfogattal. A harmadik tag, amelynek Ωk az együtthatója a tér görbületéből fakadó nyomást írja le és A-2 fejezi ki, hogy a nyomás fordítottan arányos a felülettel. Végül az ΩΛ tag nem függ az Univerzum méretétől, mert Einstein egyenlete szerint csak a metrika befolyásolja és nem számít, hogy lokálisan mekkora a tér görbülete. Úgy is felfoghatjuk ΩΛ-át mint az Univerzum születési energiáját, ami később sem változik meg.
Az Univerzum első korszaka: a fénynyomás uralma
Az Univerzum korszakváltásait kiolvashatjuk a Friedmann formulából! A kezdetekben, amikor az Univerzum parányi volt, az A-4 függés miatt a fénynyomás dominált és a tágulási sebesség rendkívül nagy értéket vett fel, ami sok-sok nagyságrenddel haladta meg a fény sebességét. Ezt a szakaszt, ami a számítások szerint a másodperc tört részéig tartott nevezzük az Univerzum inflációjának. De hogyan értelmezhetjük ezt a fénysebesség állandóságának törvényével? Korábbi írásokban már utaltam rá, hogy a maximális kölcsönhatási sebesség a biztosítéka, hogy az Univerzum nem robban fel, hiszen ha nincs felső határ, akkor minden hatásra késletetés nélkül jön a válasz, amelynek végtelenhez tartó összege szétrobbantaná az Univerzumot! De hát a kezdeti szakasz, amely a másodperc töredékéig tartott nem más mint maga a robbanás! A fénynyomás uralkodásának korszakában az Univerzumban nem volt, ami korlátozta volna a fényt.
Volt- az Univerzumnak Planck korszaka?
Az Ősrobbanás elmélete megáll a Planck időnél:
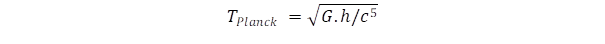
mert ezelőtt már a kvantummechanikai bizonytalanság miatt elmosódnak a határok, de ha a fénynyomás korszakban a végtelenhez fut a sebesség, akkor ez az idő nulla felé tart. Lehet, hogy emiatt nem is beszélhetünk az Univerzum Planck korszakáról, mert tetszőlegesen rövid ideig haladhatunk az elmélettel az ősrobbanás kezdete felé.
Az Univerzum gravitációs korszaka
Az Univerzum túlélte ezt a korszakot, ami alatt mérete óriásira nőtt, és lecsökkent a kezdeti hatalmas sűrűség és hőmérséklet, és ennek következtében beindulhatott először az elemi részecskék, majd később az atomok felépülése, kialakulhattak a csillagok és galaxisok is. Erről írtok részletesebben „ Az ősrobbanás és a teremtésmítoszok” című bejegyzésben. Ekkor jött el a második korszak, amikor az anyag gravitációs hatása dominálta már az Univerzumot. Ebben a korszakban már nem a fény volt az úr és sebességét a gravitáció visszafogta és már nem kellett tartani újabb robbanástól. Ez már egy konszolidált Univerzumot hozott létre, ekkor az Univerzum tágulási üteme is lassulni kezdett.
Az Univerzum antigravitációs korszaka
A jelenlegi kozmológiai elmélet szerint ez a szakasz hét és fél milliárd évig tartott és utána a tágulási sebesség gyorsulni kezdett és ez folytatódik napjainkig is. Ebben a korszakban az antigravitáció már hatásában túlnő a gravitáción, aminek oka, hogy ΩΛ nem függ az Univerzum méretétől. A sokasodó és egyre pontosabb csillagászati megfigyelések fokozatosan pontosítják az Univerzum tágulásáról szóló ismereteinket. Felmérték, hogy az átlagos sűrűség annak felel meg, hogy 0,2 proton jut minden köbméterre, viszont a megfigyelt tágulási sebességhez ennél sokkal többre lenne szükség, mintegy 5 protonnak megfelelő tömegre. Kell tehát lenni egy olyan anyagnak, ami kibújik a megfigyelések alól, ezt nevezték el sötét anyagnak, ami a teljes tömeg 95 százalékát képviseli. Más számítások az antigravitáció hatását vetették össze a gravitációval és azt kapták, hogy a tér szerkezetéhez kapcsolható antigravitáció – amelynek energiáját „sötétnek” nevezi a szakirodalom – szintén túlsúlyban van és az Univerzum teljes energiájának 69 százalékát teszi ki.
Nem ejtettünk szót a görbületi nyomásról, amely szintén a gravitáció hatása fölé nőhetne az A-2 függés miatt. Viszont a kis átlagos anyagsűrűség következtében az Univerzum görbülete csak lokálisan lehet nagy a fekete lyukakban, de összességében a tér geometriája közel van a síkhoz és emiatt hatása nem lehet jelentős.
Záró gondolatok
Fizikai világunkat négy különböző erő szabályozza: a gravitáció, az elektromágneses kölcsönhatás és az elemi objektumok erős és gyenge kölcsönhatása. Ezek közül a gravitációnak hármas arca van. Az egyik az elemi részecskék sajátmozgásának stabilitását biztosítja, ez az erős gravitáció. A másik hétköznapi világunkban fejti ki hatását, ez az erő, amely minket a földhöz tapaszt, de ez forrasztja össze az anyagot bolygókká, csillagokká és galaxisokká, és ez szabályozza kölcsönös mozgásukat. De van egy harmadik arca is, amelyik a galaxisok világában fejti ki hatását, távol tartja egymástól őket és nem engedi, hogy egymásba zuhanjanak. Ez gondoskodik az egész Univerzum stabilitásáról és ez jelenik meg Einstein gravitációs egyenletében a kozmikus állandó, azaz a lambda tag képében.
A blog egyéb írásait összegzi és megadja a linkeket a „Paradigmaváltás a fizikában” című bejegyzés



