Az állandóság keresése a változásban

Világunk állandó változásban van, de ha meg akarjuk érteni, akkor keresni kell, hogy mi az állandó a változások mögött. Ezt keresi a fizika is, amikor kialakítja a maga saját fogalomrendszerét. Az út fontos állomása a nyugalmi energia. De hát lehet a nyugalom az energia forrása?  Ennek megértéséhez először fussunk végig a mechanika fogalmain a klasszikus felfogástól kezdve a relativitás elvéig.

Az erő mint a változás oka

A világot annak teljes összefüggő rendszerében nem tudjuk leírni, ezért megkülönböztetünk benne elkülönült komponenseket. Mindenekelőtt magunkat elválasztjuk a külvilágtól és a valóságot a kívülről érkező hatások alapján írjuk le. A külső világot felosztjuk fizikai objektumok sokaságára és keressük közöttük a kölcsönhatásokat, amelyeket törvényekbe foglalunk. Feltesszük a kérdést, hogy mi hozza létre a kölcsönhatásokat az objektumok között, amit erőnek nevezünk. Erő, ami a földhöz tapaszt minket, erő, amit a gyorsuló járműben, vagy a körhintában érzünk, de erők kapcsolják össze és alakítják át a legkisebb elemi részecskéktől kezdve egészen a leghatalmasabb objektumokat, a galaxisokat is. Az erő mozgásokat hoz létre, az erő hiánya, vagy különböző erők egymást kiegyenlítő hatása esetén nem változik meg a mozgás jellege. Ebből indult ki Newton is, amikor megfogalmazta a maga  mozgástörvényeit.

Sebesség, gyorsulás, tömeg

Az erő által okozott mozgásváltozást a mechanika vizsgálja. Első lépésben leválasztja a mozgást gátló erőket, a súrlódást és a közegellenállást és az egyenletes sebességű mozgást tekinti a változatlan mozgási állapotnak és az erő hatását azáltal jellemzi, hogy mekkora változás következik be a sebességben, azaz mekkora a gyorsulás. Ugyanaz az erő az egyik tárgyat jobban, a másikat kevésbé gyorsítja fel, ami elvezet a tehetetlenség, a tömeg fogalmához. Így jutunk el Newton második törvényéhez, amelyben a tömeg az erő és a gyorsulás arányát fejezi ki: m = F/a. A tömegre egy fontos szabály érvényes: ha több testet együtt gyorsítunk fel, akkor a tömegek összeadódnak.

Az impulzus a mozgásmennyiség mértéke

A mechanika következő fogalmát a golyók rugalmatlan ütközéséből vezethetjük le. Vízszintes terepen gurítsunk el egy m₁ tömegű golyót v₁ sebességgel. Ha a súrlódástól eltekinthetünk és nem hat rá külső erő, akkor Newton első törvénye szerint a golyó sebessége állandó marad. Ütközzön a golyó egy m₂ tömegű álló golyóba – még pedig rugalmatlanul – ami azt jelenti, hogy az ütközést követően a két golyó összetapad és együtt halad tovább. Mérjük meg az ütközés után a most már m₁+m₂ tömegű golyó sebességét, azt találjuk, hogy a sebesség

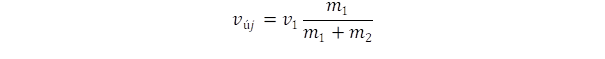
lesz, vagyis átírva:  m₁.v₁ = (m₁+m₂)v_új . A kísérletet megismételhetjük úgy is, hogy mindkét golyó mozogjon. Valamennyi ütközésnél azt tapasztaljuk, hogy a golyók összetapadása után akkora lesz a sebesség, ami megfelel az

m₁.v₁ + m₂.v₂ = (m₁+m₂)v_új

szabálynak. Ebből azt a tanulságot vonhatjuk le, hogy ha a tömeg és sebesség szorzatait összeadjuk a két golyó ütközése előtt és utána, akkor az összeg nem változik. Evvel a mozgásmennyiség fontos jellemzőjéhez jutottunk, az impulzushoz, amit a mozgó golyók tömegének és sebességének szorzata fejez ki: p = m.v.

Az impulzus fogalmára általánosabb definíciót is adhatunk, amelynek érvényessége tetszőleges ütközésre, így a rugalmas ütközésre is érvényes: az impulzus olyan fizikai mennyiség, amely megmarad amikor nem hat a vizsgált objektumra külső erő.

A rugalmas ütközés megmaradási szabályai

Most térjünk át a rugalmas ütközések esetére, amikor az v₁ és v₂ sebességgel ütköző golyók nem sérülnek és az ütközést követően valamilyen v’₁ és v’₂ sebességgel haladnak tovább. Használjuk fel az impulzusmegmaradás törvényét, mely szerint

m₁.v₁ + m₂.v₂ = m₁.v’₁ + m₂.v’₂                                                     (1)

A rugalmatlan ütközés esetétől eltérően, ahol az impulzusmegmaradás törvénye elég volt, hogy meghatározzuk az összetapadt golyók sebességet, most ez nem lehetséges, mert két független sebességet kell meghatározni. A klasszikus fizika alapelve, ha egy kísérletet azonos körülmények között megismétlünk, akkor az eredménynek azonosnak kell lenni. Ez azt jelenti, hogy létezik valamilyen további törvényszerűség, amely pontosan meghatározza, hogy mekkora lesz az ütközés után a két golyó sebessége külön-külön. Különböző tömegű és sebességű golyók esetén elvégezve az ütközéses kísérletet, azt fogjuk tapasztalni, hogy létezik egy második megmaradási törvény is, amely kimondja, hogy ha a tömeget a sebesség négyzetével szorozzuk, akkor ezek összege az ütközés során nem változik:

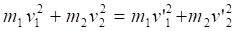
Ez a második megmaradási törvény vezet el a mozgási energia fogalmához, amely az impulzusmegmaradási törvénnyel együtt egyértelmű leírást ad a rugalmas ütközés kimenetelére. A kissebességű folyamatokban, ahol nem relativisztikus közelítést alkalmazunk, a mozgási energia kifejezésében fellép az ½ faktor is.

Energiamegmaradás és a hőenergia

Ha nem hat a golyókra külső erő és az ütközés tökéletesen rugalmas, akkor a mozgási energia megmarad. A rugalmatlan ütközésben azonban a mozgási energia jelentős részben elvész. Az energiamegmaradás törvénye ilyenkor azt jelenti, hogy a mechanikai energia részben rendezetlen mozgássá, azaz, hőenergiává alakul át, ami azonban nem jár impulzusveszteséggel. Az impulzus azért nem változik meg, mert a rendezetlen mozgásban a golyót alkotó részecskék (molekulák) minden irányban egyforma valószínűséggel mozognak és hatásuk átlagban nulla lesz. Evvel szemben az egyes részecskék mozgási energiája a sebesség négyzetével arányos, amely nem függ az iránytól és csak pozitív lehet. Az egyes részecskék mozgási energiájának összegét nevezzük hőenergiának.

Az erő és az impulzusváltozás

Ha valamilyen erő hat a testre, akkor annak mozgási sebessége megváltozik, amit az impulzusváltozással, vagy pontosabban szólva az idő szerinti differenciálhányadossal jellemezhetünk: F = dp/dt. Nem relativisztikus esetben ez a már említett F = m.a erőtörvénynek felel meg – de szemben az erő és gyorsulás kapcsolatát megadó törvénnyel – az erő és impulzusváltozás arányossága a relativisztikus mechanikában is fennáll.

A fizikai munka és a potenciális energia

Az erőhatását leíró potenciális energia fogalmához a fizikai munkavégzés segítségével jutunk el. Ha felemelünk egy testet, akkor a gravitációs erővel szemben végzünk munkát és ezáltal a test potenciális energiáját növeljük meg. Ha elengedjük a testet, akkor gyorsuló mozgással leesik, azaz mozgási energiára tesz szert a potenciális energiacsökkenés révén. A gravitációs erőt az F = - m.g adja meg (g a földi gravitációs gyorsulás), ahol a negatív előjel fejezi ki, hogy az erő iránya lefelé mutat. Ha z magasságba emeljük fel a tárgyat, akkor m.g.z munkát végzünk, tehát ez lesz a potenciális energia. A potenciális energiát a z változóval deriválva d(m.g.z)/dz = m.g értéket kapunk, ami az erő kifejezése fordított előjellel. Ezt fejezi ki az a megfogalmazás, hogy az erő a potenciális energia negatív deriváltja. (Általános esetben vektorokat kell alkalmazni az erő irányának jellemzésére, amelyet a potenciális energia negatív gradiense határoz meg). A test mozgása során, ha a potenciális energia és a mozgási energia összegét képezzük (itt a (2) egyenletben az ½ faktor fog szerepelni), akkor az erőtörvény alapján kimutatható, hogy a mozgás során ez az összeg állandó marad. Az energiát tehát két tagból építjük fel: az egyik felel meg az erő sebességváltoztatási képességének, ez a potenciális energia, a másik pedig a már létrehozott mozgást jellemzi, ez a mozgási, vagy kinetikus energia.

Változik-e a tárgyak hossza, ha mozognak?

A hétköznapi tapasztalataink alapján megalkotjuk a tér fogalmát, amelyben elrendezzük a tárgyak egymáshoz képesti helyzetét, míg az idő segítségével rakjuk sorba az eseményeket és különböztetjük meg az okot és az okozatot. Köznapi gondolkozásunkban nem merül fel a gyanú, hogy más képet kellene alkotunk a környező világról, amikor benne vagyunk, vagy amikor mozgás közben szemléljük. Ennek szemléltetésére képzeljük el, hogy egy v sebességű vonaton utazunk és az ablakból kinézve akarjuk meghatározni két pózna távolságát. Tegyük fel, hogy pontosan ismerjük a sebességet és mérjük a Δt idő különbségét, amikor elhaladunk két pózna mellett, ekkor a távolság Δs’ = v. Δt. Fel se merül bennünk a kétség, hogy ez a távolság más lenne, ha egy mérőrúddal kint határoznánk meg a póznák Δs távolságát. Pedig a relativitáselmélet pont ezt mondja ki, amikor bevezeti a Lorentz kontrakció fogalmát, mely szerint:

A formula reciproka  adja meg a Lorentz kontrakció mértékét, ami akkor válik jelentőssé, ha a v sebesség értéke közel van a c fénysebességhez. Emiatt van, hogy a megszokott körülmények között elhanyagolhatjuk a redukciót, hiszen, még az űrhajók sebességén is rendkívül csekély a rövidülés:

1/ β = 0,999 999 995

A Galilei és a Lorentz transzformáció

Ha a póznák távolsága 1 méter, akkor méterrudunk hossza látszólag megrövidül. Mérjük meg a pozíciónkat és a megtett utat evvel a rövidebb méterrúddal, ekkor számszerűleg nagyobb értékeket kapunk. Nem-relativisztikus közelítésben, ha s méri a kezdeti pozíciónkat és t idő telik el, akkor a kezdeti, már hátrahagyott helyzetnek megfelelő pozíciót a vonatból az s’ = s — v.t összefüggés határozza meg. Ezt szokás Galilei transzformációnak is nevezni. Relativisztikus esetben a rövidebb méterrúd miatt ez β szorosára növekszik:

s’ = β(s — v.t)                                                               (4)

Ami még szokatlanabb, hogy óránk is más ütemben ketyeg a nagysebességű vonaton, sőt a mért idő még attól is függ, hogy hol volt a kezdeti pozíciónk:

t’ = β(t — v.s/c²)                                                              (5)

A (4) és (5) összefüggéseket nevezzük Lorentz transzformációnak. A Galilei transzformációban természetesen t’ = t. A (4) és (5) transzformációkban a tér és idő tehát kölcsönösen függ egymástól, míg a Galilei transzformációban a kapcsolat aszimmetrikus. Minkowski azért vezette be a téridő fogalmát, hogy a tér és idő dimenziók elválaszthatatlan kapcsolatát hangsúlyozza a mozgások leírásában. Érdemes rámutatni, hogy az elektrodinamika alapegyenletei, a Maxwell egyenletek már eleve a Lorentz transzformáció szabályának engedelmeskednek. Ennek oka, hogy ezek az egyenletek már a fény terjedési szabályait is leírják, már pedig a fény terjedése igazán relativisztikus, hiszen épp innen származik a  c sebesség.

Az idő dilatáció szemléletesebb összefüggéséhez juthatunk (5)-ből, ha az s = v.t összefüggés alapján átalakítjuk a transzformációs formulát:

t’ = βt(1 – v²/c²) = t/β                                                                   (6)

Innen láthatjuk, hogy az idő dilatáció mértéke voltaképp megegyezik a hosszúság (3) szerinti Lorentz kontrakciójával.

Mit értünk kovariáns alatt a relativitáselméletben?

             Alkalmazzuk a (4) és (5) Lorentz transzformációt, hogy felépítsünk egy speciális mennyiséget, amely független lesz attól, hogy mekkora a választott inercia rendszer v sebessége, amelyben a méréseket végezzük.(inercia rendszerről beszélünk, ha a sebesség nem változik): Ez a mennyiség:

c²t² – s² = c²t’² – s’²                                                                   (7)

Ezt a kifejezést nevezik a relativitáselméletben kovariánsnak. Einstein mutatta ki, hogy ez a kovariancia a fénysebesség állandóságából következik, azaz bármekkora és bármilyen irányú inercia rendszerből is származik a fénysugár, annak sebessége vákuumban mindig pontosan ugyanakkora. Ebből következik, hogy a fénysebesség nem fokozható azáltal, ha mozgó objektumból bocsátjuk ki. Ez is meglepő állítás, pedig valójában természetesen következik az univerzum létezéséből. Ha a kölcsönhatások sebességének nem volna felső határa, akkor a hatásokra érkező viszontválaszok végtelen sokasága egy időben jelentkezne, ami vagy felrobbantaná, vagy megszüntetné az univerzumot.

Az energia és impulzus kapcsolata a relativitáselméletben

A relativitáselmélet másik alapvető kovariánsa az energiából és az impulzusból épül fel:

E² – p²c² = állandó = E₀²                                                                  (8)

Az inercia rendszer választása egyaránt megváltoztatja az energiát és az impulzust, hisz mindkét mennyiség az objektum sebességétől függ, de a négyzetek különbsége mégis állandó marad. Ha a kvantummechanikai operátorok definíciójából indulunk ki, amely szerint az energia a t időszerinti, az impulzus az s hosszúság szerinti differenciállal arányos, akkor a (8)-ban megadott kovariáns tulajdonképpen a (7) kovariáns differenciális alakja. A (8) egyenletben szereplő állandó képezi az objektum nyugalmi energiáját.

A tömeg sebességfüggése

A relativitáselmélet legfőbb megállapítása, hogy az energia és a tömeg fogalma összekapcsolódik a nevezetes E = m,c² összefüggés szerint. Ez kapcsolja össze a nyugalmi energiát és az m₀  nyugalmi tömeget: E₀ = m₀c², és helyettesítsük be (8) egyenletbe az impulzus p = m.v alakját, ami által eljutunk a tömeg sebességfüggési törvényéhez:

m²c² – m²v² = m₀²c⁴, azaz  m² = m₀²c²/(1 – v²/c²) =   β²m₀²                               (9)

A tömeg sebességtől való függése miatt a golyók rugalmas ütközésénél bevezetett és a mozgási energiához vezető (2) egyenlőség csak közelítőleg érvényes. Az energia-impulzus kovariáns alapján az energia kifejezése: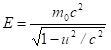

Kis sebességeknél eltekinthetünk a tömeg sebességfüggésétől és felírhatjuk a négyzetgyök Taylor sorát

:

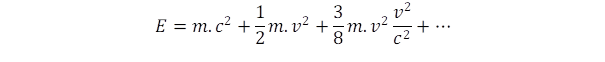
A nem-relativisztikus energiában innen származik az ½-es faktor, a következő tag pedig a relativisztikus korrekció.

További következménye a tömeg sebességfüggésének, hogy a newtoni F = m.a egyenletnél általánosabb az erő és az impulzus differenciálhányadosa közötti összefüggés, hiszen ekkor a tömeg idő szerinti differenciálását is figyelembe kell venni.

Honnan származik a nyugalmi energia?

Most már rátérhetünk a címben felvetett kérdésre, hogy mi is a nyugalmi tömeg és nyugalmi energia forrása? A fizikában az energiaformák egymásba alakulásáról beszélünk, a potenciális energia átalakul a mozgási energiává, a mozgási energia hőenergiává alakulhat át és még sorolhatnánk. Minden esetben a mozgás a kulcsszó, de mit kezdjünk a nyugalmi energiával, amikor az energia nem más mint a mozgás legfőbb megjelenési formája? Már ez a logika is arra ösztönöz minket, hogy a „nyugalmi” energia mögött is valamilyen mozgást keressünk! Mégpedig nem akármilyen mozgást, hiszen óriási energiáról van szó!.

 Amikor kémiai reakciókban energia szabadul fel, akkor megfigyelhető, hogy a képződő vegyületek össztömege egy milliárdod résszel kisebb, mint  amiből létrejött, amikor egy nehéz radioaktív atom szétbomlik, akkor a töredék atommagok tömegösszege ezrednyivel kisebb, mint a széteső atom, ami hatalmas energia kibocsátást eredményez, még több energia szabadul fel, amikor a legkönnyebb atomok hélium atommagot hoznak létre a fúzió során, mert ilyenkor már 1 százalék körül van a tömegdeficit, de a legnagyobb tömegvesztés az anyag-antianyag annihilációban jön létre, amikor a teljes tömeg eltűnik. A tömegdeficit minden esetben a képződő mozgási és hőenergia forrása. Ebben az értelemben a tömeget, mint potenciális energiát tekinthetnénk, de zavaró, hogy az energia formulákban mindig a potenciális energia lineárisan összegződik a többi taggal, míg a (8) összefüggés szerint négyzetes összegzési szabály érvényesül. Már ez is arra utal, hogy ne potenciális energiaként tekintsünk a nyugalmi energiára, hanem mozgási energiaként.

A fénysebesség szerepe a nyugalmi energia kialakulásában

Ha az elemi részecskék tömegét mozgásként akarjuk értelmezni, csak a fénysebesség jöhet szóba. Miért? Azért mert ez az egyetlen abszolút sebesség, minden más sebesség attól függ, hogy milyen inercia rendszerből nézzük. A fénysebesség viszont a téridő alapsebessége. Evvel rendelkezik a foton is. A fénysebességű mozgás a relativitáselmélet szerint szingularitást jelent, mert ekkor a β tényező végtelen lesz. Emiatt bármely nyugalmi tömeg végtelen lenne a (9) összefüggés szerint. A fotonnak ezért nincs is nyugalmi tömege, de van energiája a h.ν szabály szerint (h a Planck állandó és ν a frekvencia), de hát akkor mégis van tömege, ha az E = m.c² törvény minden fizikai objektumra, így a fotonra is érvényes. Az egyetlen lehetőség az ellentmondás feloldására, ha azt tételezzük fel, hogy a végtelenbe futó β a fénysebességű mozgásokban egy határértékben nulla értékkel szorzódik, ami által a szorzat véges értékű lesz, mint ahogy β*1/β = 1, akkor is, ha β határértékben végtelen! De mi lehet ez a határértékben nulla tömegű objektum, ami tömegre tesz szert a fénysebességű mozgás által? Van valami rejtélyes eredetileg nulla tömegű anyag a térben, amely fénysebességű mozgásba lendül?

A tér és idő fogalmaink kialakulása

De hogyan is alakult ki fogalmi rendszerünk a térről és az időről? Szemünkbe minden pillanatban óriási mennyiségű foton érkezik, amit szemlencsénk a retina különböző pontjaira vetít. Ez az információ az idegpályákon az agyba jut, ott feldolgozásra kerül, majd kialakul a kép, amely összegzi az optika szabályain alapulva, hogy honnan is érkeztek az egyes fotonok. Az így létrejött térképzet kiegészül egyéb érzékszerveink által nyert információval is. De ez a tér sztatikus, olyan, mint egy tartály, amelyben elrendezzük a tárgyak helyét és mozgását, és erre a térképzetre épül a részecskefizika is, amikor az anyag legkisebb objektumainak tulajdonságait vizsgálja. Térképzetünk jelentősen tovább fejlődött a nagysebességű mozgások értelmezésére létrejött relativitáselmélet által, ezáltal jutottunk el a téridő fogalmához, amelyben a tér, az idő és a mozgás már elválaszthatatlan egységet alkot, de még ez a kép is úgy kezeli a részecskéket, mint amelyek „benne vannak” a térben.

A dinamikus tér fogalma

Az előbbiekben felvetettem a kérdést, hogy mi azaz „anyag”, amiből a fénysebességű mozgás létrehozza a részecskéket. A választ a tér fogalmának kiterjesztésében keresem, amely nem puszta „tartály”, hanem maga is dinamikus fogalom, amely lokálisan fénysebességű saját mozgásokat végez. Ennek a térnek immanens tulajdonsága, hogy a fénysebességű mozgások által tömegre, energiára, impulzusra, impulzusnyomatékra (spinre) és töltésekre tesz szert. Több korábbi írásban („Az elemi részecskék mozgásformái”, „ A tér szerkezete és az elemi részecskék mint rezonanciák”, „ Téridő-részecske”, Fénysebességű forgások és a relativitáselmélet„”) már ismertettem ezt a modellt, amit fénysebességű forgásmodellnek hívok. Különböző módon kapcsolódhat össze két mozgásforma: a forgás és a haladás, és ez határozza meg, hogy fotonokról, illetve egyéb kölcsönhatást közvetítő bozonokról beszélünk, vagy fermionokról, mint az elektron, pozitron, neutrínó, vagy akár a kvarkok. Tehát nem arról van szó, hogy vannak térben mozgó részecskék, hanem arról, hogy a tér maga sajátforgásai által hozza létre a részecskéket. Ez a sajátforgás lesz a nyugalmi tömeg forrása is. Tehát a nyugalmi tömeg éppen hogy nem a nyugalomban lévő részecske tartozéka, hanem a fizikailag létező lehető leggyorsabb forgás! Amikor tömegdeficit jön létre, vagy a tömeg teljesen eltűnik, akkor ez az óriási sebességű forgás lesz a forrása az átalakulások során képződő sugárzási és mozgási energiának.

:

A korábbi bejegyzések összefoglalását és a megfelelő linkeket lásd: „Paradigmaváltás a fizikában: téridő görbülete kontra kvantumelv”.