Tévedések és tudományos előrehaladás
Tudományos előrehaladás nem lehet meg tévedések nélkül. Amíg eljutunk az igazsághoz gyakran kell végigjárnunk sok tévesnek bizonyuló mellékutat. Minden kutató, amikor valamilyen eredményre jut, állandóan felteszi magának a kérdést: vajon nem tévedek? Nincs olyan elmélet, nincs olyan állítás, amelynek igazsága ne lenne megkérdőjelezhető. Ezért minden kutató újra és újra végigszalad a bizonyítékok rendszerén vajon nem csúszott be valamilyen hiba az eljárásba, nem hagyott-e figyelmen kívül valamit, ami cáfolhatja elgondolásait? Ez az alkotó bizonytalanság, ami túllendítheti a kutatást a holtpontokon, ami elvezethet új eredményekhez, nagy felfedezésekhez is. Bátorság kell az új eredmények kimondásához, bátorság kell a tévedések beismeréséhez is. Akiből hiányzik ez a kettős bátorság nem érhet el igazán jelentős eredményeket. Minden új eredménynek, forradalmian új gondolatnak meg kell vívnia harcát, hogy befogadja a tudományos közgondolkozás. A közgondolkozás alapvetően konzervatív, emiatt gyakran hosszú időre van szükség, amíg egy-egy új koncepció beépül a tudományba. Ez helyes is, mert egyébként túl nagy teret kapnának a „meg nem gondolt gondolatok”, a tetszetősnek tűnő, de hibás, leegyszerűsítő elképzelések, a sajtó által gyakran felkapott áltudományos nézetek.
Mihez kell bátorság a kutatásban?
Nagy bátorságra van ahhoz is szükség, hogy valaki beismerje tévedését, ha kiderül egy hosszan dédelgetett elképzelésről, hogy téves, szemben áll újabb megfigyelésekkel, vagy elméletekkel. Ha valaki erre nem képes nem léphet tovább, akkor elveszíti képességét, hogy új eredményekhez jusson. Nem könnyű megmondani, hogy hol van a határ, hiszen a cáfolat sem abszolút, a cáfolat is cáfolható. Lehet, hogy az először elvetett gondolat végül mégis igaznak bizonyul. Nehéz megvonni a biztos határt. Minden kutatónak önmagával szemben kell kritikusnak lenni. Ennek igazi jutalma, ha hosszas küszködések és tévedések sorozata után valami hirtelen megvilágosodik, ekkor mintha kinyílna előttünk egy új és szebb világ és ebben a megszentelt pillanatban szárnyalni kezdenek az új gondolatok. Ez az a pillanat, amikor a kutató boldognak érezheti megát.
A speciális relativitáselmélethez vezető út
Einstein esetében két példában fogom illusztrálni a bevezetőben megfogalmazott gondolatokat. Az első példa a gravitációs hullámok lehetőségének felvetése volt. A kérdés előzményéhez tartozik a speciális relativitáselmélet megalkotása. Ez csírájában az elektrodinamika Maxwell egyenleteiben már megjelent, mert az elektromos és mágneses mezők differenciálegyenletei úgy kapcsolják össze az teret és az időt, ahogy azt a relativisztikus mechanika is megteszi a kovariancia elvén keresztül. Ezt ismerte fel Lorentz a maga transzformációs törvényével, ami alapján Minkowski bevezette a téridő fogalmát, Poincaré a matematikai formalizmus újította meg és Planck eljutott a tömeg és az energia ekvivalenciájának felismeréséhez az E = m.c2 összefüggés által. Einstein volt, aki a különböző elképzelések egységét teremtette meg és kimondta az alapvető elvet, ami a relativitáshoz vezet, nevezetesen a fénysebesség állandóságának törvényét. Kimutatta, hogy valamennyi relativisztikus jelenség mögött, ez az elv fedezhető fel.
A relativitáselmélet speciális változata csak részben „relativisztikus”. Ez alatt azt értem, hogy a törvény független attól, hogy a földi körülmények között, vagy az univerzum bármely pontján alkalmazzuk, csak az a fontos, hogy legyen a vonatkoztatási rendszer sebessége állandó, másképpen szólva alkosson inercia rendszert. Ekkor megadhatjuk a tér és idő koordináták sebességtől függő összefonódását, amikor is a tér koordináták részben átmennek az idő koordinátába és fordítva az idő is részben tér jellegűvé válik. Ennek következtében a megfigyelőhöz képest valamilyen sebességgel mozgó test mérete a megfigyelő mérései szerint lecsökken és tömege megnövekszik.
Miért volt szükség a speciális relativitáselmélet általánosítására?
Einstein tisztában volt a speciális relativitáselmélet korlátaival is, mert a feltételezett inercia rendszer valójában nem is létezik. A Földhöz nem köthetjük, mert a Föld forog saját tengelye és kering a Nap körül, a Nap sem jó választás, mert keringő mozgást végez a Tejút rendszerben, a Tejút középpontja sem jó, mert a különböző galaktikák egymáshoz képest is végeznek különböző nem egyenletes sebességű mozgásokat. Ezért szükségét látta, hogy olyan elméletet dolgozzon ki, amely a gyorsuló vonatkoztatási rendszerben is alkalmazható. Ezt kapcsolta össze a gravitáció eredetének magyarázatával. Kimondott egy általános elvet, ami megalapozta az általános relativitáselméletet: a gravitáció ekvivalens a gyorsuló rendszer tehetetlenségi erejével. Ezt úgy szemléltethetjük, ha valaki egy űrhajóban utazik távol minden gravitációs mezőtől és az űrhajó pont a földi nehézségi gyorsulással halad, akkor ugyanakkora erő hat rá, mintha a Földön lenne. Az ekvivalencia elv azonban magával hozta a tér és idő összekapcsolásának új formáját, ezek a koordináták másképpen csatolódnak össze, amikor a szóban forgó rendszerben fellép a gravitáció, illetve a gyorsulás. Ez a másféle kapcsolódás a téridő koordináták lokális görbületével írható le. Az ekvivalencia elv szerint nem számít az anyag minősége, csupán a tömege. A tér nem jellemezhető az euklideszi egyenes koordinátákkal a téridőt torzító tömeg jelenléte miatt. A tömeg eloszlása határozza meg a görbült teret, de ez a görbület visszahat a tömegek mozgására is. Ez az oda-vissza való hatás jelenik meg az Einstein féle gravitációs egyenletben, ami rendkívül megnehezíti a probléma matematikai kezelését és különböző elvi problémák kiinduló pontja is.
Az általános relativitáselmélet következményei
Egyszerűbb esetben, amikor a nagytömegű Nap körül vizsgáljuk a viszonylag kis tömegű bolygómozgást a megoldás jó közelítésben megadható. Einstein megvizsgálta a Merkúr pálya perihéliumának (az ellipszis pálya napközeli pontja) vándorlását, amelyet pontosabban tudott megadni, mint ami a Newton egyenletből számolható. A másik kísérleti bizonyítéknak tekintették, hogy Einstein elmélete magyarázni képes a gravitációs fényelhajlást. Ez napfogyatkozás esetén vizsgálható, amikor a Nap által eltakart csillag fénye megfigyelhető, mert az onnan érkező fotonok pályája a gravitációs térben elhajlik és így megkerüli a Napot. Ennek konkrét megfigyelése után vált Einstein elmélete általánosan elfogadottá, ami azért érdekes fordulata a fizika történetének, mert kiderült, hogy a Newton egyenlet alapján is lehet értelmezni a fényelhajlást, amelynek mértéke fele az Einstein elméletéből következő értéknek, viszont a mérési pontosság korlátai sokáig nem tették lehetővé, hogy ez alapján különbséget lehessen tenni a két elmélet között. Csak 1960-ban igazolták Pound és Rebka mérései [1], hogy tényleg az általános relativitáselmélet előrejelzése a helyes.
Einstein gravitációs egyenletének sajátságai
Kövessük Einstein egyenletének további alakulását és vizsgáljuk meg, hogy milyen elvi problémák keletkeznek ebből! A tömegek pozíciója és sebessége adja az egyenlet forrásoldalát, amit matematikailag az energia-impulzus tenzor Tab ír le, ahol az alsó index a görbült téridő koordinátáit jelöli. Ez alapján kell meghatározni a gab metrikus tenzort, ami a koordináta szorzatok együtthatója. A speciális relativitáselméletben (Minkowski téridő) gab egy négydimenziós diagonális mátrix: (1, -1,-1,-1) sajátértékekkel, ahol az első index az idődimenziónak felel meg. Ha ismerjük a görbült tér gab metrikus tenzorát, akkor ebből parciális deriválások segítségével képezhetjük az Rab görbületi tenzort, amit Ricci tenzornak nevez az irodalom. Az eredeti Einstein egyenlet:
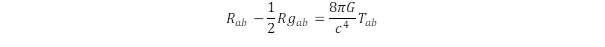
Az egyenletben G az általános gravitációs állandó és R a Ricci tenzor diagonális elemeinek összege.
A gravitációs egyenlet elvi problémái
Az elvi és a számítási nehézségek abból fakadnak, hogy a Tab tenzort az ismeretlen térgeometria koordinátáival kell kifejezni! Mintha a fizikusnak egy ismeretlen szerkezetű ingoványon kellene átkelni, ahol nem tudja, hol talál szilárd talajt. Ha egy vigyázatlan lépéskor süllyedni kezd, mozgásával megváltoztatja a szilárd és a képlékeny részek eloszlását (tehát átrendezi a tér geometriáját) és ha ráadásul ijedtében kapálózni kezd, csak meggyorsítja a süllyedést. Matematikailag ez a „rossz lépés” a kezdő feltételek rossz megválasztásának felel meg. Kijöhetnek olyan matematikai megoldások is, amelyek visszavezetnek a múltba, ami az ismert paradoxonhoz vezet: a múltban tehetnék valami olyat, ami megakadályozná saját megszületésemet, de akkor hogy mehetnék vissza a múltba, ha meg sem születtem? A nehézség valójában a gab tenzor nagy szabadsági fokából származik, mert a szimmetrikus mátrixnak 10 független eleme van, viszont a fizikai tér – az elektrodinamikához hasonlóan – csak két szabadsági fokkal rendelkezik [2].
A kozmikus állandó
Einstein megkísérelte az univerzum egészére alkalmazni egyenletét, de azt kapta, hogy az univerzum összezuhan, vagy szétszalad, ami ellenkezett koncepciójával, mert az univerzumot sztatikusnak képzelte. Emiatt kiegészítette az eredeti egyenlet bal odalát egy új taggal:λ gab, amelyben λ a kozmikus állandó. Néhány évvel később Hubble a távoli galaxisok vörös eltolódása alapján kimutatta, hogy az univerzum tágul és nincs szükség a kozmikus állandó fogalmára. Einstein azonnal elismerte tévedését és a kozmikus állandó bevezetését élete legnagyobb tévedésének nevezte. Az utókor mégis igazat adott Einsteinnek a kozmológiai állandó létezését illetően, mert a távoli szupernóva robbanások vörös eltolódása arra mutat, hogy az univerzum gyorsulva tágul, ami csak úgy értelmezhető, ha mégis szerepet játszik a kozmikus állandó.
Gravitációs lencse és az Einstein gyűrűk
Einstein kereste az analógiát az elektromágnesesség és a gravitáció között és kimutatta, hogy az optikának megfelelő effektusokat a gravitáció is okozhat extrém anyagsűrűség esetén. Szintén a gravitációs egyenletből következik, hogy nagy tömegsűrűség akkora gravitációs mezőt hozhat létre, amely már a fényt is foglyul ejtheti, ezek a fekete lyukak. Az a fény, amely elhalad a fekete lyuk mellett, erősen elhajlik és fókuszálódik, és így gravitációs lencsehatás jön létre. A lencsehatás megnyilvánulása, hogy a fekete lyuk mögötti galaxisról gyűrű alakú formációk képződnek. Ilyen gyűrűket valóban sikerült is megfigyelni igazolva Einstein hipotézisét.
A gravitációs hullám
Talán a legtöbbet vitatott és keresett jelenség, amit szintén Einstein mutatott ki a gravitációs hullám. Ez a téridő görbületének hullámszerű terjedése. A gravitációs állandó gyengesége miatt ez rendkívül gyenge hatás, maga Einstein is szkeptikus volt, hogy egyáltalán megfigyelhető-e a jelenség, de fontosnak tartotta, mert a görbült téridő létezésének egyik bizonyítékát látta benne. Két alkalommal is publikálta felvetését, mert először matematikai hibát vétett a számításban. Tévedését két évvel később aztán korrigálta. Ez is jellemzi Einstein viszonyát eredményeihez: ha valamiben tévedett azt hajlandó volt elismerni és továbblépni!
Sokan, sokféleképp akarták kimutatni a gravitációs hullámokat, mások kételkedtek benne, hogy egyáltalán létezik. Ennek oka, hogy az elektromágneses hullámokkal való analógia nem teljes. Amint arra Mayer István felhívta figyelmemet, a gravitációs mező sajátenergiája – szemben az elektromágneses mezővel [3,4] – negatív és ez lehetetlenné teszi, hogy a Minkowski féle téridőben kialakuljanak gravitációs hullámok, más szóval a gravitációs hullámok a klasszikus fizika vagy a speciális relativitáselmélet keretében nem értelmezhetők, csakis az általános relativitáselmélet ad rájuk magyarázatot. Mégis többször vélték úgy, hogy sikerült a jelenséget kimutatni, de rendre kiderült, hogy téves volt az értelmezés. Az első meggyőző bizonyítékot a LIGO kísérlet adta meg [5]. Ez azért különösen jelentős, mert ezek a hullámok a téridő görbültségének közvetlen bizonyítékai, hiszen a Minkowski téridőben nem jöhetnek létre.
A LIGO kísérlet nehézségei
A LIGO kísérlet értelmezéséhez induljunk ki a rövidítést takaró egyes szavakból: Laser Interferometer Gravitational wave Observatory. A mérés rendkívüli pontosságot igényel, mert az atommag méretével egybevethető pontosságú távolságmérésre van szükség. A másik nehézség elvi jellegű: ha maga a tér nyúlik meg, vagy rövidül, akkor ez mérési eszközünket is megváltoztatja, így a hullámokat egyetlen „mérőrúddal” nem is észlelhetjük. Viszont a tér görbül, ami avval jár együtt, hogy különböző irányokban eltérő lesz a hatása. Emiatt egy „L” alakú elrendezést kell használni és összehasonlítani a két „rúd” hosszának változását. A rudakat jó hosszúra kell választani (a LIGO-ban ez 4-4 km), mert az effektus a rúd teljes hosszával arányos. A rúd teljes hosszának változását elvileg sem láthatjuk, de mód van a két rúd hosszának különbségét követni. Ehhez kell a laser forrás és az interferométer. Az „L” alakzat közepéről sugarat kell kibocsátani mindkét irányban, majd a rúd végeken lévő tükrökkel visszavetíteni a sugarakat a találkozási pontig és ott interferenciát létrehozni. Ehhez monokromatikus és koherens sugarakra van szükség, amit a laser sugárzás biztosít. Pontos hangolással el lehet érni, hogy a két sugár épp kioltsa egymást, ezt oldja meg az interferométer. Ez a hídelv rendkívül nagy pontossággal észleli, ha a két rúd hossza eltérő mértékben változik. A mérés nagy pontossága persze veszélyforrás, mert a legkisebb külső rezgés, vagy a 4 km hosszú rúdon egy kis hőmérsékletkülönbség is hamis jeleket fog létrehozni. Emiatt szükséges, hogy legalább két távoli helyen (ez 3000 km volt) működjön két ilyen berendezés, aminek jele egyidejűleg jelentkezik, ha a változást tényleg a gravitációs hullámok okozzák. Emiatt ezer kutató munkájára és különleges elővigyázatosságra volt szükség, hogy a hamis jelek garmadájából kiválasszák a valódi effektust.
Részecskék mint a téridő fénysebességű forgásai
A sikeres mérés ismét Einsteint igazolta, de ennél fontosabb, hogy a fizika biztosan támaszkodhat a téridő görbületének elvére. Magam is ebből indultam ki, amikor a részecskéket úgy értelmeztem, mint a tér fénysebességű forgásait, ami extrém mértékű térgörbületet hoz létre [6]. A koncepció kiinduló pontja a Minkowski téridő, ezért ment azoktól a problémáktól, amelyek a makroszkopikus Einstein egyenletből származnak, ahol a görbület forrását adó energia-impulzus tenzor az ismeretlen és változó görbületű téridőben van definiálva. Mivel a részecskéket létrehozó forgások az identikus geometriára támaszkodnak így biztosítva van, hogy bárhol képződik a részecske a tulajdonságok azonosak lesznek. Az Einstein féle gravitáció másodlagos hatás, ahol a lankás görbületek rárakódnak a részecskéket alkotó éles görbületekre. Ez a koncepció elkerüli az Einstein egyenlet által megengedett szingularitást is, mert a másodlagos (gravitációs) forgás hatása nem haladhatja meg az elsődleges, fénysebességű forgásét, hiszen az annál is nagyobb centrifugális erőt már a görbült téridő nem tudná kiegyenlíteni. Ez összhangban van a Planck hossz definíciójával, ami behatárolja a fekete lyuk modellben a maximális gravitációs erőt és tömegsűrűséget [7].
A következő bejegyzésben lesz szó az EPR paradoxonról.
Ajánlott irodalom
- R. V. Pound, G. A. Rebka: „Apparent weight of photons”, Phys. Rev. Lett., 4, 337-341 (1960).
- A téma iránt érdeklődőknek ajánlom Szabados B. László kitűnő összefoglalóját (Magyar Tudomány: „Száz éves az általános relativitáselmélet). Az írás néhány gondolatát a bejegyzésben felhasználtam.
- I. Mayer: A Connection between Special Theory of Relativity and Quantum Theory”, arXiv-1207.3180v2.pdf
- P. G. Peters: „Where is the energy stored in a gravitational field”, Am. J. Phys. 49, 564 (1981).
- „Gravitational waves detected 100 years after Einstein’s prediction”, LIGO 11 February 2016.
- A. Rockenbauer: „A screw model for quantum electrodynamics: From gravitation to quanta”, INDIAN JOURNAL OF PHYSICS, 89, 389-396 (2015)
- A "Paradigmaváltás a fizikában: téridő kontra kvantumelv” című bejegyzés foglalja össze azokat az írásokat, ahol további információ található a témában.