A valószínűségtől a bizonyosságig

Mi a determinizmus 

Gondolkozásunk egyik sarokpontja a determinizmus. Úgy gondoljuk, ha pontosan ismerjük a körülményeket, akkor annak egyértelmű következménye lesz. Ezért keressük a jelenségek okát. Ezt teszi a tudomány is, így a fizika, amikor számba veszi a különböző erőhatásokat és ebből számítja ki egy test, vagy a mikrovilág valamilyen objektumának mozgását.

De honnan származik determinisztikus felfogásunk? Ennek kiindulópontja a világ megismerhetőségébe vetett hit. Ha nem lehet előre látni bizonyos előjelek alapján a következményeket, akkor nem lehetne alkalmazkodni a változó világhoz sem. Ez tehát túlélésünk egyik záloga. A determinizmus szélsőséges változata a predesztináció, amely egy sajátságos istenhitből származik. E szerint az isten előrelát mindent, ezért bármit is teszünk, az előre elrendeltetett.

De térjünk vissza a klasszikus fizika determinisztikus felfogásához annak érdekében, hogy értsük a mikrovilágban uralkodó valószínűségi koncepció eredetét. Azt a kérdést is vessük fel: vajon makro-világunk determinisztikus felfogása csorbát szenved-e a mikrovilágban, vagy épp fordítva: a mikro-folyamatok véletlen jellege alakul át többé-kevésbé determinisztikussá a mikrovilág objektumainak és folyamatainak óriási száma miatt?

Miben különbözik a labda pályája az elektronétól?

A makroszkopikus és a mikrovilág eltérő szemléletmódját érzékeltessük a labda és az elektron mozgásának összehasonlításával. Először is mit értünk azon, hogy látjuk egy teniszlabda mozgását és pályaívét? A labdáról minden pillanatban nagyszámú foton érkezik szemünkbe, vagy a felvevőgépre. De nem csak a labdáról, hanem a pályáról is érkeznek fotonok, és ez lehetővé teszi, hogy meghatározzuk a pálya koordinátarendszerében a labda pozícióját minden egyes pillanatban. Az időt is meghatározhatjuk, ha a felvevő berendezés órája is működik. Minden óra valamilyen makroszkopikus eszköz, amely egy periodikus jelenség alapján skálázza az időt. Ilyen periodikus folyamat lehet egy inga lengése, egy kristály rezgése és még hosszan sorolhatnánk. Feltételezésünk alapja, hogy a szóban forgó periódusok hossza azonos, amivel skálázhatjuk az időt. A pályafüggvény birtokában már meghatározhatjuk differenciálhányadosok képzésével a sebességet és a gyorsulást, amit Newton törvényei által kapcsolatba hozhatunk a labdára ható erőkkel. Az eljárás alapja a folytonosan érkező információ, ami alapján folytonosnak tekintjük a tér és idő koordinátáit.

A gyorsítóból kilépő elektron pályája

De vizsgálhatjuk-e hasonló módon az elektron pályáját? Ha egy elektron a gyorsítóból érkezik és áthalad az emulzión, vagy ködkamrán, nyomot hagy az ionizáció révén. Ez alapján a pálya rekonstruálható, melynek pontosságát az emulzió szemcsemérete határozhatja meg. Minél finomabb a szemcse, annál sűrűbben követhetjük az elektron nyomát, de ekkor a gyakori ütközések miatt a részecske sokat veszít kinetikus energiájából és a hozzá tartozó impulzusából. Valójában az elektron nyomának minden egyes pontja valamilyen kémiai reakció során jön létre, amelynek energia szükséglete az elektron kötési energiájának felel meg. Emiatt a nyomot analizálva korlátokba ütközünk, amikor meghatározzuk a pozíciót és az impulzust. Ennek hibája általában jóval nagyobb, mint amit a kvantummechanika szab meg a bizonytalansági elv alapján.

Elektronok stacionárius pályákon

Ezekben a kísérletekben tehát láthatóvá tudjuk tenni az elektron pályáját, de mit tudunk mondani az atomokban és molekulákban kötött pályán lévő elektronokról? Ezek az elektronok közvetlenül nem láthatók, csak amikor változás történik állapotukban és kibocsátanak, vagy elnyelnek egy fotont. Emiatt az elektronpályákról nyerhető információt a foton tulajdonságai határozzák meg!  A fotonok alaptulajdonsága, hogy a ħ redukált Planck-állandó adja meg impulzusmomentumukat, bármekkora is legyen az energia. Ezt az impulzusmomentumot jellemezzük az S = 1 spinnel. A foton olyan hullám, amelynek energiája egyúttal megmondja, hogy mekkora az impulzus és hullámhossz, és ennek a két mennyiségnek szorzata egyenlő ħ-val. Amikor a foton által határozzuk meg egy mikro-objektum pozícióját, akkor a hullámhossz korlátozza a mérés pontosságát, ezért ha növelni akarjuk a pontosságot rövidebb hullámhosszú fotont kel alkalmazni, viszont ehhez nagyobb impulzus tartozik. A mérés azt jelenti, hogy ez a foton meglöki a vizsgált objektumot és így megváltoztatja annak állapotát. Egy új méréssel már ezt a megváltozott impulzust tudjuk meghatározni, de emiatt az eredeti objektum impulzusára kapott információnk az első mérés által okozott impulzusváltozás mértékében bizonytalan lesz. Következésképp, nem lehet a pozíció és impulzus hibájának szorzata kisebb ħ értékénél. Ezt fejezi ki a kvantummechanika bizonytalansági elve. 

Mit tudunk egyáltalán mondani az elektron pályájáról, amikor nem bocsát ki, vagy nyel el fotont? A pálya időbeliségéről semmit, azaz olyan pályát nem adhatunk meg, mint amiről a labda esetén szó volt. Két fontos dolgot azonban tudunk:

• Az elnyelt, vagy kibocsátott foton diszkrét energiával rendelkezik
• Minden foton ħ egységnyi impulzusmomentumot vihet el, vagy adhat át

Ebből viszont következik, hogy az atomokban az elektron is diszkrét energiával rendelkezik és ezekhez az állapotokhoz ħ egész számú többszörösének megfelelő impulzusmomentum tartozik. A pálya időbeliségének hiánya miatt nem használható a leíráshoz a Newton egyenlet, hiszen az a gyorsulás és az erő arányosságán alapul, ráadásul a Newton törvényből számolható energia is folytonos lenne. A labda esetén elvben tudjuk, hogy egy adott pillanatban a labda hol van, az elektron esetén csak azt a kérdést tehetjük fel, hogy az elektron valószínűleg hol lehet.

Pálya a valószínűség dimenziójában

Ez a szemléletmód azt jelenti, hogy nem az idő függvényében képzeljük el a pályát, hanem csak annak valószínűségi eloszlására tudunk következtetni. Ennek értelmében a klasszikus r (t) pályafüggvény helyett valamilyen r (w) függvényt keresünk, ahol w jelöli a valószínűséget. A valószínűség azonban másképp viselkedik, mint az idő: a t idő sorba szedi az eseményeket, a w valószínűség nem; továbbá az idő távja nem korlátozott, míg a valószínűség egységre normált mennyiség. Az eltérő jelleg miatt célszerűbb a w (r) inverz függvénnyel definiálni a pályát, amelynek a teljes térre képzett integrálja az egység, ami azt fejezi ki, hogy a részecske a teljes térben biztosan megtalálható:

Ezt nevezzük a valószínűség normálási feltételének.

Mi az állapotfüggvény? 

Az elektronállapotok közötti ugrás jól meghatározott energiával rendelkező fotonokat hoz létre, amiért olyan pályákról van szó, amelyek maguk is jól definiáltak és elkülönülnek egymástól.  Ezt az elkülönültséget nem tudjuk kizárólag pozitív w függvénnyel leírni, mert az eloszlások átfedik egymást, ezért komplex számokat is megengedő állapotfüggvényre van szükség, melynek abszolút érték négyzete fejezi ki a valószínűséget:

Az elkülönültség matematikai kifejezője az ortogonalitási szabály, mely szerint a teljes térre kiterjedő integrál nulla különböző állapotok között és az egységnyi két azonos állapot esetén:

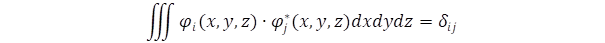
ahol δ_ij = 0, ha i ≠ j és 1, ha i = j. 

Operátorok megjelenése a kvantummechanikában

A pályafogalom átértelmezése megköveteli, hogy a többi mechanikai alapfogalom is új értelmezést kapjon. A newtoni mechanikában kulcsszerepet tölt be az energia és az impulzus. A mechanikai törvények szerint az impulzus (tehát a sebesség) nem változik meg külső erőhatás nélkül, illetve az impulzusváltozás (gyorsulás) előidézője a külső erő. Az utóbbi következménye, hogy az energiának két tagja van: a potenciális és kinetikus, és a két tag összege állandó. Ezekből a törvényekből már levezethető a klasszikus mozgási pálya. A mikrovilág állapotfüggvényei esetén viszont olyan kérdéseket kell felvetni, hogy mi alakítja ki, illetve változtatja meg a pályafüggvényeket. A függvények változtatója a matematikában az operátor, amely az egyik függvényt egy másikhoz rendeli. A térbeli változást a d/dx, d/dy, d/dz, az időbelit a d/dt differenciálhányadosok írják le. A térbeli változás az impulzushoz rendelhető, hiszen külső erő nélkül a mozgási állapot a tér bármely helyén ugyanaz. Az időbeli változatlanság megfelelője pedig az energia, amely mindaddig állandó, amíg nem alkalmazunk időtől függő erőt, azaz potenciális energiát.

Mit jelent az állandóság, amikor állapotfüggvény írja le a mozgási pályát? Azt, hogy az operátor hatására a függvény önmagába megy át. Az ilyen függvényt nevezzük az operátor sajátfüggvényének.  A függvény szerkezete nem változik meg, amikor egy konstanssal szorozzuk, hiszen ez a függvény normálásakor úgy is kiesik, viszont ez a konstans rendkívül fontos, mert azt jellemzi, hogy a szóban forgó operátornak – azaz fizikai mennyiségnek – mekkora az értéke egy adott állapotban. Ezt hívjuk sajátértéknek. 

Az exponenciális hullámfüggvény

A függvények családjából az exponenciális függvény rendelkezik avval a tulajdonsággal, hogy deriváláskor önmagába megy át: 

Ha az argumentumban „a” valós szám, akkor a függvény bizonyos x értéknél végtelen értéket vesz fel, ami azt jelentené, hogy ott a függvénynek szingularitása van. A valódi részecskemozgások valószínűségi eloszlása nem rendelkezhet szingularitással, ami úgy valósítható meg, ha kizárólag imaginárius argumentumú exponenciális függvényeket engedünk meg, amelyek térbeli és időbeli hullámokat írnak le. 

Ha fizikai mennyiséghez rendelünk operátort, akkor annak értéke csak valós szám lehet, ez megköveteli, hogy a differenciálhányadosokat megszorozzuk az „i” imaginárius egységgel. Energia illetve impulzus dimenziót, akkor kapunk a differenciálhányadosokból, ha megszorozzuk egy impulzusmomentum dimenziójú konstanssal, még pedig a ħ redukált Planck-állandóval. Ez a választás biztosítja, hogy megkapjuk a fotonok energiáját és impulzusát. A foton energiája:

Itt ω a foton körfrekvenciája. A foton impulzusa pedig:

ahol λ jelöli a hullámhosszt.

Schrödinger-egyenlet

Tehát a labda és az elektron mozgásairól nyerhető információ eltérő jellegéből kiindulva eljutottunk a kvantummechanika matematikai formalizmusához. A klasszikus mechanikával egyezően az energia két tagból tevődik össze: a kinetikus és potenciális energiából. Ezek hagyományos összefüggéseibe csak be kell helyettesíteni az operátorokat és megkapjuk a Schrödinger-egyenletet. Ha a potenciális energia nem tartalmaz időtől explicit módon függő erőhatást – ezt nevezzük stacionárius állapotnak – az energia megmarad, azaz az állapotfüggvény csak egy időtől független konstanssal szorzódik, melyet az energiaoperátor sajátértékének tekintünk. Egy kiválasztott E_n energianívó esetén a ψ_n állapotfüggvény:

ahol

Átmeneti valószínűségek

 Az időtől függő exponenciális szorzó nem befolyásolja a stacionárius pálya térbeli eloszlását, mert a komplex konjugáltjával szorzódik a valószínűségi formulában, mégis fontos a kibocsátott, vagy elnyelt foton frekvenciájának kiválasztásában. A két állapot közötti ugrás rezonanciajelenség, ahol az ugráshoz tartozó frekvencia megegyezik a foton által keltett elektromos és mágneses mező frekvenciájával. Ennek oka, hogy ezek a mezők erőhatást gyakorolnak az elektronokra és valamekkora x amplitúdójú kényszerrezgést hoznak létre az elektron pályáján. Rezonancia akkor jön létre, ha a foton ω frekvenciája megegyezik két elektronnívó különbségéből számítható frekvenciával: ω = (E_n – E_m)/ħ. Az indukált átmenet valószínűségét az határozza meg, hogy az x amplitúdójú és irányú rezgés hogyan változtatja meg a φ_m függvény térbeli eloszlását. Eredetileg a két különböző állapotfüggvény ortogonális volt egymásra, de ezt a foton által okozott perturbáció megszünteti. Az átfedési integrál négyzete adja meg, hogy mekkora az átmenet valószínűsége:

A kényszerrezgés x amplitúdója arányos az erőhatással, amit a fotonok száma határoz meg, és így az indukált átmenet intenzitása a foton szám négyzetével lesz arányos. Ha az elektron gerjesztett állapotban van, akkor külső fotonok nélkül is létrejöhet átmenet, ez a spontán ugrás jelensége, melynek valószínűsége egyetlen foton indukált hatásának felel meg. 

A valószínűség felváltása bizonyossággal a makro-világban  

Az ugrás és a foton kibocsátás, vagy elnyelés megtöri a stacionárius állapotot, azaz történik valami, és ezért szerepet kap a mérhető idő, ami például az ugrások gyakoriságával skálázható. Az idő szerepe tovább nő, amikor az elektronok kölcsönhatása molekulákká köti össze az atomokat és a molekulák is összekapaszkodnak a Van der Waals erők által. Ekkor a periodikus vegyértékrezgések, vagy a kristályok rácsrezgései már az idő dimenziójában mennek végbe és a makroszkopikus világban háttérbe szorulnak a kvantummechanika valószínűségi jelenségei. Így jutunk el fokozatosan a méretek növekedésével a klasszikus fizika bizonyosságon alapuló világába, ahol már determinisztikusok a mechanika törvényei.

A blog további írásai elérhetők: „Paradigmaváltás a fizikában”