Ha színházba megyünk és a távolról nem látjuk jól a színészek arcvonásait, segíthetünk ezen egy látcsővel, amelyen közelebb látszik a színpad, jobban láthatjuk az arcokon az érzelmek tükröződését. Ha egy tiszta éjszakán az égboltra tekintünk, és jobban akarjuk látni a csillagokat, szintén a távcső segít, felnagyítva és jobban láthatóvá téve a különböző égi objektumokat. Kicsit bonyolultabb, de hasonló dolog történik, ha felülünk egy űrhajóba, amely a fénysebesség közelébe repít minket. A kabinban semmi szokatlant nem tapasztalunk, amikor nagy sebességgel egyenletesen haladunk, nem lesz semmi sem kisebb, vagy nagyobb, a kabin tárgyai akkorák maradnak, mint induláskor, de mégis ha kinézünk az ablakon a csillagvilág képe egészen más lesz, mintha csak távcsőbe néznénk. Pillantsunk előre és azt látjuk, hogy az előttünk lévő csillagok sokkal közelebb kerülnek hozzánk, de nézzünk hátrafelé is, bár távolodunk, mégis az égi objektumok közelebb látszanak, mint indulásunk előtt. Ugyanakkor jelentősen különbözik ez a látvány a szokásostól, mert megváltoztatja a színeket, előttünk minden kékebbnek, mögöttünk minden vörösebbnek látszik. Továbbá, ha mellettünk robog egy másik űrhajó a miénkkel azonos sebességgel, annak nagyságában, távolságában és színében nem veszünk észre semmi változást, oldalirányban az űrhajó sebessége nem változtatja meg a látható világot. Van azonban egy még szokatlanabb dolog, egy olyan változás, amit az űrhajóban észre sem veszünk: lelassul óránk sebessége. De nem csak óránk fog ritkábban tiktakolni, életritmusunk is lelassul, így nem is gondolunk rá, hogy lassabban telik az idő. Csak abból derül ki az idő lassulása, hogy saját naptárunk szerint hamarabb érjük el célba vett csillagot, mint amire akár a fénysebesség is képes lenne. Viszont amikor a lassuló óra méri az időt, és hozzá hasonlítjuk az űrhajóból látható rövidebb távolságot, a fénysebesség értéke nem különbözik attól, amit a Földön is meghatározhatunk. Tehát a távolság rövidül, az idő lassabban telik, de a fénysebesség mégis állandó marad. Van még egy további észrevehetetlen változás is: ahogyan csökken a hosszúság, úgy növekszik meg a tömeg, de ezt se érzékeljük, mert a mérés alapjául szolgáló tömegegység is ugyanúgy nagyobb lesz. Persze ezek a szokatlan jelenségek a Földtől való távolodás nagy sebességénél lesznek jelentősek. Alapul véve a fény 300 000 km/s sebességét, ha űrhajónk ennek 99,5 százalékával távolodik, azaz másodpercenként 298 500 kilométert tesz meg, akkor már 10-szeres a változások mértéke a relativitáselmélet Lorentz-kontrakciós szabálya szerint, amit a γ paraméter fejez ki:
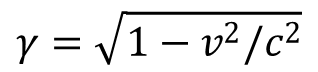
A müonok meghosszabbodott élete
Arra nincs igazán esély, hogy ekkora sebességre felgyorsítsuk űrhajónkat a hatalmas energiaigény miatt, de megvalósul a felső sztratoszférából érkező müonok esetén, melyeket a kozmikus sugárzás nagy energiájú protonjai hoznak létre, amikor ütköznek nagy magasságban a levegő molekuláival. A müonok példája azért érdekes, mert életük rövidre szabott, amikor a földi laboratóriumban képződnek élettartamuk (felezési idejük) 2,2 μs. Ez azt jelenti, hogy ennyi idő alatt számuk már felére csökken, és ez a feleződés exponenciálisan folytatódik. Ezek a részecskék 15 km magasságban jönnek létre, ahonnan még a fénynek is 50 μs időre van szüksége, hogy a Föld felszínére jusson. Azt várnánk tehát, hogy a földi laboratóriumokban alig figyelhetnénk meg müonokat. Összevetve azonban a sztratoszférában képződő müonok számát a felszínen megfigyelt mennyiséggel, a mérések azt mutatják, hogy a száguldó müonok élettartama tízszer hosszabb lett. Ezt persze mi mondjuk saját koordináta rendszerükben, a müonok viszont úgy „érzik”, hogy továbbra is 2,2 μs alatt feleződnek, csakhogy nekik 1,5 km volt a megtett útjuk a Lorentz-kontrakció miatt, és ehhez elég volt számukra 5 μs idő.
Az ikerparadoxon
Kétféle rendszerben gondolkozhatunk, a sajátunkban itt a földön állva, de gondolkozhatunk a müon száguldó rendszerében is. Mind a kettő ekvivalens inerciarendszer a relativitáselmélet szerint, érvényesül benne a fénysebesség állandósági szabálya, és ehhez kapcsolódóan azonos marad benne minden fizikai törvény. Mégis zavarba jövünk, amikor az ikerparadoxonról beszélünk. Az ikerparadoxon akkor lép fel, ha összekötjük az inerciarendszereket. Az ikrek egyike itt marad a Földön, a másik űrutazásban vesz részt. Az egyszerűség kedvéért ne foglalkozzunk avval a szakasszal, amíg felgyorsul az űrhajó, és nézzük csak azt, amikor az űrhajó már nagy sebességgel egyenletesen halad, azaz jogosan beszélünk inerciarendszerről. Ezt az indokolja, hogy az elvégzett kísérletek szerint nem számít a müon élettartama szempontjából, hogy mekkora volt a gyorsulás, amikor laboratóriumokban gyorsították fel a müonokat. Célszerű egyébként az űrhajó gyorsulását a földi 1 g = 9,83 m/s2 értékűnek venni, mert ekkor az űrhajósokra a földi gravitációnak megfelelő erő fog nehezedni a hosszú út során. Kisebb gyorsulás persze hosszabb idő alatt fogja felgyorsítani az űrhajót, ami hozzájárul az ikrek korának eltéréséhez is, de most koncentráljunk arra a szakaszra, amikor már kikapcsoltuk a sugárhajtást, és az űrhajó sebessége nem változik. Ha innen számolva az űrhajó egy 10 fényévnyi körutat az 5 fényév távolságban lévő csillagig γ= 10 Lorentz-faktornak megfelelő sebességgel tesz meg, akkor ez számára csak 1 évet vesz igénybe. A földi ikerhez képest így az űrutas 9 évet nyert, ami már érzékelhető korkülönbség az ikrek között.
Miért beszélünk paradoxonról? Ezt a két inerciarendszer ekvivalencia szabálya okozza! Az otthon maradó iker szemszögéből nézve, a hozzá képest nagy sebességgel (azaz nagy γ értékkel) halad, így hazatérve fiatalabb lesz nála. De hogy néz ki a helyzet az utazó iker rendszeréből nézve? Ő is a saját rendszeréhez hasonlítja az ikertestvér sebességét, hiszen a relativitás elve miatt nincs abszolút sebesség, csak az számít, hogy mekkora a különbség a két inerciarendszer sebessége között. Ez a sebesség ugyan fordított irányú, azaz negatív, de mivel a sebesség előjele közömbös a γ Lorentz-kontrakció számításánál, így az űrutas azt gondolhatná, hogy a földön maradó ikertestvér órája lassul le tízedére, tehát a találkozáskor a másik lesz fiatalabb. Az ellentmondás a két gondolkozás között nyilvánvaló!
Van-e abszolút referencia rendszer?
Kinek van igaza, melyik állandó sebességű inerciarendszer alapján kell számolni? Talán mégis lenne egy abszolút vonatkoztatási rendszer, ami alapul szolgálhat az űrhajó sebessége szempontjából?
Ha elfogadjuk a Lorentz-szabály érvényességét, csak arra gondolhatunk, hogy a két inerciarendszer mégsem ekvivalens: a számítás csak az egyik inerciarendszerben ad helyes eredményt. De milyen alapon választjuk ki a helyes rendszert? A szokásos magyarázat a gyorsulásra hivatkozik, mondván az utazó iker gyorsult és lassult, míg a másik helyben maradt, és az aszimmetrikus előélet okozza a különbséget. Ezt magyarázza hosszasan a wikipedia angol nyelvű cikke is, ahol olyan számításokat végeznek el, amiben csak a gyorsulásról és lassulásról esik szó, és nem tárgyalják az állandó sebességű szakaszt. De ha a gyorsulás-lassulás a lényeg, akkor miért jön létre korkülönbség az egyenletes sebességű szakaszban is, mégpedig arányosan avval, hogy milyen hosszú ideig volt a két rendszer sebessége különböző? A müonnal elvégzett laboratóriumi kísérletek, ahol óriási gyorsulást alkalmaztak, szintén arra mutat, hogy nem számít a tényleges gyorsulás nagysága.
Az impulzusmegmaradás kulcsszerepe
A helyes választ segít megtalálni az impulzusmegmaradás törvénye, ami egyúttal kapcsolódik a minimális mozgási energia megtalálásához is. Az űrhajó indulása előtt a földi rendszer része volt, és jelöljük a Föld és az űrhajó tömegét „M” és „m” betűkkel. A kilövés után megadhatjuk az űrhajó „v” sebességét a Földhöz képest, vagy fordítva, a Föld „V” sebessége „-v” lesz, ha az űrhajó sebességét vesszük nullának. A józanész az előbbit tartja helyesnek, és igaza van, ha a nagyságrendet tekintjük alapnak, hiszen az űrhajó tömege elhanyagolható a Földhöz képest. Ha nagyon precízek vagyunk, persze bevezethetjük a súlyponti rendszert. Ebben az impulzus összege nulla lesz, vagyis m·v = ̶M·V. Ha nem a súlyponti rendszert veszem alapul megszegem az impulzusmegmaradási törvényt, ezért a törvény megtartása már kijelöli a helyes vonatkoztatási rendszert, amelyik persze gyakorlatilag egyezik a Földével. A reális sebesség az energia abszolút nagyságának kiszámítása miatt fontos. A kinetikus energia a sebesség négyzetével arányos, emiatt bár a Föld és az űrhajó impulzusa egyenlő a kilövés után, a Föld mozgási energiája elhanyagolható az űrhajóhoz képest. A Földhöz viszonyított rendszer kitüntetett szerepe megmarad akkor is, ha rakétákkal, vagy sugárhajtó művel tovább gyorsítjuk az űrhajót. Nagy sebességeknél már a relativitáselmélet kovariancia elve szerint kell számolni az energiát, amely figyelembe veszi az m0 nyugalmi tömeghez tartozó E0 = m0c2 energiát is. A kovariancia törvény szerint:
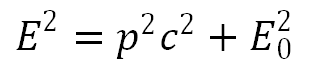
Itt p = m·v az impulzus. Figyelembe véve a tömeg-energia ekvivalencia törvényt, amely szerint E = mc2, azt kapjuk, hogy a mozgás által megnövelt energia arányát a nyugalmi energiához képest, szintén a Lorentz-faktor adja meg:
E = E0/γ
Az energia és idő kapcsolata
Az energiának kulcsszerepe van az óra lassulásának számításában. Planck felismerése szerint a fotonok energiája a frekvenciával arányos, ami úgy is megfogalmazható, hogy az energia a hullám T periódus idejével fordítottan arányos:
E = h·f = h/T
A kvantummechanika felismerése, hogy valamennyi részecske rendelkezik hullámtermészettel, amiért az E·T = h szabály érvényes a mikrovilág valamennyi objektumára és az ezekből felépülő makro objektumokra is. Legyen szó akár a parányi müonról, vagy az űrhajóról, az objektum „v” sebessége határozza meg a periódus idő növekedését a Lorentz-faktoron keresztül:
T = γT0
Ez az óra lassulásának törvénye, amit szokás az idő dilatációjának is nevezni. A törvényből az is következik, hogy a fény sebessége az űrhajó rendszerében is ugyanakkora, hiszen a fény által megtett út is ebben az arányban csökken. A Lorentz-faktorban a sebesség nagysága attól függ, hogy melyik inerciarendszer a viszonyítás alapja. Ha minden inerciarendszer ekvivalens, akkor az idő dilatációja csak látszólagos jelenség, ez csak akkor válik valóságossá, ha van valamilyen fizikai ok, ami megkülönbözteti a referencia rendszert az összes többitől. Ilyen fizikai ok, ha a vizsgált fizikai objektum egy nagyobb rendszer része volt, és az onnan való kilépés energia befektetéssel jár együtt. Ekkor az elkülönített rendszer szempontjából az induló rendszer tömeg középpontja már kitüntetett szerepet játszik, és ehhez viszonyítva az idő dilatáció látszólagossága már mérhető fizikai mennyiséggé válik.
Idő dilatáció gravitációs mezőben
Az idő dilatáció másik formája, amikor az óra lelassul gravitációs erőmezőben, ennek szabályát az általános relativitáselmélet alapján adja meg a szakmai irodalom. Ha azonban eltekintünk az extrém erős gravitációs mezőtől, hasonló eredményre juthatunk Newton gravitációs törvényből is. Fogadjuk el azt az alapelvet, hogy
bármilyen energianövelő folyamat idő dilatációt okoz, amelynek mértékét a nyugalmi energiához viszonyított teljes energia határozza meg a γ = E0/E összefüggés szerint.
Evvel kiterjesztjük a Lorentz-faktor fogalmát más jelenségekre is, amely nem kötődik ahhoz, hogy milyen tagok járulnak hozzá az energiához, így ez vonatkozik a potenciális energiára is. Ennek egyik formája a gravitációs energia V = GMm/R. Vonzó erő esetén a potenciális energia negatív, taszítás esetén pozitív, ami a gyorsulás iránya szempontjából fontos, de nem befolyásolja, hogy mekkora a sebesség négyzetének, azaz a kinetikus energiának változása. Emiatt a gravitáció energia megnöveli az E0 nyugalmi energiát az effektív Lorentz-faktor számításánál:
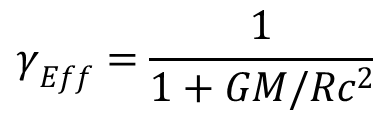
A formulában szerepel az általános gravitációs állandó G = 6,673·10-11 m3/kg·s2, a Föld tömege M = 5,9722·1024 kg, valamint a sugara R = 6371 km.
A Hafele-Keating kísérlet
1971-ben egy fizikus és egy csillagász, mégpedig Joseph C. Hafele és Richard Keating, gondoltak egy nagyot, és atomórákkal zsebükben útra keltek, hogy ellenőrizzék a speciális és általános relativitáselméletet az idő dilatáció kimutatásával. Először kelet felé, majd nyugat felé repülték körbe a Földet, majd a körút végén összehasonlították az utazó órákat az otthon letétbe helyezett masinákkal. Az összehasonlítás eredménye az lett, hogy kelet felé haladva az óra 59 ns késést, nyugat felé 273 ns sietést szedett össze.
Végezzünk becslést, hogy lássuk a nagyságrendeket! Ehhez alapul lehet venni, hogy a gépek átlagban 1000 km/óra sebességgel repültek és az átlagos magasság 10 km volt. Ez azt jelenti, hogy a földön hagyott óra R értéke a Föld középpontjától számítva 6371 km, amely megnőtt 6381 kilométerre a repülés során. Ekkor az utazó és a földön maradt órák γEff faktorainak különbsége 1,089·10-12. Ha Washington magasságában körbe utazzuk a Földet, akkor 33 000 kilométert kell megtenni, ami 1000 km/óra sebesség esetén 33 nettó óra alatt tehető meg. Természetesen az utazási idő és távolság hosszabb a menetrend szerinti légi járatokon, mert azok pályája nem pontosan követi a kelet-nyugati irányt. Vizsgáljuk meg a két kísérletező által megadott adatokat! Az általános relativitáselmélet alapján kiszámították, hogy kelet felé utazás során 144 ns, nyugat felé 179 ns sietés lenne várható, a különbség főleg az utazás eltérő idejéből származik. Felhasználva a γEff dilatációs faktorok előbb megadott különbségét, egyezést kapunk Hafele-Keating számításával, ha a kísérletezők effektív utazási ideje 36,7, illetve 45,7 óra volt. Az így becsült utazási idők reális hossza arra utal, hogy a Newton formulára alapozott effektív Lorentz-faktor akkora értéket ad az idő dilatációra, mint az általános relativitáselmélet.
Az idő dilatáció másik összetevőjét a repülőgépek sebességéből kell kiszámítani. Itt az alapkérdés, hogy mihez kell viszonyítani a repülő sebességét, a Földhöz, a Naphoz, esetleg az egész Tejúthoz, netán valamilyen éterhez?
Amikor a szokásos módon beszélünk a repülők sebességéről, azt a Földhöz viszonyítjuk. Ha ez alapján számítjuk ki a Lorentz-faktort, nem tudjuk megmagyarázni, hogy miért siet az atomóra, ha nyugat felé haladunk, és miért késik kelet felé. Tehát a Föld forgását is számításba kell venni! De ha már a Föld forgási iránya szóba jön, válaszolni kell a kérdésre, hogy a Föld mihez képest forog? A kopernikuszi válasz után nem lehet kétséges, hogy nem a Nap kering a Föld körül, hanem a Föld forog saját tengelye körül. A Nap-Föld rendszer teljes mozgási energiájának számításánál reális értéket akkor kapunk, ha a Naphoz viszonyítjuk a sebességeket az égitest óriási tömege miatt. Persze a pontos számítás a súlyponti rendszerből végezhető el, de nem követünk el nagy hibát, ha maradunk a Naphoz kötött koordinátáknál. A repülő nem szakad ki a Föld vonzáskörzetéből, hanem együtt halad vele, ezért a Nap forgása és égi útja a Tejútban nem játszik szerepet. Más lenne a helyzet egy olyan kísérletben, ahol már Nap körüli pályákat hasonlítanánk össze, ahol a Nap tengelyforgási irányával egyező és az avval ellentétes pályán mozgó órák idő dilatációját vetnénk össze. Ekkor már nem kerülhetnénk meg a kérdést, hogy mihez képest forog a Nap, és valamilyen galaktikához kötött inerciarendszerben kapnánk a helyes eredményt.
De maradjunk itt a földön! A Föld körberepülése nagyjából a 38 szélességi fok körül történt a 33 000 km hosszú délkörön, ahol a földforgás kerületi sebessége 1380 km/óra, ehhez kell a repülő Naphoz képesti sebességét viszonyítani, ami 380 km/óra nyugat felé és 2380 km/óra kelet felé. Hasonlítsuk össze a Lorentz-faktorokat, amikor kelet, illetve nyugat felé halad a gép levonva ebből a Föld felszínén tartott órára vonatkozó értéket. A különbség nyugat felé 0,7545·10-12 (az óra siet), kelet felé ̶1,612·10-12 (az óra késik) lesz. Szorozzuk meg ezeket a különbségeket a 33 órás névleges idővel, ekkor kelet felé 90 ns sietést, kelet felé -192 ns késést kapunk. Az így becsült értékek közel vannak a Hafele és Keating részletes számításának eredményével, amely 96 ns és -184 ns volt. Úgyszintén a gravitációs és kinematikai járulékok összege jól reprodukálja az atomórák által szolgáltatott adatokat. Megállapíthatjuk, hogy az a referencia rendszer, amelyet a Naphoz kötünk, jól magyarázza a mért idő dilatációt. Másképp fogalmazva, az idő dilatációjának mérésével megtalálhatjuk a súlyponti rendszert, amelyben a mozgási energia összege minimális.
A gyorsulás és gravitáció ekvivalenciája
Az általános relativitáselmélet kiindulópontja, hogy a gyorsuló rendszerben fellépő tehetetlenségi erő nem különböztethető meg a gravitációtól, ez az Einstein által megfogalmazott ekvivalencia tétel. Ha ez így van, akkor ebből az következik, hogy a gyorsulás együtt jár az idő dilatációjával. Nézzük meg ennek mértékét a fénysebességtől távoli tartományban! A Newton egyenlet szerint az erő a tömeg és a gyorsulás szorzata: F = m·a. Az erővel szemben végzett munkavégzés hozza létre az energianövekedést: ΔE = F·s, ahol az adott közelítésben s = ½a·t2, ha álló helyzetből indulunk. Az így számítható energia a mozgási energiának felel meg: ΔE = ½m·a2t2 = ½m·v2. Ezt a növekményt figyelembe véve az effektív Lorentz-faktor:
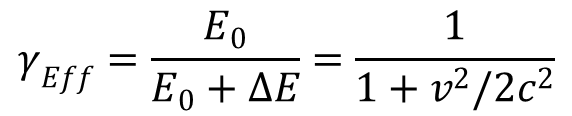
Kis sebességeknél ez pontosan megfelel a szokásos Lorentz-faktornak. Ez azt mutatja, hogy az idő dilatáció kizárólag az elért sebességtől függ bármekkora is legyen a gyorsulás. A gyorsulásnak csak abban van szerepe, hogy mennyi idő alatt érünk el valamekkora sebességet. Más szóval a gravitációval ekvivalens gyorsulás nem hoz létre többleteffektust, ahhoz képest, amit a speciális relativitáselmélet már megadott. Ha azonban összehasonlítjuk az idő dilatációját eltérő nagyságú gravitációs mezőben (például az egyik óra legyen geostacionárius pályán, a másik pedig a földön), akkor az órák sebessége eltérő lesz. A Föld körül keringő műholdak esetén a centrifugális erő kiegyenlítő hatása hozza létre a súlytalanságot, a földön állva egy felfelé ható kényszererő akadályozza meg a szabadesést. Sem a centrifugális erő, sem a kényszererő nem játszik szerepet az objektum energiájában, mert nem hoznak létre elmozdulást a külső erő irányában, azt csak kiegyenlítik. Energianövelő hatás nélkül pedig nem járulnak hozzá az idő dilatációjához sem.
Az energiamérleg szerepe
A Hafele-Keating kísérletből nyert tapasztalatok alapján könnyebben megérthetjük az ikerparadoxont is. Az alap a szétválasztás, amikor az egységes rendszer egy része külön válik elrugaszkodva onnan. Ez történik a müon útra indulásakor is, mert a földi rendszerhez tartozó levegőmolekula kap egy nagy lökést a kozmikus sugárzás protonjaitól, amely energiája révén kiemeli ezt a részecskét a Földhöz kötött inerciarendszerből. Ez a mozgási energia nyereség lesz a forrása a meghosszabbodott felezési időnek. Az űrhajó is leválik a földi rendszerről, amikor óriási energia befektetés árán útnak indul és gyorsítja sebességét. Mindkét esetben a nagyrendszer tényleges (nem csak elképzelt!) energiát ad át a részrendszernek, amelynek ezáltal sokszorosan megnő az energiája az eredeti m0c2 nyugalmi energiához képest. A lényeg tehát az energiamérleg! Ez dönti el, vajon a müon, illetve a száguldó űrhajó rendszerét kell-e alapul venni a számításokban, vagy a földi rendszert. Ha az űrhajó rendszeréhez viszonyítjuk saját sebességünket, azt nullának vesszük, amihez nem tartozik kinetikus energia. Viszont ebben a rendszerben a Föld fog közel fénysebességgel mozogni, melynek kiszámítva kinetikus energiáját óriási értéket kapunk. De ez csak számítás, csak fikció, hiszen mitől nőtt volna meg a Föld mozgási energiája? Az energiacsere iránya nem válaszható meg önkényesen, nagyon is valóságosan kell befektetnünk rengeteg energiát a gyorsításhoz. Szintén valóságos folyamat, ahogy a kozmikus sugárzás protonja átalakítja a levegőmolekulát, és nagy sebességet ad a kirepülő müonnak. Az inerciarendszereket az energiaátadás iránya különböztet meg. Az ekvivalencia csak egy matematikai, transzformációs szabály, amely kimondja, hogy a leírás szempontjából nincs különbség a két inerciarendszer között, mindkettőben azonosak fizikai törvényeink, de ez csak addig igaz, amíg nem teremtünk valóságos kapcsolatot a két különböző sebességű rendszer között, amíg nem gondolunk arra, hogy honnan is származik a mozgó rendszer energiája. Általánosságban ugyan nem létezik kitüntetett referencia rendszer, de ha energia befektetéssel létrehozunk egy új rendszert, annak számára az induló rendszer kitüntetett lesz.
Amikor az ikertestvér visszatér a hosszú útról, elveszíti a korábban felvett mozgási energiát, hiszen a Földhöz képest ekkor már nem mozog. Az ikrek közötti korkülönbség fejezi ki a rendszer „emlékezetét” arra a körülményre, hogy a felgyorsított rendszer milyen hosszú ideig volt energiával feltöltött állapotban az induló rendszerhez viszonyítva.
Visszatérés a múltba
A legfontosabb megállapítás, hogy a matematikai ekvivalencia nem jelent egyúttal fizikai egyenértékűséget is, ennek hiánya viszont csak tényleges összehasonlításkor derül ki. A dilemma oka, hogy a Lorentz-kontrakció a sebesség négyzetével arányos. Ehhez kapcsolódik az idő irányának megfordítása is. Ha visszamennénk a múltba, a sebesség előjele megfordulna, de a négyzete azonos marad. Emiatt ugyan az időben előre, vagy visszafelé haladás matematikailag ekvivalens művelet, az idő iránya mégsem fordítható meg, amit a fizika a termodinamikai entrópia törvényével magyaráz. Az idő megfordíthatatlansága tükröződik az ikerparadoxonban is: fiatalabbak nem lehetünk, csak kevésbé idősek. Nem irigyelhetjük az űrutast azért sem, mert bár naptári években számolva tovább élhet, de a hosszú út alatt megtakarított idő egyúttal kevesebb élményt is jelent.
Összefoglalás
Az inerciarendszerek ekvivalenciája a relativitáselméletben azokra a megfigyelésekre korlátozódik, amelyekben a fotonok frekvenciája az alap. A frekvenciát két állapot energiakülönbsége szabja meg, amit nem befolyásol az energia nullapontjának megválasztása. Az idő dilatáció mérése viszont új lehetőséget nyit meg, mert ez már az energiaarányokról nyújt felvilágosítást. Az arány alapja az m0c2 nyugalmi energiához való viszonyítás. Ekkor az energia nullapontja nem választható meg önkényesen, mert evvel felborítanánk az arányokat. Eltérő sebességű rendszerekben az idő dilatáció, a tér kontrakció, vagy a tömegnövekedés csak látszólagos jelenségek, mindaddig, amíg nem teremtünk valódi fizikai kapcsolatot két inerciarendszer között. Ha viszont energia befektetés árán szétválasztjuk, majd összekötjük az inerciarendszereket, már átformálódik a látszatok relativisztikus világa, a látszatból valóság lesz!
Az idő dilatáció jelensége az energiához kapcsolódik, és nem korlátozódik a mozgási és gravitációs energiára, nem indokolja ezért semmi sem, hogy ne lépne fel más erőmezőben is. Megérné ennek kísérletileg utánanézni, elektromágneses mezőben megfigyelve rövid élettartamú részecskék, vagy radioaktív izotópok felezési idejét. Ilyen lehetne a szén C-11-es izotópja, amelynek felezési ideje 20 perc és ennek értéke egy ezrelék pontossággal ismert. Ez a határ már elérhető, ha a C-11 atommagokat 2 millió voltos elektromos térbe helyezzük el.
A blog további írásai: Paradigmaváltás a fizikában