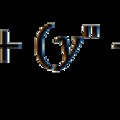A fizikai világ két arca: A látható és a láthatatlan

Fizikai világunknak két arca van, az egyik látható, a másik láthatatlan. Az egyik világ fotonok, azaz a fény által küldi el hozzánk az üzenetét, ezért látható, a másik háttérben marad, de jelenléte szükséges, hogy a látható világ létrejöjjön és fenn maradjon.

Einstein felfedezi a láthatatlan világot

Ezt a második világot Einstein fedezte fel, amikor a gravitációt a tér torzulásával magyarázta. Ahol tömeg van, ott nem lehet leírni a teret egyenes koordinátákkal, ott görbül a tér, amely vezérli a tömegek mozgását, ami letér az egyenes útról, hogy kövesse a tér görbületét. Ezt érzékeljük gravitációnak. Ez a görbült tér még a fotonok útját is eltéríti. A görbült tér világa a láthatatlan, második világ.

Honnan származik a tömeg?

De honnan származik a tömeg és miért kapcsolódik össze a tömeg és az energia az E = m.c² összefüggés szerint? Vajon a tér csak passzívan begörbül a tömeg hatására, vagy lehet szerepe a tömeg létrehozásában is? Erre a kérdésre keresve a választ jutottam el a fénysebességű forgás koncepciójáig. A foton is fénysebességű forgás, de emellett még terjed is ezzel a sebességgel. A két fénysebességű mozgás együttese teremti meg a foton mozgási tömegét, de nyugalmi tömegről nem beszélhetünk, mert a foton sorsa, hogy nem lehet nyugalomban. A nyugalomhoz az kell, hogy a részecske valahol legyen és ezt a lehetőséget két fénysebességű forgás összekapcsolódása teremti meg. Így jönnek létre a nyugalmi tömeggel rendelkező részecskék, az elektron és társai a különböző fermionok.

Forgómozgás és a tér görbülete

Minden forgás torzítja a teret a Lorentz kontrakció miatt, ami csak a mozgás irányában hoz létre rövidülést. Emiatt a körmozgás kerülete rövidebb lesz, aminek mértékét a kerületi sebesség aránya szabja meg a fénysebességhez képest, miközben a keringés sugara nem változik. A bolygómozgás Kepler törvényei szerint a keringés sebessége csökken a Naptól való távolsággal, a kerületi sebesség négyzete a sugárral fordítva arányos. Ebből adódik, hogy a tér görbülete a sugár négyzetével csökkenni fog, azaz a gravitáció mértéke is ebben az arányban csökken.  A gravitációs keringés centrifugális erejét tehát a tér görbületéből fakadó centripetális erő egyenlíti ki. (lásd erről részletesen: „Fénysebességű forgások és a relativitáselmélet”.) Megfogalmazhatjuk a kérdést az energia nyelvén is: a keringés kinetikus energiáját kiegyenlíti a görbült tér potenciális energiája. Más szóval a láthatatlan és a látható világ energiája együtt nulla lesz. A keringő mozgáshoz tehát nem energia kell, hanem a kezdő lökés: az impulzus, amely útjára indítja a keringést.

A fénysebességű forgás koncepciója

De mi a helyzet a fénysebességű forgással? Ekkor a kerületi sebesség adott, csak egy dolog változhat, a keringés ν frekvenciája, hiszen  c = 2πr.ν. A keringési frekvencia kijelöli ezért a sugarat is, amely r = c/(2πr.ν) lesz, azaz a sugár annál kisebb, minél nagyobb a frekvencia. A fénysebességű forgás nullára csökkenti a kerület hosszát és így létrehozza a maximális görbületet és ez a maximális görbület az r sugárra vonatkozik, és minél rövidebb a sugár, annak mértékében növekszik a görbület is. Itt is alkalmazva a gravitáció esetén talált összefüggést a potenciális energia és a görbület között jutunk el, ahhoz a felismeréshez, hogy a fénysebességű forgás által görbült tér potenciális energiája –m.c² lesz, ami pontosan kiegyenlíti az m.c² nyugalmi energiát, ami voltaképp a részecske sajátforgásához tartozó relativisztikus kinetikus energia. (A relativitáselmélet következménye, hogy a kinetikus energiából elmarad a nem-relativisztikus mechanikában megszokott ½ tényező).

Éles és lankás görbületek a térben

Evvel kiegészült képünk a második, a láthatatlan világról, amelyben a gravitációt leíró lankás görbület mellett fellépnek a részecskék forgását stabilizáló éles tüskék is. Most már a tér nem csak elszenvedi a tömeg torzító hatását, hanem a tömeg forrása is. Ezek a görbületi tüskék rendkívül élesek, mert a fénysebességű forgás ereje, amit erős gravitációnak nevezhetünk, akár negyven nagyságrenddel haladhatja meg a szokásos gravitációét.

A görbült tér szemléltetése

A fenti elvont gondolatokat tegyük szemléletessé egy hasonlattal. Képzeljünk magunk elé, egy hajót, amelyik úszik a tengeren. A hajó nem süllyed el, mert fenntartja a víz felhajtó ereje. Archimédesz törvénye szerint, annyi vizet szorít ki, aminek súlya egyezik a hajóéval. Minél nehezebb a hajó, annál nagyobb lesz a vízben a bemélyedés, azaz a víz görbülete. Ebben hasonlít a részecskéhez, amelynek sajátforgásához tartozó centrifugális erejét a tér görbületéből származó erőhatás egyenlíti ki. Mi is ott vagyunk a hajón és felveszünk egy olyan szemüveget, amellyel nem látjuk magát a hajót, az egyébként látható világ objektumát, viszont képesek vagyunk látni a tengert. Ekkor látunk egy bemélyedést magunk alatt, de azt is látjuk, hogy a hajó közelében a víz kissé belapul. ha ide kerül egy apró tárgy az úgy viselkedik, mintha a hajó magához vonzaná. Ez a kis belapulás felel meg a tömeg körül kialakuló torzulásnak, ami a gravitációhoz vezet.

Tehetetlen tömeg: a tér közegellenállása

A hajó mozgását úgy tudjuk biztosítani, ha működik a motor, mert le kell küzdeni a víz közegellenállását. Ebben a hajó mozgása különbözik a mechanikai tömeg mozgásától, amelyik megtartja egyenes vonalú egyenletes mozgását, ha nem hat rá külső erő, így súrlódás, vagy közegellenállás. A víz helyzete pozícióhoz kötött, ha nincsenek áramlatok és eltekintünk a molekulák véletlen mozgásaitól, emiatt lehet a víz viszonyítási alap, amelyhez a hajó sebességét hasonlíthatjuk. Más a helyzet a térben, amely nem ad abszolút viszonyítási pontokat és csak arra van lehetőség, hogy a különböző testek egymáshoz képesti pozícióját és sebességét megadjuk. Ha csak egyetlen fizikai objektumról van szó, amelyik nincs más objektumok gravitációs mezejében, akkor sem a pozíciónak, sem a sebességnek nincs értelme és így sebességfüggő közegellenállásról sem beszélhetünk.

A továbbiakban képzeljük el, hogy hajónk ebben a térben úszik. Kapcsoljuk be a motort, amely felgyorsítja a hajót. A gyorsulás ekkor kijelöl egy irányt és a sebesség változását is megfigyelhetjük a tehetetlenségi erő miatt. Az általános relativitáselmélet ekvivalenciát állít fel a gravitációs erő és a tehetetlenségi erő között, azaz a gyorsulás ekvivalens avval, mintha egy másik test gravitációs mezejébe került volna a hajónk. A térgörbület szempontjából ez úgy jelentkezik, mintha a hajó előtt létrejött volna egy kisebb bemélyedés, ami húzóerőt gyakorol. A hajó tömege, azaz a hajót fenntartó bemélyedés nagysága határozza meg, hogy mekkora a hajtó erő, ami a gyorsulást létrehozza. A gyorsulás szempontjából tehát a térnek van közegellenállása, ami arra vezethető vissza, hogy a gyorsulás az ismeretlen, illetve értelmezhetetlen alapsebesség ellenére is mérhető tulajdonsága a fizikai objektumoknak. Másként fogalmazva, a tehetetlenség a tér ellenállása, hogy a benne levő térgörbületeket gyorsítva rendezzük át. és minél élesebb a térgörbület, annál nagyobb erő kell a gyorsuló átrendezéshez.

A tömeg sebességfüggése

De mi a helyzet két objektum (hajó) esetén? Ekkor értelmet nyer az objektumok egymáshoz képesti sebessége, és ez mutatkozik meg a speciális relativitáselmélet sebességfüggő tömeg fogalmában is: a relatív sebesség fénysebességhez viszonyított nagysága határozza meg a tömegnövekedés mértékét! Ez úgy mutatkozik meg az egyik hajóról nézve, hogy egyaránt növekszik a sebességgel a másik hajó alatt megfigyelhető éles és az előtte lévő lankás bemélyedés.

Látható-e a láthatatlan világ?

Van-e olyan kölcsönhatás, amelyik a láthatatlan világot láthatóvá teheti? A válasz az, hogy van, és ez a gyenge kölcsönhatás. Az elektromágneses kölcsönhatás közvetítője a foton, segítségükkel láthatjuk az egyik világot, a gyenge kölcsönhatást közvetítik a W és Z bozonok. Ezek azonban rendkívül rövid élettartamú és nagy tömegű részecskék, amelyek töltéssel is rendelkezhetnek. Ezek a részecskék adnak hírt a görbült tér világáról, mert például a neutron alfa bomlásakor létrejönnek és átrendezik a tér görbületeket. A gyenge kölcsönhatás bozonja a proton és neutron tömegének közel százszorosával rendelkezik. Létrejöttük titka, hogy a görbült tér és a látható világ összes energiája állandó marad, hiszen amennyivel nő a látható világ energiája, azt kompenzálja a görbült tér potenciális energiája és így nem sérül az energiamegmaradás törvénye.

A blog egyéb írásait összefoglalja és megadja a linkeket a „Paradigmaváltás a fizikában” című bejegyzés.