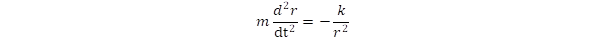A fizikai valóság keresése a matematikai formulák mögött
A fizikának szüksége van matematikára, mert csak így tudja kvantitatív módon megfogalmazni törvényeit. De ugyanakkor ennek bonyolult formalizmusa elidegenítő hatású, mert nehézzé teszi sok esetben a törvények elfogadását a józanész számára, különösen vonatkozik ez a kvantummechanikára és annak részecskefizikai kiterjesztéseire, a kvantumtér elméletekre. Még a fizikusok között is elterjedt az a felfogás, hogy a formalizmust nem érteni kell csak megszokni. Ha a matematikai törvények jól írják le kísérleti megfigyeléseinket, akkor nem fontos, hogy mi az a fizikai tartalom, ami a formulák mögött megbújik. Ebben is tükröződik a modern, iparszerűen űzött tudomány jellegzetessége, amely egyre mélyebbre hatol a részletek megismerésében, eljut a legparányibb fizikai objektumok tulajdonságainak feltárásétól az univerzum, a csillagrendszerek óriásaiig, a legkisebb energiáktól a leghatalmasabb energiák birodalmáig. Ma a specialisták korát éljük, minden tudós ragyogóan érti szűk szakterületének részletkérdéseit, de ugyanakkor egyre kevésbé értjük egymást, egyre jobban halványul a törekvés az NAGY EGÉSZ megismerésére. A fizika olyan mint egy kirakós játék, egy puzzle. Hiába ismerjük a puzzle egyes elemeit a legnagyobb pontossággal, ha az elemeket nem tudjuk jól összeilleszteni, akkor a motívum, a teljes kép nem fog kibontakozni előttünk.
A blog írója is egy a specialisták közül, akinek közel 300 publikációja az elektron mágneses tulajdonságait vizsgálja, ami a részecske egy speciális tulajdonságán, a spinen alapul, de amikor feltettem magamnak a kérdést, hogy mi valójában a spin, zavarba jöttem. Elvben segít a matematika, hiszen a Dirac-egyenlet erre világos definíciót ad, amellett a spin olyan fizikai mennyiség (impulzusmomentum), amivel minden forgást végző test rendelkezik. Mégis a fizika szakkönyvei tartózkodnak annak kijelentésétől, hogy az elektronok és más elemi részecskék sajátforgása (perdülete) hozná létre a spint. Ezt megpróbálják cáfolni is avval, ha a részecske sajátforgásából származna az elektron energiája, tömege és impulzusmomentuma, akkor olyan nagy lenne a forgás sebessége, ami meghaladná a fénysebességet. Engem ezek a magyarázatok nem elégítettek ki, ezért kalandozni kezdtem a fizika különböző területein, és keresni kezdtem a kapcsolatot az egyes területek között, megpróbáltam az elméleteket úgy összeilleszteni, amiből kialakulhat egy átfogó fizika kép, a fizikai valóság. Ennek során jártam végig a speciális és általános relativitáselméletet, a kvantummechanikát és a térelméleteket, a részecskefizika birodalmát. Nem volt célom új matematika formalizmus létrehozása, bár végül erre is akadt példa. hanem összegezni akartam, ellentmondásokat akartam kiküszöbölni és válaszolni néhány homályban maradt kérdésre is.
Szakcikket szakfolyóiratban közölni viszonylag egyszerű, ha az ember betartja a terület szokásos játékszabályait, de komoly nehézséget jelent, ha valaki eltér a bevált sémáktól és új megvilágításba próbálja helyezni a fizika alapkérdéseit. Célom a mérlegre tevés, kritikai észrevételek alapján szeretném látni, hogy helyesek-e megállapításaim. Ennek egyik eszköze ez a blog is, persze nem mondok le arról a lehetőségről sem, hogy szakfolyóiratokban is napvilágot lássanak gondolataim. A blogban emellett közelebb szeretném hozni a fizika világát olyanok számára is, akik nem rendelkeznek magasabb szintű matematikai és fizikai ismeretekkel, ezért néhány bejegyzésben ismeretterjesztő írások is vannak, másutt lábjegyzeteken keresztül kapcsolom össze az ismeretterjesztő szándékot a fizikai precizitással, de vannak olyan bejegyzések is, amelyeket igazán csak a fizikában jártasabbak érthetnek meg.
A legátfogóbb írás a „A részecskefizika nyitott kérései” (technikai okokból két részre bontva). Ennek egy része szakfolyóiratban is megjelent, lásd „A screw model for quantum electrodynamics.: From gravitation to quanta” (szintén két részletben). Egy átfogó fizikai koncepció igényét és a fizika tudományának kritériumait "A modern fizika dilemmái" című bejegyzésben fogalmazom meg. Ehhez kapcsolódnak még a „Fénysebességű forgások és a relativitáselmélet” illetve a "A Dirac-egyenlettől az általános fermion egyenletig című írások, melyekben az egzakt matematikai kifejtés is nyomon követhető. Az előzőeket kiegészíti a "Mi a fény" című bejegyzés is, amely az elektrodinamika hullámegyenleteit veti össze a foton csavarmodelljével, míg "A véges és végtelen az Univerzumban" című írás a fotonok széles spektrumán keresztül vizsgálja a tér és időfelbontás végső határait.. "A kettősforgás csavarpályájának geometriája" írás mutatja be a fermionok sajátmozgásának pályáját. "Az elektron anomális mágneses momentuma" című bejegyzés értelmezi az elektron anomális mágneses moentumát a kéttengelyű fénysebességű forgások segítségével.
Néhány mondatban a legfontosabb megállapítások:
- Az írások kiinduló pontja a speciális relativitáselmélet, amely összhangba hozza a részecskék pontszerűségére vonatkozó megállapításokat a részecskék véges sugarát megkövetelő tulajdonságokkal (spin, azaz impulzusmomentum és a mágneses momentum), ha fénysebességű forgások jönnek létre.
- Azt az erőhatást (erős gravitáció), amely létrehozza a fénysebességű forgásokat az einsteini koncepció alapján magyarázom, aki a tér görbülete és a gravitáció között állapított meg kapcsolatot (általános relativitáselmélet).
- Kifejtem elgondolásaimat a „kettős fizikai világról”, amelyben a téridő görbületei adják meg azt a hátteret, amiben az általunk „látható” részecskék világa megjelenik.
- A két világ kapcsolatát a gyenge kölcsönhatáson keresztül értelmezem és rámutatok a foton és a gyenge kölcsönhatást közvetítő bozonok egyrészt eltérő, de másrészt hasonló tulajdonságaira.
- Fotonok és fermionok (elektron, proton, neutron stb) esetén azonos összefüggést feltételezve az energia és impulzus között (a kettőt a fénysebesség kapcsolja össze), eljutunk a speciális relativitáselmélet törvényeinek ekvivalens megfogalmazásához.
- A Dirac-egyenlet valamennyi fermionra való kiterjesztésével értelmezni lehet a neutrínók és kvarkok szokatlan tulajdonságait (tömeg nélküli neutrínók egymásba alakulása, kvarkok törttöltése és „bezártsága”).
- Fénysebességű forgások hozzák létre az elemi részecskéket és a forgás szimmetriája (kiralitás) határozza meg a részecskék fizikai paramétereit (töltés, tömeg, részecske, antirészecske).
- A kvarkok „szín kvantumszámát” a forgási héjak vibrációi hozzák létre.
A "Térgörbület és gravitáció forgó rendszerekben" című bejegyzésben kiemelten tárgyalom a gravitáció és erős gravitáció kapcsolatát, utalok rá, hogyan kapcsolódik az elképzelés Higgs spontán szimmetriatörési koncepciójához, kitérek kozmológiai kérdésekre és a legkisebb hatás elvére is.
A kvantummechanika ismeretelméleti kérdésivel két írás foglalkozik, az egyik ismeretterjesztő célzatú („Determinizmus és kvantummechanika: a szabadság szintjei a fizikában”), a másik angol nyelvű publikáció az „EPR paradoxon”. Az utóbbi az Einstein, Podolsky és Rosen” által felvetett kérdéssel foglalkozik, amely szerint a kvantummechanikát rejtett paraméterrel kellene bővíteni a determinizmus fenntartása érdekében. A két bejegyzés alapgondolata, hogy a hétköznapi világban kialakított fogalmaink a térről és időről csak korlátozottan alkalmazhatók elemi folyamatok leírására, mert a fogalmainknak azt a valóságot kell tükrözni, ahonnan az információ származik. Mivel a fizikai leírások a szokásos tér és idő fogalmát rávetítik az elemi részecskékre, így szükség van egy matematikai nyelvre, amit kvantummechanikának hívunk, ahol a véletlen és valószínűség bevezetésével lehet áthidalni a két fogalmi rendszer eltérését. A részecskék sajátforgásának fázisa determinisztikussá teszi az elemi folyamatokat, de a fázis ismeretlensége miatt az eredményre csak valószínűségi kijelentések tehetők.
Az "Út a kvantummechanika megértéséhez" c. bejegyzés logikus utat kínál, hogy a klasszikus mechanika fogalmai alapján eljussunk a kvantummechanikai operátorokig. Ebben fontos szerepet játszik a Noether elv. A "Miért diszkrétek az energianívók kötött állapotban?" című öt részes bejegyzés a klasszikus fizika és a kvantummechanika összevetésével elemzi a diszkrét energiaszintek fellépését, amit a foton kvantált tulajdonságára vezet vissza. Az első két rész tárgyalja az oszcillációkat (molekula-vibráció), a további három a bolygómozgás törvényeit veti össze az elektron Bohr modelljével és a Schrödinger egyenlet által adott megoldással..A "Határozatlansági relációk a kvantummechanikában" bejegyzésben a kvantummechanikai inercia erő fogalmát vezetem be, amely biztosítja, hogy a végtelenül nagy Coulomb erő sem tudja befogni az elektront az atommagba. "Az intelligens elektron" című írás (angol nyelven "The intelligent electron") ismeretterjesztő szándékkal - egy megszemélyesített elektronnal folytatott párbeszédben - illusztrálja a makroszkópikus és mikroszkópikus világ eltérő fogalmi rendszerét.
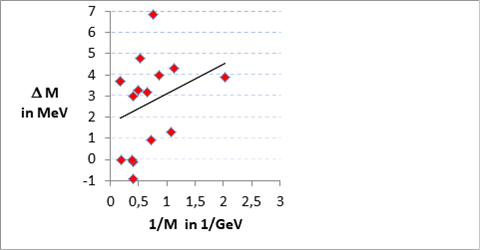
A speciális relativitáselméletben a kinetikus energia és a nyuggalmi energia négyzete adódik össze szemben az energiatagok szokásos összeadási szabályával. Ennek okát vizsgálja meg "The origin of covariance in the special relativity" című írás. Az univerzum gravitációs egyensúlyához több anyagra lenne szükség, mint ami a csillagászati megfigyelésekből következik. Ennek a hiányzó sötét anyagnak az eredetét kívánja tisztázni a "Nyomozás a sötét anyag után" című bejegyzés. Ebben az írásban felvetjük a kérdést, hogy a relativitáselmélettel akkor kapunk összangot, ha a kvarkokból felépülő részecskékben a tömeget (tehát a nyugalmi energiát) négyzetesen adjuk össze a többi energiataggal. Ezt a koncepciót fejleszti tovább a "Barangolás a kvarkok és elemi részecskék világában" című írás, amelyben olyan formulát javasolunk az összetett részecskék tömegére, amelyik nagy pontossággal állítja elő a tömegeket az egyes kvarkok adataiból. Ez segítséget adhat a még nem detektált mezonok és barionok detektálásában is, mert szűkíti a vizsgálandó energiatartományokat.
"Az elektro-gyenge kölcsönhatás és az elemi részecskék átalakulása" három bejegyzés) összehasonlítja az elektromágneses és a gyenge kölcsönhatás legfontosabb mechanizmusait, a fénysebességű csavarmozgás alapján értelmezi a Pauli-féle kizárási elvet valamint a részecskék és anti-részecskék közötti annihilációt, bemutatja a gyenge kölcsönhatás bozonjainak geometriai struktúráját, végül kitér kozmokógiai kérdésekre is az ősrobbanás egy vitatott következményével kapcsolatban. Az írás harmadik része: "A gyenge kölcsönhatás kiválasztási szabályai és a CPT tükrözés" foglalkozik a paritás és a töltéskonjugációval kiegészített paritássértés problémájával a fénysebességű forgásmodell alapján.
A téridő és az elemi részecskék egymást feltételező kapcsolatáról írok a "Téridő-részecske" című bejegyzésben, amelyben szintén felvetem a szokásos tér és idő fogalmak eltérését a mikrovilágban használt fogalmaktól, ami arra vezet a kvantum-elektrodinamikában, hogy megjelennek a formalizmusban a fénynél gyorsabb, sőt időben visszalépő folyamatok is.
Az „Energia, entrópia és evolúció” című bejegyzés ismeretterjesztői szinten kapcsolja össze a három fogalmat. Az evolúciót kiterjeszti az univerzum fejlődésére az ősrobbanástól napjainkig. Az evolúció hajtóereje az univerzum tágulása és az entrópia globális növekedése., amit felgyorsítanak a lokális entrópia csökkenésének szigetei a természetben és az élővilágban.
"Az ősrobbanés és a tertemtésmítoszok" összehasonlítja az ókori mítoszok világát a mai kor ősrobbanás elméletével, amely meglepő párhuzamosságokat is mutat. Javaslatokat teszek ebben az írásban az ősrobbanás elmélet néhány nyitott kérdésére a fénysebességű forgások elvét kivetítva a kezdeti univerzumra. Magyarázatot adok, higy miért domináns az anyag az antianyag felett; és miért nem lehet a gravitációt is kvantumelméleti keretek között leírni.
Az újabb bejegyzések összefoglalását lásd: "Paradigmaváltás a fizikában"
Rockenbauer Antal
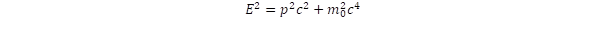
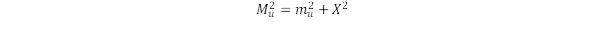
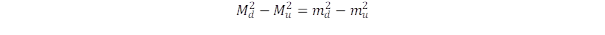
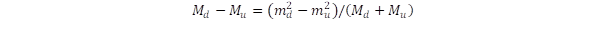
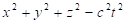 is independent on the choice of inertial frame moving at constant speed [1-2]. A further covariant of the theory is the length of momentum-energy vector (px, py, pz, iE/c), which defines the rest mass by the relation:
is independent on the choice of inertial frame moving at constant speed [1-2]. A further covariant of the theory is the length of momentum-energy vector (px, py, pz, iE/c), which defines the rest mass by the relation: 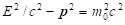 . The energy can be expressed from this relation (1)::
. The energy can be expressed from this relation (1)::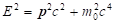
 in the Schroedinger representation, where the linearity of time produces also linear addition rule, thus Eq. (1) can be considered as an exception of the general rule. The question can be raised of why in the special relativity the square of the energy terms is added up? Such relation is expected for orthogonal vectors, namely if the rest energy is produced by an intrinsic momentum and its expectation value is zero <p0> = 0. In this case the total momentum of particles contains an external p1 and intrinsic p0 components:
in the Schroedinger representation, where the linearity of time produces also linear addition rule, thus Eq. (1) can be considered as an exception of the general rule. The question can be raised of why in the special relativity the square of the energy terms is added up? Such relation is expected for orthogonal vectors, namely if the rest energy is produced by an intrinsic momentum and its expectation value is zero <p0> = 0. In this case the total momentum of particles contains an external p1 and intrinsic p0 components: 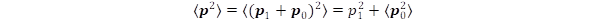 (3)
(3) 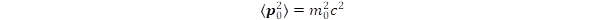 .
.  (4)
(4)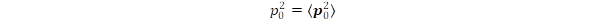
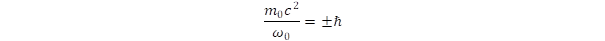
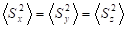 ; which leads to the equation:(5):
; which leads to the equation:(5):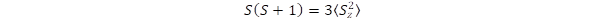 (5)
(5)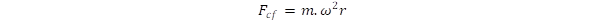
 . As we pointed out in a previous publication [4], this force is balanced by the strong gravitation
. As we pointed out in a previous publication [4], this force is balanced by the strong gravitation caused by the extreme curvature of space, when the rotation has the speed of light. It means that the intrinsic rotation of photons is a self-supporting motion in the space. In the case of double rotations defining the fermions, the strong gravitation has to balance a centrifugal force produced by two different rotations, that is:
caused by the extreme curvature of space, when the rotation has the speed of light. It means that the intrinsic rotation of photons is a self-supporting motion in the space. In the case of double rotations defining the fermions, the strong gravitation has to balance a centrifugal force produced by two different rotations, that is: 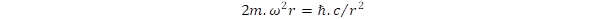 .
. 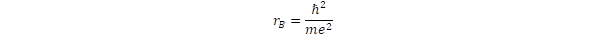

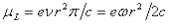

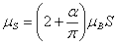
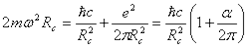
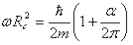
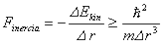


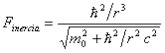
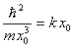 azaz
azaz